Настоящее изобретение относится к области РАДИОЭЛЕКТРОНИКИ, а именно, к способам обработки и обнаружения сигнала на фоне помех. Заявленное изобретение направлено на решение задачи с помощью разработанного оптимального метода обнаружения гидроакустического сигнала в условиях помех, описываемых нелинейными стохастическими дифференциальными уравнениями. Для решения проблемы нелинейности функции в алгоритмах фильтра Калмана-Бьюси предлагается использовать численный метод нелинейной фильтрации [1], [2], [3], [12], известный как сигма-точечный фильтр Калмана (в зарубежной литературе - ансцентный фильтр Калмана) [11], [14].
Задача, на решение которой направлено заявленное изобретение заключается в реализации разработки оптимального метода обнаружения гидроакустического сигнала в условиях помех, описываемых нелинейными стохастическими уравнениями [4], [7], [8], [9], [10]. Поставленная задача решается за счет того, что в заявленном способе аппроксимации подвергается не сама нелинейная функция, а распределение случайной величины. Для этого на каждом этапе алгоритма выбирается оптимальное число сигма-точек, которые затем используются для аппроксимации первых двух моментов случайного процесса [1], [2], [11]. Сигма-точки выбираются оптимальным образом с помощью специального преобразования и с таким расчетом, что бы числовые характеристики(моменты) теоретического распределения были равны соответствующим статистическим характеристикам. Полученные сигма-точки пропускаются через нелинейную функцию состояния, чтобы по ним получить прогнозные значения моментов. Такой подход позволяет обойти проблему нелинейности и реализовать фильтр Калмана для решения задачи фильтрации-обнаружения.
УРОВЕНЬ ТЕХНИКИ - характеризуется наличием наиболее близкого аналога:
- Расширенный фильтр Калмана [2], [3], [13];
Обнаружение сигналов на фоне помехи обуславливается необходимостью расширения задачи фильтрации. Что в свою очередь приводит к разделению задач на два этапа. На первом этапе решается задача фильтрации, которая предполагает нахождение оценки отношения помеха-шум, по критерию минимума среднеквадратичной ошибки. На втором этапе - задача обнаружения, заключающаяся в оценке отношения смеси полезного сигнала и помехи к шуму, по критерию Неймана-Пирсона [8], [9], [10], [13].
Любое оценивание так или иначе связано с нахождением взвешенной суммы априорных и апостериорных данных. Такой подход отражен в уравнениях оценки калмановской фильтрации [13, с. 187]:

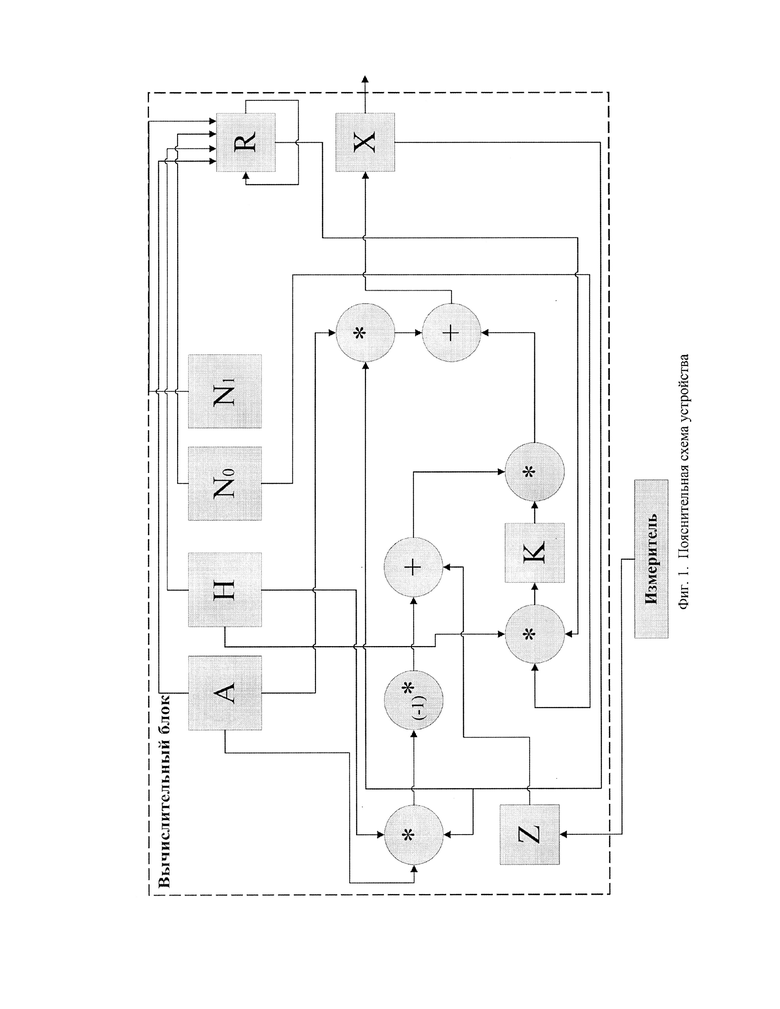
По сути, система уравнений (1) является не абстрактным представлением оценки некоторой безразмерной величины, а как показано на фигуре 1 техническое устройство, реализующее рекуррентный алгоритм, в котором присутствует вычислительной блок дающий прогноз, т.е. априорную информацию и измеритель, предоставляющий апостериорные данные Zk. При этом оценка 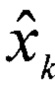 на каждом шаге итерации представляет собой конкретную физическую величину в системе СИ, с соответствующей размерностью. Так, например, для приемника гидроакустических сигналов этой величиной будет являться выходное напряжение
на каждом шаге итерации представляет собой конкретную физическую величину в системе СИ, с соответствующей размерностью. Так, например, для приемника гидроакустических сигналов этой величиной будет являться выходное напряжение 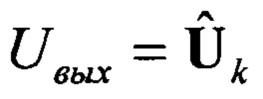 , измеряемое в мВ или мкВ соответственно.
, измеряемое в мВ или мкВ соответственно.
Оптимальное решение задачи оценивания состояния линейной стохастической системы(процесса) по результатам линейных зашумленных наблюдений реализует фильтр Калмана. Однако применение данного алгоритма сопряжено с рядом ограничений, например, возникающих при применении данного алгоритма к нелинейным системам с гауссовскими шумами. Для преодоления данного ограничения в случае нелинейной системы с аддитивными гауссовскими шумами существует ряд методик, из которых, можно выделить те, в основе которых лежит расширенный фильтр Калмана (аналог) [1], [2], [12], [13], являющийся классическим методом применения решения задачи нелинейной фильтрации. Метод расширенного фильтра Калмана базируется на разложении нелинейной функции в правой части стохастического уравнения в ряд Тейлора в окрестности отфильтрованной оценки случайного процесса на каждом шаге алгоритма фильтрации и отсечении всех членов выше первого порядка, таким образом данный алгоритм основан на приближенном сведении исходной нелинейной задачи к линейной. Этот метод фильтрации обеспечивает только первый порядок аппроксимации при оценивании математического ожидания и соответствующей корреляционной матрицы процесса [12].
Пусть уравнения формирования и наблюдения процесса описывается математической моделью, заданной стохастическими дифференциальными уравнениями, [1, с. 87], [13, с. 221]:

Где ƒ,h - нелинейные функции формирования и наблюдения процесса соответственно, n1(t), n0(t) - взаимно независимые векторные шумы с нулевыми математическими ожиданиями и корреляционными матрицами N1, N0 соответственно. Разложим нелинейные функции в уравнениях наблюдения и формирования в функциональный ряд Тейлора в окрестности траектории [10, с. 461] 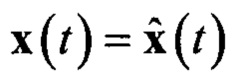 :
:
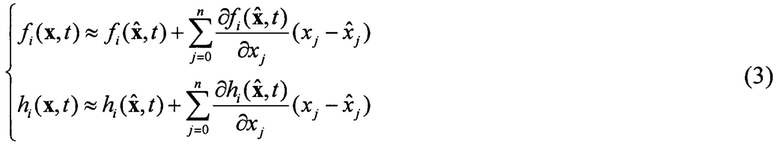
Соответственно уравнения наблюдения и формирования примут вид [10, с. 462]:
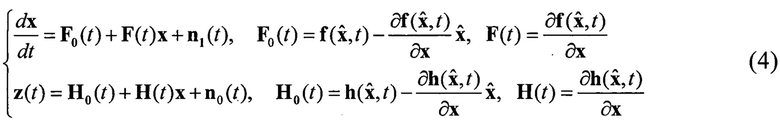
Уравнения (4) линейны относительно х, и следовательно, описывают задачу линейной фильтрации. Входящие в уравнения функции известны, так как они определяются известной по предположению оценкой 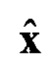 . Поэтому апостериорная плотность вероятности будет нормальной, и, следовательно, остаются в силе уравнения линейной фильтрации [10, с. 462]:
. Поэтому апостериорная плотность вероятности будет нормальной, и, следовательно, остаются в силе уравнения линейной фильтрации [10, с. 462]:
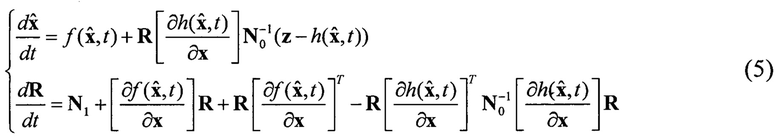
В случае, когда процесс и его измерение заданы дискретно, уравнения формирования и наблюдения могут быть записаны следующим образом:

Система уравнений фильтрации (5) для стохастических уравнений (6) будет иметь вид [1, с. 88]:

Где 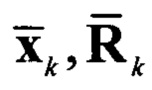 - априорные(прогнозные) значения оценки математического ожидания процесса и корреляционной матрицы ошибки фильтрации.
- априорные(прогнозные) значения оценки математического ожидания процесса и корреляционной матрицы ошибки фильтрации.
В уравнении (7) априорная оценка 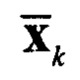 вычисляется интегрированием уравнения
вычисляется интегрированием уравнения 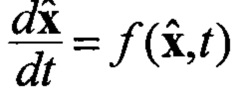 .
.
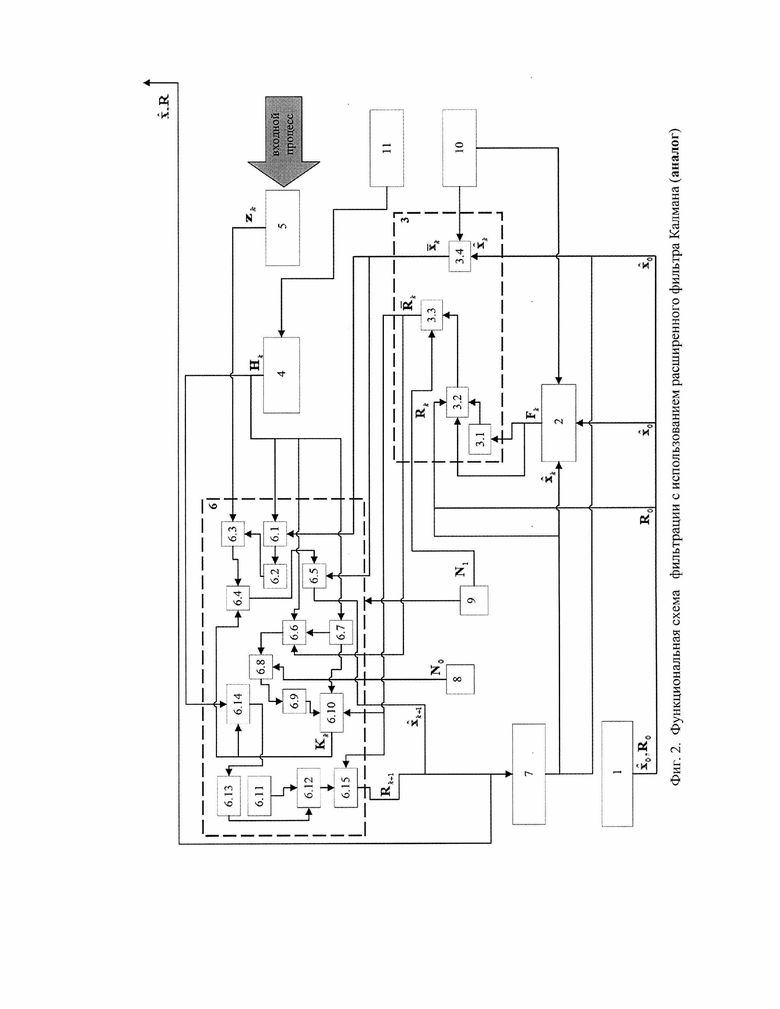
Функциональная схема, реализующая алгоритм расширенного фильтра Калмана представлена на фигуре 2, где
Блок 1 - задание начальных условий 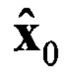 , R0;
, R0;
Блок 2 - вычисление матрицы Якоби Fk, элементы которой представляют собой частные производные вектора формирующей функции;
Блок 3. - вычисление априорных(прогнозируемых) значений оценки 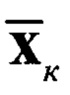 и корреляционной матрицы ошибки фильтрации
и корреляционной матрицы ошибки фильтрации 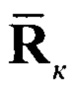 ;
;
Блок 3.1 - блок транспонирования матриц;
Блок 3.2 - умножитель;
Блок 3.3 - сумматор;
Блок 3.4 - интегратор;
Блок 4 - вычисление матрицы Якоби Hk, элементы которой представляют собой частные производные вектора функции наблюдения;
Блок 5 - устройство измерения(наблюдения) процесса zk;
Блок 6 - коррекция прогнозных данных, вычисление текущей оценки 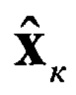 и корреляционной матрицы ошибки фильтрации Rк;
и корреляционной матрицы ошибки фильтрации Rк;
Блоки 6.1, 6.4, 6.6, 6.10, 6.14, 6.15 - блоки умножения матриц;
Блок 6.2, 6.13 - умножитель на коэффициент усиления [-1];
Блоки 6.3, 6.5, 6.8, 6.12 - сумматоры;
Блок 6.7 - блок транспонирования матрицы;
Блок 6.9 - блок преобразования матрицы в обратную;
Блок 6.11 - блок задания единичной матрицы;
Блок 7. - блок задержки k+1;
Блоки 8, 9 - корреляционные матрицы шума наблюдения N0 и формирующего шума N1.
Блок 10 - блок задания формирующей функции процесса;
Блок 11 - блок задания функции наблюдения;
Расширенный фильтр Калмана является широко распространенным и достаточно эффективным рекурсивным вычислительным алгоритмом. Однако его применение и реализация связаны с рядом ограничений [5]. Например, в рамках данного алгоритма предполагается, что линеаризованное преобразование математического ожидания и корреляционной матрицы достаточно близко к заданному нелинейному. Кроме того, требуемая матрица частных производных, получаемая в процессе линеаризации исходной системы, может и не существовать [2], [3].
На современном этапе развития методов нелинейной калмановской фильтрации можно выделить сигма-точечный фильтр Калмана (СТФК)(прототип).
Суть этого алгоритма заключается в том, что на каждом этапе вокруг полученной оценки состояния процесса детерминированным образом выбирают оптимальное (минимальное) число сигма-точек, которые затем используют для аппроксимации первых двух моментов.[1], [2], [3], [12], 14] Сигма-точки выбираются оптимальным образом с помощью специального преобразования и с таким расчетом, чтобы несколько важнейших числовых характеристик (моментов) теоретического распределения были равны соответствующим статистическим характеристикам. В СТФК-методе речь идет о первых двух моментах, т.е. о математическом ожидании и корреляционной матрице неизвестного вектора состояния системы. Затем сигма-точки пропускают через нелинейную функцию правой части дискретного стохастического процесса, чтобы получить прогнозные значения первых двух моментов апостериорного распределения случайной величины. Отметим, что, в отличие от обобщенного фильтра Калмана, в сигма-точечном фильтре Калмана нелинейная функция системы не изменяется, т.е. не линеаризуется. Отсюда вытекает основное преимущество СТФК-фильтра, которое заключается в более высоком порядке аппроксимации оценки математического ожидания случайного процесса 〈x(t)〉 при той же вычислительной сложности, что и в расширенном фильтре Калмана. Доказано, что сигма-точечный фильтр обеспечивает второй порядок аппроксимации, указанной выше величины 〈х(t)〉 для любой достаточно гладкой нелинейной функции формирования процесса. В случае, если функция плотности вероятности состояния системы является симметричной, то СТФК обеспечивает третий порядок аппроксимации (см. доказательство в [14, с. 269]).
Следует отметить, что СТФК-методы развиты для дискретных стохастических динамических систем. Поэтому, чтобы использовать их для оценивания стохастических дифференциальных уравнений, необходимо прежде всего применить тот или иной метод дискретизации и свести задачу к виду, допускающему применение обсуждаемых фильтров. На этом этапе возникает ошибка дискретизации, которая оказывает существенное влияние на работоспособность методов фильтрации.
Пусть случайный процесс x(t) в моменты времени t=t0, t1…ti … описывается следующим уравнением [1]:

где xk - вектор состояния процесса, a ƒ(х) заданная вектор-функция, n1 - дискретный векторный белый шум формирования.
Случайный процесс x(t) в моменты времени t=t0,t1,…ti… доступен по косвенным наблюдениям, удовлетворяющим соотношению:

где zk - вектор дискретных измерений, a n0 - дискретный векторный белый шум наблюдения с нулевым математическим ожиданием и корреляционной матрицей N0.
Требуется в моменты времени t=t0, tl,…ti… no результатам всех имеющихся к этому моменту наблюдений 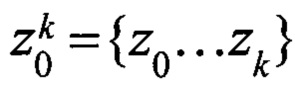 получить вектор оценки состояния системы
получить вектор оценки состояния системы 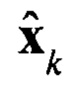 минимизирующую дисперсию ошибки
минимизирующую дисперсию ошибки 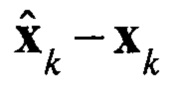 с использованием алгоритма сигма-точечного фильтра Калмана.
с использованием алгоритма сигма-точечного фильтра Калмана.
Далее вводится по определенному правилу набор векторов 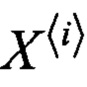 , i=1…k, называемых сигма-точками, таких, что их среднее и корреляционная матрица совпадают с соответствующими моментами случайного процесса х(t). Каждой точке ставится в соответствие некоторой вес
, i=1…k, называемых сигма-точками, таких, что их среднее и корреляционная матрица совпадают с соответствующими моментами случайного процесса х(t). Каждой точке ставится в соответствие некоторой вес 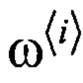 , i=1,…k, таким образом, чтобы обеспечить несмещенную оценку математического ожидания введенного набора частиц, причем:
, i=1,…k, таким образом, чтобы обеспечить несмещенную оценку математического ожидания введенного набора частиц, причем:
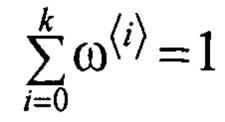
Таким образом сигма-точечный фильтр Калмана оперирует набором точек 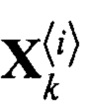 , положения которых определяются заранее заданными соотношениями:
, положения которых определяются заранее заданными соотношениями:
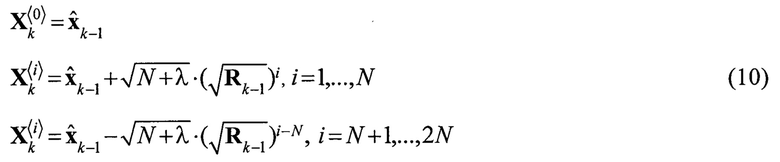
где 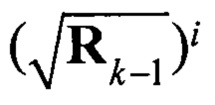 обозначает i-й столбец матрицы
обозначает i-й столбец матрицы 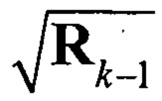 . Здесь используется разложение Холецкого вида
. Здесь используется разложение Холецкого вида 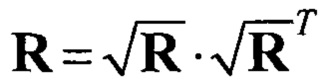 , где
, где 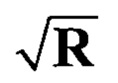 - нижняя треугольная матрица. N - размерность оцениваемого вектора состояния [1], [12], [14].
- нижняя треугольная матрица. N - размерность оцениваемого вектора состояния [1], [12], [14].
Далее заданному нелинейному преобразованию подвергается каждая сигма-точка в отдельности. По преобразованному множеству точек происходит оценивание моментов распределения вектора состояния.
При этом априорная оценка вектора состояния 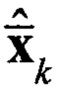 , вычисляется как:
, вычисляется как:

Априорная оценка корреляционной матрицы 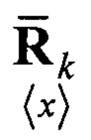 может быть получена по формуле:
может быть получена по формуле:
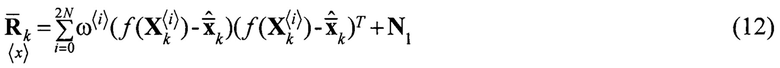
Весовые коэффициенты в формуле (7), (8) и (9) вычисляются как

N1 - корреляционная матрица формирующего шума. При этом весовые коэффициенты в формулах (11) и (12) совпадают, за исключением коэффициента 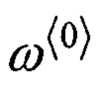 , который в формуле (12) принимает значение:
, который в формуле (12) принимает значение:

Где 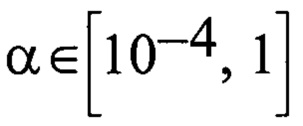 - параметр, определяющий разброс сигма-точек вокруг среднего. Параметр β позволяет учесть априорные данные о функции плотности вероятности неизвестного вектора состояния системы (для нормального распределения β=2). Наконец, λ=α2(N+k)-N - параметр масштабирования. Далее происходит коррекция сделанных на предыдущем этапе оценок вектора процесса и корреляционной матрицы, при помощи модели измерения(наблюдения). Функция наблюдения h(х) из уравнений (9) преобразует сигма-точки (10) в область измерений, где также делается оценка среднего и корреляционной матрицы:
- параметр, определяющий разброс сигма-точек вокруг среднего. Параметр β позволяет учесть априорные данные о функции плотности вероятности неизвестного вектора состояния системы (для нормального распределения β=2). Наконец, λ=α2(N+k)-N - параметр масштабирования. Далее происходит коррекция сделанных на предыдущем этапе оценок вектора процесса и корреляционной матрицы, при помощи модели измерения(наблюдения). Функция наблюдения h(х) из уравнений (9) преобразует сигма-точки (10) в область измерений, где также делается оценка среднего и корреляционной матрицы:
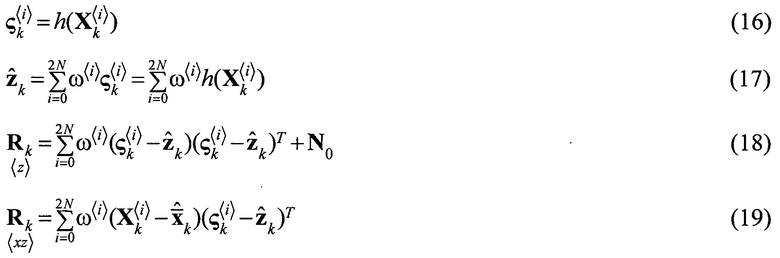
Где
N0 - корреляционная матрица шума наблюдений.
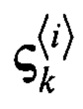 - набор сигма-точек, отображенных в область измерений с помощью функции наблюдения h(•);
- набор сигма-точек, отображенных в область измерений с помощью функции наблюдения h(•);
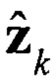 - прогнозная оценка результата измерений на предыдущем шаге.
- прогнозная оценка результата измерений на предыдущем шаге.
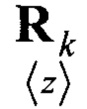 - корреляционная матрица ошибки измерения;
- корреляционная матрица ошибки измерения;
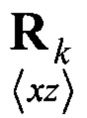 - взаимная корреляционная матрица ошибки фильтрации и измерения;
- взаимная корреляционная матрица ошибки фильтрации и измерения;
Окончательные оценки для вектора процесса и корреляционной матрицы получаются по формулам:

Таким образом, алгоритм сигма-точечного фильтра Калмана имеет три параметра α, β и k, выбор которых определяет конкретную реализацию сигма-точечного фильтра Калмана.
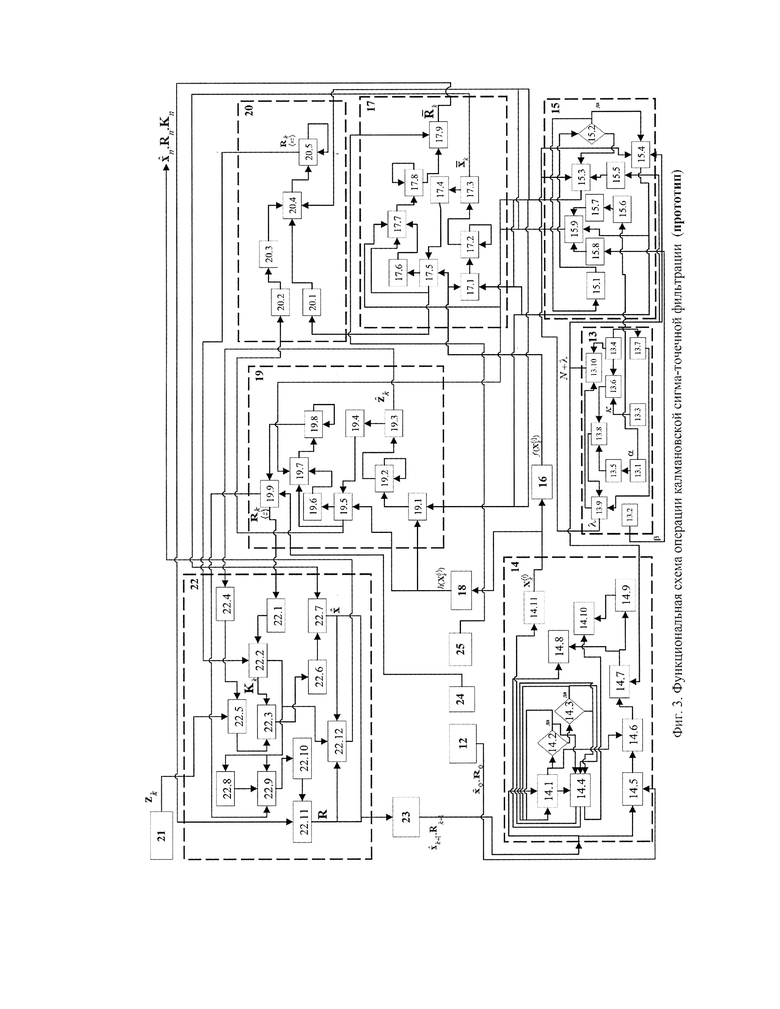
Функциональная схема сигма-точечного фильтра Калмана представлена на фигуре 3, где:
Блок 12 - задание начальных условий 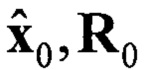 ;
;
Блок 13 - блок вычисления параметра масштабирования λ сигма-точечного фильтра Калмана и параметров α, β и κ, определяющих его конкретную реализацию;
Блоки 13.1, 13.2, 13.3 - блоки задания параметров α, β и κ соответственно;
Блок 13.4 - блок ввода размерности N вектора оценки 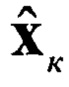 ;
;
Блок 13.5 - блок возведения в квадрат;
Блоки 13.6, 13.9, 13.10 - сумматоры;
Блок 13.7 - блок умножения на коэффициент усиления [-1];
Блок 13.8 - умножитель;
Блок 14. - формирование набора сигма-точек 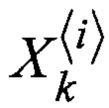 , в соответствии с формулами (10), на вход которого поступает оценка
, в соответствии с формулами (10), на вход которого поступает оценка 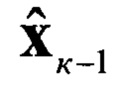 и корреляционная матрица Rк-1 ha предыдущем шаге, где i=0…2N+1, а N - размерность измеряемого вектора;
и корреляционная матрица Rк-1 ha предыдущем шаге, где i=0…2N+1, а N - размерность измеряемого вектора;
Блок 14.1 - блок задания счетчика цикла i=0…2N+1, для формирования необходимого количества сигма-точек 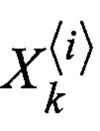 ;
;
Блок 14.2 - блок выполнения проверки условия i=0;
Блок 14.3 - блок выполнения проверки условия 0<i≤N;
Блок 14.3 - блок выполнения проверки условия N<i≤2N;
Блок 14.4 - блок команды считывания входной оценки 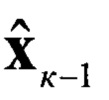 для i-ого шага;
для i-ого шага;
Блок 14.5 - блок вычисления разложения Холецкого для корреляционной матрицы ошибки фильтрации;
Блок 14.6 - блок формирования вектора из i-столбца нижней треугольной матрицы Холецкого;
Блок 14.7 - блок умножения на коэффициент усиления 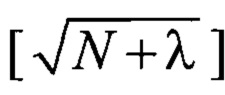 ;
;
Блоки 14.8, 14.10 - сумматоры;
Блок 14.9 - блок умножения на коэффициент усиления [-1];
Блок 14.11 - блок формирования вектора сигма-точек из i значений на k-ом шаге;
Блок 15 - вычисление весовых коэффициентов 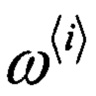 сигма-точечного фильтра по заданным параметрам, по формулам (13), (14) и (15);
сигма-точечного фильтра по заданным параметрам, по формулам (13), (14) и (15);
Блок 15.1 - блок задания счетчика цикла i=0…2N+1, для формирования вектора соответствующих весовых коэффициентов 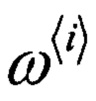 ;
;
Блок 15.2 - блок выполнения проверки условия i=0;
Блоки 15.3, 15.4 - делители;
Блок 15.5 - блок умножения на коэффициент усиления [2];
Блок 15.6 - блок возведения в квадрат;
Блок 15.7 - блок умножения на коэффициент усиления [-1];
Блок 15.8 - блок добавления константы [+1];
Блок 15.9 - сумматор;
Блок 16 - преобразование сигма-точек формирующей функцией 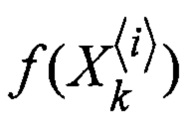 ;
;
Блок 17 - вычисление априорных (прогнозных) значений оценки 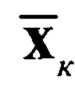 и корреляционной матрицы ошибки фильтрации
и корреляционной матрицы ошибки фильтрации 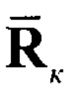 по формулам (11) и (12) соответственно;
по формулам (11) и (12) соответственно;
Блок 17.1 - блок поэлементного перемножения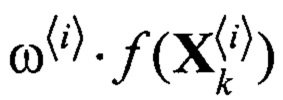 ;
;
Блоки 17.2, 6.8 - накопительные сумматоры;
Блок 17.3 - блок считывания, вычисленной прогнозной оценки 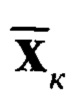 ;
;
Блок 17.4 - блок умножения на коэффициент усиления [-1]
Блоки 17.5, 17.9 - сумматоры
Блок 17.6 - блок транспонирования матриц;
Блок 17.7 - блок поэлементного перемножения 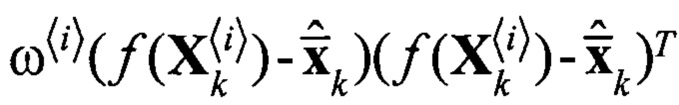 ;
;
Блок 18 - отображение сигма-точек функцией наблюдения в область измерений 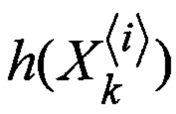 ;
;
Блок 19 - вычисление оценки 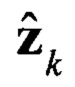 и корреляционной матрицы ошибки измерений
и корреляционной матрицы ошибки измерений 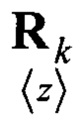 в соответствии с формулами (17), (18);
в соответствии с формулами (17), (18);
Блок 19.1 - блок поэлементного перемножения 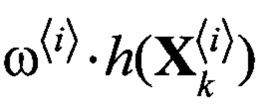 ;
;
Блоки 19.2, 19.8 - накопительные сумматоры;
Блок 19.3 - блок считывания, вычисленной прогнозной оценки 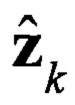 ;
;
Блок 19.4 - блок умножения на коэффициент усиления [-1];
Блоки 19.5, 19.9 - сумматоры;
Блок 19.6 - блок транспонирования матриц;
Блок 19.7 - блок поэлементного перемножения 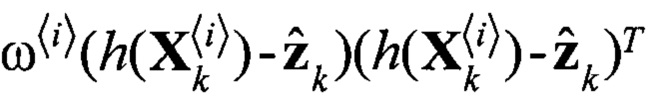 ;
;
Блок 20 - Вычисление взаимной корреляционной матрицы ошибки 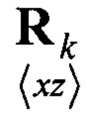 по формуле (19);
по формуле (19);
Блок 20.1 - блок считывания текущего значения 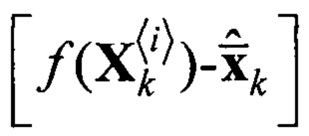 ;
;
Блок 20.2 - блок считывания текущего значения 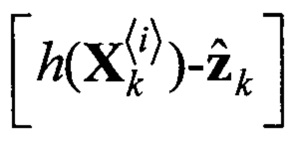 ;
;
Блок 20.3 - блок транспонирования матриц;
Блок 20.4 - блок поэлементного перемножения 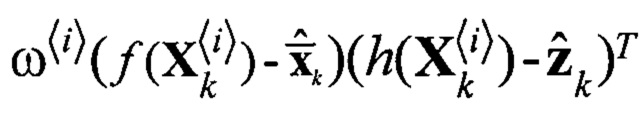 ;
;
Блок 20.5 - накопительный сумматор;
Блок 21 - измеритель, предоставляющий наблюденные данные;
Блок 22 - коррекция прогнозных данных, вычисление текущей оценки 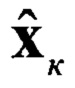 и корреляционной матрицы ошибки фильтрации Rк и коэффициента усиления фильтра Kk;
и корреляционной матрицы ошибки фильтрации Rк и коэффициента усиления фильтра Kk;
Блок 22.1 - блок преобразования матрицы в обратную;
Блок 22.2 - блок перемножения матриц;
Блок 22.3, 22.9 - умножитель;
Блоки 22.4, 22.6, 22.10 - блоки умножения на коэффициент усиления [-1];
Блоки 22.5, 22.7, 22.11 - сумматоры;
Блок 22.8 - блок транспонирования матриц;
Блок 22.12 - блок комплексирования данных;
Блок 23 - блок задержки k+1;
Блоки 24, 25 - корреляционные матрицы шума наблюдения N0 и формирующего шума N1.
Суть изобретения заключается в обобщении задачи фильтрации, с использованием алгоритма сигма-точечного фильтра Калмана до задачи фильтрации-обнаружения:
Для задачи фильтрация-обнаружения сигналов [8, с. 225] можно записать соответствующее линейное стохастическое уравнение, которое описывает помеху х, уравнение наблюдения которого имеет вид [4], [8], [15]:
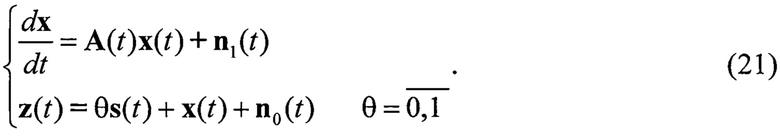
Где θ параметр обнаружения, принимающий значения 1 при наличии сигнала и 0 при его отсутствии.
Известен алгоритм фильтрации помехи, заданной векторно-матричным уравнением (21) и обнаружения сигнала на ее фоне [3 с. 201], [7, с. 90]:
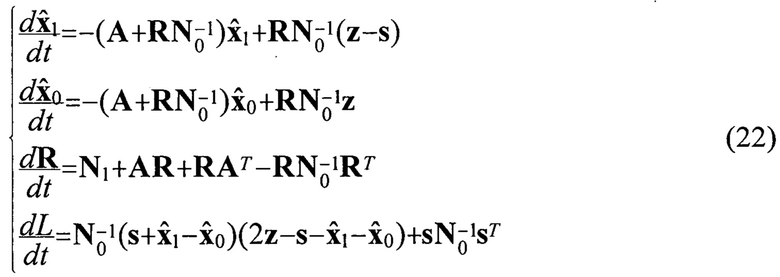
Где:
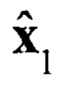 Оценка помехи при наличии сигнала;
Оценка помехи при наличии сигнала;
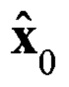 Оценка помехи при отсутствии сигнала;
Оценка помехи при отсутствии сигнала;
z Входная реализация;
s Детерминированный сигнал;
N1, N0 Соответствующие матрицы спектральных плотностей аддитивных шумов n1(t), n0(t);
R Корреляционная матрица ошибок фильтрации;
L Эволюция отношения правдоподобия;
А Матрица формирующих функций;
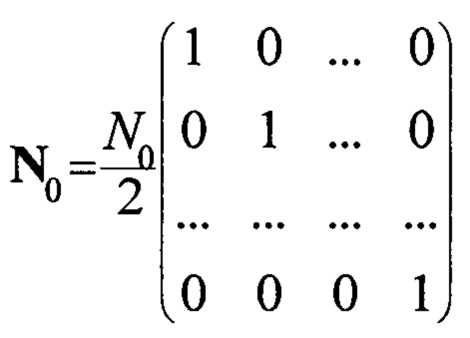
В общем случае уравнение наблюдения, описываемое системой нелинейных стохастических дифференциальных уравнений, имеет вид:
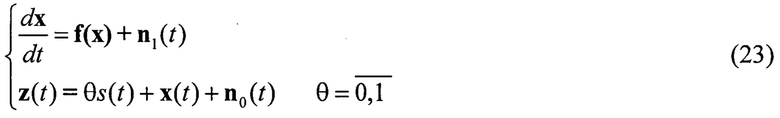
Перепишем систему уравнений (23) в дискретном виде:

Уравнения калмановской фильтрации, соответствующие системе (24) при условии линейности ƒ(xk)=Akxk и 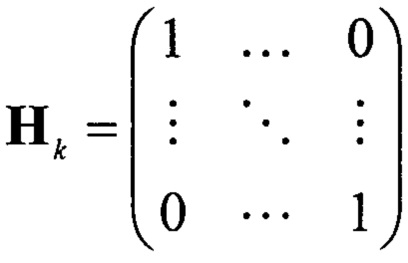 будут иметь вид:
будут иметь вид:
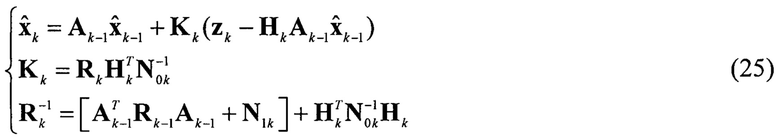
Основная сложность при реализации алгоритма (25) связана с большим вычислением, требуемым для обращения матрицы в третьем уравнении. Более простой является модификация алгоритма, основанная на использовании леммы об обращении матриц [13, с. 192].
Модифицированный алгоритм будет выглядеть следующим образом:
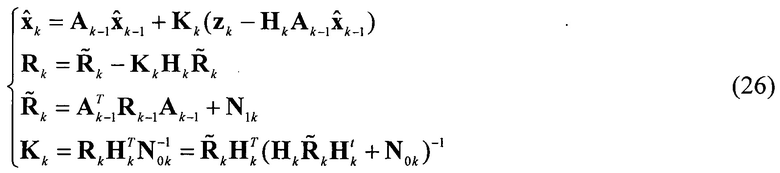
Где корреляционная матрица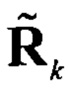 полученная алгебраическим путем, и введенная для упрощения записи уравнений (25), представляет собой ни что иное как априорную матрицу корреляции
полученная алгебраическим путем, и введенная для упрощения записи уравнений (25), представляет собой ни что иное как априорную матрицу корреляции 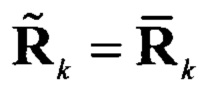 из СДУ (7), (20).
из СДУ (7), (20).
Алгоритм фильтрации, записанный в форме (26) позволяет увидеть умозрительную связь с алгоритмом СТФК (20), при условии линейности ƒ(xk)=Axk и h(xk)=Hkxk, 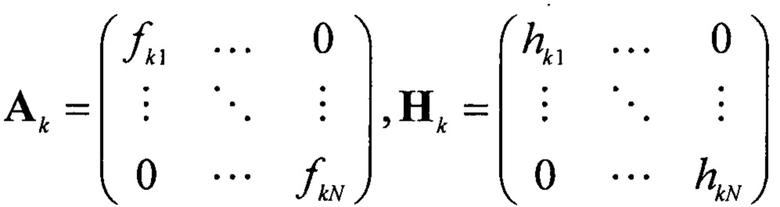
Применяя алгоритм, сигма-точечного фильтра Калмана к системе (24), получим уравнения фильтрации, по аналогии с системой (25), с той разницей, что функции ƒ(xk), h(xk)являются уже нелинейными:
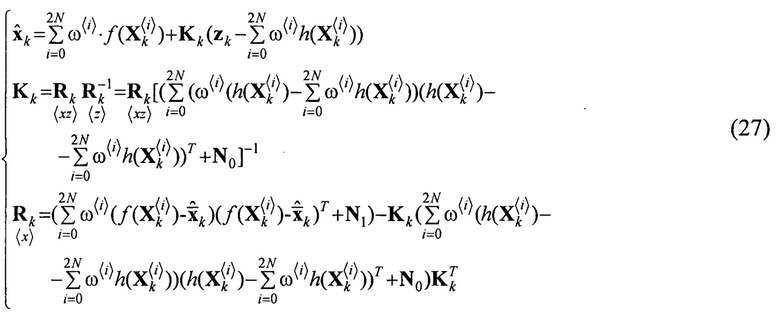
Перепишем систему (24) в следующем виде:
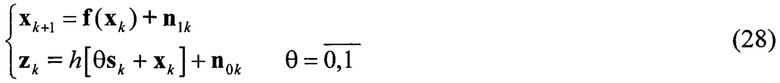
К системе (28) можно применить уравнения фильтрации-обнаружения (22), с учетом алгоритма сигма-точечного фильтра Калмана(прототип) (27). С этой целью вышеуказанный алгоритм для каждой из гипотез наличия сигнала во входной реализации (θ=1) и отсутствия сигнала (θ=0) приведет к появлению дополнительных уравнений. С учетом h(xk)=Hkxk уравнения примут вид:
 Где:
Где:
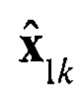 - оценка помехи, при гипотезе наличия сигнала;
- оценка помехи, при гипотезе наличия сигнала;
 - оценка поме5хи при гипотезе отсутствия сигнала;
- оценка поме5хи при гипотезе отсутствия сигнала;
Kk1 - коэффициент усиления фильтра при гипотезе наличия сигнала;
Kk0 - коэффициент усиления фильтра при гипотезе отсутствия сигнала;
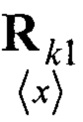 - корреляционная матрица ошибки фильтрации при гипотезе наличия сигнала;
- корреляционная матрица ошибки фильтрации при гипотезе наличия сигнала;
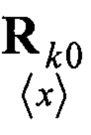 - корреляционная матрица ошибки фильтрации при гипотезе отсутствия сигнала;
- корреляционная матрица ошибки фильтрации при гипотезе отсутствия сигнала;
Lk - эволюция отношения правдоподобия;
zk - входная реализация, размерности N, содержащая либо смесь помехи и сигнала, либо помеху;
sk - реализация сигнала, размерности N
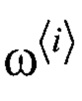 - весовые коэффициенты, где i=0…2N;
- весовые коэффициенты, где i=0…2N;
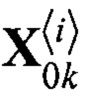 - набор из i-сигма-точек при гипотезе отсутствия сигнала, где i=0…2N;
- набор из i-сигма-точек при гипотезе отсутствия сигнала, где i=0…2N;
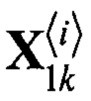 - набор из i-сигма-точек при гипотезе наличия сигнала, где i=0...2N;
- набор из i-сигма-точек при гипотезе наличия сигнала, где i=0...2N;
Hk - матрица функций наблюдения;
ƒ(•) - матрица формирующих функций;
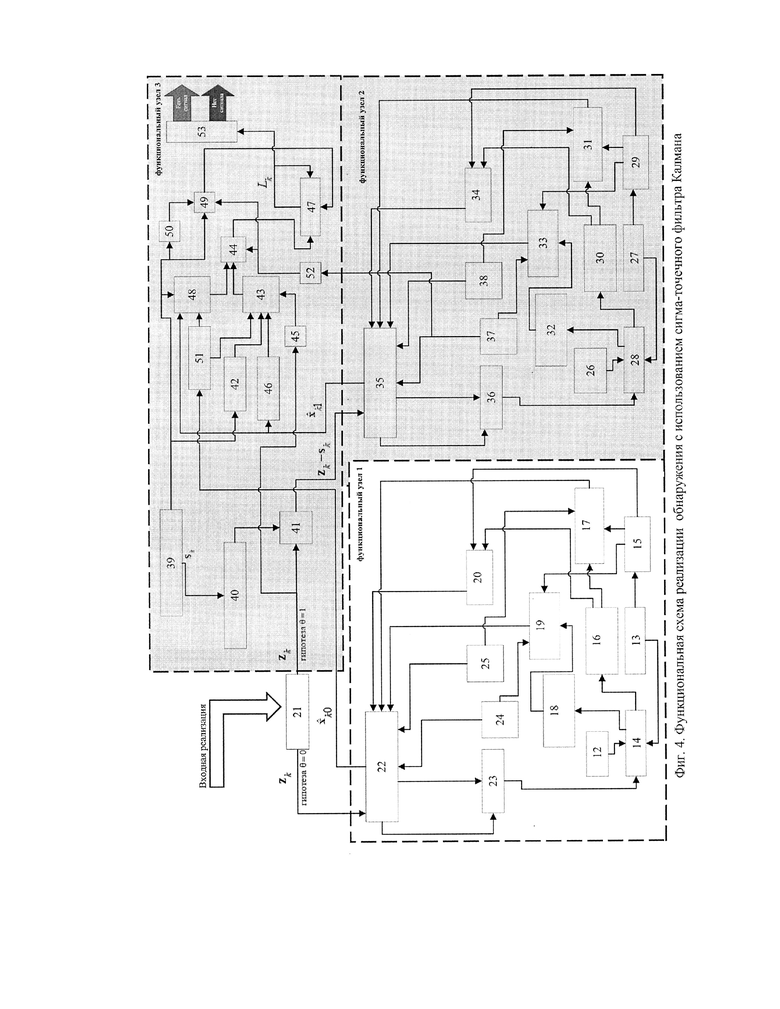
Схема, реализации алгоритма (29) фильтрации-обнаружения с использованием сигма-точечного фильтра Калмана представлена на фигуре 4, где:
Блоки 12-25 - алгоритм сигма-точечного фильтра Калмана, в соответствии с функциональной схемой фигуры 3;
Блоки 12, 26 - задание начальных условий 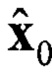 , R0;
, R0;
Блоки 13, 27 - задание параметров сигма-точечного фильтра Калмана α, β и k, определяющих его конкретную реализацию;
Блоки 14, 28 - формирование набора сигма-точек 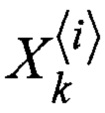 , в соответствии с формулами (7), где N - размерность измеряемого вектора, а i=0…2N+1;
, в соответствии с формулами (7), где N - размерность измеряемого вектора, а i=0…2N+1;
Блоки 15, 29 - вычисление весовых коэффициентов 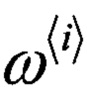 сигма-точечного фильтра по заданным параметрам, по формулам (10), (11) и (12);
сигма-точечного фильтра по заданным параметрам, по формулам (10), (11) и (12);
Блоки 16, 30 - преобразование сигма-точек формирующей функцией 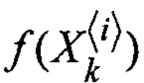
Блоки 17,31 - вычисление априорных (прогнозных) значений оценки 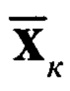 и корреляционной матрицы ошибки фильтрации
и корреляционной матрицы ошибки фильтрации  по формулам (11) и (12) соответственно;
по формулам (11) и (12) соответственно;
Блоки 18, 32 - отображение сигма-точек функцией наблюдения в пространство измерений 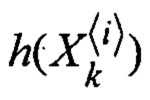 ;
;
Блоки 19, 33 - вычисление оценки  и корреляционной матрицы ошибки измерений
и корреляционной матрицы ошибки измерений  в соответствии с формулами (17), (18);
в соответствии с формулами (17), (18);
Блоки 20, 34 - вычисление взаимной корреляционной матрицы ошибки 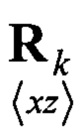 по формуле (19);
по формуле (19);
Блок 21 - измеритель, предоставляющий наблюденные данные;
Блоки 22, 35 - коррекция прогнозных данных, вычисление текущей оценки 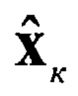 корреляционной матрицы ошибки фильтрации Rк и коэффициента усиления фильтра Kk;
корреляционной матрицы ошибки фильтрации Rк и коэффициента усиления фильтра Kk;
Блоки 23, 36 - блок задержки k+1;
Блоки 24, 37 и 25, 38 - корреляционные матрицы шума наблюдения N0 и формирующего шума N1 соответственно;
Блок 39 - Задание дискретной последовательности векторов эталонного сигнала;
Блок 40, 42, 46, 51 - умножитель на коэффициент усиления [-1];
Блоки 41, 43, 47, 48 - сумматоры;
Блоки 44, 49 - умножители;
Блок 45 - умножитель на коэффициент усиления [2];
Блок 50 - блок транспонирования матрицы;
Блок 52 - блок преобразования матрицы в обратную;
Блок 53 - пороговое устройство;
Блоки 12-20, 22-25 - объединены в функциональный узел 1 реализующий алгоритм сигма-точечного фильтра Калмана, в соответствии с функциональной схемой фигуры 3 при гипотезе отсутствия сигнала (θ=0);
Блоки 26-41 - объединены в функциональный узел 2 реализующий алгоритм сигма-точечного фильтра Калмана, в соответствии с функциональной схемой фигуры 3 при гипотезе наличия сигнала (θ=1) во входной реализации;
Блоки 42-53 - объединены в функциональный узел 3 реализующий операцию решения уравнения эволюции отношения правдоподобия, в соответствии с седьмым уравнением системы (29);
Как показано на фигуре 4, идея изобретения заключается в добавлении к функциональным узлам 2 и 3 к функциональному узлу 1 (прототип). При этом функциональный узел 2, по сути, копирует прототип, решая при этом задачу фильтрации помехи для гипотезы наличия сигнала. А функциональный узел 3 является устройством, по результатам вычисления которого выносится решение об обнаружении или не обнаружении сигнала.
Иначе изобретение можно интерпретировать как добавление функционального узла 3 к функциональным узлам 1, 2 фигуры 4, решающим задачи фильтрации с помощью сигма-точечного фильтра Калмана для противоположных гипотез наличия или отсутствия сигнала.
К описанию прилагаются четыре чертежа:
Фигура 1 - Пояснительная схема устройства.
Фигура 2 - Аналог. Функциональная схема фильтрации с использованием расширенного фильтра Калмана.
Фигура 3 - Прототип. Функциональная операция калмановской сигма-точечной фильтрации.
Фигура 4 - Предлагаемый способ. Функциональная схема реализации обнаружения с использованием сигма-точечного фильтра Калмана.
Список использованных источников
1. Шавин М.Ю. Численные методы нелинейной фильтрации для оценки состояния квадрокоптера с поворотными роторами. ТРУДЫ МФТИ. 2019. Том 11, №3
2. Куликова М.В., Куликов Г.Ю. Численные методы нелинейной фильтрации для обработки сигналов и измерений. Центр прикладной математики, Высший технический институт, Университет г. Лиссабона, Португалия, Вычислительные технологии, Том 21, №4, 2016.
3. Кудрявцева И.А. Анализ эффективности расширенного фильтра Калмана, сигма-точечного фильтра Калмана и сигма-точечного фильтра частиц. Научный вестник МГТУ. Том 19, №2, 2016.
4. Бутырский Е.Ю. Обнаружение сигналов на фоне марковской реверберационной помехи // Научное приборостроение, Т. 22, №3, 2012. С.87-95.
5. Ашинянц Р.А., Морозова Т.Ю. Регуляризация алгоритма фильтрации Калмана-Бьюси при плохой обусловленности корреляционной матрицы шума // Цифровая обработка сигналов, №4, 2007. С. 29-32.
6. Розов А.К. Нелинейная фильтрация сигналов. Санкт-Петербург: Политехника, 1994. 381 с.
7. Бутырский Е.Ю. Обнаружение сигналов на фоне марковской реверберационной помехи // Научное приборостроение, Т. 22, №1, 2012. С. 87-95.
8. Сосулин Ю.Г. Теория обнаружения и оценивания стохастических сигналов. Москва: Советское радио, 1978. 319 с.
9. Казаков В.А. Введение в теорию марковских процессов и некоторые радиотехнические задачи. Москва: Советское радио, 1973. 232 с.
10. Тихонов В.И., Харрисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. Москва: Радио и связь, 1991. 608 с.
11. Eric A. Wan and Rudolph van der Merwe. The Unscented Kalman Filter for Nonlinear Estimation. Oregon Graduate Institute of Science & Technology 20000 NW Walker Rd, Beaverton, Oregon 97006 ericwan@ece.ogi.edu, rvdmerwe@ece.ogi.edu.
12. Кудрявцева И.А., Волков B.A. Численное решение задач нелинейной фильтрации на основе алгоритмов фильтра частиц. Труды МАИ. Выпуск №89.
13. Бутырский Е.Ю. Методы моделирования и оценивания случайных величин и процессов. СПб: Стратегия Будущего, 2020. 642 с.
14. Wan, Е.А., van der Merwe, R. The unscented Kalman filter. Chapter 7: Kalman filtering and neural networks / Ed. S. Haykin. N. Y.: John Wiley & Sons, 2001. P. 221-280.
15. Бутырский Е.Ю. Панкратова К.И. Методы обнаружения широкополосных сигналов // материалы XI международной научно-практической конференции, секция технические науки, 2015. С. 4-18.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБРАБОТКИ СИГНАЛОВ | 2022 |
|
RU2801897C1 |
| СПОСОБ ОБРАБОТКИ СИГНАЛОВ | 2021 |
|
RU2782160C1 |
| Способ сплайн-фильтрации сигналов | 2017 |
|
RU2651640C1 |
| РОБАСТНЫЙ СТОХАСТИЧЕСКИЙ ФИЛЬТР | 2024 |
|
RU2826922C1 |
| УСТРОЙСТВО АДАПТИВНОГО ОЦЕНИВАНИЯ СОСРЕДОТОЧЕННОЙ ПОМЕХИ | 2008 |
|
RU2381620C1 |
| Робастный стохастический фильтр | 2021 |
|
RU2755677C1 |
| СПОСОБ ОЦЕНКИ НАВИГАЦИОННОГО СОСТОЯНИЯ В УСЛОВИЯХ ОГРАНИЧЕННОЙ ВОЗМОЖНОСТИ НАБЛЮДЕНИЯ | 2015 |
|
RU2701194C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ И ПАРАМЕТРОВ ДВИЖЕНИЯ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЙ ПО ИЗМЕРЕНИЯМ ИХ НЕСУЩЕЙ ЧАСТОТЫ | 2021 |
|
RU2776078C1 |
| Робастный дискретный стохастический фильтр | 2023 |
|
RU2804256C1 |
| СПОСОБ И СИСТЕМА ОЦЕНКИ РАСХОДА ТЕКУЧЕЙ СРЕДЫ | 2015 |
|
RU2690080C2 |
Использование: для обработки сигнала при наличии помех в области радиоэлектроники и гидроакустики. Сущность изобретения заключается в том, что применяется алгоритм сигма-точечного фильтра Калмана, при этом уравнения фильтрации разбиваются на уравнение оценки состояния при гипотезе наличия сигнала, уравнения оценки дисперсии ошибки фильтрации для каждой гипотезы и соответствующие уравнения для коэффициентов усиления фильтра. Кроме того, дополнительно решается уравнение правдоподобия, включающее эти оценки, по результатам вычисления которого выносится решение об обнаружении или не обнаружении сигнала. Технический результат: обеспечение возможности уменьшения вычислительных операций, а также обеспечение возможности использования алгоритма фильтрации, позволяющего надежным образом обнаружить сигнал при различных помехах в реальном масштабе времени. 4 ил.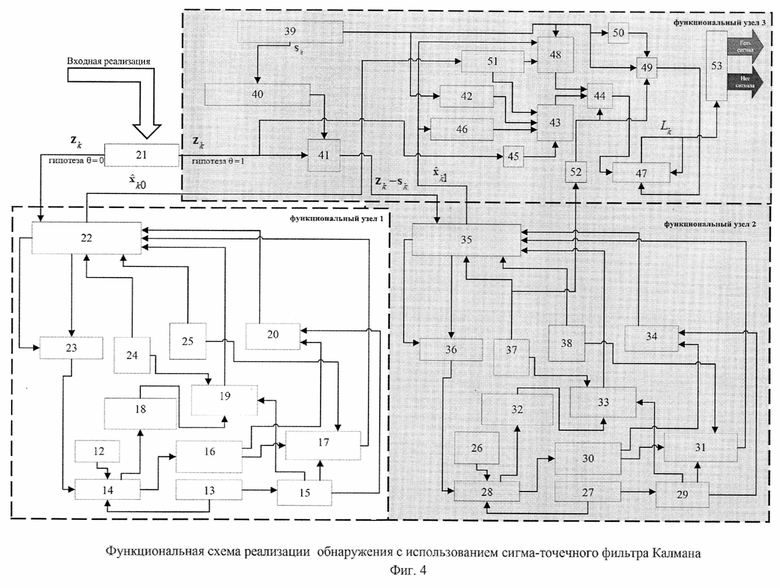
Способ обработки сигналов с использованием алгоритма сигма-точечного фильтра Калмана, основанный на сигма-точечной калмановской фильтрации, включающий последовательность операций, а именно: операцию, реализующую сигма-точечное преобразование, заключающееся в формировании необходимого количества сигма-точек из оценок помехи и дисперсии ошибки фильтрации предыдущего шага, взвешенная сумма которых позволяет выполнять нелинейные преобразования без искажений вероятностных характеристик; операцию преобразования сигма-точек с помощью формирующей функции и функции наблюдения; операцию решения уравнения дисперсии ошибки фильтрации и операцию решения уравнения для вычисления коэффициентов усиления фильтра с помощью преобразованных сигма-точек; операцию решения уравнения калмановской фильтрации в дискретном виде для получения несмещенной взвешенной оценки помехи с использованием образов полученных сигма-точек с целью получения оценок помехи при нелинейном уравнении состояния и уменьшения вычислительных затрат при нелинейной фильтрации, отличающийся тем, что с целью решения задачи обнаружения сигнала из измеренных значений физической смеси сигнала, марковской помехи и белого шума, поступающих на вход системы обработки, дополнительно на каждом шаге вместо одной выполняется две операции решения уравнений фильтрации смеси сигнала и помехи, использующие алгоритм сигма-точечного фильтра Калмана, для гипотез наличия и отсутствия сигнала соответственно и операцию получения отношения правдоподобия, включающего эти оценки и по результатам вычисления которого выполняется операция принятия решения об обнаружении или не обнаружении сигнала в принимаемой физической смеси сигнала и помехи, поступающей на вход системы обработки.
| М.В | |||
| Куликова, Г.Ю | |||
| Куликов, Численные методы нелинейной фильтрации для обработки сигналов и измерений, Вычислительные технологии, Том 21, N 4, 2016, с | |||
| Нефтяной конвертер | 1922 |
|
SU64A1 |
| УСТРОЙСТВО И СПОСОБ ТРЕХМЕРНОГО ПОЗИЦИОНИРОВАНИЯ | 2011 |
|
RU2510046C2 |
| US 2011264392 A1, 27.10.2011 | |||
| CN 109388778 A, 26.02.2019 | |||
| US 2011301436 A1, 08.12.2011. | |||
Авторы
Даты
2025-05-16—Публикация
2024-05-03—Подача