Код с малой плотностью проверок на чётность (low density parity check – LDPC) обычно задаётся своей проверочной матрицей H размерностью M×N, которая обладает свойством разреженности, т.е. её строки и столбцы содержат мало ненулевых позиций по сравнению с размерностью матрицы. LDPC код может быть представлен с помощью графа Таннера {V,E}, который является двудольным неориентированным графом, содержащим V=M+N – вершин (N – символьных и M - проверочных), и E – рёбер, соединяющих вершины графа, соответствуют ненулевым позициям в проверочной матрице. Стоит отметить, что LDPC, как и любой другой линейный блоковый код, может быть описан с помощью порождающей матрицы G, которая в общем случае не является разреженной и обычно используется в процедуре кодирования. Различные способы представления низкоплотностного кода приведены на фиг. 1.
Все коды с малой плотностью проверок на чётность можно разделить на регулярные и нерегулярные. Код называется (ds,dc)-регулярным, если каждый столбец и каждая строка его проверочной матрицы содержит ds и dc ненулевых элементов соответственно. При этом кодовая скорость определяется по формуле:
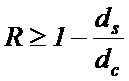 .
.
В противном случае код является нерегулярным и описывается с помощью весовых многочленов степеней символьных и проверочных вершин λ(x) и ρ(x), аналитические выражения которых имеют вид:
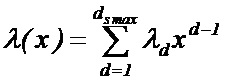 ,
, 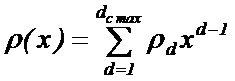
где λd/ρd – доля столбцов/строк проверочной матрицы, имеющих вес d, ds max и dc max – максимальный вес столбцов и строк соответственно. Введя обозначения
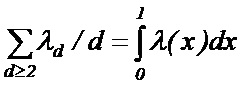 ,
,
несложно показать, что для нерегулярного LDPC кода кодовая скорость может быть вычислена по следующей формуле:
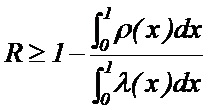 .
.
Было обнаружено, что эффективность нерегулярных LDPC конструкций превосходит регулярные в случае оптимизации весовых многочленов с использованием ряда критериев и статических характеристик канала. Существует несколько методов оптимизации, дающих асимптотически хорошие результаты.
Существующие классы низкоплотностных кодов могут быть разделены на псевдослучайные, основанные на оптимизации весовых распределений λ(x), ρ(x) и алгоритмах компьютерного моделирования, и детерминированные, использующие свойства тех объектов, на базе которых они построены.
Основными характеристиками LDPC кодов являются – минимальное кодовое расстояние (d0) и величина цикла минимальной длины либо обхват графа Таннера (g0). Для классических линейных блоковых кодов параметр d0 непосредственно связан с числом гарантированно исправляемых ошибок, однако низкоплотностные коды при использовании итеративного алгоритма декодирования показывают результаты близкие к пределу Шеннона при малом значении d0. В работе Р. Галлагера было показано, что для ансамбля регулярных LDPC кодов величина минимального кодового расстояния зависит от параметра N линейно. Позднее Таннер обнаружил, что для низкоплотностных кодов с весом столбцов ds = 2 существует детерминированная связь между параметрами g0 и d0:
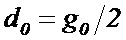 ,
,
при которой зависимость d0(N) становится логарифмической, что негативно сказывается на энергетической эффективности таких кодовых конструкций.
Наличие коротких циклов, в особенности длиной 4 (фиг. 1), в графе Таннера приводит к уменьшению статической независимости итераций декодера, что отрицательно сказывается на помехоустойчивости LDPC кода. В работе было показано, что число независимых итераций T зависит от обхвата графа и ограничено условиями следующего неравенства:
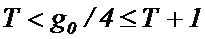 .
.
Однако для увеличения обхвата графа Таннера необходимо либо увеличивать параметр N, либо уменьшать плотность заполнения ненулевыми элементами проверочной матрицы, что значительно уменьшит энергетическую эффективность системы кодирования при минимально возможном ds = 2.
Процедура кодирования линейных блоковых кодов, в том числе и LDPC, в общем случае выполняется в систематической форме и сводится к нахождению проверочной части кодового слова при помощи порождающей матрицы G:
 ,
, ,
,
где K – число бит в информационном слове, u и c – информационный и кодовый вектора соответственно.
В тоже время коды с низкой плотностью проверок на чётность чаще задаются своей проверочной матрицей, поэтому целесообразно рассмотреть её применение в процедуре кодирования. Известно, что любое кодовое слово удовлетворяет следующему выражению:
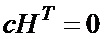 .
.
Пусть проверочная матрица имеет полный ранг, тогда в результате разложения по алгоритму Жордана-Гаусса её можно представить состоящей из двух частей – обратимой матрицы Hp размерностью 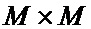 , и необратимой Hs размерностью
, и необратимой Hs размерностью 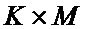 :
:
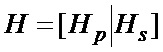
Представив кодовый вектор с в систематической форме c=[cp cs], получим выражение:
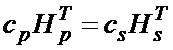 .
.
Согласно (10) проверочные биты вычисляются следующим образом:
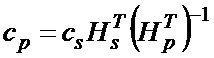 .
.
Сложность рассмотренной процедуры кодирования определяется вычислительными затратами алгоритма Жордана-Гаусса, как O(N3), который выполняется всего один раз на этапе предобработки, а также числом математических операций необходимых для получения проверочных бит согласно выражению (11) равным O(N2). Стоит отметить, что существуют LDPC коды, сложность кодирования для которых находится в линейной зависимости от длины.
Существуют многочисленные классы LDPC кодов, некоторые из которых обладают особой структурой, позволяющие реализовать вычислительно эффективные алгоритмы кодирования. Нерегулярный код повторения-накопления (IRA-irregular repeat accumulate), который представлен на фиг. 2, является одним из них.
Проверочная матрица IRA кода состоит из двух частей – разреженной матрицы перестановок Hs размерностью  и ступенчатой матрицы Hp размерностью
и ступенчатой матрицы Hp размерностью 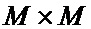 . Такая структура кода позволяет без особого труда получить порождающую матрицу вида:
. Такая структура кода позволяет без особого труда получить порождающую матрицу вида:
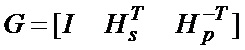 ,
,
с помощью которой обычно выполняется процедура кодирования. Стоит отметить, что матрица 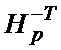 является верхней треугольной:
является верхней треугольной:
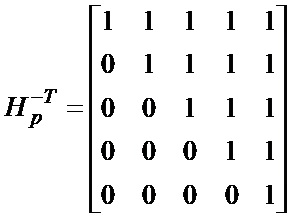 .
.
Не трудно показать, что операция умножения информационного вектора на матрицу 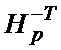 эквивалентна накоплению результата в простейшем аккумуляторе.
эквивалентна накоплению результата в простейшем аккумуляторе.
В соответствии с формулой (12) получение порождающей матрицы не обязательно, т.к. все необходимые для процедуры кодирования вычисления могут быть реализованы в соответствии со схемой кодера, представленной на фиг. 3, по проверочной матрице.
Основные вычислительные затраты в случае кодирования IRA кодов приходятся на матричный умножитель, но разреженность матрицы Hs позволяет достичь линейной сложности кодирования.
Малое количество ненулевых элементов в проверочной матрице LDPC кода потенциально позволяет снизить сложность процедуры кодирования до линейной. Используя операции перестановок строк и столбцов в матрице произвольной формы, было предложено преобразовать исходную проверочную матрицу к форме, изображённой на фиг. 4.
В этом случае матрица T должна быть квадратной и верхней треугольной. Свойство разреженности LDPC кода после выполнения триангуляции (преобразование H в H’) сохраняется. Вычислительные затраты на кодирование в случае разложения вида (фиг. 4) могут определяться, как O(N) при g=0 либо, как O(N+g2), g≠0. Поэтому цель алгоритма состоит в определении такого способа разложения матрицы H в H’, при котором минимизируется параметр g. Фактически процедура кодирования заключается в определении проверочных бит по информационным. Рассматривая уравнение HcT=0, домножим его на матрицу 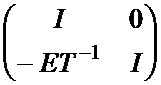 справа и получим:
справа и получим:
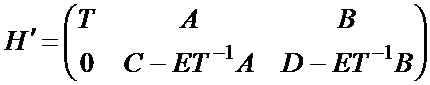 .
.
Выполнив, таким образом, первую часть разложения Жордана – Гаусса, представим кодовый вектор в виде 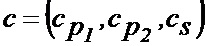 , причём длины векторов
, причём длины векторов 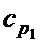 и
и 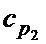 равны (N-K-g) и g соответственно. Для нахождения проверочной части кодового слова рассмотрим систему уравнений:
равны (N-K-g) и g соответственно. Для нахождения проверочной части кодового слова рассмотрим систему уравнений:
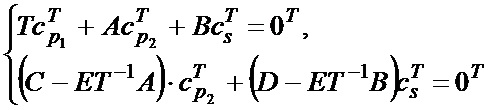 .
.
Вводя замену вида 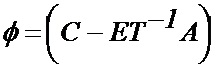 , получим искомые выражения для вычисления проверочных бит:
, получим искомые выражения для вычисления проверочных бит:
 .
.
Для уменьшения вычислительных затрат процедуру кодирования следует разбить на две стадии, а именно предобработка и определение векторов 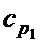 и
и 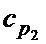 . На этапе предобработки благодаря перестановкам строк и столбцов проверочная матрица преобразуется к виду
. На этапе предобработки благодаря перестановкам строк и столбцов проверочная матрица преобразуется к виду 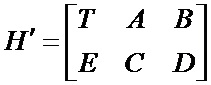 . После чего выполняется проверка матрицы
. После чего выполняется проверка матрицы 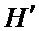 на не вырожденность путём обращения матрицы
на не вырожденность путём обращения матрицы 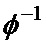 . В случае успешного выполнения проверки переходим к этапу кодирования, в результате которого вычислим по формуле (16) проверочные вектора.
. В случае успешного выполнения проверки переходим к этапу кодирования, в результате которого вычислим по формуле (16) проверочные вектора.
Изобретение относится к системам телекоммуникаций и эфирным видеоинформационным системам вещания и может найти применение в кодерах устройств передачи дискретной информации.
Известен способ обработки данных с использованием кода LDPC, в котором кодер LDPC выполняет кодирование с использованием кода LDPC, имеющего длину кода 4320 битов и скорость кодирования 1/2, матрица Н проверки на четность кода LDPC выполнена посредством размещения элементов 1 информационной матрицы, определенных на основе таблицы исходного значения матрицы проверки на четность для матрицы Н проверки на четность, представляющей положения элементов 1 информационной матрицы в соответствии с длиной информации, длиной кода и скоростью кодирования для каждых 72 столбцов, в направлении столбцов в период 72 столбца (патент RU2574828, МПК H03M 13/11, публ.10.02.2016г.).
Недостатком данного способа является большая вычислительная сложность алгоритма кодирования. Предлагаемый способ позволяет достичь меньшей задержки при передаче сообщений.
Наиболее близким к предлагаемому способу является способ для кодирования и декодирования канала в системе связи с использованием кодов с малой плотностью проверок на четность LDPC, в котором определяют параметры для разработки кода LDPC и формируют первую матрицу проверки четности квазициклического кода LDPC в соответствии с упомянутыми определенными параметрами, создают вторую матрицу проверки четности посредством удаления заранее заданной доли части четности в первой матрице проверки четности и создают третью матрицу проверки четности посредством переупорядочивания второй матрицы проверки четности (патент RU2450442, МПК H03M 13/11, публ.10.05.2012г.).
Недостатком данного способа является неоптимальность весовых распределений проверочной матрицы, а также большая вычислительная сложность алгоритма кодирования. Предлагаемый способ позволяет достичь меньшей задержки при передаче сообщений.
Наиболее близким к предлагаемому способу является способ, в котором для передачи сигнала считывают сохраненную матрицу проверки четности, выполняют LDPC кодирование сигнала, используя сохраненную матрицу проверки четности, при этом кодовая скорость составляет 1/2, длина кодового слова составляет 59880, и матрицу проверки четности формируют, как определено в таблице в формуле (патент RU2769945, МПК H03M 13/00, публ.11.04.2022г. – прототип).
Недостатком данного способа является недостаточная вычислительная эффективность кодирования. Предлагаемый способ позволяет достичь меньшей задержки при передаче сообщений и повышенной вычислительной эффективности кодера при программной реализации за счёт того, что она может быть преобразована к IRA виду.
Технический результат предлагаемого способа заключается в уменьшении задержки при передаче сообщений.
Технический результат достигается тем, что в способе кодирования канала в системе связи, использующей код с малой плотностью проверок четности LDPC, содержащий этапы, на которых считывают сохраненную матрицу проверки четности и выполняют LDPC кодирование сигнала, используя сохраненную матрицу проверки четности, введена отличающаяся матрица проверки четности с отличающейся длиной кодового слова и иным принципом расположения значащих квадрантов.
Сущность изобретения заключается в том, что при передаче сигнала считывают сохраненную матрицу проверки четности и выполняют LDPC кодирование сигнала, используя сохраненную матрицу проверки четности, причем матрицы проверки четности формируют, как определено в таблице 1.
При проведении патентных исследований не обнаружены решения, идентичные заявленному, следовательно, предложенное решение соответствует критерию "новизна". Сущность изобретения не следует явным образом из известных решений, следовательно, предложенное изобретение соответствует критерию "изобретательский уровень".
Предлагаемый способ применяют следующим образом. Для передачи сигнала считывают сохраненную матрицу проверки четности. Выполняют LDPC кодирование сигнала, используя сохраненную матрицу проверки четности. Формат сжатой проверочной матрицы имеет следующий вид:

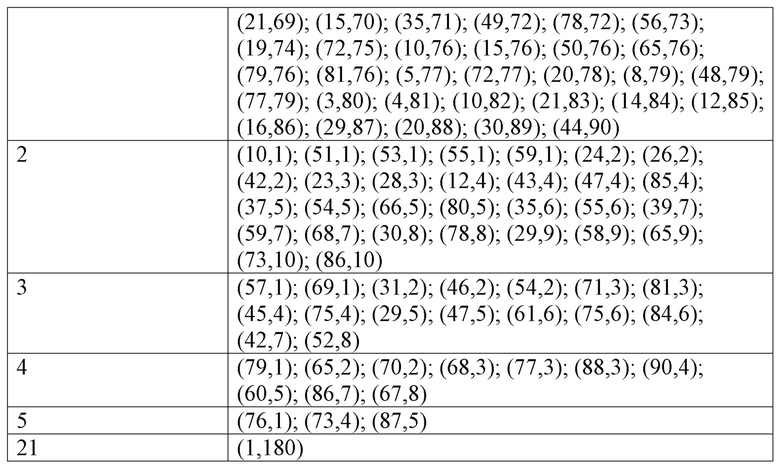
причём параметры m и n определяются тройкой чисел: скоростью кодирования (R), длиной кодового слова (N) и размером цикрулянта (q). При R = ½, N = 3960 и q = 22, m = (1-R)N/q; m = 90; n = N/q; n = 180. Сформировать матрицу Hb возможно по таблице 1. Для её расширения до проверочной матрицы H достаточно каждый циркулянт заменить единичной диагональной матрицей размером q на q, сдвиг главной диагонали которой равен cij.
Таблица 1.
циркулянтами cij
(16,2); (27,2); (58,2); (2,3); (9,3); (12,3); (15,3); (62,3);
(74,3); (6,4); (19,4); (22,4); (25,4); (63,4); (1,5); (15,5);
(20,5); (33,5); (77,5); (7,6); (11,6); (23,6); (27,6); (38,6);
(50,6); (57,6); (72,6); (4,7); (18,7); (21,7); (36,7); (48,7);
(62,7); (72,7); (79,7); (2,8); (14,8); (22,8); (26,8); (34,8);
(46,8); (48,8); (64,8); (5,9); (13,9); (16,9); (219); (25, 9);
(34,9); (37,9); (47,9); (49,9); (81,9); (89,9); (12,10);
(19,10); (32,10); (40,10); (44,10); (51,10); (64,10);
(66,10); (69,10); (90,10); (20,11); (82,11); (58,12);
(90,12); (17,13); (43,13); (7,14); (83,14); (22,15);
(71,15); (13,16); (86,16); (33,17); (88,17); (28,18);
(87,18); (30,19); (62,19); (7,20); (60,20); (18,21);
(83,21); (10,22); (76,22); (16,23); (67,23); (46,24);
(84,24); (8,25); (64,25); (1,26); (79,26); (33,27); (48,27);
(22,28); (37,28); (31,29); (89,29); (24,30); (72,30);
(38,31); (81,31); (2,32); (41,32); (11,33); (66,33);
(15,34); (75,34); (25,35); (74,35); (23,36); (65,36);
(3,37); (85,37); (45,38); (68,38); (6,39); (71,39);
(12,40); (50,40); (4,41); (47,41); (52,42); (61,42);
(14,43); (89,43); (5,44); (82,44); (17,45); (51,45);
(11,46); (63,46); (58,47); (85,47); (30,48); (45,48);
(5,49); (77,49); (34,50); (71,50); (43,51); (74,51); (7,52);
(32,52); (16,53); (62,53); (27,54); (83,54); (9,55);
(80,55); (37,56); (86,56); (2,57); (55,57); (23,58);
(79,58); (1,59); (61,59); (18,60); (70,60); (4,61); (87,61);
(8,62); (90,62); (12,63); (60,63); (13,64); (68,64);
(14,65); (84,65); (26,66); (76,66); (25,67); (88,67);
(31,68); (73,68); (3,69); (75,69); (6,70); (57,70); (20,71);
(46,71); (40,72); (47,73); (65,73); (10,74); (28,74);
(63,75); (81,75); (3,76); (27,76); (32,76); (35,76);
(43,76); (53,76); (62,76); (70,76); (84,76); (88,76);
(1,77); (9,77); (14,77); (17,77); (25,77); (29,77); (31,77);
(40,77); (53,77); (57,77); (60,77); (75,77); (78,77);
(83,77); (4,78); (22,78); (24,78); (28,78); (30,78);
(33,78); (38,78); (41,78); (44,78); (52,78); (54,78);
(59,78); (67,78); (85,78); (89,78); (6,79); (11,79);
(13,79); (18,79); (28,79); (39,79); (42,79); (46,79);
(51,79); (61,79); (74,79); (80,79); (88,79); (1,80);
(19,80); (23,80); (26,80); (36,80); (41,80); (43,80);
(45,80); (49,80); (55,80); (71,80); (73,80); (80,80);
(82,80); (87,80); (2,81); (7,81); (37,81); (51,81); (58,81);
(63,81); (78,81); (84,81); (5,82); (15,82); (18,82);
(23,82); (31,82); (68,82); (85,82); (90,82); (9,83);
(26,83); (35,83); (54,83); (61,83); (63,83); (69,83);
(77,83); (8,84); (24,84); (45,84); (62,84); (66,84);
(76,84); (81,84); (86,84); (6,85); (27,85); (47,85);
(52,85); (55,85); (64,85); (75,85); (79,85); (2,86);
(28,86); (36,86); (53,86); (56,86); (11,87); (32,87);
(49,87); (59,87); (65,87); (13,88); (48,88); (57,88);
(70,88); (73,88); (3,89); (34,89); (40,89); (42,89);
(50,89); (37,90); (46,90); (60,90); (68,90); (72,90);
(1,91); (2,91); (2,92); (3,92); (3,93); (4,93); (4,94);
(5,94); (5,95); (6,95); (6,96); (7,96); (7,97); (8,97);
(8,98); (9,98); (9,99); (10,99); (10,100); (11,100);
(11,101); (12,101); (12,102); (13,102); (13,103);
(14,103); (14,104); (15,104); (15,105); (16,105);
(16,106); (17,106); (17,107); (18,107); (18,108);
(19,108); (19,109); (20,109); (20,110); (21,110);
(21,111); (22,111); (22,112); (23,112); (23,113);
(24,113); (24,114); (25,114); (25,115); (26,115);
(26,116); (27,116); (27,117); (28,117); (28,118);
(29,118); (29,119); (30,119); (30,120); (31,120);
(31,121); (32,121); (32,122); (33,122); (33,123);
(34,123); (34,124); (35,124); (35,125); (36,125);
(36,126); (37,126); (37,127); (38,127); (38,128);
(39,128); (39,129); (40,129); (40,130); (41,130);
(41,131); (42,131); (42,132); (43,132); (43,133);
(44,133); (44,134); (45,134); (45,135); (46,135);
(46,136); (47,136); (47,137); (48,137); (48,138);
(49,138); (49,139); (50,139); (50,140); (5,1140);
(51,141); (52,141); (52,142); (53,142); (53,143);
(54,143); (54,144); (55,144); (55,145); (56,145);
(56,146); (57,146); (57,147); (58,147); (58,148);
(59,148); (59,149); (60,149); (60,150); (61,150);
(61,151); (62,151); (62,152); (63,152); (63,153);
(64,153); (64,154); (65,154); (65,155); (66,155);
(66,156); (67,156); (67,157); (68,157); (68,158);
(69,158); (69,159); (70,159); (70,160); (71,160);
(71,161); (72,161); (72,162); (73,162); (73,163);
(74,163); (74,164); (75,164); (75,165); (76,165);
(76,166); (77,166); (77,167); (78,167); (78,168);
(79,168); (79,169); (80,169); (80,170); (81,170);
(81,171); (82,171); (82,172); (83,172); (83,173);
(84,173); (84,174); (85,174); (85,175); (86,175);
(86,176); (87,176); (87,177); (88,177); (88,178);
(89,178); (89,179); (90,179); (90,180)
(3,3); (18,3); (20,3); (49,3); (52,3); (32,4); (34,4); (36,4);
(61,4); (67,4); (8,5); (17,5); (39,5); (41,5); (50,5); (9,6);
(45,6); (64,6); (70,6); (89,6); (6,7); (31,7); (38,7); (56,7);
(66,7); (10,8); (24,8); (60,8); (69,8); (74,8); (82,8); (7,9);
(17,9); (76,9); (87,9); (16,10); (33,10); (56,10); (71,10);
(76,10); (83,10); (25,11); (74,12); (38,13); (67,14);
(42,15); (82,16); (57,17); (78,18); (58,19); (19,20);
(55,21); (39,22); (35,23); (73,24); (36,25); (34,26);
(43,27); (27,28); (77,29); (49,30); (69,31); (32,32);
(53,33); (54,34); (70,35); (39,36); (17,37); (51,38);
(29,39); (21,40); (9,41); (56,42); (19,43); (44,44);
(26,45); (41,46); (80,47); (39,48); (36,49); (59,50);
(66,51); (24,52); (22,53); (48,54); (67,55); (53,56);
(29,57); (54,58); (44,59); (40,60); (69,61); (50,62);
(38,63); (33,64); (42,65); (59,66); (64,67); (52,68);
(21,69); (15,70); (35,71); (49,72); (78,72); (56,73);
(19,74); (72,75); (10,76); (15,76); (50,76); (65,76);
(79,76); (81,76); (5,77); (72,77); (20,78); (8,79); (48,79);
(77,79); (3,80); (4,81); (10,82); (21,83); (14,84); (12,85);
(16,86); (29,87); (20,88); (30,89); (44,90)
(42,2); (23,3); (28,3); (12,4); (43,4); (47,4); (85,4);
(37,5); (54,5); (66,5); (80,5); (35,6); (55,6); (39,7);
(59,7); (68,7); (30,8); (78,8); (29,9); (58,9); (65,9);
(73,10); (86,10)
(45,4); (75,4); (29,5); (47,5); (61,6); (75,6); (84,6);
(42,7); (52,8)
(60,5); (86,7); (67,8)
Предлагаемый способ позволяет достичь меньшей задержки при передаче сообщений в 1,09 раза по сравнению с первым приведенным в качестве аналога способом, в 4,07 – 16,28 раза по сравнению со вторым приведенным в качестве аналога способом в зависимости от длины кодового слова и в 15,04 по сравнению с третьим приведенным в качестве аналога способом, указанным в качестве прототипа.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ кодирования канала в системе связи, использующей LDPC-код | 2020 |
|
RU2769945C2 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ КАНАЛА В СИСТЕМЕ СВЯЗИ С ИСПОЛЬЗОВАНИЕМ КОДОВ С НИЗКОЙ ПЛОТНОСТЬЮ ПРОВЕРОК НА ЧЕТНОСТЬ | 2009 |
|
RU2450442C2 |
| СПОСОБ И УСТРОЙСТВО ПОМЕХОУСТОЙЧИВОГО ДЕКОДИРОВАНИЯ СИГНАЛОВ, ПОЛУЧЕННЫХ С ИСПОЛЬЗОВАНИЕМ КОДА ПРОВЕРКИ НА ЧЕТНОСТЬ С НИЗКОЙ ПЛОТНОСТЬЮ | 2013 |
|
RU2522299C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КАНАЛЬНОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ В СИСТЕМЕ СВЯЗИ С ИСПОЛЬЗОВАНИЕМ КОДОВ ПРОВЕРОК НА ЧЕТНОСТЬ С МАЛОЙ ПЛОТНОСТЬЮ | 2008 |
|
RU2491728C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КАНАЛЬНОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ В СИСТЕМЕ СВЯЗИ С ИСПОЛЬЗОВАНИЕМ КОДОВ ПРОВЕРОК НА ЧЕТНОСТЬ С МАЛОЙ ПЛОТНОСТЬЮ | 2008 |
|
RU2491727C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ КАНАЛА В СИСТЕМЕ СВЯЗИ С ИСПОЛЬЗОВАНИЕМ КОДОВ ПРОВЕРОК НА ЧЕТНОСТЬ С МАЛОЙ ПЛОТНОСТЬЮ | 2008 |
|
RU2446585C2 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ КОДОВ С НИЗКОЙ ПЛОТНОСТЬЮ ПРОВЕРОК НА ЧЕТНОСТЬ | 2017 |
|
RU2739465C2 |
| СПОСОБ ПОМЕХОУСТОЙЧИВОГО ДЕКОДИРОВАНИЯ СИГНАЛОВ, ПОЛУЧЕННЫХ С ИСПОЛЬЗОВАНИЕМ ПАРАЛЛЕЛЬНОГО КАСКАДНОГО КОДА ПРОВЕРКИ НА ЧЕТНОСТЬ С НИЗКОЙ ПЛОТНОСТЬЮ | 2011 |
|
RU2461964C1 |
| УСТРОЙСТВО И СПОСОБ ДЛЯ ГЕНЕРИРОВАНИЯ МАТРИЦЫ ПРОВЕРКИ ЧЕТНОСТИ В СИСТЕМЕ СВЯЗИ С ИСПОЛЬЗОВАНИЕМ ЛИНЕЙНЫХ БЛОЧНЫХ КОДОВ И УСТРОЙСТВО ПЕРЕДАЧИ/ПРИЕМА И СПОСОБ ДЛЯ ИСПОЛЬЗОВАНИЯ ЭТОГО | 2010 |
|
RU2537806C2 |
| СПОСОБ И УСТРОЙСТВО СОХРАНЕНИЯ ДАННЫХ | 2012 |
|
RU2608958C2 |
Изобретение относится к телекоммуникационным и эфирным видеоинформационным системам вещания. Технический результат заключается в уменьшении задержки при передаче сообщений. Технический результат достигается за счет того, что при передаче сигнала считывают сохраненную матрицу проверки четности и выполняют LDPC кодирование сигнала, используя сохраненную матрицу проверки четности, причем матрицу проверки четности формируют при помощи сжатой матрицы, приведенной в приложенной таблице. 4 ил.
Способ кодирования канала в системе связи, использующей LDPC-код, содержащий этапы, на которых:
считывают сохраненную матрицу проверки четности; и
выполняют LDPC кодирование сигнала, используя сохраненную матрицу проверки четности,
отличающийся тем, что кодовая скорость составляет 1/2, длина кодового слова составляет 3980, индексация с 1, размер циркулянта равен 22 и матрицу проверки четности формируют при помощи сжатой матрицы вида

определенной в нижеследующей таблице, причём параметры m и n определяются тройкой чисел: скоростью кодирования (R), длиной кодового слова (N) и размером цикрулянта (q) (при R = 1/2, N = 3960 и q = 22, m = (1-R)N/q; m = 90; n = N/q; n = 180), заменяя при этом каждый циркулянт единичной диагональной матрицей размером q на q, сдвиг главной диагонали которой равен cij



| СПОСОБЫ И СИСТЕМЫ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ LDPC КОДОВ | 2016 |
|
RU2716044C1 |
| WO 2006062351 A1, 15.06.2006 | |||
| US 20120290892 A1, 15.11.2012 | |||
| US 20090199068 A1, 06.08.2009 | |||
| US 20150067440 A1, 05.03.2015 | |||
| КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ LDPC ПАКЕТОВ ПЕРЕМЕННЫХ РАЗМЕРОВ | 2008 |
|
RU2443053C2 |
| УСТРОЙСТВО И СПОСОБ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ БЛОЧНОГО КОДА РАЗРЕЖЕННОГО КОНТРОЛЯ ЧЕТНОСТИ | 2005 |
|
RU2348103C2 |
Авторы
Даты
2023-03-13—Публикация
2022-12-14—Подача