Изобретение относится к области шифрования информации, а именно к блочному способу шифрования, при котором ключевая матрица квадратного размера фактически не вычисляется. Способ может использоваться в режиме одноразового ключа. Предлагается модификация шифра с инволютивной ключевой матрицей размера открытого текста T, представленной как произведение Кронекера K элементарных инволютивных матриц, что позволяет избежать обращения ключевой матрицы для дешифрования.
Известны различные способы блочного шифрования, описанные в следующих патентах:
RU 2728527 C1 «Способ и устройство кодирования», в котором представляется способ и устройство кодирования информации в системе связи при передаче данных.
RU 2738321 C1 «Способ криптографического преобразования и устройство для его осуществления», в котором раскрыт способ криптографического преобразования для обработки большого массива, пакетов или потоков данных на основе программно-аппаратной реализации в микропроцессоре алгоритма блочного шифрования AES, включающий преобразование исходных данных в структуру S, состоящую из 16-байтных блоков.
RU 2748964 C2 «Способ безопасной передачи запрашиваемых данных и реализующая его система», в котором описан способ безопасной передачи запрашиваемых данных от устройства доверенной стороны к устройству третьей стороны.
А также статьи:
«Духнич, Е.И., Чефранов А.Г. Использование кронекерова произведения матриц для модификации криптографических алгоритмов / Е.И. Духнич, А.Г. Чефранов // ГМУ им. адм. Ф.Ф. Ушакова. Эксплуатация морского транспорта - 2020. - № ГМУ им. адм. Ф.Ф. Ушакова. Эксплуатация морского транспорта - 2020. - № 2(95)2020- С. 45-52. - DOI: 10.34046/aumsuomt95/23»
«Духнич, Е.И. Аппаратурно-ориентированный алгоритм для быстрого умножения кронекерова произведения матриц на вектор / Е.И. Духнич, А.Г. Чефранов // Известия ЮФУ. Технические науки. - 2020. - № 7(217). - С. 134-138. - DOI 10.18522/2311-3103-2020-7-45-52.»
Наиболее близким по техническому решению является метод, принятый за прототип:
RU 2715411 C2 «Цифровой комплекс спутниковой системы связи», в котором применяются блочные шифры разового пользования, т.е. шифры, ключевой оператор которых явно зависит от временного параметра t. Характер изменений этого параметра определяет временные интервалы «разового пользования» ключевым материалом, на примере шифра Л. Хилла.
Одноразовый блокнот - криптосистема, использующая ключи «разового пользования», является абсолютно стойким шифром, если соблюдаются следующие свойства:
Первое свойство: ключ генерируется для каждого сообщения, каждый ключ используется только один раз;
Второе свойство: размер ключевой матрицы равен или больше длины сообщения T;
Третье свойство: ключ статистически надёжен, то есть вероятности появления каждого из возможных символов равны, символы в ключевой последовательности независимы и случайны.
Метод, описанный в прототипе, имеет следующие недостатки:
Первый недостаток: необходимость обращения ключевой матрицы при дешифровании;
Второй недостаток: квадратичные сложность вычислений и объем памяти для хранения ключевой матрицы (по отношению к размеру сообщения), т.к. умножение квадратной матрицы размера 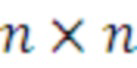 на вектор имеет вычислительную сложность O(n2).
на вектор имеет вычислительную сложность O(n2).
Для устранения первого недостатка в патенте № RU 2728527 C1 «Способ и устройство кодирования» было предложено использование инволютивных (обратных самим себе) матриц в блочных шифрах в качестве ключевых, с целью устранения необходимости вычисления матрицы, обратной ключевой, для дешифрования.
Однако, к сожалению, как аналоги, так и прототип не обеспечивают достаточную эффективность шифрования, так как для шифрования и расшифровки сообщения необходимо проводить избыточные арифметические операции.
Технической задачей настоящего изобретения является повышение эффективности и криптографической стойкости алгоритма шифрования, устранение недостатков аналогов и прототипа путем модификации метода, предложенного Л. Хиллом.
Техническая задача достигается тем, что в заявленном способе блочного шифрования и дешифрования данных с помощью шифра Л. Хилла, задают вектор входного сообщения, генерируют ключевую матрицу в виде инволютивной матрицы, отличающийся тем, что генерацию ключевой матрицы А размером Т с использованием Кронекерова произведения K элементарных инволютивных 2×2 матриц 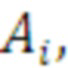 где K=
где K=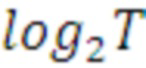 , при этом генерируемая матрица ключа имеет выражение:
, при этом генерируемая матрица ключа имеет выражение:
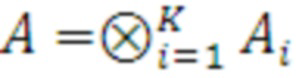 ,
,
шифрование производят путем использования специального алгоритма совмещения вычисления инволютивной матрицы ключа А и перемножения ее на вектор входного сообщения, а шифру придают свойства абсолютно стойкого шифра, действующего в «одноразовом» режиме, для чего ключ генерируют для каждого сообщения и каждый ключ используют только один раз, при этом размер ключевой матрицы равен или больше размера сообщения, а статистическую надежность ключа обеспечивают тем, что символы в ключевой последовательности независимы и случайны, вероятности появления каждого из возможных символов равны, причем, «одноразовый» режим обеспечивают достаточно большим переменным размером блока, выполненным так, что один блок покрывает весь открытый текст, что исключает атаки, основанные на использовании уже известных пар «открытый текст-зашифрованный текст», полученных с помощью одного и того же ключа, при этом размер блока задают размером ключевой матрицы А, дешифрование производят путем использования специального алгоритма совмещения вычисления инволютивной матрицы ключа А и перемножения ее с вектором зашифрованного входного сообщения, причем Кронекерово произведения инволютивных матриц является также инволютивной матрицей, что исключает при дешифровании этап вычисления обратной матрицы.
Технический результат заключается в том, что в предложенном алгоритме происходит повышение криптостойкости за счет придания шифру свойств абсолютно стойкого шифра на примере метода «Одноразовый блокнот».
Технический результат достигается тем, что вместо фактического вычисления ключевой матрицы инволютивные элементарные матрицы итеративно умножаются на открытый текст длины T за время 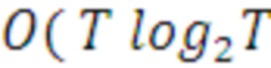 ) при сложности памяти
) при сложности памяти 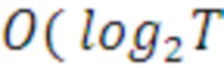 ).
).
В заявляемом способе первое свойство «Одноразового блокнота» обеспечивается достаточно большим переменным размером блока, таким, что один блок покрывает весь открытый текст, что исключает атаки, основанные на использовании уже известных пар «открытый текст-зашифрованный текст», полученных с помощью одного и того же ключа.
Второе свойство «Одноразового блокнота» обеспечивается тем, что размер блока задается размером ключевой матрицы, формируемой в виде Кронекерова произведения (КП) элементарных (2×2) матриц.
Выполнение двух вышеуказанных свойств обеспечивает статистическую надежность ключа (третье свойство «Одноразового блокнота»).
В заявляемом техническом решении предложено формирование ключевой матрицы как КП инволютивных элементарных матриц (2×2) в форме:
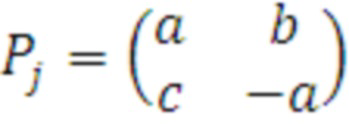 , (1)
, (1)
где j=1,2,…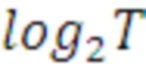 , a и b - произвольные числа из ZN (берутся из ключа свои для каждого j ), причем b -нечетное, если N=2d, а
, a и b - произвольные числа из ZN (берутся из ключа свои для каждого j ), причем b -нечетное, если N=2d, а
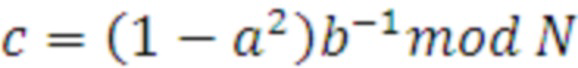 .
.
Известно свойство КП, что результатом КП инволютивных матриц является также инволютивная матрица.
Для устранения второго недостатка предлагается построение алгоритма, ускоряющего процессы формирования КП и умножения вектора на него. Алгоритм позволяет совместить во времени эти процедуры. Таким образом, матрица КП в явном виде фактически не рассчитывается. Вместо этого матрицы-сомножители КП итеративно умножаются на компоненты вектора за время O(nlog2n), где n= T.
Таким образом, формирование ключевой матрицы как КП элементарных инволютивных матриц существенно повышает эффективность шифра за счет исключения предварительного отдельного вычисления КП и его обращения, а также отсутствия необходимости хранения в памяти ключевой матрицы (КП). При этом вычислительная сложность и расходы памяти будут соответственно равны O(nlogn) и O(n) в отличие от квадратичной сложности других модификаций шифра Хилла, где n- длина сообщения.
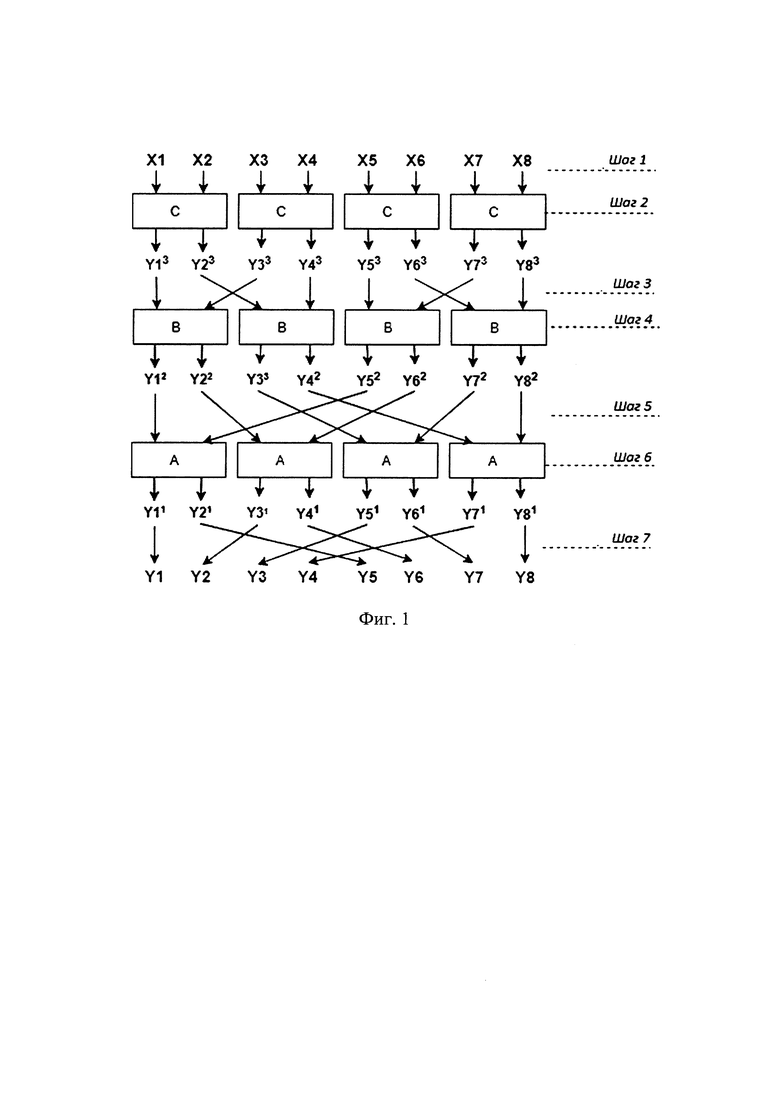
Сущность изобретения поясняется графическим материалом, где на фиг. 1 представлена схема вычислений для сообщения n=8, КП порядка 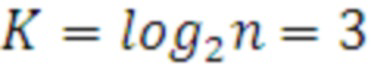 , причем:
, причем:
X1-8 - байты вектора входного сообщения;
C, B, A - матрицы P1, P2, P3, полученные по формуле (1);
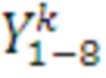 - результат произведения частей векторов на матрицы С (k=3), В (k=2), А (k=1);
- результат произведения частей векторов на матрицы С (k=3), В (k=2), А (k=1);
Y1-8 - байты зашифрованного сообщения.
Шифрование выполняется как вычисление произведения КП на вектор Х, которое математически описывается в виде:
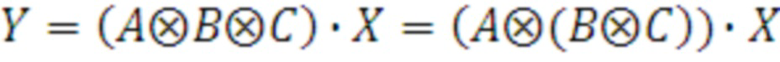 (2)
(2)
Однако вместо вычисления КП и выражения (2) происходит выполнение следующей последовательности шагов:
1. Вектор Х делится на n/2 частей - 2-мерных векторов 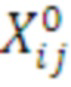 , где i=1,3,5,7, j=2,4,6,8.
, где i=1,3,5,7, j=2,4,6,8.
2. Выполняется умножение этих векторов на матрицу C=P1 (1):
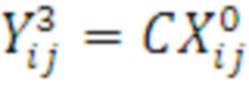
3. Выполняется переиндексация элементов результирующих векторов умножением их на перестановочную матрицу 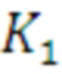 так, чтобы i=1,2,5,6, j=3,4,7,8:
так, чтобы i=1,2,5,6, j=3,4,7,8:
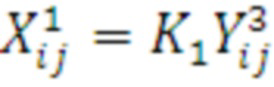
4. Выполняется умножение этих векторов на матрицу B=P2:
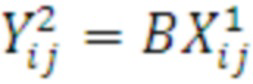
5. Выполняется переиндексация элементов результирующих векторов умножением их на перестановочную матрицу 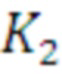 так, чтобы i=1,3,2,4, j=5,7,6,8:
так, чтобы i=1,3,2,4, j=5,7,6,8:
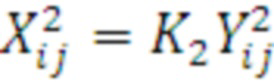
6. Выполняется умножение этих векторов на матрицу A=P3:
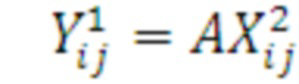
7. Выполняется переиндексация элементов результирующих векторов умножением их на перестановочную матрицу 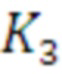 так, чтобы i=1,5,2,6, j=3,7,4,8:
так, чтобы i=1,5,2,6, j=3,7,4,8:
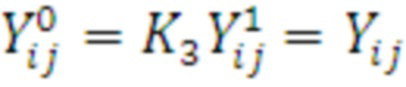
8. Из полученных двумерных векторов 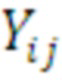 конкатенацией формируется результирующий вектор Y выражения (2).
конкатенацией формируется результирующий вектор Y выражения (2).
Таким образом, на фиг. 1 преобразования (2) по шагам 1-8 (сверху вниз) представлены в виде схемы с топологией гиперкуба, где все матрицы А, В, С обозначены прямоугольниками и для каждого из четырех экземпляров каждой из этих матриц указаны соответствующие входные и выходные данные, причем умножения на перестановочные матрицы показаны соединительными линиями между уровнями (рядами прямоугольников). Следует отметить, что дешифрование описывается точно такой же схемой вычислений.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОТОЧНОГО ШИФРОВАНИЯ ДАННЫХ | 2005 |
|
RU2291578C1 |
| Повышение неоднозначности | 2016 |
|
RU2737917C1 |
| СПОСОБ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ В ВИДЕ УЛЬТРАСЖАТОГО НАНОБАР-КОДА (ВАРИАНТЫ) | 2013 |
|
RU2656734C2 |
| ЭФФЕКТИВНОЕ ШИФРОВАНИЕ И АУТЕНТИФИКАЦИЯ ДЛЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ | 2003 |
|
RU2340108C2 |
| СПОСОБ ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ | 1997 |
|
RU2119260C1 |
| СПОСОБ ПОТОЧНОГО ШИФРОВАНИЯ ДАННЫХ | 2001 |
|
RU2239290C2 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ БЛОКОВ ЦИФРОВЫХ ДАННЫХ | 1997 |
|
RU2140709C1 |
| СПОСОБ ПОТОЧНОГО ШИФРОВАНИЯ ДАННЫХ | 2009 |
|
RU2423799C2 |
| ЭФФЕКТИВНОЕ ШИФРОВАНИЕ И АУТЕНТИФИКАЦИЯ ДЛЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ | 2003 |
|
RU2336646C2 |
| СПОСОБ ИТЕРАТИВНОГО БЛОЧНОГО ШИФРОВАНИЯ ДВОИЧНЫХ ДАННЫХ | 2001 |
|
RU2206961C2 |
Изобретение относится к области шифрования информации. Технический результат заключается в повышении криптографической стойкости алгоритма шифрования. Такой результат достигается модификацией шифра с инволютивной ключевой матрицей размера открытого текста, представленной как произведение Кронекера K элементарных инволютивных матриц, позволяющего избежать обращения ключевой матрицы для дешифрования. 1 ил.
Способ блочного шифрования с использованием Кронекерова произведения инволютивных матриц, основанный на шифровании и дешифровании данных с помощью шифра Л. Хилла, в котором задают вектор входного сообщения, генерируют матрицу ключа в виде инволютивной матрицы, отличающийся тем, что производят генерацию инволютивной ключевой матрицы А размером Т с использованием умножения Кронекерова произведения K элементарных инволютивных 2×2 матриц 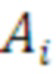 , где K=log2T, при этом генерируемая матрица ключа имеет выражение:
, где K=log2T, при этом генерируемая матрица ключа имеет выражение:
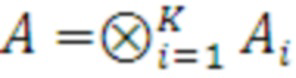 ,
,
шифрование производят путем использования алгоритма совмещения вычисления инволютивной матрицы ключа А и перемножения ее на вектор входного сообщения, а шифру придают свойства абсолютно стойкого шифра, действующего в «одноразовом» режиме, для чего ключ генерируют для каждого сообщения и каждый ключ используют только один раз, при этом длина ключа определяется значением K, а статистическую надежность ключа обеспечивают тем, что символы в ключевой последовательности независимы и случайны, вероятности появления каждого из возможных символов равны, причем, «одноразовый» режим обеспечивают достаточно большим переменным размером блока, выполненным так, что один блок покрывает весь открытый текст, что исключает атаки, основанные на использовании уже известных пар «открытый текст-зашифрованный текст», полученных с помощью одного и того же ключа, при этом размер блока задают размером ключевой матрицы А, дешифрование производят путем использования алгоритма совмещения вычисления инволютивной матрицы ключа А и перемножения ее с вектором зашифрованного входного сообщения, причем Кронекерово произведения инволютивных матриц является также инволютивной матрицей, что исключает при дешифровании этап вычисления обратной матрицы.
| ЦИФРОВОЙ КОМПЛЕКС СПУТНИКОВОЙ СИСТЕМЫ СВЯЗИ | 2018 |
|
RU2715411C2 |
| СПОСОБ ФОРМИРОВАНИЯ ЦЕЛОЧИСЛЕННЫХ ОРТОГОНАЛЬНЫХ ДЕКОРРЕЛИРУЮЩИХ МАТРИЦ ЗАДАННЫХ РАЗМЕРОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2012 |
|
RU2509364C2 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2018 |
|
RU2738321C1 |
| СПОСОБ И УСТРОЙСТВО КОДИРОВАНИЯ | 2018 |
|
RU2728527C1 |
| Многоступенчатая активно-реактивная турбина | 1924 |
|
SU2013A1 |
Авторы
Даты
2023-04-03—Публикация
2022-03-31—Подача