Изобретение относится к способам разрушающего контроля материалов, а именно к разрушающим способам реконструкции распределения по толщине продольной компоненты остаточных напряжений в упругом брусе произвольного поперечного сечения, основанных на его нарезании на тонкие полоски и измерении их деформаций. Данный способ может быть применен в машиностроении для контроля изготовления деталей с применением аддитивных технологий производства.
Объектом исследования является упругий брус прямоугольного поперечного сечения, закрепленный на жестком основании (фиг. 1, 2), по высоте которого распределена продольная компонента остаточных напряжений. Подобными объектами являются ребра оребренных панелей, широко используемых в авиационной технике; технологические остаточные напряжения в таких ребрах вызывают искажение геометрии панели и требуют подходящих способов контроля.
Известен способ определения остаточных напряжений в ребре на основании, изготовленном с помощью аддитивного производства (патент US9696142 (В2), опубл. 04.07.2017), при котором осуществляют локальные проплавления грани ребра и измеряют деформации поверхности вблизи областей расплава. Недостатки способа обусловлены горячей технологией эксперимента и ограниченностью малыми глубинами определяемых остаточных напряжений вблизи поверхности.
Известен способ определения остаточных напряжений по изменению прогиба бруса, у которого удаляются поверхностные слои (Биргер И.А. Остаточные напряжения. М.: Машгиз, 1963. 233 с.), который больше подходит для исследования упругих тел с поверхностным источником остаточных напряжений. Недостатки способа обусловлены его низкой точностью для брусьев со сплошным распределением источников остаточных напряжений (собственных деформаций).
Ближайшим по технической сущности к заявляемому изобретению является способ определения остаточных напряжений [Pekoz Т., Bjorhovde R., Errera S.J., Johnston B.G., Sherman D.R., Tall L. Determination of residual stresses: Technical memorandum of ASCE No. 6 // Guide To Stability Design Criteria For Metal Structures / Ed. R.D. Ziemian. 6th ed. 2010. P. 993-1002; ГОСТ 111603-73 Древесина. Метод определения остаточных напряжений. М.: Изд-во стандартов. 1973. 9 с.], принятый за прототип, согласно которому брус нарезают на полосы и измеряют их продольные деформации, и на основании полученных измерений длин отрезков вычисляют остаточные напряжения в материале. Продольные деформации полос, на основании которых рассчитывают остаточные напряжения, имеют малые значения, в связи с чем, для получения точных данных требуется использование высокоточного измерительного оборудования.
РАСКРЫТИЕ ИЗОБРЕТЕНИЯ
Техническая задача, на решение которой направлено заявляемое изобретение создание способа определения распределения по глубине продольной компоненты технологических остаточных напряжений и собственных деформаций в упругом брусе прямоугольного поперечного сечения, закрепленном на жестком основании.
Технический результат заявляемого изобретения заключается в увеличении точности определения распределения остаточных напряжений и собственных деформаций в упругом брусе прямоугольного поперечного сечения, закрепленном на жестком основании.
Технический результат достигается посредством осуществления способа при котором с верхней грани упругого ребра на жестком основании последовательно срезают тонкие параллельные полосы, для каждой из которых измеряют прогиб при ее продольном изгибе, и по этим данным вычисляют распределение по глубине ребра собственных деформаций и остаточных напряжений с использованием формул, приведенных далее.
Заявляемый способ определения остаточных напряжений является более точным, в отличие от аналогов, поскольку значения прогибов полос, срезаемых с ребер типичных оребренных панелей, существенно превышают изменения их длин, что позволяет осуществлять измерения без использования высокоточного оборудования.
Под собственными деформациями в упругом теле понимаются начальные неоднородные деформации неупругой природы, имеющие несовместную часть и потому вызывающие остаточные напряжения.
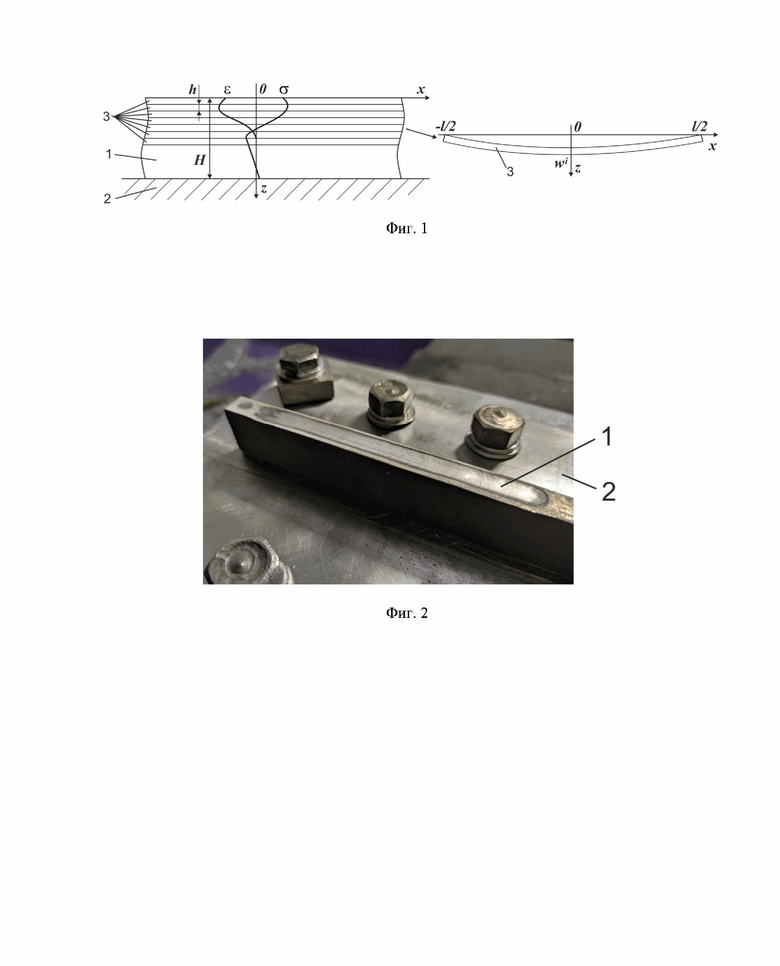
Заявляемый способ опирается на геометрическую модель ребра, в качестве которой рассматривается длинный призматический брус прямоугольного поперечного сечения с отношением сторон b/H=0,1÷1, где b - его ширина, а H - высота, закрепленный узкой гранью на жестком основании (фиг. 1, 2). Подобная схема может быть принята для ребра металлической оребренной конструкции, выращенной аддитивным производством.
Технологические собственные деформации и вызываемые ими остаточные напряжения в таком изделии возникают вследствие усадки наплавляемых слоев или послойной обработки давлением наращиваемой грани.
Для реконструкции неоднородного распределения собственных деформаций по высоте бруса предлагается способ, основанный на последовательной срезке со стороны верхней грани тонких параллельных ей слоев материала (полос) с последующим измерением их прогиба.
Для упрощения принимается Н=Nh, то есть по высоте бруса укладывается целое число N величин суммарной толщины полосы и реза h.
Вводятся обозначения х, z - декартовы координаты, направленные вдоль образующей бруса и по его толщине соответственно (фиг. 1), wi - прогиб полосы относительно концов  у=z=0.
у=z=0.
Процесс срезания полос прекращают, если прогибы отрезанных полос стабилизируются  , i=n,n+1,… или при отсутствии необходимости определения распределения собственных деформаций в оставшейся части бруса. В последнем случае измеряют прогиб оставшейся части бруса, отделенной от основания. Если прогибы отрезанных полос стабилизируются, в качестве градиента деформаций в оставшейся части
, i=n,n+1,… или при отсутствии необходимости определения распределения собственных деформаций в оставшейся части бруса. В последнем случае измеряют прогиб оставшейся части бруса, отделенной от основания. Если прогибы отрезанных полос стабилизируются, в качестве градиента деформаций в оставшейся части
бруса, отделенной от основания, следует взять прогиб последней срезанной полосы wn+1. За продольный изгиб полосы или бруса отвечает среднее значение градиента по z продольной собственной деформации полосы, обозначаемое 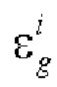 .
.
Градиенты деформации в полосах (r=1,…,n) и оставшейся части бруса (i=n+1), отделенной от основания, определяются по известным прогибам полос wi, i=1,…,n+1 приближенным соотношением
в полосах (r=1,…,n) и оставшейся части бруса (i=n+1), отделенной от основания, определяются по известным прогибам полос wi, i=1,…,n+1 приближенным соотношением

где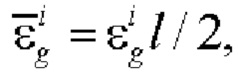
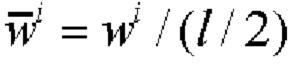 - безразмерные величины.
- безразмерные величины.
Определяют распределение по толщине бруса z∈[0,H] собственных деформаций ε(z) в виде кусочно-линейной функции со значениями εi в узлах z=0,h,…,nh, (N-n)h с помощью конечно-разностных формул
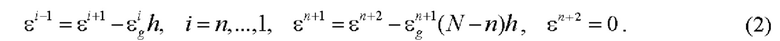
Нулевое граничное значение собственной деформации в (2) обеспечивается недеформируемостью основания, на котором закреплен брус.
Для реконструкции непрерывного распределения остаточных напряжений σ(z) по толщине бруса z ∈ [0,Н] используют формулы

- для бруса, закрепленного на жестком основании, и

- для бруса, отделенного от основания, где
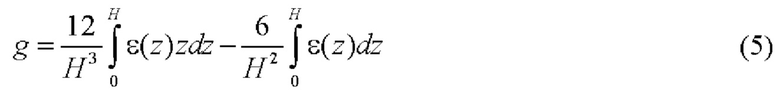
- градиент продольной деформации, а

- продольная деформация бруса.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Изобретение поясняется иллюстрирующими материалами, на которых основные элементы
обозначены следующими позициями:
1- упругий брус прямоугольного поперечного сечения,
2 - жесткое основание,
3 - пластина.
На фиг. 1 приведена схема предлагаемого способа.
Фиг. 2 прокованный брус, закрепленный на основании.
Фиг. 3 процесс нарезки слоев на электроэрозионном станке.
Фиг. 4 - прогибы полос, срезанных с бруса.
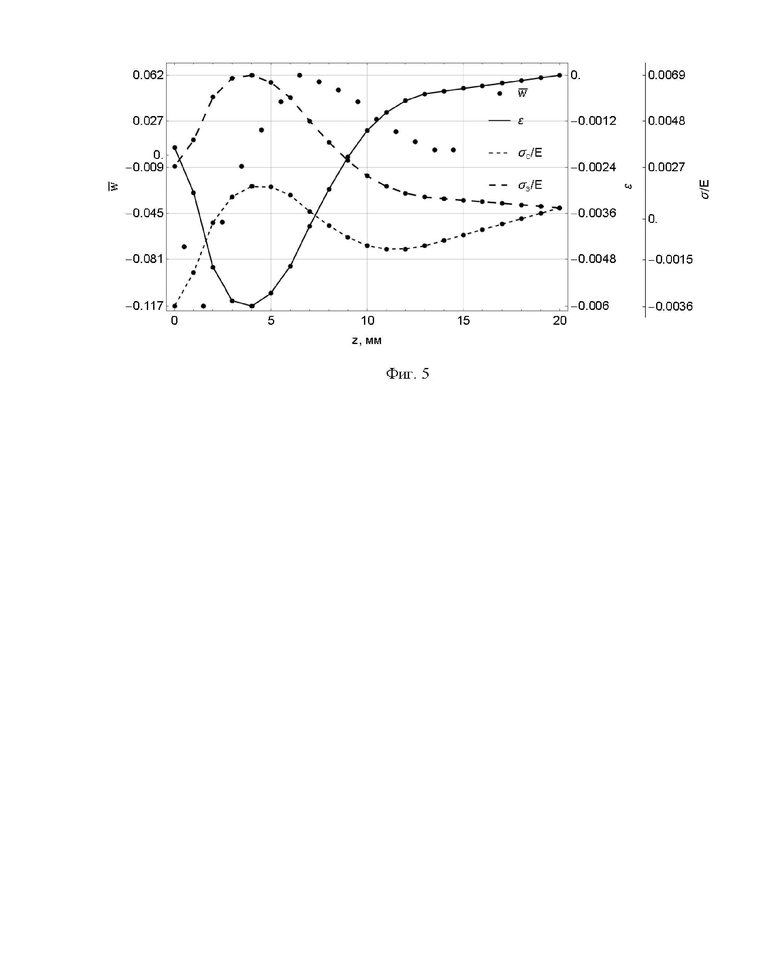
Фиг. 5 - графики реконструированных распределений собственных деформаций и остаточных напряжений для случая 1 распределения прогибов полос.
Пример осуществления изобретения.
Брус 1 размерами 25x10x250 мм, вырезанный из АМг5, был закреплен на стальной плите 2 и прокован пневматическим инструментом (фиг. 2). Со стороны прокованной грани были срезаны электроэрозионным станком семь полос 3 толщиной 1 мм (фиг. 3, 4). Прогибы полос были измерены электронным штангенциркулем. Оставшаяся часть бруса была отделена от основания и ее прогиб также измерен. По ряду дискретных значений прогибов полос 3 с использованием формул (1) - (6) были реконструированы распределения собственных деформаций и остаточных напряжений в брусе 1, закрепленном на жестком основании 2, а также в исходном брусе 1, отделенном от жесткого основания 2 (фиг. 5). В расчетах задавались значения 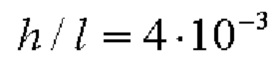 , Н=20 мм и h=1 мм.
, Н=20 мм и h=1 мм.
Следует заметить, что прогибы полос находились в диапазоне от -7 до 15 мм, а изменения длины полос после вырезки - в диапазоне 0-0,5 мм, поэтому предлагаемый способ позволяет использовать более широкую шкалу измерений по сравнению с прототипом и обеспечивает увеличение точности при сопоставимой точности измерений прогибов и длин полос.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения распределения остаточных напряжений по толщине металлоизделия с высокими поверхностными градиентами | 2024 |
|
RU2834607C1 |
| Способ определения симметричного распределения остаточных напряжений по толщине пластины | 2023 |
|
RU2818878C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ | 2011 |
|
RU2455622C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ ЗАКАЛОЧНЫХ НАПРЯЖЕНИЙ | 2012 |
|
RU2494359C1 |
| СПОСОБ ПРИБЛИЖЕННОГО ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ ТОЛЩИН | 2006 |
|
RU2380272C2 |
| СПОСОБ СТРУКТУРНОГО АНАЛИЗА ПАНЕЛЕЙ, СОСТОЯЩИХ ИЗ ИЗОТРОПНОГО МАТЕРИАЛА И УСИЛЕННЫХ ТРЕУГОЛЬНЫМИ КАРМАНАМИ | 2010 |
|
RU2563709C2 |
| СПОСОБ И УСТРОЙСТВО МОДЕЛИРОВАНИЯ УДАРНЫХ ХАРАКТЕРИСТИК ПРИ ОТРАБОТКЕ УДАРОВ НА ТРЕНАЖЕРАХ В ЕДИНОБОРСТВАХ | 2013 |
|
RU2528969C2 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО ОПРЕДЕЛЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ | 2011 |
|
RU2460057C1 |
| РАМА ПЛУГА | 1997 |
|
RU2120709C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАВЛЕНИЯ НА ГРУНТ ОСНОВАНИЯ ФУНДАМЕНТА ЗДАНИЯ ИЛИ СООРУЖЕНИЯ, НАХОДЯЩЕГОСЯ В ЭКСПЛУАТАЦИИ | 2013 |
|
RU2533742C1 |

Изобретение относится к способам разрушающего контроля материалов, а именно к разрушающим способам реконструкции распределения по толщине продольной компоненты остаточных напряжений в упругом брусе произвольного поперечного сечения, основанных на его нарезании на тонкие полоски и измерении их деформаций. Сущность: с верхней грани упругого ребра на жестком основании последовательно срезают тонкие параллельные полосы, для каждой из которых измеряют прогиб при ее продольном изгибе, и по этим данным вычисляют распределение по глубине ребра собственных деформаций и остаточных напряжений с использованием формул. Технический результат: увеличение точности определения распределения остаточных напряжений и собственных деформаций в упругом брусе прямоугольного поперечного сечения, закрепленном на жестком основании. 5 ил.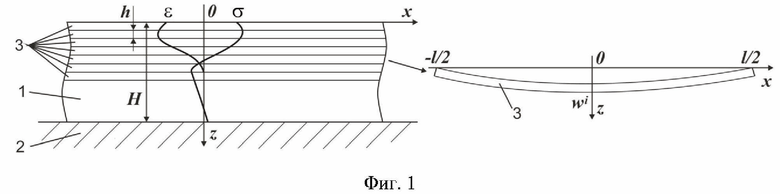
Способ определения остаточных напряжений в ребре на жестком основании, при котором с верхней грани упругого ребра последовательно срезают тонкие параллельные полосы, отличающийся тем, что
измеряют прогибы 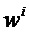
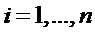
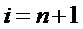
процесс срезания полос прекращают, если прогибы отрезанных полос стабилизируются 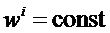
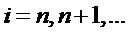
определяют градиенты деформаций 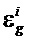
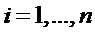
(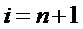
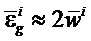
определяют распределение по толщине бруса 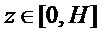
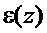
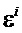

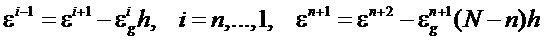
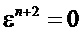
определяют распределение по толщине бруса 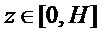
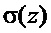
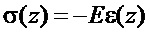
для бруса, закрепленного на жестком основании, и
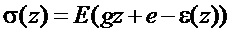
для бруса, отделенного от основания, где

- градиент продольной деформации, а

- продольная деформация бруса, где E - модуль Юнга, Н - высота бруса, h - толщина полосы и реза.
| Способ определения закалочных остаточных напряжений | 1989 |
|
SU1643928A1 |
| Способ определения внутренних напряжений в образце | 1987 |
|
SU1453159A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ ПО ХАРАКТЕРИСТИКАМ ТВЕРДОСТИ МАТЕРИАЛА | 2010 |
|
RU2435155C2 |
| WO 1998000698 A1, 08.01.1998. | |||
Авторы
Даты
2023-06-08—Публикация
2022-12-20—Подача