Изобретение относится к разрушающим способам реконструкции профиля остаточных напряжений по толщине пластины, основанным на послойном удалении материала с поверхности вырезанной из нее полоски и измерении ее прогиба.
Объектом исследования является упругая пластина с симметричным распределением по толщине остаточных напряжений, наведенных двухсторонней поверхностной обработкой. Примерами подобных объектов являются лопатки авиационных двигателей, подвергнутые поверхностной пластической деформацией (дробеструйной, ультразвуковой, лазерной, обкатыванием, выглаживанием) или термической обработке для повышения усталостного ресурса.
Известен способ реконструкции профиля остаточных напряжений вблизи поверхности детали [Dawidenkow N. Berechnung der Restspannungen in kaltgezogenen Rohren // Zeitschrift fur Metallkunde. 1932. Vol. 24, No.2. Р. 25-29. Биргер И.А. Остаточные напряжения. М.: Машгиз, 1963. 233 с.], который заключается в вырезании полоски, постепенном удалении материала с исследуемой ее поверхности с измерением прогиба и использовании реконструктивных выражений Давиденкова - Биргера. Данный способ не позволяет непосредственно определять распределение остаточных напряжений по толщине пластины с двухсторонним поверхностным слоем остаточных напряжений (без ее продольного разрезания, которое не всегда возможно). В отличие от аналога, предлагаемый способ позволяет реконструировать профиль остаточных напряжений в пластине с двухсторонним поверхностным слоем остаточных напряжений без ее продольного разрезания, что достигается за счет использования соответствующих реконструктивных выражений.
РАСКРЫТИЕ ИЗОБРЕТЕНИЯ
Техническая задача, на решение которой направлено изобретение - реконструкция распределения по толщине пластины остаточных напряжений, вызванных двухсторонней обработкой.
Технический результат - возможность реконструкции симметричного профиля остаточных напряжений в пластине с использованием данных прогиба полоски при одностороннем стравливании материала без ее продольного разрезания.
Технический результат достигается способом, который включает следующие операции:
1) постепенное удаление материала с одной из плоскостей полоски с использованием любой установки, в которой реализован метод Давиденкова - Биргера (АПООН, Меркулон, Пион и т.д.) с сопутствующим измерением ее прогиба и
2) вычисления по этим данным профилей собственных деформаций и остаточных напряжений с использованием оригинальных реконструктивных формул, приведенных ниже.
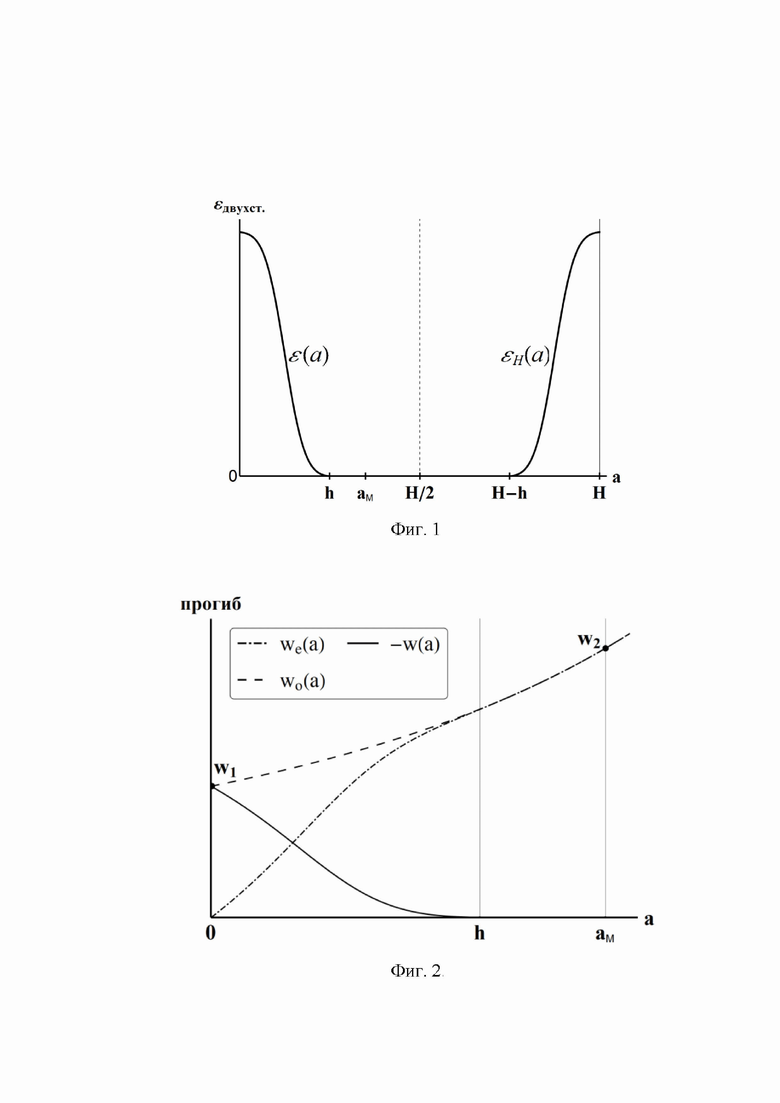
Пусть полоса длиной L и толщиной Н имеет нулевой прогиб и содержит профиль тангенциальных собственных (неупругих) несовместных деформаций, состоящий из двух симметричных отрезков: ε(a), 0≤a≤h и εH(a) = ε(Н - a), Н-h≤a≤Н (фиг. 1), где h есть толщина слоя, a - координата, изменяющаяся по толщине полосы.
С плоскости полосы a=0 постепенно удаляется материал и параллельно замеряется зависимость ее продольного прогиба we(a) от толщины удаленного слоя, который полоса приобретает. Для корректной работы метода, максимальная толщина удаленного слоя aм должна быть больше глубины слоя собственных деформаций h, признак того, что удален весь слой собственных деформаций и способ избежать этого ограничения указаны ниже.
Задача определения профиля собственных деформаций ε(а), 0≤а≤h сводится к более простому случаю односторонней обработки. Зависимость прогиба полосы от толщины удаленного слоя в случае односторонней обработки w(а) связана с we(а) как
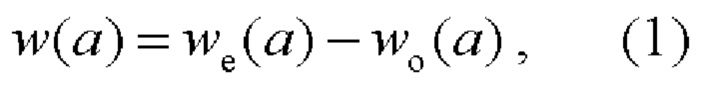
где

- прогиб полосы с односторонним профилем собственных деформаций εH(а)=ε(Н - а), Н -h≤а≤Н, константы в (2) находятся по формулам

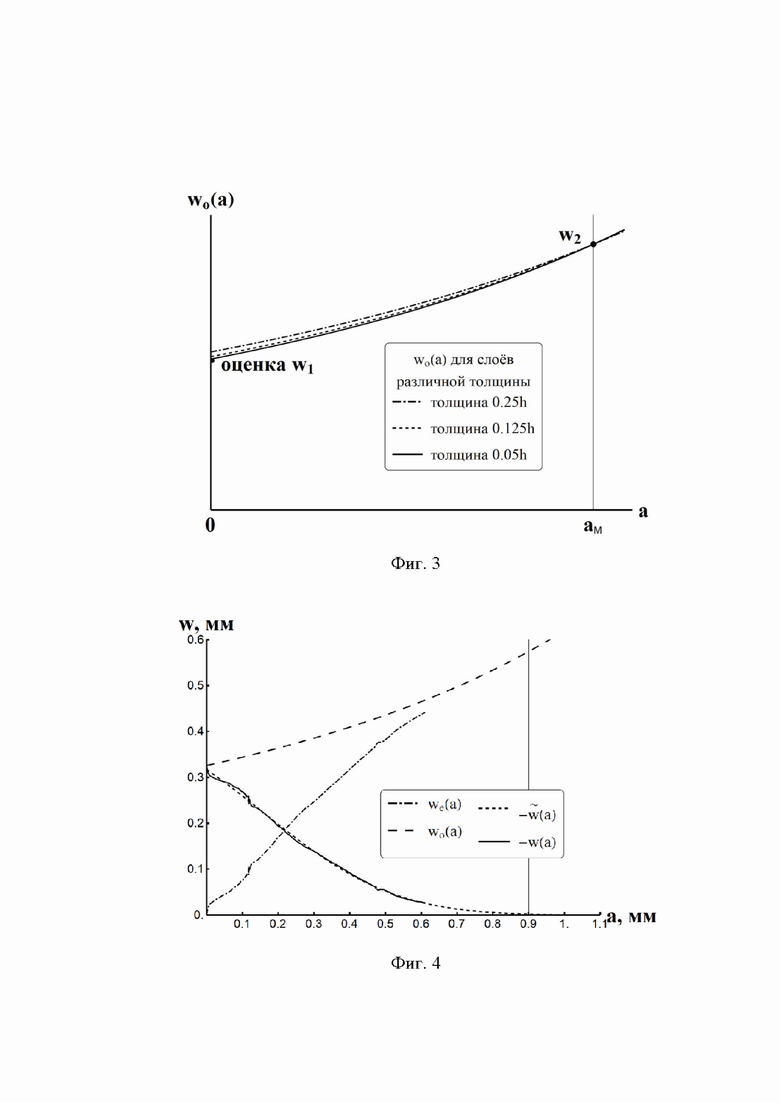
На фиг. 2 схематически приведены все зависимости в (1), а на фиг. 3 дана оценка точности приближенного выражения в (3).
Если зависимость w(а) плавно стремится к нулю при возрастании а, то максимальная толщина снятого слоя ам превышает толщину слоя собственных деформаций, т.е. удален весь слой. Зависимость w(а) аппроксимируется гладкой функцией  на отрезке a∈[0,aм] и продолжается
на отрезке a∈[0,aм] и продолжается 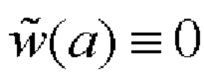 , а≥ам.
, а≥ам.
Если же эта зависимость имеет негладкость в точке а=ам, соответствующей максимальной толщине снятого слоя, это означает, что в полосе остаются собственные деформации. В этом случае зависимость w(а) следует аппроксимировать гладкой функцией  , плавно стремящейся к некоторой величине
, плавно стремящейся к некоторой величине 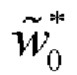 при а>ам. Итоговую аппроксимацию необходимо записать как
при а>ам. Итоговую аппроксимацию необходимо записать как  .
.
Далее по гладкой аппроксимации 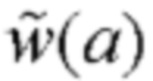 определяется распределение собственных деформаций по формуле
определяется распределение собственных деформаций по формуле

где штрих означает производную.
По реконструированному профилю собственных деформаций определяется профиль остаточных напряжений

удовлетворяющий уравнениям равновесия, где Е - модуль Юнга, v -коэффициент Пуассона.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
На фиг. 1 приведена схема симметричного распределения собственных деформаций по толщине полоски.
Фиг. 2 - иллюстрация вида зависимостей прогиба полосы от толщины удаленного слоя для пластин с двухсторонним и односторонними слоями собственных деформаций.
Фиг. 3 - оценка точности приближения по формулам (2)-(3).
Фиг. 4 - пример сведения экспериментальной зависимости прогиба от толщины стравленного слоя при двусторонней обработке к зависимости соответствующей односторонней обработки и ее аппроксимация гладкой функцией.
Фиг. 5 - реконструированное распределение собственных деформаций для половины толщины полосы для примера из фиг. 4.
Фиг. 6 - реконструированное распределение остаточных напряжений для половины толщины полосы для примера из фиг. 4.
Применение изобретения иллюстрируется примером. Исследовалась полоса длиной 58 мм и шириной 14,5 мм, вырезанная из пластины титанового сплава ВТ6 толщиной 3,45 мм, подвергнутая двусторонней лазерной проковке. Послойное удаление материала реализовано электрохимическим травлением на установке Меркулон Тензор-3. На фиг. 4 приведена экспериментальная зависимость we(а), а также зависимости wo(a) и w(a), рассчитанные по (1)-(3). Там же приведена гладкая аппроксимация зависимости w(а) функцией

где с1=0,228 мм, с2=-0,223 мм, с3=0,405 мм, с4=-0,394, и показано, что глубина травления ам=0,61 мм оказалась недостаточна для выявления слоя собственных деформаций толщиной около 0,9 мм.
На фиг. 5 и 6 показаны профили собственных деформаций и остаточных напряжений, реконструированные по формулам (4), (5). Следует обратить внимание на то, что применение к 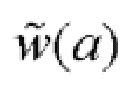 формулы Биргера [2]
формулы Биргера [2]

дает профиль остаточных напряжений, не удовлетворяющий уравнениям равновесия. Распределение (6) отличается от равновесного (5) на константу.
Изобретение позволяет найти не только профиль остаточных напряжений, но и профиль собственных (неупругих) деформаций, который, в отличие от профиля остаточных напряжений, удобно внедрять в конечно-элементный расчет поверхностно обработанных деталей сложной формы.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения распределения остаточных напряжений по толщине металлоизделия с высокими поверхностными градиентами | 2024 |
|
RU2834607C1 |
| СПОСОБ КОНТРОЛЯ ДРОБЕСТРУЙНОГО УПРОЧНЕНИЯ ДЕТАЛЕЙ | 2017 |
|
RU2661163C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДЕЛА ТЕКУЧЕСТИ МАТЕРИАЛА ПРИ ДРОБЕСТРУЙНОЙ ОБРАБОТКЕ | 2020 |
|
RU2746851C1 |
| СПОСОБ ФОРМИРОВАНИЯ СЖИМАЮЩИХ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ ПРИ ДРОБЕСТРУЙНОЙ ОБРАБОТКЕ ДЕТАЛЕЙ | 2019 |
|
RU2704341C1 |
| Способ определения остаточных напряжений в ребре на жестком основании | 2022 |
|
RU2797771C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ | 2007 |
|
RU2354952C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РАСПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ ПО СЕЧЕНИЮ СТЕНКИ ТРУБЫ (ВАРИАНТЫ) | 2019 |
|
RU2738997C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ | 1996 |
|
RU2121666C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ | 2011 |
|
RU2455622C1 |
| Способ сохранения инфрамаммарной складки при выполнении подкожной или кожесохраняющей радикальной мастэктомии | 2023 |
|
RU2830291C1 |

Изобретение относится к разрушающим способам реконструкции профиля остаточных напряжений по толщине пластины, основанным на послойном удалении материала с поверхности вырезанной из нее полоски и измерении ее прогиба. Указанная пластина является упругой пластиной с симметричным распределением по толщине остаточных напряжений, наведенных двухсторонней поверхностной обработкой. Способ включает постепенное удаление материала с одной из плоскостей полоски с использованием установки, в которой реализован метод Давиденкова - Биргера с сопутствующим измерением ее прогиба и определения по этим данным профилей собственных деформаций и остаточных напряжений. Технический результат - реконструкция симметричного профиля остаточных напряжений в пластине с использованием данных прогиба полоски при одностороннем стравливании материала без ее продольного разрезания. 6 ил.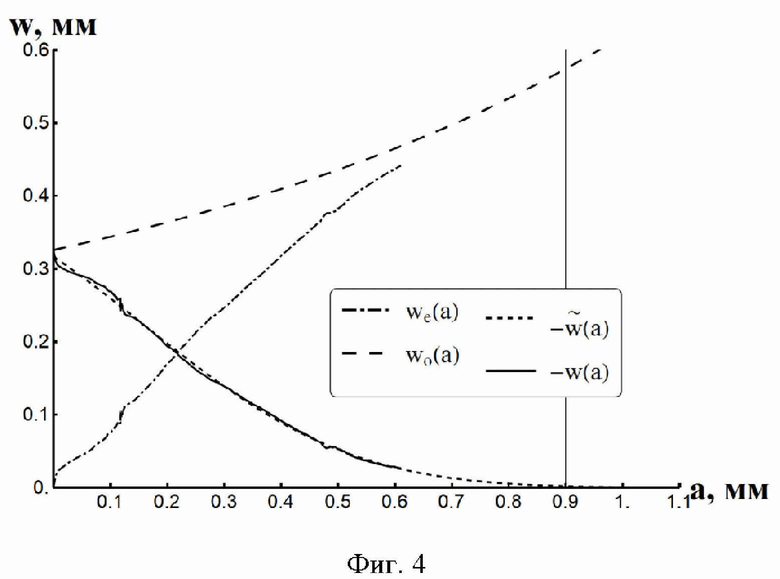
Способ определения симметричного распределения остаточных напряжений по толщине пластины, при котором экспериментально определяют зависимость изменения прогиба полосы, вырезанной из пластины с двухсторонним поверхностным слоем собственных деформаций, от толщины слоя материала, удаленного с одной из поверхностей полосы при постепенном удалении материала и измерении прогиба полосы, отличающийся тем, что профили собственных деформаций и остаточных напряжений вычисляют по этим данным с использованием реконструктивных формул

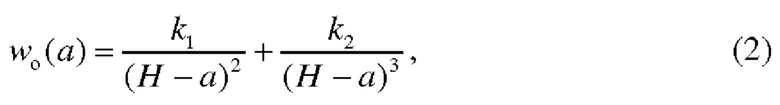
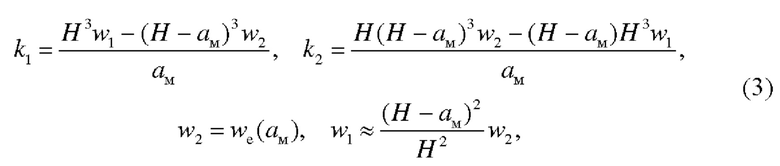

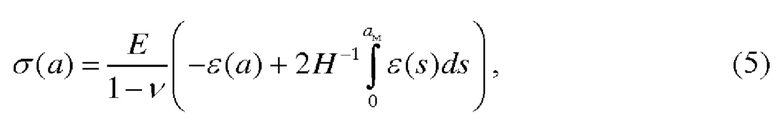
где  - экспериментальная зависимость изменения прогиба полосы, вырезанной из пластины с двухсторонним поверхностным слоем собственных деформаций, от
- экспериментальная зависимость изменения прогиба полосы, вырезанной из пластины с двухсторонним поверхностным слоем собственных деформаций, от  - толщины слоя материала, удаленного с одной из поверхностей полосы при постепенном удалении материала,
- толщины слоя материала, удаленного с одной из поверхностей полосы при постепенном удалении материала,  - аналогичная теоретическая зависимость для полосы с поверхностным слоем собственных деформаций со стороны травления,
- аналогичная теоретическая зависимость для полосы с поверхностным слоем собственных деформаций со стороны травления, 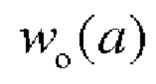 - теоретическая оценка аналогичной зависимости для полосы с поверхностным слоем собственных деформаций с противоположной стороны,
- теоретическая оценка аналогичной зависимости для полосы с поверхностным слоем собственных деформаций с противоположной стороны,  - значение прогиба
- значение прогиба  , соответствующее максимальной толщине удаленного слоя
, соответствующее максимальной толщине удаленного слоя 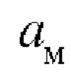 , которая должна превышать толщину слоя собственных деформаций,
, которая должна превышать толщину слоя собственных деформаций,  - аппроксимация зависимости
- аппроксимация зависимости 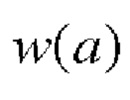 гладкой функцией,
гладкой функцией,  - ее предельное значение при
- ее предельное значение при  ,
,  и
и  - реконструированные профили собственных деформаций и остаточных напряжений по координате
- реконструированные профили собственных деформаций и остаточных напряжений по координате 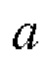 , изменяющейся по толщине пластины, Н, L - толщина и длина полосы, Е - модуль Юнга,
, изменяющейся по толщине пластины, Н, L - толщина и длина полосы, Е - модуль Юнга, 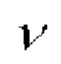 - коэффициент Пуассона, штрих означает производную, s - переменную интегрирования.
- коэффициент Пуассона, штрих означает производную, s - переменную интегрирования.
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ | 1996 |
|
RU2121666C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ В ДЕТАЛИ | 2012 |
|
RU2600518C2 |
| US 11609169 B2, 21.03.2023. | |||
Авторы
Даты
2024-05-06—Публикация
2023-10-13—Подача