Изобретение относится к области бортового приборостроения и автоматики, может быть использовано для решения пилотажно-навигационных задач при автономном управлении наземными, плавающими, летательными, баллистическими и космическими аппаратами на основе результатов обработки инерциальной информации.
В практике управления различными судами (воздушными, плавающими) и аппаратами (наземными, баллистическими, космическими) при решении задач навигации подвижных объектов (ПО) предпочтение отдают способам автономной навигации, реализующим бесплатформенные технологии. [1, 2].
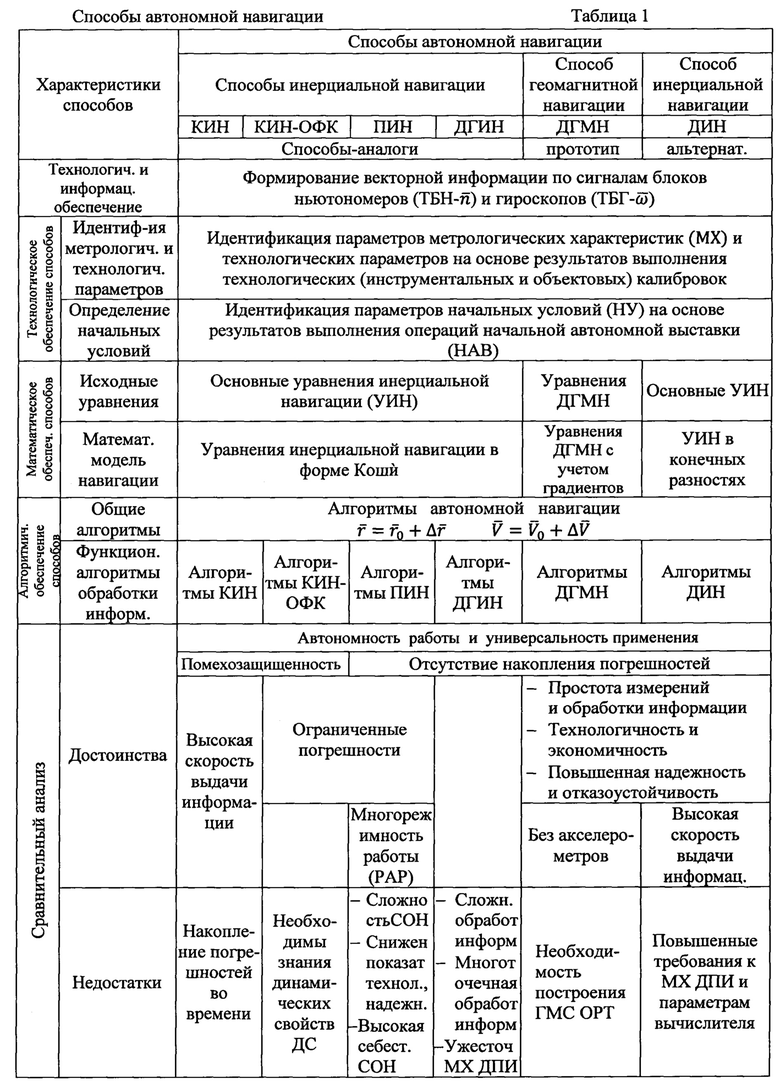
Чаще всего такие способы предполагают получение и обработку инерциональной информации, а также информации о геофизических полях (табл. 1).
Сравнительная характеристика существующих способов (аналогов, прототипа) и предлагаемого способа (альтернативы) представлена в табл.1. Из анализа табл.1 видно, что все способы бесплатформенной автономной навигации имеют общее техническое (основной состав датчиков первичной информации - ДПИ), информационное (структуру первичной приборной информации - ППИ), метрологическое, технологическое обеспечения. Отличительные особенности сравниваемых способов проявляются только в математическом и программно-алгоритмическом обеспечении способов, что связано с характеристикой способов обработки информации. Общие алгоритмы обработки информации для всех способов бесплатформенной автономной навигации (БАН) сводятся к реализации векторных уравнений навигации (уравнений навигационных треугольников позиционирования и скоростей):

где  - начальный радиус-вектор точки старта ПО,
- начальный радиус-вектор точки старта ПО,
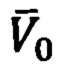 - вектор начальной скорости движения ПО в точке старта,
- вектор начальной скорости движения ПО в точке старта,
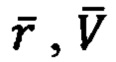 - радиус-вектор точки текущего местоположения и вектор текущей скорости ПО,
- радиус-вектор точки текущего местоположения и вектор текущей скорости ПО,
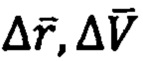 - вариации векторов
- вариации векторов 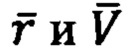 на каждом шаге вычислений (конечные разности векторов).
на каждом шаге вычислений (конечные разности векторов).
Сущность всех способов БАН (в соответствии с выражениями (1)) сводится к получению ППИ 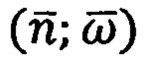 с помощью векторных ДЛИ (ньютономеров и гироскопов) и последующей ее обработке с целью последовательного решения трех задач:
с помощью векторных ДЛИ (ньютономеров и гироскопов) и последующей ее обработке с целью последовательного решения трех задач:
- задачи автономной начальной выставки (НАВ), т.е. определения векторов 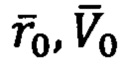 в точке старта ПО,
в точке старта ПО,
- задачи определения вариаций векторов 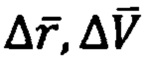 путем текущей обработки ППИ,
путем текущей обработки ППИ,
- задачи определения конечных векторов 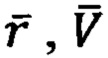 для текущей точки местоположения ПО в околоземном пространстве.
для текущей точки местоположения ПО в околоземном пространстве.
Приемы решения задачи НАВ являются общими для всех способов БАН. Приемы же решения второй и третьей задач индивидуальны для каждого способа и отражают сущность и отличительные особенности соответствующего способа БАН. Следовательно, анализируемые способы БАН в основном отличаются способами обработки ППИ.
Известен способ двумерной инерциальной навигации ПО на плоской горизонтальной поверхности Земли без учета факторов сферичности Земли и ее вращения. Способ предложен немецким инженером Р. Вуссовым в 1905 г. и запатентован [1-3]. Сущность способа инерциальной навигации на горизонтальной плоскости по Р. Вуссову заключается в кинематическом инерциальном счислении пройденного ПО пути, которое выполняется по сигналам 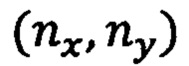 двух ньютономеров с горизонтально ориентированными осями чувствительностей X, Y с использованием интегральных функциональных приемов без учета вращения ПО по курсу в горизонтальной плоскости:
двух ньютономеров с горизонтально ориентированными осями чувствительностей X, Y с использованием интегральных функциональных приемов без учета вращения ПО по курсу в горизонтальной плоскости:

где 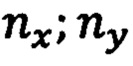 - сигналы горизонтальных ньютономеров, соответствующие проекциям на их оси чувствительностей вектора кажущегося ускорения
- сигналы горизонтальных ньютономеров, соответствующие проекциям на их оси чувствительностей вектора кажущегося ускорения

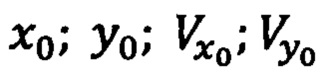 - начальные условия, характеризующие координаты точки старта ПО и компоненты его начальной скорости:
- начальные условия, характеризующие координаты точки старта ПО и компоненты его начальной скорости:

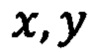 - координаты точки текущего местоположения ПО на горизонтальной плоскости,
- координаты точки текущего местоположения ПО на горизонтальной плоскости,
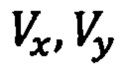 - проекции вектора текущей скорости ПО на оси горизонтального координатного базиса OXY.
- проекции вектора текущей скорости ПО на оси горизонтального координатного базиса OXY.
Оси координатного базиса отсчета OXY могут быть ориентированы по направлениям горизонтальных осей географического трехгранника q=NHE или ортодромического трехгранника. Предполагается, что в процессе кинематического инерциального счисления пройденного ПО пути оси чувствительностей ньютономеров (ОХ и OY) всегда лежат в горизонтальной плоскости и совпадают с соответствующими осями выбранного отсчетного базиса (географического или ортодромического). С учетом принятых условий получается самый простой вариант способа кинематической инерциальной навигации (КИН) на горизонтальной плоскости (табл.1), для которого абсолютное ускорение 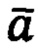 ПО всегда совпадает с кажущимся ускорением
ПО всегда совпадает с кажущимся ускорением  регистрируемым ньютономерами:
регистрируемым ньютономерами:

Условия (6) дают основание к обоснованию работоспособности функциональных приемов (2)-(5) двумерной инерциальной навигации ПО на горизонтальной плоскости с учетом принятых условий.
Недостатки способа двумерной инерциальной навигации в горизонтальной плоскости (по Р. Вуссову) заключаются в следующем:
- на практике способ может быть реализован в течение ограниченного промежутка времени (не более 10-15 минут) только в пределах малых участков Земли (не более 100 км) принимаемых за горизонтальные плоскости без учета фактора кривизны поверхности Земли и ее вращения 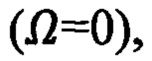
- практически способ не может быть использован применительно к реальному трехмерному околоземному пространству из-за несовершенства функциональных приемов обработки инерциальной информации, не учитывающих пространственный характер движения ПО 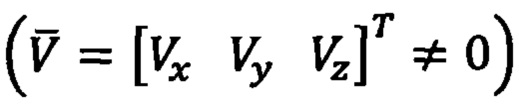 , а также факторы вращения Земли
, а также факторы вращения Земли 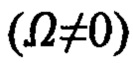 и кривизны ее поверхности,
и кривизны ее поверхности,
- способ обладает низкой точностью из-за проявления методических погрешностей, связанных с неучетом факторов кривизны поверхности Земли, ее вращением, пространственным характером движения ПО, а также из-за накопления вычислительных погрешностей, обусловленных процессом интегрирования сигналов ньютономеров, содержащих полезную информацию и инструментальные ошибки.
С учетом отмеченных недостатков способ КИН по Вуссову Р. не получил широкого применения на практике и может быть использован только для решения частных задач автономной навигации ПО с учетом ограничений в области времени, пространства и допустимых ошибок. В настоящее время способ двумерной навигации по Р. Вуссову специалисты в области автономного управления ПО используют в демонстрационных и учебных целях, а также рассматривают его как научно-методический прием для разработки и совершенствования способов трехмерной инерциальной навигации ПО в околоземном пространстве.
Известны варианты способов пространственной автономной навигации инерциальной (ПАНИ) ПО в трехмерном околоземном пространстве, объединенных в единую группу способов трехмерной инерциальной навигации [1,2].
Способы пространственной трехмерной инерциальной навигации ПО в околоземном пространстве основаны на принципе кинематического счисления пройденного пути в трехмерном пространстве. Впервые задача пространственной навигации ПО в околоземном пространстве с учетом несферичности и вращения Земли, а также поля тяжести Земли (ПТЗ) была поставлена и решена советским ученым, профессором Московского энергетического института Л. И. Ткачевым [3].
В основу формирования ядра математической модели кинематической инерциальной навигации (КИН) для получения функциональных приемов обработки инерциальной информации в способах ПАНИ положены два векторных уравнения механики твердого тела [1-4]:
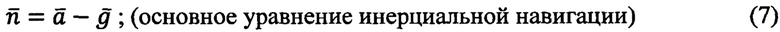
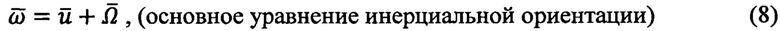
где  - векторы кажущегося и абсолютного ускорений ПО,
- векторы кажущегося и абсолютного ускорений ПО, 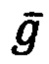 - вектор удельной силы тяжести,
- вектор удельной силы тяжести,
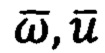 - векторы абсолютной и относительной угловых скоростей вращения ПО в инерциальном
- векторы абсолютной и относительной угловых скоростей вращения ПО в инерциальном 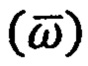 и околоземном
и околоземном 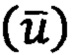 пространстве,
пространстве,
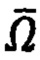 - вектор угловой скорости собственного суточного вращения Земли, Ω = 7,292116⋅10-5с-1.
- вектор угловой скорости собственного суточного вращения Земли, Ω = 7,292116⋅10-5с-1.
Функциональные приемы обработки инерциальной и гравиметрической информации в способах ПАНИ учитывают множество факторов:
- геометрический (геометрическую форму фигуры Земли),
- кинематический (вращение Земли, Ω≠0),
- физический (характеристику формирования поля тяжести Земли (ПТЗ) в околоземном пространстве),
- технический (учитывающий схему построения (ортогональную и неортогональную) блоков инерциальных измерителей - гироскопов и ньютономеров),
- метрологический (учитывающий реальные, а не расчетные метрологические характеристики инерциальных измерителей),
- технологический (характеризующий индивидуальные технологические свойства измерителей).
Варианты способов ПАНИ отличаются друг от друга прежде всего функциональными алгоритмами обработки информации, а также способами описания геометрии и кинематики вращательного движения ПО [2]. Из механики твердого тела и гравиметрии известно, что
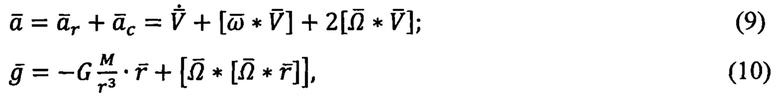
где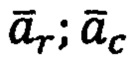 - векторы относительного и кориолисова ускорений,
- векторы относительного и кориолисова ускорений, 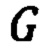 - всемирная гравитационная постоянная,
- всемирная гравитационная постоянная,
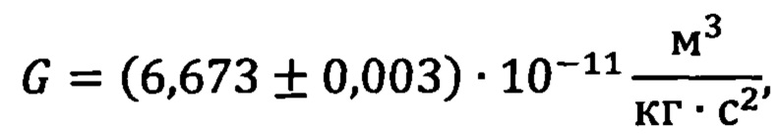
М - масса Земли, М = 5,924⋅1024 кг.
Путем подстановки выражений (4), (5) в основное уравнение инерциальной навигации (2) и соответствующего преобразования получают общие уравнения инерциальной навигации в форме Коши (табл.1):
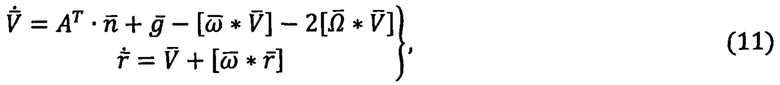
где 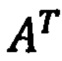 - транспонированная матрица ориентации ПО в околоземном пространстве. Из анализа общих уравнений инерциальной навигации (11) видно, что задача пространственной инерциальной навигации ПО в околоземном пространстве тесно связана с частными задачами:
- транспонированная матрица ориентации ПО в околоземном пространстве. Из анализа общих уравнений инерциальной навигации (11) видно, что задача пространственной инерциальной навигации ПО в околоземном пространстве тесно связана с частными задачами:
- с задачей ориентации ПО 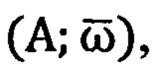
- с задачей гравиметрии 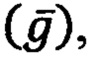
- с задачей инерциальных измерений 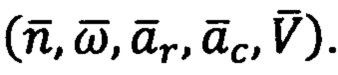
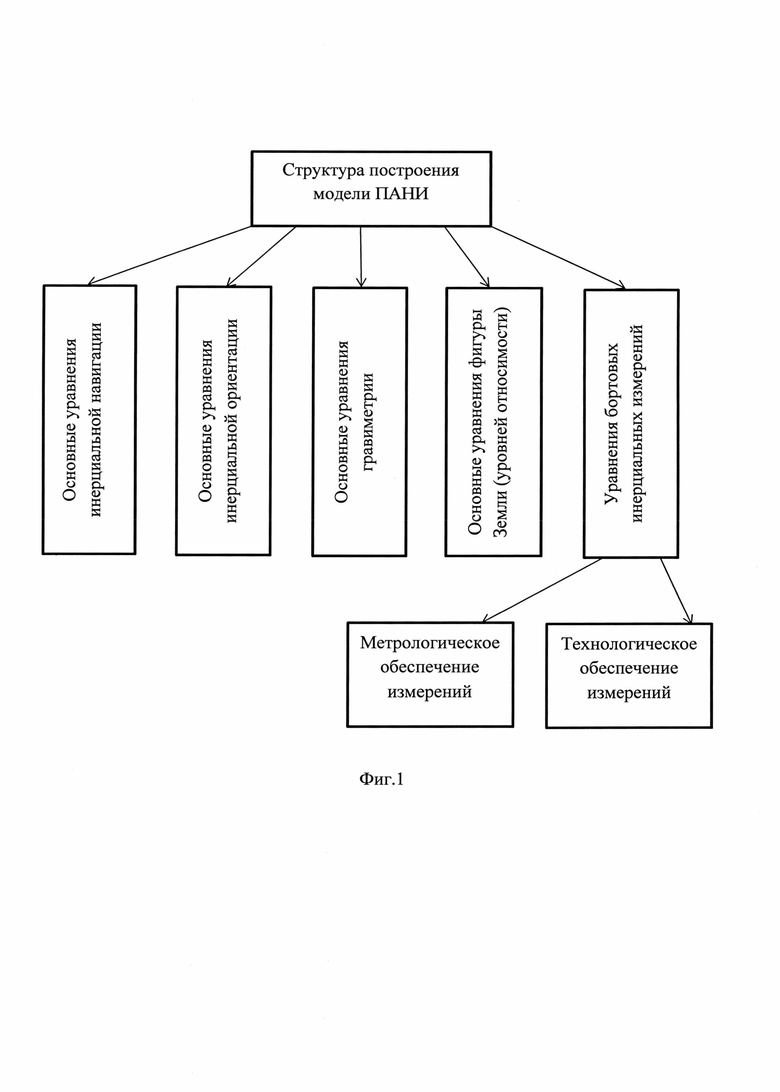
Этот факт означает, что структура математической модели пространственной инерциальной навигации ПО должна быть построена на основе расширения общих уравнений инерциальной навигации (Фиг. 1).
Общие приемы пространственной инерциальной навигации могут быть получены путем интегрирования по времени уравнений (11):
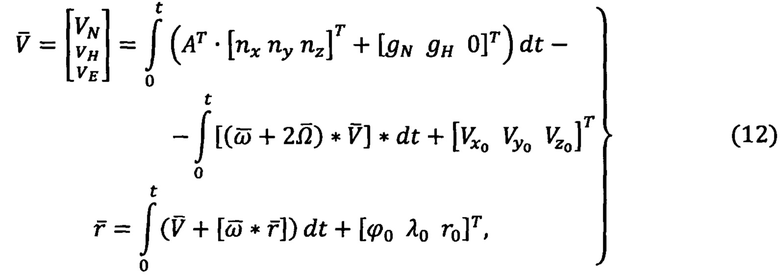
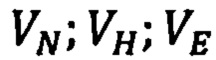 - северная, вертикальная и восточная составляющие вектора относительной скорости
- северная, вертикальная и восточная составляющие вектора относительной скорости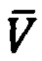 ПО,
ПО,
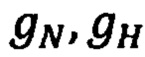 - северная и вертикальная составляющие вектора удельной силы тяжести
- северная и вертикальная составляющие вектора удельной силы тяжести 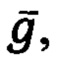
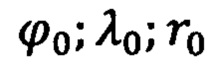 - полярные координаты точки старта ПО (начальные значения географической широты, долготы и модуля радиуса-вектора).
- полярные координаты точки старта ПО (начальные значения географической широты, долготы и модуля радиуса-вектора).
Основные уравнения инерциальной навигации (11) и, соответственно, общие алгоритмы пространственной инерциальной навигации ПО (12) могут быть представлены в различных формах в зависимости от того, в терминах каких параметров решают задачу инерциальной ориентации и какую конкретно формулу используют для решения задачи гравиметрии (Фиг. 1).
При решении задачи инерциальной ориентации ПО на практике обычно используют три варианта параметров ориентации [1,2]:
- трехмерные параметры ориентации в виде эйлеровых углов (например, углов Эйлера-Крылова: ψ - курса, ϑ - тангажа (дифферента), γ - крена (вращения)),
- четырехмерные параметры ориентации в виде параметров Родрига-Гамильтона 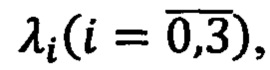 применяемых для формирования кватернионов вращения ПО:
применяемых для формирования кватернионов вращения ПО:

- девятимерные параметры ориентации в виде направляющих косинусов 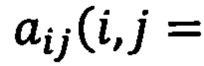
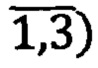 матриц ориентации ПО:
матриц ориентации ПО:

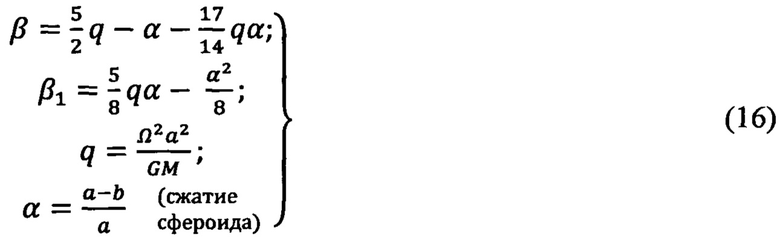
Для решения прикладных задач геофизики и геологоразведки часто используют основное уравнение гравиметрии, принятое в 1967 г. на XIV Генеральной ассамблее Международного геодезического и геофизического союза в качестве международной стандартной формулы для вычисления удельной нормальной силы тяжести у на поверхности земного референц-эллипсоида:
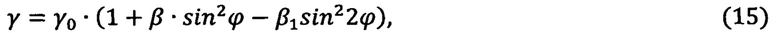
где γ0 - ускорение силы тяжести на экваторе Земли,
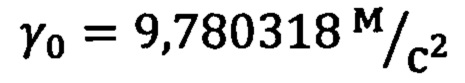
ϕ - географическая широта,
β, β1 - коэффициенты.
Причем
Численные значения параметров основного уравнения гравиметрии (стандарт WGS-84):

С учетом значений параметров (17) основное уравнение (15) приобретает форму численного уравнения.
Стандартное основное уравнение гравиметрии после приведения его к осям географического трехгранника q=NHE позволяет определить северную (gN) и вертикальную (qн) составляющие вектора  [5]:
[5]:
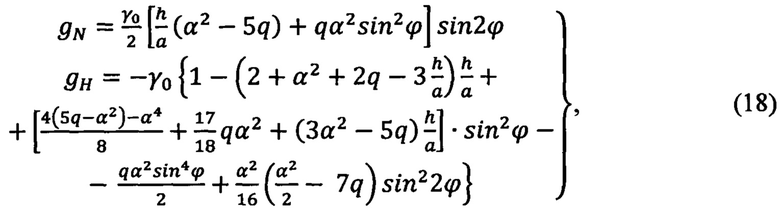
где h - высота текущей точки местоположения ПО в околоземном пространстве, отсчитанная по нормали к поверхности референц-эллипсоида. Кроме основного уравнения гравиметрии в стандартной форме (18) на практике могут использоваться и другие формы нестандартных основных уравнений гравиметрии, которые в разной степени точности позволяют решать задачу описания ПТЗ.
Модели схемо-технического, метрологического и технологического обеспечений решения задачи инерциальной навигации ПО в околоземном пространстве достаточно обстоятельно разработаны в научно-технической и патентной литературе [6]. Объединение в одну общую систему частных уравнений:
- основных уравнений инерциальной навигации (11),
- основных уравнений инерциальной ориентации с использованием параметров 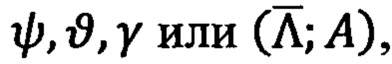
- основного уравнения гравиметрии (15) - (18),
а также моделей технического, метрологического и технологического обеспечений решения задачи КИН позволяет сформировать обобщенную расширенную модель ПАНИ (табл. 1, фиг. 1). Эту модель ПАНИ в разных формах используют специалисты в области управления ПО (морскими, наземными, летательными, баллистическими, космическими) в качестве основы для разработки различных вариантов способов решения задачи ПАНИ (табл. 1).
Общим недостатком всех способов решения ПАНИ ПО в околоземном пространстве является низкая точность решения задачи, обусловленная процессом накопления во времени погрешностей, что в свою очередь, связано с использованием интегральных алгоритмов приемов обработки информации в способах КИН (12). Оценку накапливаемых погрешностей КИН можно получить из уравнений (12) - (18) с учетом проявления первичных ошибок измерений и вычислений. Этот факт послужил толчком к поиску и разработке во второй половине XX столетия способов усовершенствования вариантов решения задачи ПАНИ путем введения дополнительной обработки ППИ. При этом приемы дополнительной обработки ППИ строят на основе следующих принципов (принципов ОФК):
- теории оценивания и наблюдающих устройств,
- теории фильтрации сигналов,
- теории коррекции первичной и промежуточной информации.
Способы ПАНИ нашли широкое практическое применение в морском флоте, авиации, а также при управлении наземными объектами и объектами ракетно-космической техники начиная с середины XX столетия.
Известна группа способов решения задачи трехмерной инерциальной навигации ПО в околоземном пространстве с учетом введения дополнительных операций оценивания, фильтрации, коррекции (ОФК) информации [1,2,7].
Все способы этой группы (ПАНИ-ОФК) отличаются тем, что математическое описание схемы решения задачи пространственной инерциальной навигации ПО расширено за счет того, что основные уравнения инерциальной навигации, ориентации и гравиметрии (12)-(18) дополнены уравнениями оценивания сигналов и наблюдающих устройств, уравнениями фильтрации и коррекции информации. На практике широкое распространение получили линейные методы обработки навигационной информации, которые требуют соответствующей линеаризации результатов как навигационных измерений, так и моделей погрешностей ДПИ, входящих в состав ИНС.
Расширение уравнений ПАНИ основано на том, что с целью повышения точности решения задачи инерциальной навигации в околоземном пространстве следует обеспечить не только обработку ППИ по выражениям (12)-(18) идеальной работы инерциальной навигационной системы (ИНС), но и обработку информации с учетом проявления реальных помех, погрешностей измерений и возмущений:

где 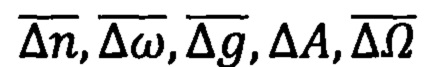 - векторы ошибок, характеризующие погрешности измерений и вычислений, соответственно. Путем подстановки выражений (19) в основные уравнения инерциальной навигации (11) с учетом уравнений ориентации и гравиметрии (15)-(18) получают расширенную модель инерциальной навигационной системы (ИНС) в форме
- векторы ошибок, характеризующие погрешности измерений и вычислений, соответственно. Путем подстановки выражений (19) в основные уравнения инерциальной навигации (11) с учетом уравнений ориентации и гравиметрии (15)-(18) получают расширенную модель инерциальной навигационной системы (ИНС) в форме  [1,2,7,8]:
[1,2,7,8]:

где 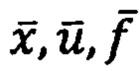 - векторы состояния (n * 1) динамической системы (ДС), ее управления (m * 1) и возмущения (r * 1), соответственно,
- векторы состояния (n * 1) динамической системы (ДС), ее управления (m * 1) и возмущения (r * 1), соответственно,
А - собственная матрица ДС (n * n),
В, С - матрицы коэффициентов эффективности управлений (m * n) и возмущений (r * n) ДС, соответственно.
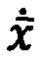 -вектор производных по времени от составляющих вектора
-вектор производных по времени от составляющих вектора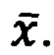
В простейшем случае в соответствии с уравнением (11) вектор состояния ИНС как динамической системы (ДС) представляют в виде четырехмерного вектора (для КИН по Р. Вуссову):

В общем случае в соответствии с моделью (20) работу ИНС представляют как динамический процесс -го порядка с n-мерным вектором состояния 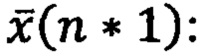
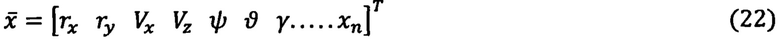
Для наблюдения за этим динамическим процессом используют различные наблюдающие устройства (НУ), в состав которых входят датчики первичной информации (ДЛИ), фильтры и вычислительные устройства в виде микроконтроллеров (МК). Текущее состояние НУ может быть описано с помощью математической модели наблюдений [1,2,7]:

где 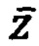 - вектор состояния НУ (вектор измерения, наблюдения (S * 1) (S ≤ n),
- вектор состояния НУ (вектор измерения, наблюдения (S * 1) (S ≤ n),
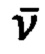 - вектор шумов и помех измерений (z * 1),
- вектор шумов и помех измерений (z * 1),
D - матрица измерений (наблюдений) системы (S * n).
В соответствии с выражениями (19) для получения значений измеряемых 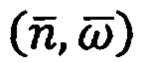 и вычисляемых
и вычисляемых  векторов и параметров, приближенным к их действительным значениям, необходимо решать две задачи:
векторов и параметров, приближенным к их действительным значениям, необходимо решать две задачи:
- задачу оценивания самих переменных величин (измеряемых - 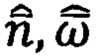 и вычисляемых -
и вычисляемых - 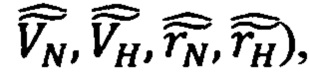
- задачу оценивания погрешностей определения этих переменных (погрешностей измерений - 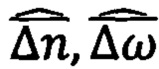 и погрешностей вычислений -
и погрешностей вычислений - 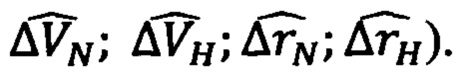
С этой целью необходимо сформировать две модели:
- модель «идеальной» работы ИНС,
- модель погрешностей ИНС.
Первую модель получают на основе уравнений (11), (15)-(18), если в них подставить выражения (19) и предположить отсутствие погрешностей измерений и вычислений 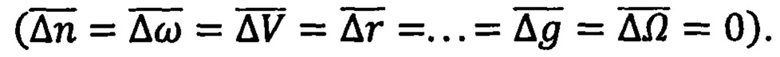
В соответствии с уравнениями ДС (20), (21) прием оценивания вектора состояния ДС 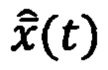 строят на основе решения уравнения оценивания [7]:
строят на основе решения уравнения оценивания [7]:

где 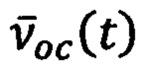 - вектор сигналов отрицательной обратной связи (цепи коррекции)
- вектор сигналов отрицательной обратной связи (цепи коррекции) 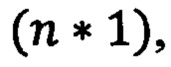
K - матрица коэффициентов усиления цепи коррекции 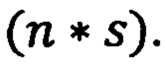
Приемы оценивания вектора состояния ДС 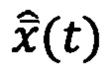 на основе статистических подходов формируют и используют в способах ПАНИ-ОФК с учетом заданных априорно вероятностных характеристик измерений ДЛИ.
на основе статистических подходов формируют и используют в способах ПАНИ-ОФК с учетом заданных априорно вероятностных характеристик измерений ДЛИ.
Вторую модель (уравнения погрешностей ИНС) формируют на основе линеаризации уравнений (11), (15), (18) с учетом подстановки в них выражений (19) и последующего выделения уравнений в вариациях. При этом под вектором оценок погрешностей состояния ДС понимают разность векторов

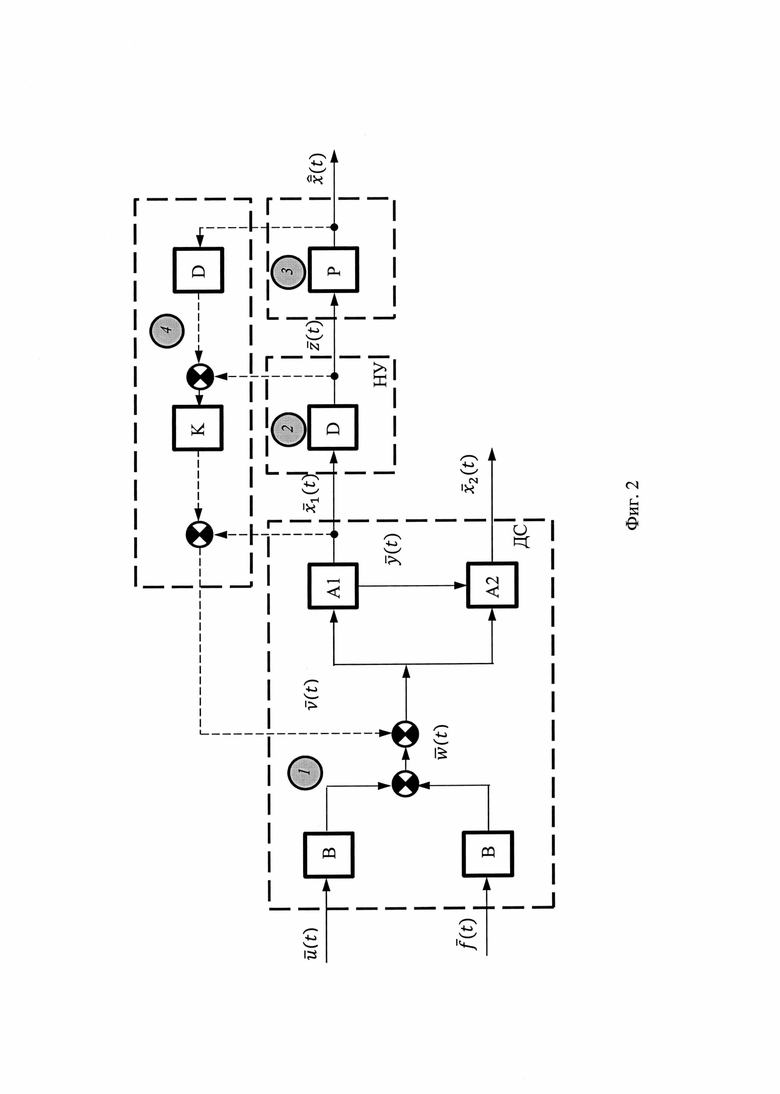
Схема взаимодействия ДС (ИНС) с НУ для способов ПАНИ-ОФК представлена на фиг. 2. В качестве наблюдающих устройств могут выступать различные фильтры (в частности, дискретные фильтры Винера, Калмана, Бьюси и др.). К настоящему времени различные модификации фильтров Калмана (ФК) широко применяют в навигационной практике [1,2,7]. Эти многомерные фильтры обеспечивают решение задачи оптимального и субоптимального оценивания параметров состояния навигационных систем с минимальными погрешностями. Задачей оптимальной фильтрации сигналов в постановке Калмана является отыскание по измерениям векторного случайного процесса 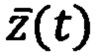 оценки
оценки 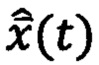 вектора состояния ДС
вектора состояния ДС 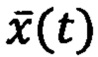 (задача восстановления информации о векторе
(задача восстановления информации о векторе 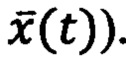 При этом оценка производится наблюдающим устройством (многомерным фильтром), представляющим собой динамическую систему, на вход которой поступают доступные сигналы измерений в виде вектора наблюдений
При этом оценка производится наблюдающим устройством (многомерным фильтром), представляющим собой динамическую систему, на вход которой поступают доступные сигналы измерений в виде вектора наблюдений 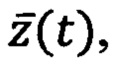 а выходом является оценка вектора состояния
а выходом является оценка вектора состояния 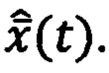
В конечном счете на основе оценки погрешности вектора состояния ДС 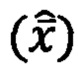 строят процесс коррекции (управления) ИНС (фигура 2):
строят процесс коррекции (управления) ИНС (фигура 2):

Основным недостатком всех способов решения задачи ПАНИ с использованием операций оценивания, фильтрации и коррекции (ОФК) является сложность приемов обработки информации:
- уравнений «идеальной работы» ИНС,
- приемов оценивания вектора состояния ИНС и вектора ее погрешностей,
- приемов оценки свойств полной наблюдаемости и полной управляемости (коррекции) ИНС,
- приемов коррекции ИНС.
Сложность приемов ОФК в способах решения задачи пространственной инерциальной навигации ПО в околоземном пространстве, в свою очередь, требует использования сверхбыстродействующих (более нескольких миллионов операций в секунду), сверхпроизводительных (более одного Мбит/сек), высокоразрядных (с длиной разрядной сетки 32 бит и больше), многоядерных микропроцессорных систем с организацией параллельных вычислений. Игнорирование этих ограничений может привести на практике к проявлению неустойчивых процессов обработки информациии накоплению больших погрешностей вычислений. Другими словами, вместо процесса накопления методических погрешностей, вызванных интегрированием первичных погрешностей измерений 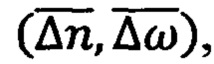 в соответствии с интегральными алгоритмами (7) в способах ПАНИ-ОФК может наблюдаться процесс накопления вычислительных погрешностей из-за реализации в МК неустойчивых процессов обработки информации.
в соответствии с интегральными алгоритмами (7) в способах ПАНИ-ОФК может наблюдаться процесс накопления вычислительных погрешностей из-за реализации в МК неустойчивых процессов обработки информации.
С другой стороны, способы ПАНИ-ОФК позволяют снизить уровень погрешностей и скорость их нарастания во времени, но не исключают само свойство увеличения погрешностей во времени.
Известна группа способов решения задачи пространственной инерциальной навигации ПО в околоземном пространстве на основе использования принципов
- комплексирования средств навигации,
- коррекции ИНС путем сравнения выходных сигналов ИНС с выходными сигналами эталонных навигационных систем.
Способы этой группы обеспечивают реализацию позиционно-инерциальной навигации (ПИН), отличающейся тем, что погрешности навигации при реализации этого способа не накапливаются во времени и ограничены по модулю соответствующим характером (чаще всего колебательным) изменения во времени (табл. 1). Ограничения роста погрешностей инерциальной навигации по модулю во времени достигают путем введения в интегральные алгоритмы навигации (12) корректирующих членов, обеспечивающих коррекцию работы ИНС в соответствии с принципом отрицательной обратной связи, известным из теории автоматического регулирования. Для описания способа ПИН схема, представленная на фиг. 2, остается справедливой с учетом дополнения к ИНС с НУ эталонной навигационной системы (ЭНУ) (на фиг. 2 не показана).
Вектор отрицательной обратной связи (ООС) 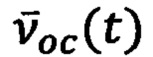 формируют на основе сравнения вектора оценок состояния ДС (ИНС)
формируют на основе сравнения вектора оценок состояния ДС (ИНС) 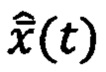 с соответствующим вектором состояния эталонной навигационной системы
с соответствующим вектором состояния эталонной навигационной системы 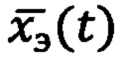 и вычисляют по формуле (вместо формулы (25)):
и вычисляют по формуле (вместо формулы (25)):

Коэффициенты матрицы ООС К выбирают исходя из условия удовлетворения заданному критерию качества по точности, быстродействию, устойчивости интегрированной навигационной системы в замкнутом состоянии.
В частности, коэффициенты матрицы ООС К выбирают такими, чтобы настроить замкнутую систему навигации на период М. Шулера (Т « 84,4 мин), обеспечивающий системе свойство динамической невозмущаемости относительно действия ускорений ПО. При такой настройке результирующие погрешности решения задачи ПИН не возрастают по времени асимптотически (как в способе КИН), а изменяются по гармоническому закону с периодом Шулера и ограниченной амплитудой. К недостаткам способа ПИН следует отнести следующее (табл.1):
- усложнение схемо-технического обеспечения реализации способа ПИН и, как следствие этого, снижение показателей надежности и долговечности интегрированной системы в эксплуатации, а также ухудшение показателей технологичности и экономичности систем,
- усложнение программно-алгоритмического обеспечения реализации способа ПИН и, как следствие этого, ужесточение требований к вычислительной части интегрированной навигационной системы (МК),
- потеря свойства автономности навигационной системы (полная или частичная) для случаев, когда в качестве эталонных навигационных систем используют системы, не обладающие свойством автономности (радиотехнические, спутниковые, астрономические, корреляционно-экстремальные и др.).
Таким образом, путь совершенствования способов решения задачи пространственной инерциальной навигации ПО в околоземном пространстве за счет усложнения схемотехнического и программно-алгоритмического обеспечений построения ИНС приводит к существенному снижению других показателей систем (надежности, долговечности, технологичности, экономичности). Поэтому усилия специалистов в области автономной навигации в дальнейшем (в конце XX- начале XXI столетий) были направлены на поиск способов бесплатформенной инерциальной навигации, которые обеспечивали бы повышение точности решения задачи навигации без снижения других эксплуатационных показателей систем в основном за счет совершенствования приемов обработки информации. Способы ПАНИ-ОФК и ПИН (табл. 1) нашли широкое применение в конце ХХ-начале XXI столетий в практике навигации и управления различными ПО на земле и под землей, на воде и под водой, в атмосфере Земли и околоземном космосе.
Известен способ дифференциально-геометрической инерциальной навигации (ДГИН), в котором алгоритмы обработки инерциальной информации формируют на основе подхода, учитывающего операторы траекторного состояния ПО в виде параметров кривизны и кручения траектории, функционально связанных с векторами положения, скоростей и ускорений [9].
В отличие от способов КИН и ПИН (табл.1) (в которых обеспечивают кинематическое инерциальное счисление пройденного пути по интегральным приемам) в способе ДГИН реализуют принцип счисления пройденных участков траектории ΔSj(j=1,2,…), идентифицируемых по инвариантным параметрам годографов положений с учетом их кривизны (k) и кручения 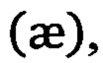 которые в свою очередь однозначно связаны с показаниями ТБН
которые в свою очередь однозначно связаны с показаниями ТБН 

При этом в способе ДГИН удается избежать необходимости применения интегральных приемов (2), (3), (12) и других с использованием выражений (13)- (18). Этого достигают в способе ДГИН за счет замены интегральных приемов обработки инерциальной информации 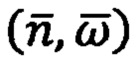 на безынтегральные приемы, в которых вместо независимого аргумента времени t используют информацию об угле между векторами скоростей и ускорений, однозначно идентифицируемую по показаниям инерциальных ДПИ
на безынтегральные приемы, в которых вместо независимого аргумента времени t используют информацию об угле между векторами скоростей и ускорений, однозначно идентифицируемую по показаниям инерциальных ДПИ 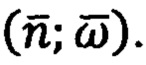
Каждый участок траектории 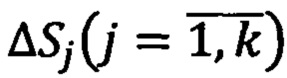 дискретно идентифицируют по параметрам годографов положения, скоростей и ускорений с учетом оценок кривизны (k) и кручения
дискретно идентифицируют по параметрам годографов положения, скоростей и ускорений с учетом оценок кривизны (k) и кручения 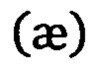 траектории на этом участке. Для этих целей для каждого участка траектории
траектории на этом участке. Для этих целей для каждого участка траектории 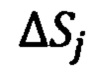 рассматривают его проекцию на горизонтальную плоскость (трассу участка) и проекцию его на прилегающую вертикальную плоскость (профиль участка). Трассу и профиль участка траектории идентифицируют геометрически (с использованием годографов положения) и кинематически (с помощью годографов скоростей и ускорений).
рассматривают его проекцию на горизонтальную плоскость (трассу участка) и проекцию его на прилегающую вертикальную плоскость (профиль участка). Трассу и профиль участка траектории идентифицируют геометрически (с использованием годографов положения) и кинематически (с помощью годографов скоростей и ускорений).
Сущность способа ДГИН заключается в том, что траектория движения любого ПО в околоземном пространстве, задаваемая с помощью годографа векторов положения

может быть полностью и однозначно описана с учетом связи годографа положения 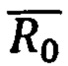 с годографами скорости
с годографами скорости 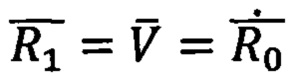 и ускорения
и ускорения 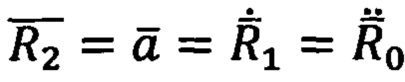 , а также годографов высших производных (если это необходимо):
, а также годографов высших производных (если это необходимо):

и т.д.
В основу способа ДГИН положено свойства соответствия точек траектории, задаваемых с помощью годографа векторов положения нулевого порядка 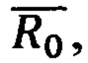 с одной стороны, соответствующим точкам на годографах скоростей
с одной стороны, соответствующим точкам на годографах скоростей 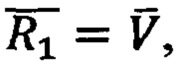 ускорений
ускорений 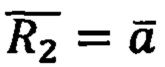 и высших порядков
и высших порядков 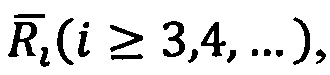 с другой стороны. Эта связь в области времени задается с помощью дифференциальных уравнений [9, стр. 87]:
с другой стороны. Эта связь в области времени задается с помощью дифференциальных уравнений [9, стр. 87]:

и т.д.
где 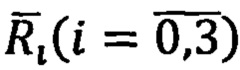 - соответственно, векторы положения
- соответственно, векторы положения 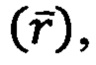 скорости
скорости 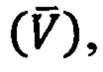 ускорения
ускорения 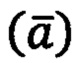 и темпа-скорости нарастания ускорения
и темпа-скорости нарастания ускорения 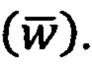 В области пространства (в которой в качестве независимого аргумента используют параметр пройденного по траектории пути - 5) связи (31) выражают с помощью векторно-тензорных уравнений:
В области пространства (в которой в качестве независимого аргумента используют параметр пройденного по траектории пути - 5) связи (31) выражают с помощью векторно-тензорных уравнений:
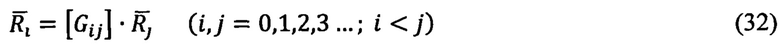
где 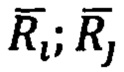 - векторы i -ого и j-ого порядков;
- векторы i -ого и j-ого порядков;
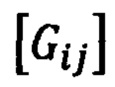 - тензор преобразования векторов из пространства i-ого порядка в пространство j-ого порядка (i < j).
- тензор преобразования векторов из пространства i-ого порядка в пространство j-ого порядка (i < j).
В способе ДГИН для описания геометрии и кинематики движения ПО в околоземном пространстве любой объект принимают за материальную точку, движение которой описывают с помощью уравнений Френе в осях траекторного трехгранника (базиса Френе) 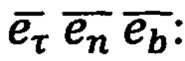

где K(s) - матрица искривления и кручения траектории в данной точке, определяемой аргументом s.
Причем матрица K(s) может быть выражена через кривизну k(s) и кручение 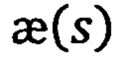 траектории:
траектории:

В реальном околоземном пространстве матрица K(s) выполняет функцию тензора преобразования векторов 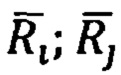 . С учетом тензоров более высоких порядков имеем уравнения векторно-тензорных преобразований [9, стр. 86]:
. С учетом тензоров более высоких порядков имеем уравнения векторно-тензорных преобразований [9, стр. 86]:
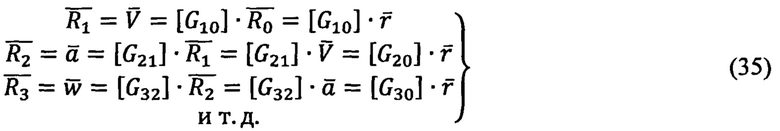
Преобразования (35), заданные в области пространственного аргумента S, эквивалентны кинематическим соотношениям (31), задаваемым в области времени (дифференцирование векторов по времени t).
Уравнения Френе определяют кривую траекторию в пространстве аргумента 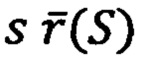 однозначно при задании непрерывных функций кривизны k(s) и кручения
однозначно при задании непрерывных функций кривизны k(s) и кручения 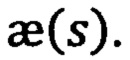
В задачу ДГИН входит идентификация тензоров преобразований 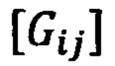 векторов. При этом для определения связи функций кривизны k(s) и кручения
векторов. При этом для определения связи функций кривизны k(s) и кручения  траектории ПО с выходными сигналами инерциальных ДЛИ
траектории ПО с выходными сигналами инерциальных ДЛИ  обычно используют формулы
обычно используют формулы
дифференциальной геометрии:
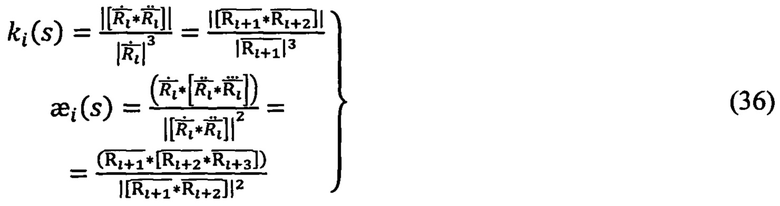
Выражения для правых частей в формулах (36) позволяют связать их с показаниями блоков инерциальных датчиков (ТБН, ТБГ) - 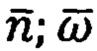 и с их производными по времени.
и с их производными по времени.
Обратный переход от параметра si (в области пространства) к параметризации по времени (во временной области) строят на основе операций дифференцирования:

Отличительными особенностями способа ДГИН являются:
- использование дифференциально-геометрических соотношений между составляющими векторов положения 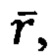 скорости
скорости  и ускорения
и ускорения 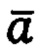 ПО,
ПО,
- независимость процесса и результата решения задачи ДГИН от времени,
- отсутствие накопления погрешностей ДГИН от времени t вследствие использования безынтегральных приемов обработки информации,
- слабая чувствительность в широких пределах эксплуатации приемов ДГИН к внешним возмущениям (автономность способа) и ошибкам измерителей.
Варианты способов ДГИН нашли практическое применение в области космической навигации. В частности, радиально-скоростной радиотехнический способ (вариант способа ДГИН), разработанный советским академиком В.А. Котельниковым, был положен в основу построения первой советской спутниковой навигационной системы (СНС), позволившей решить задачу вывода в 1977 году советского атомного ледокола «Арктика» в географическую точку Северного полюса [9, стр. 34]. Практическое использование способа ДГИН особенно привлекательно и эффективно в тех областях транспортной техники, в которых траектории движения ПО определяют априорно (баллистика МБР и ракет-носителей космических аппаратов (КА), орбитальное движение КА, внутритрубная навигация инспектирующих снарядов, наземная навигация по заданным автомагистралям, железнодорожным путям, подземная навигация ПО в тоннелях (метро), буровых скважинах, движение городского транспорта по заданным маршрутам, локальная персональная навигация внутри зданий, по городским маршрутам, внутри ангаров и территорий портов, маловысотный полет ЛА или придонное движение ПА под водой в режиме следования рельефу местности, перехват целей по заданным сконструированным траекториям перехвата, межорбитальные маневры КА в космосе по переходным траекториям, боевые развороты самолетов, полет ракет-носителей и МБР по программным траекториям вывода КА на орбиту, межпланетные перелеты КА по орбитам сопряжения, глиссадная траектория посадки самолета на взлетно-посадочную полосу или палубу корабля-авианосца и пр.).
К недостаткам способа ДГИН следует отнести следующее:
- сложность приемов обработки информации, в связи с необходимостью учета производных высших порядков (третьего и выше),
- ужесточение требований к метрологическим характеристикам инерциальных измерителей (ньютономеров и гироскопов).
Способ ДГИН в настоявшее время нашел ограниченное применение [9, стр. 34, 37, 46].
Наиболее близким к предлагаемому изобретению является способ автономной дифференциальной геомагнитной навигации (ДГМН), заключающийся в дифференциально-геометрическом позиционировании ПО в околоземном пространстве [10].
Способ не относится к группе способов инерциальной навигации (табл. 1), однако в научно-методическом отношении близок к альтернативному способу и принят в качестве способа-прототипа. Способ ДГМН относится к группе способов автономной безынтегральной навигации по геофизическим полям (ГФП) [11, 12].
Отличительными особенностями способа ДГМН являются следующие достоинства (табл.1):
- автономность,
- безгироскопный способ,
- бесплатформенный,
- безынтегральный
- некинематический (не способ кинематического счисления пути, а способ геометрического позиционирования),
- технологичность и экономичность системы ДГМН.
Сущность способа ДГМН заключается в геометрическом позиционировании ПО относительно априорно заданных опорных реперных точек (ОРТ) геомагнитной сетки (ГМС), выполняемом косвенным путем на основе обработки геомагнитной информации, характеризующей параметры магнитного поля Земли (МПЗ) в ОРТ ГМС и в точке текущего местоположения ПО в околоземном пространстве.
В соответствии с основными положениями способа ДГМН все или его часть околоземного пространства покрыто сетью контрольных ОРТ (СОРТ)  в которых априорно заданы следующие параметры:
в которых априорно заданы следующие параметры:
- географические координаты точек  характеризующие радиус-вектор
характеризующие радиус-вектор 
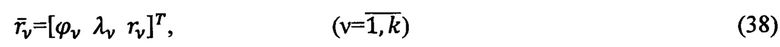
- параметры МПЗ, отнесенные к географическому базису 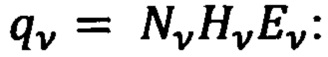
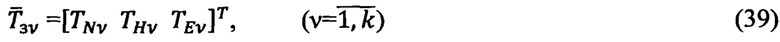
где 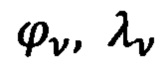 - географическая широта и долгота v-ой контрольной ОРТ
- географическая широта и долгота v-ой контрольной ОРТ 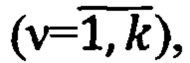
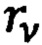 модуль радиуса-вектора
модуль радиуса-вектора 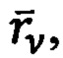
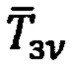 - вектор напряженности МПЗ в v-ой контрольной ОРТ,
- вектор напряженности МПЗ в v-ой контрольной ОРТ,
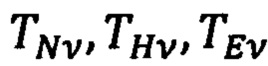 - северная, вертикальная и восточная составляющие вектора
- северная, вертикальная и восточная составляющие вектора 
Шаг дискретизации ГМС 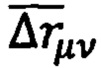 выбирают исходя из ограничений на разностный вектор
выбирают исходя из ограничений на разностный вектор

сформированных по условиям масштабов и допустимых погрешностей решения задачи геомагнитной навигации.
Описание МПЗ в точке А текущего местоположения ПО и в контрольных ОРТ 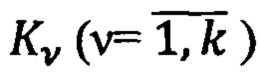 строят на основе теории геомагнитного потенциала U в соответствии с международной моделью WMM - IGRF [13]:
строят на основе теории геомагнитного потенциала U в соответствии с международной моделью WMM - IGRF [13]:
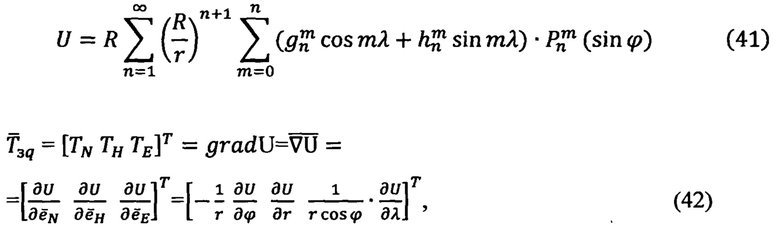
где 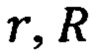 - радиусы текущей точки и ее проекции на поверхности Земли,
- радиусы текущей точки и ее проекции на поверхности Земли,
 - степень и порядок разложения геомагнитного потенциала в гармонические ряды сферических функций,
- степень и порядок разложения геомагнитного потенциала в гармонические ряды сферических функций,
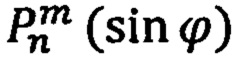 - полиномы Лежандра степени n порядка m.
- полиномы Лежандра степени n порядка m.
Численные значения коэффициентов 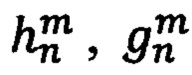 уточняют периодически не реже одного раза в 5 лет. Последняя версия международного стандарта WMM-2020 [13].
уточняют периодически не реже одного раза в 5 лет. Последняя версия международного стандарта WMM-2020 [13].
Магнитометрическую информацию о компонентах 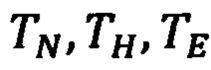 вектора
вектора 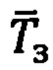 в точке текущего мостоположения ПО формируют с помощью трехосного блока магнитометров (ТЕМ):
в точке текущего мостоположения ПО формируют с помощью трехосного блока магнитометров (ТЕМ):

Путем сравнения векторов 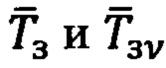 формируют разностный вектор:
формируют разностный вектор:
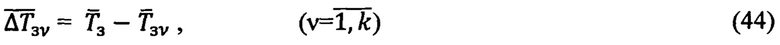
Причем
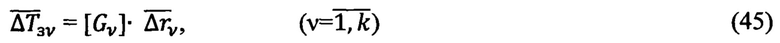
где  - радиус-вектор корреляции текущей точки А относительно
- радиус-вектор корреляции текущей точки А относительно
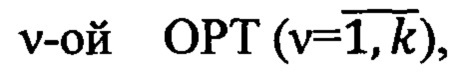
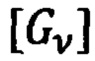 - тензор МПЗ в v-ой ОРТ.
- тензор МПЗ в v-ой ОРТ.
Тензор МПЗ в v-ой ОРТ вычисляют как градиент вектора 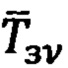 [12]:
[12]:
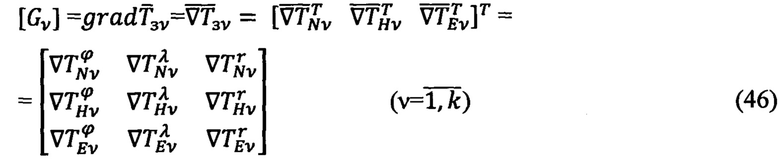
В каждый момент времени точка А текущего местоположения ПО образует с каждой v-ой контрольной ОРТ 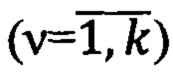 и центром 0 Земли навигационные треугольники
и центром 0 Земли навигационные треугольники 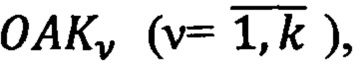 для которых можно написать основное уравнение геометрической (позиционной) навигации [6, 7,11,12]:
для которых можно написать основное уравнение геометрической (позиционной) навигации [6, 7,11,12]:
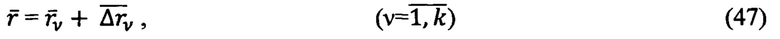
Или
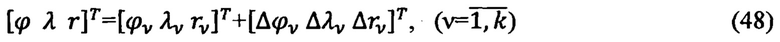
Умножая уравнение (45) слева на обратную матрицу  , получают решение для радиуса-вектора корреляции
, получают решение для радиуса-вектора корреляции 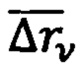 , а затем формируют прием обработки информации ДГМН:
, а затем формируют прием обработки информации ДГМН:
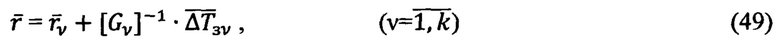
Конкретизируя выражение для обратной матрицы 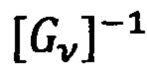 , получают решения навигационных треугольников
, получают решения навигационных треугольников 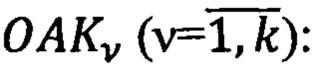
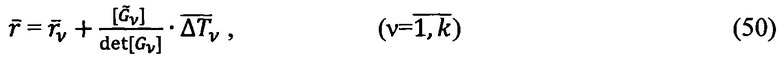
где 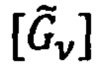 - союзная (присоединенная) матрица,
- союзная (присоединенная) матрица,
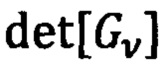 - детерминант матрицы
- детерминант матрицы 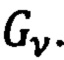
Для исключения явления вырождения решения (50) для v-ой контрольной ОРТ необходимо выполнение условия:
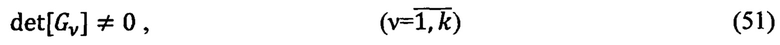
Осреднением радиусов-векторов 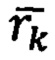 , определенных для всех к ОРТ с учетом выполнения условия (51), получают оценку радиуса-вектора
, определенных для всех к ОРТ с учетом выполнения условия (51), получают оценку радиуса-вектора 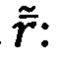

Прием обработки информации для способа ДГМН включает в свой состав выражения (41) - (52), реализуемые в бортовом вычислителе.
Отличия способа ДГМН от способов инерциальной навигации - КИН, ПИН (табл. 1):
- вычисление радиуса-вектора корреляции 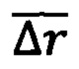 производят в области пространства, а не в области времени t,
производят в области пространства, а не в области времени t,
- используют дифференциально-конечные приемы геометрического позиционирования ПО, а не интегральные приемы кинематического инерциального счисления пройденного пути,
- в способе ДГМН отсутствует процесс накопления во времени погрешностей, т.к. прием обработки информации ДГМН безынтегральный.
В способе ДГМН, как и в способе ДГИН, используют безынтегральные приемы обработки информации. Однако в способе ДГМН операторы преобразования магнитометрической информации задают как параметры внешней среды (компоненты и градиенты МПЗ), а в способе ДГИН операторы преобразования инерциальной информации 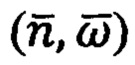 связаны с оценкой параметров пройденной траектории движения ПО (кривизной k(s) и кручением
связаны с оценкой параметров пройденной траектории движения ПО (кривизной k(s) и кручением 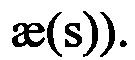 Следовательно, в способе ДГМН обеспечивают условия инвариантности (независимости) операторов преобразования информации от параметров самой траектории (использование траекторно-независимых операторов).
Следовательно, в способе ДГМН обеспечивают условия инвариантности (независимости) операторов преобразования информации от параметров самой траектории (использование траекторно-независимых операторов).
В способе ДГИН реализуют принцип обработки информации в режиме off-line (обеспечивают условия для формирования траекторно-зависимых операторов преобразования информации - кривизны и кручения пройденной в прошлом траектории), а в способе ДГМН реализуют принцип обработки информации в режиме on-line, т.к. приемы ДГМН предполагают использование информации в реальном масштабе времени о траекторно-независимых операторах обработки информации - о градиентах МПЗ). Градиенты МПЗ в способе ДГМН являются аналогами градиентов траектории (кручения и кривизны) в способе ДГИН. В способе ДГМН не требуется определять производные высших порядков (третьего и выше).
Если в способе ДГИН операторы обработки информации (матрицы кривизны и кручения траектории) характеризуют степень искривленности и скрученности в пространстве траектории, а также степень отклонения траектории от идеальной прямолинейной траектории 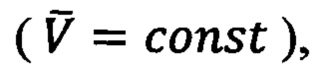 то в способе ДГМН операторы обработки информации в виде тензоров градиентов МПЗ характеризуют степень искривленности в пространстве линий магнитной индукции геомагнитного поля и степень отклонения МПЗ от однородного ГФП
то в способе ДГМН операторы обработки информации в виде тензоров градиентов МПЗ характеризуют степень искривленности в пространстве линий магнитной индукции геомагнитного поля и степень отклонения МПЗ от однородного ГФП 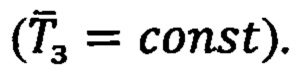
В сравнении способа ДГМН со способом ДГИН можно отметить следующие преимущества:
- в способе ДГМН имеются условия для формирования функционально избыточной информации вследствие возможности организации синхронных многоточечных оценок разностной магнитометрической информации относительно нескольких контрольных ОРТ,
- в способе ДГМН имеется возможность решения задачи прогнозирования формирования траектории движения ПО, а в способе ДГИН такие возможности ограничены.
Вместе с тем способ ДГМН обладает существенным недостатком, связанным с проявлением погрешностей геомагнитного позиционирования ПО в околоземном пространстве, обусловленных влиянием аномалий и вариаций МПЗ на точность решения задачи ДГМН.
Задача настоящего изобретения заключается в разработке такого способа автономной навигации с использованием инерциальной информации 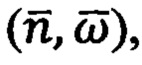 который был бы свободным от недостатков способов-аналогов и способа-прототипа, а именно:
который был бы свободным от недостатков способов-аналогов и способа-прототипа, а именно:
- был бы автономным и не требовал привлечения дополнительной (например, спутниковой, магнитометрической или другой информации),
- обеспечивал условия для получения функционально-избыточной информации как на стадии измерений, так и на стадии обработки полученной информации,
- гарантировал условия, при которых реализация способа не была сопряжена с ухудшением важных технологических, экономических и эксплуатационных показателей (технологичности, экономичности, надежности, отказоустойчивости, простоты реализации).
Достижение поставленной задачи выполняют за счет того, что:
- обеспечивают формирование ППИ с учетом условия получения функционально избыточной информации от многоосных блоков гироскопов и ньютономеров с неортогональными осями чувствительностей,
- выполняют обработку полученной многомерной информации в условиях функциональной избыточности информации по алгебраическим конечно-разностным приемам,
- повышают степень достоверности полученной выходной информации за счет использования при финишной обработке информации приемов автономного контроля, нормировки, обеспечения условий самотестирования, функциональной избыточности информации и отказоустойчивости системы в эксплуатации.
Предлагаемое изобретение поясняется чертежами (Фиг. 1-Фиг. 6).
На фигуре 1 представлена схема формирования математической модели пространственной автономной навигации инерциальной (ПАНИ).
На фигуре 2 представлена функциональная схема взаимодействия информационно-измерительной системы (ИИС) наблюдающего устройства (НУ) с динамической системой (ДС).
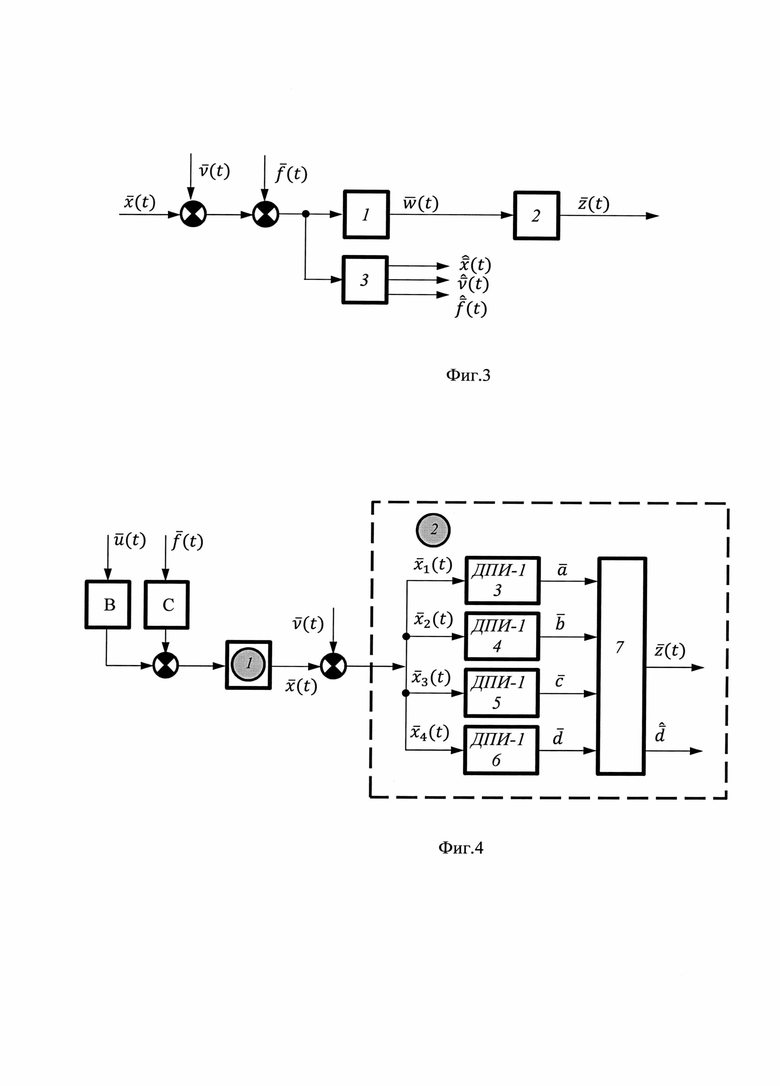
На фигуре 3 указана схема взаимодействия формирующего фильтра (ФФ) с ДС и ИИС в способе комплексирования и фильтрации.
На фигуре 4 представлена схема построения комбинированного измерительно-вычислительного комплекса (ИВК), работающего по способу комбинированной обработки многомерной информации в комплексе (КОМИК).
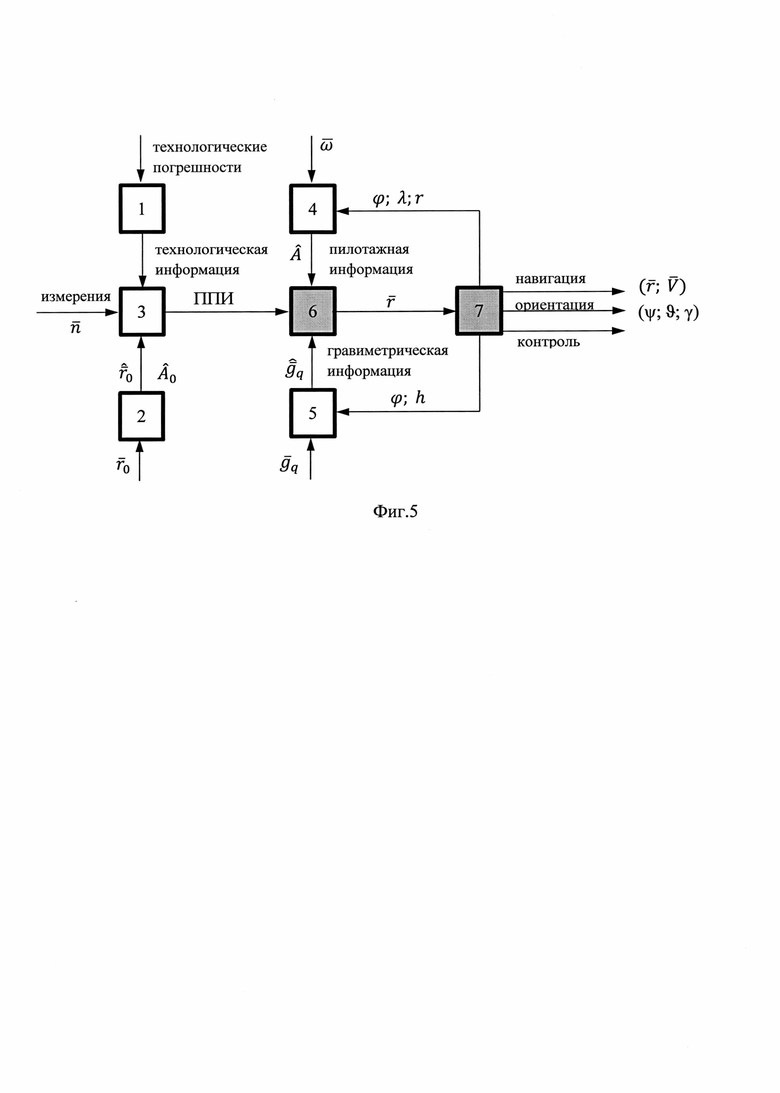
На фигуре 5 представлена функциональная схема выполнения операций измерений, калибровки, начальной выставки и обработки многомерной информации в способе дифференциальной инерциальной навигации (ДИН).
Схема формирования рядов импульсов представлена на фигуре 6.
На фигуре 2 приняты следующие обозначения:
1 - динамическая система (ДС), подлежащая наблюдению (измерениям),
2 - информационно-измерительная система (ИИС), выполняющая
функции наблюдающего устройства (НУ) и осуществляющая наблюдение за ДС (измерения),
3 - блок оценки и коррекции (БОК),
4 - отрицательная обратная связь (ООС), выполняющая функции коррекции.
На фигуре 3 введены следующие обозначения:
1- ДС,
2- ИИС,
3 - формирующий фильтр (ФФ). Обозначения, принятые на фигуре 4:
1- ДС,
2- ИВК,
3, 4, 5, 6 - блоки датчиков первичной информации (ДЛИ), 7 - микроконтроллер.
На фигуре 5 приняты следующие обозначения функциональных блоков, соответствующих операциям измерений, подготовки и обработки многомерной информации:
1 - блок технологических калибровок (инструментальных и объектовых),
2 - блок начальной автономной выставки (НАВ),
3 - блок измерений, формирования первичной приборной информации (ППИ) и ее предварительной обработки,
4 - блок автономной ориентации (например, АПО-[14]),
5 - блок гравиметрии (БГМ),
6 - блок дифференциальной инерциальной навигации (ДИН),
7 - блок выполнения операций автономного контроля и нормировки (АКН).
Сущность предлагаемого способа бесплатформенной автономной навигации заключается в том, что
- с помощью многоосных неортогональных блоков векторных датчиков (ньютономеров, гироскопов), предварительно откалиброванных, формируют многомерную первичную приборную информацию (ППИ) в условиях функциональной избыточности информации о векторах кажущегося ускорения 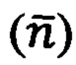 и абсолютной угловой скорости вращения объекта
и абсолютной угловой скорости вращения объекта 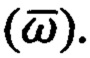
- затем расширяют многомерную информацию за счет решения задач начальной автономной выставки (НАВ), автономной ориентации, гравиметрии
- и наконец, на основе расширенной многомерной инерциальной информации определяют компоненты вектора относительной скорости 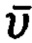 объекта и его полярные координаты
объекта и его полярные координаты 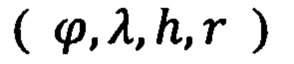 в географическом базисе путем обработки многомерной информации по алгебраическим конечно - разностным приемам в условиях функциональной избыточности информации с учетом начальных условий.
в географическом базисе путем обработки многомерной информации по алгебраическим конечно - разностным приемам в условиях функциональной избыточности информации с учетом начальных условий.
Отличительная особенность предлагаемого способа бесплатформенной автономной навигации заключается в приеме обработки многомерной информации.
Обработку информации в способах КИН, ПИН (табл.1) строят исходя из принципа кинематического инерциального счисления пройденного пути, а приемы обработки той же информации в способе ДИН строят исходя из принципа, конечно - разностного позиционирования точки текущего местоположения объекта в подвижном отсчетном базисе.
Таким образом, принципиальное отличие предлагаемого способа ДИН от существующих способов инерциалной навигации заключается в разных приемах обработки инерциальной информации).
Способ ДИН заключается в последовательном выполнении следующих операций (Фиг. 5).
1. Операции технологических калибровок имеют своей целью идентификацию индивидуальных параметров измерителей (ньютономеров, гироскопов), определяющих их метрологические характеристики, а также технологические погрешности сборки в блоках и монтажа (установки) на объекте.
Вопросы технологического обеспечения операций технологических калибровок достаточно обстоятельно рассмотрены в научно-технической и патентной литературе [6].
2. Операции автономной начальной выставки (АВН) выполняют с целью определения параметров начальных условий:

Начальные значения полярных координат 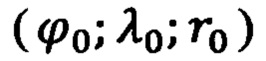 точки старта ПО обычно определяют с помощью спутниковой навигационной системы (СНС).
точки старта ПО обычно определяют с помощью спутниковой навигационной системы (СНС).
С учетом неподвижности ПО относительно Земли в предстартовых условиях определяют показания трехосных блоков (ньютономеров, гироскопов):
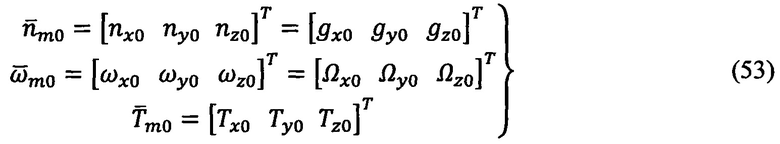
Зная начальные значения вектора полярных координат 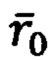 на основе известных моделей ГФП (WGS-84) можно определить векторы ГФП в географическом стартовом отсчетном базисе
на основе известных моделей ГФП (WGS-84) можно определить векторы ГФП в географическом стартовом отсчетном базисе 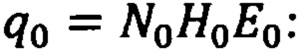

С учетом (53) и (54) можно составить матричное уравнение:
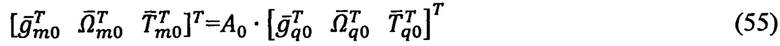
Умножением матричного уравнения (55) слева на обратную матрицу идентификации начальных условий

получают уравнение НАВ в матричной форме:
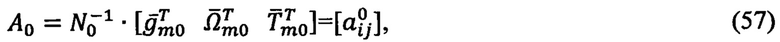
где 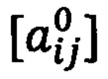 - начальные значения направляющих косинусов матрицы ориентации А0.
- начальные значения направляющих косинусов матрицы ориентации А0.
ПО в предстартовых условиях.
Начальные значения эйлеровых углов 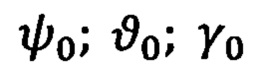 вычисляют по известным направляющим косинусам
вычисляют по известным направляющим косинусам 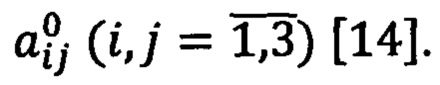
3. Операции измерений и формирования ППИ выполняют на основе показаний трехосных блоков векторных датчиков (ньютономеров, гироскопов) в каждой точке А текущего местоположения ПО в околоземном пространстве:

При формировании ППИ в скорректированной и приведенной форме (58) учитывают результаты выполнения подготовительных операций в блоках 1 и 2 (Фиг. 5).
4. Операции автономной ориентации выполняют как операции сервисной вспомогательной задачи. Уравнение автономной ориентации ПО аналогичен уравнению (57) [14]:

При этом матрицу идентификации N (3 * 3) формируют на основе информации о векторах ГФП в текущей точке А

Причем компоненты векторов ГФП 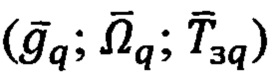 определяют с учетом информации о движении и вращении объекта в околоземном пространстве.
определяют с учетом информации о движении и вращении объекта в околоземном пространстве.
Векторы 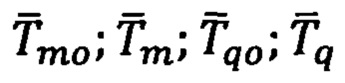 находят на основе векторных произведений соответствующих векторов.
находят на основе векторных произведений соответствующих векторов.
По найденным направляющим косинусам 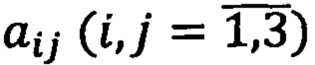 матрицы ориентации находят оценки эйлеровых углов
матрицы ориентации находят оценки эйлеровых углов 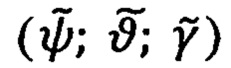 в условиях функциональной избыточности информации [14, 15].
в условиях функциональной избыточности информации [14, 15].
5. Операции задачи гравиметрии, как сервисной задачи, выполняют с целью определения компонент вектора удельной силы тяжести  в текущей точке А по модели поля тяжести Земли (ПТЗ). Для стандартной модели ПТЗ можно написать основное уравнение гравиметрии [5]:
в текущей точке А по модели поля тяжести Земли (ПТЗ). Для стандартной модели ПТЗ можно написать основное уравнение гравиметрии [5]:

Или в численной форме:
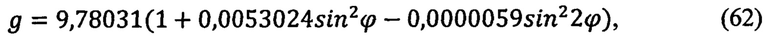
где 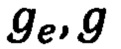 - удельные силы тяжести на экваторе и в текущей точке на поверхности Земли.
- удельные силы тяжести на экваторе и в текущей точке на поверхности Земли.
Вектор 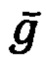 в произвольной точке околоземного пространства имеет северную (gN) и вертикальную (gH) составляющие:
в произвольной точке околоземного пространства имеет северную (gN) и вертикальную (gH) составляющие:

Причем эти составляющие 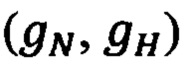 находят по формулам (18).
находят по формулам (18).
6. Операции решения задачи ДИН составляют ядро функциональной схемы решения задачи ДИН (Фиг. 5) и содержат отличительные признаки предлагаемого способа навигации. Фиксируют показания блоков ньютономеров в соседние дискретные моменты времени (v-1 и v):
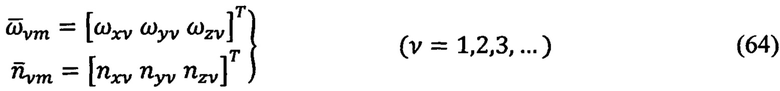
Причем в любой момент времени
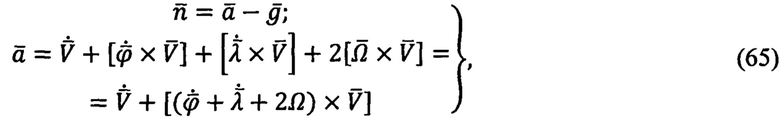
где 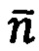 - кажущееся ускорение,
- кажущееся ускорение,
 - относительное ускорение,
- относительное ускорение,
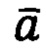 - абсолютное ускорение.
- абсолютное ускорение.
Приведенные к географическому базису q=NHE разностные показания ТБН равны:
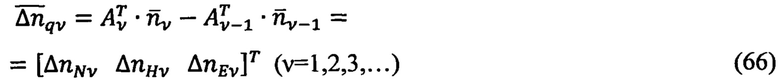
Уравнения (65) после подстановки в них выражения (66) приводят к векторно-матричному уравнению в конечных разностях[16]:

Уравнение автономного определения скорости ПО
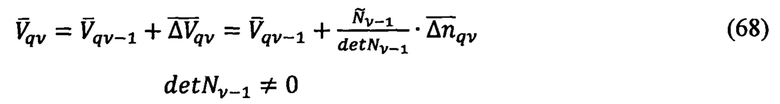
На основе уравнения (68) получают уравнение определения координат 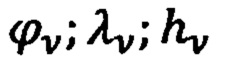 ПО с учетом выражений (18) на каждом ом цикле обновления информации:
ПО с учетом выражений (18) на каждом ом цикле обновления информации:

Совокупность выражений (68) - (70) образует дифференциальный прием решения задачи ДИН.
7. Операции автономного контроля и нормировки (АКН) выполняют в блоке 7 (Фиг. 5) с целью проверки правильности и корректности результатов. Приемы АКН сводятся к оценкам найденных величин и к сравнению их с эталонными значениями:

В сравнении со способами автономной навигации (КИН-ОФК, ДГИН, ДГМН) предлагаемый способ ДИН выгодно отличается по показателям простоты реализации, технологичности, надежности, долговечности, отказоустойчивости навигационной системы, построенной по способу ДИН.
В соответствии с ауравнениями ДИН (выражения (52) - (71)) в предлагаемом способе решения задачи инерциальной навигации обработка информации предполагает использование многомерной многофункциональной информации (Фиг. 5):
- технологической,
- информации о начальной выставке ПО 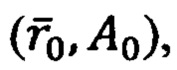
- пилотажной информации (информации об ориентации 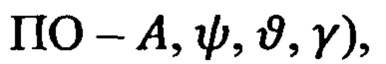
- первичной приборной информации 
- гравиметрической информации 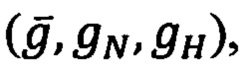
- навигационной информации 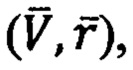
- контрольно-нормирующей информации.
В предлагаемом способе ДИН с целью повышения эксплуатационных показателей точности, надежности, самопроверяемости, отказоустойчивости в соответствии с принципом функциональной избыточности информации и мультимодульному принципу для формирования ППИ вместо трехосных блоков ньютономеров (ТБН) и гироскопов (ТБГ) используют многоосные блоки (МБН, МБГ), построенные по неортогональным схемам измерений [15].
Практическая реализация многоосных блоков векторных датчиков (ньютономеров, гироскопов) может быть выполнена на отечественной или импортной элементной базе. К примеру, в качестве векторных датчиков в системе ДИН могут быть использованы:
- маятниковые кварцевые ньютономеры AT-1184 производства НПП «Темп-Авиа» (г.Арзамас),
- волоконно-оптические гироскопы типа ВОГ-951 производства НПО «Физоптика» (г.Москва).
Численные оценки расчетным путем показывают, что для решения задачи автономной навигации ПО способом ДИН с допустимыми погрешностями позиционирования, не превышающими нескольких сот метров (до 1 км) достаточно использовать в составе навигационной системы блоки векторных датчиков, имеющих инструментальные погрешности первичных измерений, не превышающие пороговых (допустимых) величин:
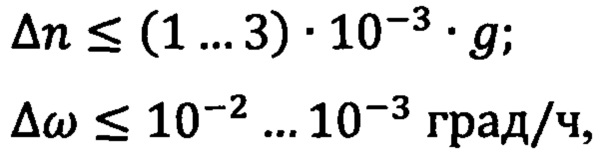
что соответствует уровню достижимых погрешностей для существующих (а тем более, для перспективных) векторных датчиков.
Формирование ППИ и ее преобразование (Фиг. 5) производят дискретно с тремя частотами обработки и обновления информации (Фиг. 6):
- тактовой частотой 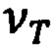 с длительностью такта
с длительностью такта 
- шаговой частотой 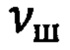 обновления пилотажной информации с длительностью одного шага
обновления пилотажной информации с длительностью одного шага 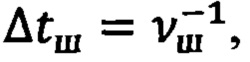
- циклической частотой v4 обновления навигационной информации с длительностью одного цикла 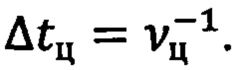
Причем для эффективного и рационального использования микроконтроллера в составе системы ДИН выполняют условия синхронизации и согласования выполняемых операций обработки 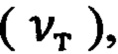 обновления пилотажной информации
обновления пилотажной информации 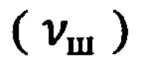 и обновления навигационной информации
и обновления навигационной информации 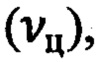 реализуемые в виде неравенств (Фиг. 6):
реализуемые в виде неравенств (Фиг. 6):

Области практического применения предлагаемого способа ДИН ограничены лишь масштабами околоземного пространства:
- на земле и под землей для наземных ПО,
- на воде и под водой для плавающих и подводных ПО,
- в воздухе для летательных и баллистических аппаратов,
- в околоземном космосе для космических аппаратов.
Приведем перечень отличительных положительных особенностей предлагаемого способа ДИН ПО:
1. Способ ДИН полностью автономен по всем каналам ориентации, навигации, контроля и нормировки информации.
2. Способ ДИН обеспечивает 100%-ю покрываемость территории земной поверхности и акватории морей и океанов, 100%-ю проникающую способность независимо от особенностей рельефа местности (овраги, горы, лесистость, тоннели; на земле и под землей; на воде и под водой; в атмосфере и околоземном космосе).
3. Способ ДИН благодаря принципу функциональной избыточности информации и мультимодульному принципу обеспечивает в эксплуатации навигационной системе условия всепогодности, всережимности использования, условия устойчивости, невыбиваемости, невырождаемости уравнений обработки информации с системой встроенного контроля (СВК), самодиагностики и самотестирования, с режимом отказоустойчивости в резервно-аварийных режимах (РАР).
4. Приемы ДИН для обработки геофизической информации обладают свойством универсальности, обеспечивающим возможность использования системы в наземной и ракетно-космической технике, в авиации и морском флоте.
5. Способ ДИН гарантирует нормальную работу каналов автономной ориентации и автономной навигации одновременно по параллельным каналам идентификации в разночастотных режимах (в разных темпах), учитывающих частотные динамические свойства объектов.
6. Способ ДИН основан на использовании бесплатформенных, бесспутниковых, безынтегральных, бездевиационных цифровых технологий получения и программно-алгоритмической обработки многомерной информации, реализуемых с помощью малогабаритных и миниатюрных измерительно-вычислительных систем.
7. Способ ДИН предполагает реализацию многорежимной и многофункциональной работы системы, достигаемой при их неизменной аппаратной части за счет сменного программно-алгоритмического обеспечения и ориентированной на полную совместимость систем ДИН с другими системами ориентации и навигации путем реализации режимов комплексирования, комбинирования, коррекции, автономной работы и РАР.
Анализ отечественной и зарубежной научно-технической литературы, и патентных источников за последние десятилетия XX века показывает, что альтернативы предложенному способу ДИН в настоящее время не существует.
Список источников
1. Ориентация и навигация подвижных объектов. Современные информационные технологии / Под общ. ред. Б. С. Алешина, К. К. Веремеенко, А. И. Черноморского. - М.: Физматлит, 2006. - 424 с.
2. Матвеев В. В., Распопов В. Я. Основы построения бесплатформенных инерциальных навигационных систем. - СПб.: ГНЦ РФ ОАО «Концерн ЦНИИ «Электроприбор»», 2009. -280 с.
3. Ткачев Л.И. Системы инерциальной ориентировки / Учебное пособие, ч. I. Основные положения теории/Под ред. Г. Н. Сенилова- М..МЭИ, 1973.-215 с.
4. Андреев В. Д. Теория инерциальной навигации, ч. I. Автономные системы. - М.: Наука, 1966.-529 с. ч. И. Корректируемые системы. - М.: НаукаД967. -648 с.
5. Руководство по Всемирной геодезической системе. - 1984 (WGS-84). Международная организация гражданской авиации IKAO, изд. 2-ое, 2002, DOC 9674.
6. Игнатьев А. А., Проскуряков Г. М. Гетеромагнитометрия: алгоритмы, методики, калибровки блоков магнитометров / А. А. Игнатьев, Г. М. Проскуряков. - Саратов: Изд-во Сарат.ун-та, 2014.-152 с.
7. Степанов О. А. Основы теории оценивания с приложениями к задачам обработки навигационной информации, ч. 1. Введение в теорию оценивания. - СПб.: ГНЦ РФ ЦНИИ «Электроприбор», 2009. - 496 с.
8. Пат.RU №2757828 С1 МПК: G05D 1/00; G05B 23/00; G06F 11/00. Способ восстановления векторной информации в информационно-измерительных системах / Авторы: Проскуряков Г. М., Голованов П.Н., Пыльский В. А.; патентообладатель: Саратовский госуд. техн. ун-т им. Гагарина Ю. А., опубл. 21.10.21, Бюл. №30.
9. Громов Г. Н. Дифференциально-геометрический метод навигации. - М.: Радио и связь, 1986.- 384 с.
10. Пат.RU №2523753 МПК CI G01C 21/00. Способ персональной автономной навигации / Авторы: Проскуряков Г. М., Буров А. С; патентообладатель: Сарат. госуд. техн. ун-т им. Гагарина Ю. А., опубл. 20.07.2014, Бюл. №20.
11. Белоглазов И. И., Джанджгава Г. И., Чигин Г. П. Основы навигации по геофизическим полям. - М.: Наука, 1985. - 328 с.
12. Помыкаев И. И., Селезнев В. П., Дмитроченко Л. А. Навигационные приборы и системы: Учеб. Пособие для вузов / Под ред. И. И. Помыкаева. - М.: Машиностроение, 1983. - 456 с.
13. International Geomagnetic Reference Field IGRF WMM-2020, URL: http://www.ngdc.noaa.gov.com (дата обращения: 25.12.21)
14. Пат. RU №2653967 МПК: C1 G01 21/00. Способ автономной ориентации подвижных объектов / Авторы: Проскуряков Г. М., Голованов П.Н.; Попов А. Н., Тетерин Д. П.; патентообладатель: ФГБОУ ВО Сарат. госуд. техн. ун-т им. Гагарина Ю. А. от 20.06.2017, опубл. 15.05.2018, Бюл. №14.
15. Епифанов А. Д. Надежность систем управления. Справочная литература инженера-конструктора. - М.: Машиностроение. 1975. - 180 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| АВТОНОМНЫЙ КОМПЛЕКС ДЛЯ КОРРЕКЦИИ ИНЕРЦИАЛЬНЫХ СИСТЕМ ПЛАТФОРМЕННОЙ ОРИЕНТАЦИИ И НАВИГАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2022 |
|
RU2826826C2 |
| Способ автономной ориентации объектов в околоземном пространстве | 2022 |
|
RU2787971C1 |
| СПОСОБ АВТОНОМНОЙ ИНЕРЦИАЛЬНОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2022 |
|
RU2800846C1 |
| СПОСОБ БЕСПЛАТФОРМЕННОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2022 |
|
RU2784859C1 |
| СПОСОБ ПЕРСОНАЛЬНОЙ АВТОНОМНОЙ НАВИГАЦИИ | 2013 |
|
RU2523753C1 |
| Способ восстановления векторной информации в информационно-измерительных системах | 2020 |
|
RU2757828C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ МОДЕЛИ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ АКСЕЛЕРОМЕТРОВ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ ПО ИЗМЕРЕНИЯМ СПУТНИКОВОЙ НАВИГАЦИИ | 2012 |
|
RU2504734C1 |
| СПОСОБ АВТОНОМНОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2017 |
|
RU2653967C1 |
| КОМПЛЕКСНАЯ НАВИГАЦИОННАЯ СИСТЕМА ЛЕТАТЕЛЬНОГО АППАРАТА | 2015 |
|
RU2590935C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ МОДЕЛИ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ АКСЕЛЕРОМЕТРОВ ВЕДОМОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ ПО ИЗМЕРЕНИЯМ ЭТАЛОННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2012 |
|
RU2505785C1 |

Изобретение относится к области бортового приборостроения и может быть использовано для решения пилотажно-навигационных задач при автономном управлении подвижными объектами (ПО). Сущность предлагаемого способа бесплатформенной инерциальной навигации заключается в выполнении следующих этапов: технологическая калибровка ньютономеров и гироскопов; автономная начальная выставка с целью определения параметров начальных условий; формирование первичной приборной информации на основе измерений трехосных блоков ньютономеров и гироскопов в каждой точке текущего местоположения ПО; операция автономной ориентации, при которой компоненты векторов геофизического поля определяют с учетом информации о движении и вращении объекта в околоземном пространстве; определение компонент вектора удельной силы тяжести в текущей точке нахождения ПО; фиксация показаний блока ньютономеров в дискретные моменты времени; определение координат на каждом цикле обновления приборной информации; автономный контроль и нормировка путём сравнения найденных величин параметров с эталонными. Техническим результатом заявленного способа является реализация многофункциональной работы навигационной системы дифференциальной инерциальной навигации, полностью совместимой с другими системами навигации. 6 ил., 1 табл.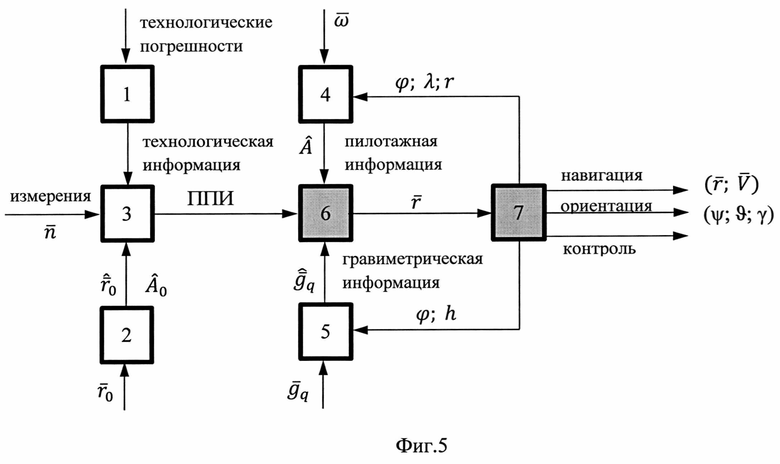
Способ бесплатформенной инерциальной навигации в околоземном пространстве, основанный на измерениях векторов кажущегося ускорения ( ) и абсолютной угловой скорости вращения
) и абсолютной угловой скорости вращения 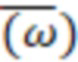 объекта в инерциальном пространстве с помощью многоосных неортогональных блоков предварительно откалиброванных датчиков - ньютономеров, гироскопов - и формировании по результатам этих измерений (
объекта в инерциальном пространстве с помощью многоосных неортогональных блоков предварительно откалиброванных датчиков - ньютономеров, гироскопов - и формировании по результатам этих измерений ( ,
, 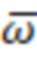 ), а также данных о начальных условиях, найденных при предварительно выполненной в предстартовых условиях автономной начальной выставке, и данных о параметрах ориентации объекта (А), найденных по сигналам (
), а также данных о начальных условиях, найденных при предварительно выполненной в предстартовых условиях автономной начальной выставке, и данных о параметрах ориентации объекта (А), найденных по сигналам (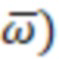 блока гироскопов, многомерной первичной приборной информации в виде приведенных к осям связанного с объектом отсчетного базиса сигналов датчиков (
блока гироскопов, многомерной первичной приборной информации в виде приведенных к осям связанного с объектом отсчетного базиса сигналов датчиков ( ,
, 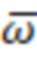 ) с последующей дискретной обработкой этих сигналов и данных о начальных условиях при функциональной избыточности информации, отличающийся тем, что формирование первичной приборной информации и её обработку выполняют следующим образом: определяют на двух соседних циклах (ν и (ν-1)) обновления информации конечные разности приведенных показаний блока ньютономеров, затем по найденным векторам разностей показаний блока ньютономеров определяют конечные разности векторов скорости объекта относительно Земли и разности векторов координат точек местоположения объекта для этих циклов обновления информации, на основе найденных конечных разностей векторов с учетом ранее определенных при начальной автономной выставке начальных условий к моменту окончания каждого ν-ого цикла обновления информации (
) с последующей дискретной обработкой этих сигналов и данных о начальных условиях при функциональной избыточности информации, отличающийся тем, что формирование первичной приборной информации и её обработку выполняют следующим образом: определяют на двух соседних циклах (ν и (ν-1)) обновления информации конечные разности приведенных показаний блока ньютономеров, затем по найденным векторам разностей показаний блока ньютономеров определяют конечные разности векторов скорости объекта относительно Земли и разности векторов координат точек местоположения объекта для этих циклов обновления информации, на основе найденных конечных разностей векторов с учетом ранее определенных при начальной автономной выставке начальных условий к моменту окончания каждого ν-ого цикла обновления информации (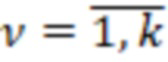 ) определяют конечные значения навигационных векторов объекта.
) определяют конечные значения навигационных векторов объекта.
| СПОСОБ АВТОНОМНОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2017 |
|
RU2653967C1 |
| Способ инерциальной навигации беспилотного летательного аппарата и устройство для его осуществления | 2020 |
|
RU2744700C1 |
| СПОСОБ ПЕРСОНАЛЬНОЙ АВТОНОМНОЙ НАВИГАЦИИ | 2013 |
|
RU2523753C1 |
| US 0006647352 B1, 11.11.2003 | |||
| CN 0109931955 A, 25.06.2019. | |||
Авторы
Даты
2023-11-03—Публикация
2022-06-14—Подача