Изобретение относится к радиолокации и может быть использовано в радиолокационной станции (РЛС) сопровождения низколетящих целей под малыми углами места при наличии мешающих отражений от подстилающей поверхности.
В практической работе современных РЛС одной из важнейших задач является обнаружение и сопровождение низко летящих целей (НЛЦ). При сопровождении НЛЦ важно как можно раньше правильно определить ее угломестную координату (оценить высоту ее полета), чему мешают значительные угломестные ошибки из-за многопутного распространения (явления многолучевости), иначе говоря, из-за сигнала так называемого «антипода» - сигнала, отраженного от подстилающей поверхности.
В результате появления сигнала «антипода» в угломестном разностном канале появляется ложный сигнал ошибки, из-за чего следящая система (СС) по углу места сдвигает луч антенны РЛС до тех пор, пока этот ложный сигнал не будет скомпенсирован. При сопровождении на малых углах места ошибка из-за многопутного распространения очень велика, так как сигнал «антипода» попадает в главный лепесток диаграммы направленности (ДН) антенны РЛС. При этом реальная НЛЦ и сигнал «антипода» образуют двухточечную цель с изменяющейся разностью фаз и амплитудами сигналов, которые сравнимы по величине. Под воздействием сигнала ошибки СС луч антенны РЛС периодически то устремляется к нулевому углу места, то, при достижении сдвига фаз между сигналами в 180°, снова движется вверх по направлению к НЛЦ [«Справочник по радиолокационным измерениям». Д. Бартон, Г. Вард. Москва, «Советское радио», 1976 г.]. При этом сигнал СС образует локальные максимумы, так называемые «колокола».
Известны следующие способы определения высоты полета НЛЦ [А.И. Леонов, К.И. Фомичев. «Моноимпульсная радиолокация». Москва, «Радио и связь», 1984 г.].
Для борьбы с явлением многопутного распространения при сопровождении НЛЦ используются различные методы, которые можно условно разделить на две группы.
К первой относятся методы, направленные на создание узконаправленных по углу места ДН антенн с целью уменьшения (или исключения) проникновения сигнала «антипода» в главный луч ДН антенны. Практическая реализация этих способов подразумевает увеличение апертуры антенной системы по вертикали и по горизонтали. Повышение угловой разрешающей способности лежит в основе этих способов. Реализация крупногабаритных антенн затруднительна для большинства передвижных радиолокаторов, предназначенных для обнаружения и сопровождения НЛЦ, так как повышается конструктивно-технологическая сложность систем и снижается их мобильность.
Вторая группа способов определения угла места (высоты НЛЦ) основана на использовании дополнительной информации о влиянии отражений от подстилающей поверхности и устранении или уменьшении этого влияния на оценку угла места (высоты) НЛЦ. К этому подклассу относится большое число методов, основанных на моноимпульсном методе измерения угломестной координаты. Моноимпульсные способы измерения угла места НЛЦ имеют преимущества, как наиболее устойчивые к шумовым и динамическим ошибкам измерения.
В работе [А.И. Леонов, К.И. Фомичев. «Моноимпульсная радиолокация». Москва, «Радио и связь», 1984 г.] описан способ определения угла места НЛЦ, при котором используются две антенны в вертикальной плоскости, расположенные на разной высоте. Антенны имеют идентичные ДН и одинаковую ориентацию по углу места. Расстояние между антеннами регулируется так, чтобы разность фаз между сигналами от «антипода», принимаемых двумя антеннами, равнялась π. При этом разность фаз между сигналами от НЛЦ должна быть отлична от π. В зависимости от амплитуды и фазы сигналов (от НЛЦ и «антипода»), принятых антеннами, вырабатываются сигналы управления сдвигом фазы сигнала (от НЛЦ и антипода) и разнесением антенн по высоте. Если сигнал ошибки от НЛЦ и управляющий сигнал разнесения антенн одновременно равняются нулю, то система отслеживает направление на НЛЦ со сравнительно малыми ошибками. Указанный способ, несмотря на высокую точность определения угла места НЛЦ, весьма сложен в конструктивном отношении, требует использования дополнительной антенны.
Наиболее близким по технической сущности к заявляемому способу является способ вычисления высоты полета НЛЦ, описанный в [патент RU №2080619 С1, МПК G01S 13/44. Способ определения угла места и дальности низколетящей цели моноимпульсным радиолокатором при многолучевом распространении отраженного от цели сигнала. 1994 г.], характеризующийся формированием и излучением зондирующих радиолокационных сигналов, приемом отраженных эхо-сигналов от НЛЦ и от подстилающей поверхности (сигнала «антипода») и их обработкой с помощью ЭВМ РЛС для определения угла места НЛЦ без размыкания контура СС по углу места.
Недостатком прототипа является то, что этот способ работает тогда, когда известно, что рассматривается 1-ый нуль мнимой функции (Im), то есть набег фаз в 180° между прямым сигналом от НЛЦ и сигналом «антипода» произошел только один раз. Для последующих нулей мнимой функции (Im) этот способ работать не будет из-за неоднозначности вычислений. Кроме того, для реализации этого способа необходимо организовывать дополнительную квадратурную обработку принимаемого сигнала в угломестном канале, и возникает необходимость изменения высоты антенны РЛС.
Недостатками прототипа являются также невозможность по результатам одного зондирования РЛС, то есть в реальном масштабе времени, определять истинный угол места НЛЦ и высоту ее полета, а также отсутствие привязки РЛС по координатам и по высоте относительно уровня моря и к системе единого времени (СЕВ).
Особенностью заявляемого способа является то, что в нем не снижается отрицательное влияние явления многолучевости на характер сигнала СС, а угол места НЛЦ и высота ее полета определяются в любой момент сопровождения НЛЦ в любой точке конкретного локального максимума или минимума сигнала СС по углу места - «колокола», вызванного проникновением сигнала «антипода» в главный луч ДН антенны. Предлагаемый способ не требует изменения высоты антенны РЛС и основан на определении угла «антипода», разности фаз между прямым сигналом и сигналом «антипода» и коэффициента отражения от подстилающей поверхности как функций одной переменной - угла места цели. Это дает возможность при использовании данных сопровождения НЛЦ, поступающих с приемного устройства РЛС на данном такте зондирования, и значений параметров антенной системы РЛС вычислить значения векторов прямого сигнала и сигнала «антипода» и определить значения фазы вектора суммарного канала и фазы вектора угломестного разностного канала. Затем, путем сравнения полученных значений фаз с контрольными значениями фазы сигнала в суммарном канале и фазы сигнала в угломестном разностном канале определяются истинный угол места НЛЦ и высота ее полета. Высота полета НЛЦ определяется без общепринятого прямого измерения угла места этой НЛЦ, выполняемого с помощью относительно сложных парциальных узконаправленных по углу места антенн или с использованием отдельного РЛС-высотомера и др. Вместо этого в данном способе применяется значительно более простая 4-квадрантная антенна, которая используется в СС РЛС по углу места и в наклонной плоскости.
Техническим результатом изобретения является устранение недостатков прототипа - более точное определение высоты полета НЛЦ при одновременном упрощении конструкции антенной системы РЛС, путем учета при определении высоты НЛЦ расширенных данных, влияющих на ее точность, полученных до начала развертывания РЛС в точке дислокации (точные координаты, в том числе высота РЛС относительно уровня моря) и при радиолокационном сопровождении НЛЦ в реальном масштабе единого времени (отраженных радиолокационных сигналов от НЛЦ и от подстилающей поверхности) при учете фазовых соотношений между прямым сигналом и сигналом «антипода», позволяющие более точно измерять дальность до НЛЦ и, как следствие, ее высоту.
Заявляемый способ позволяет по результатам одного зондирования РЛС в любой момент сопровождения НЛЦ, то есть в реальном масштабе времени, определять истинный угол места НЛЦ и высоту ее полета.
Кроме того, в заявляемом способе не требуется проведение каких-либо конструктивных или аппаратурных изменений в РЛС, введения дополнительной квадратурной обработки, изменения высоты антенны РЛС и т.д.
В заявляемом способе точность определения высоты полета НЛЦ в основном определяется точностью определения дальности до цели, которая поступает от РЛС при сопровождении, точностью поступающих значений синусов углов отклонения луча РЛС в угломестной и в наклонной плоскостях, точностью поступающего контрольного значения фазы сигнала в суммарном канале, точностью поступающего контрольного значения фазы сигнала в угломестном канале, точностью поступающих значений амплитуд сигналов в суммарном канале, угломестном и азимутальном разностных каналах.
Указанный технический результат достигается тем, что используется способ определения высоты полета НЛЦ моноимпульсной РЛС сопровождения в реальном масштабе времени, характеризующийся формированием и излучением зондирующих радиолокационных сигналов, приемом отраженных эхо-сигналов от НЛЦ и от подстилающей поверхности и их обработкой с помощью ЭВМ РЛС для определения дальности до НЛЦ, определения высоты ее полета и соответствующего взаимного геометрического расположения РЛС и НЛЦ. Особенностью этого способа является то, что в РЛС используется антенна с 4-мя квадрантами А, В, С, D полотна, реализующими суммарно-разностную обработку по углу места и в наклонной плоскости. Рассматриваемый способ основан на вычислении угла «антипода», разности фаз между прямым сигналом и сигналом «антипода» и коэффициента отражения от подстилающей поверхности как функций одной переменной -угла места. Это дает возможность при использовании данных сопровождения НЛЦ, поступающих с приемного устройства РЛС на данном такте зондирования, и значений параметров антенной системы РЛС вычислять значения векторов прямого сигнала и сигнала «антипода» и определять значения фазы вектора суммарного канала и фазы вектора угломестного разностного канала. В процессе проводимого одномерного поиска по углу места путем сравнения вычисляемых значений фаз с контрольным значением фазы сигнала в суммарном канале и с контрольным значением фазы сигнала в угломестном разностном канале определяются истинный угол места НЛЦ и высота ее полета.
Способ осуществляется в 2 последовательных этапа:
на 1-м этапе, после развертывания РЛС в точке ее дислокации в память ЭВМ РЛС вводятся точные координаты места дислокации РЛС, в том числе, по высоте относительно уровня моря, точное время системы единого времени (СЕВ) с помощью входящего в РЛС спутникового навигатора с атомными часами,
на 2-м этапе, с помощью РЛС осуществляют сопровождение НЛЦ, при этом вычисления выполняются в реальном масштабе времени, то есть они выполняются на каждом такте зондирования РЛС.С приемного устройства РЛС на программу ЭВМ РЛС вычисления высоты НЛЦ поступают следующие исходные данные:
текущие координаты НЛЦ X, Y, Z;
амплитуды сигналов в суммарном канале AΣ, угломестном АЕ и азимутальном АВ разностных каналах;
синусы углов отклонения луча РЛС ϕВ и ϕН в угломестной и наклонной плоскостях sin ϕВ и sin ϕН;
контрольное значение фазы сигнала в суммарном канале Ф_Sum;
контрольное значение фазы сигнала в угломестном разностном канале Ф_Е;
длина рабочей волны РЛС λ метрового, дециметрового или сантиметрового диапазона.
Вычисления выполняются в следующей последовательности.
Вычисляется значение горизонтальной дальности RГ НЛЦ:
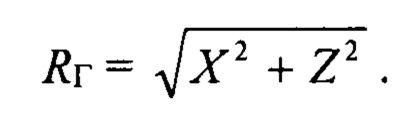
Вычисляется косинус суммарного угла отклонения луча РЛС θХ от нормали к антенному полотну:
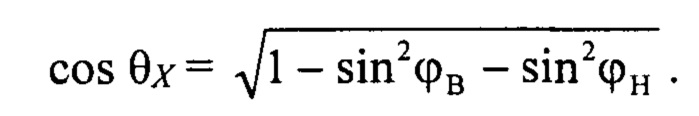
Вычисляется угол положения центра луча радиолокатора εЛ:
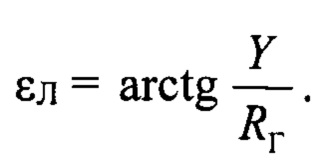
Вычисляется отношение амплитуд сигналов в суммарном канале и азимутальном разностном канале KΣ_В.
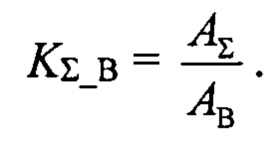
Вычисляется необходимая расстройка по азимуту B1:
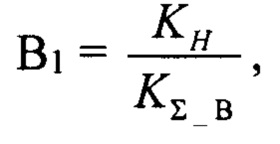
где КН - нормирующий коэффициент.
Вычисляется сигнал в угломестном разностном канале:
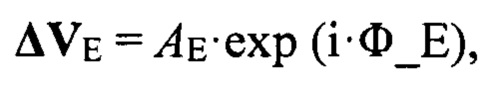
где i - мнимая единица.
Вычисляются сигналы в суммах квадрантов (А+В) и (С+D) SumАB и SumCD:
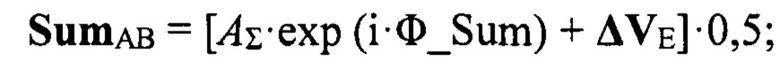
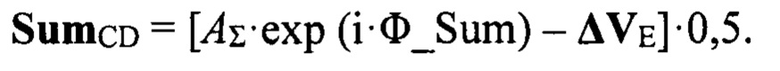
Вычисляется контрольное значение разности фаз Δ_ϕABCD между суммами квадрантов полотна (А+В) и (С+D):
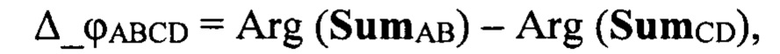
где Arg(…) - функция вычисления аргумента комплексной величины.
Формула для вычисления угла «антипода» β для «плоской» Земли как функции угла места цели ε имеет вид:
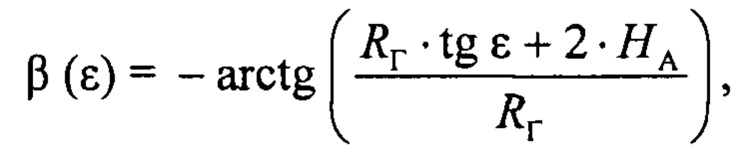
где НA - высота фазового центра антенны РЛС.
Формула для вычисления сдвига по фазе δ между прямым сигналом и сигналом «антипода» как функции угла места цели ε имеет вид:
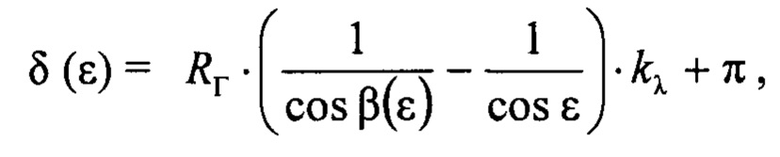
где kλ=2⋅π/λ -модуль волнового вектора;
π - дополнительный сдвиг фазы при отражении. Случайная фаза ΔϕСЛУЧ, возникающая из-за интерференции сигналов, отраженных от блестящих точек цели, не учитывается, так как из-за большой дальности характер отражения от блестящих точек цели для прямого сигнала и сигнала «антипода» практически идентичен, и добавка по фазе ΔϕСЛУЧ почти одинакова для обоих сигналов. Формулы для вычисления прямых сигналов (векторов) от НЛЦ в квадрантах полотна антенны А, В, С, D в векторной форме имеют вид:
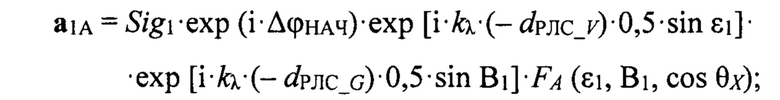
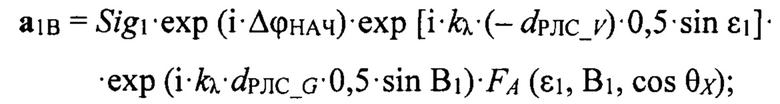
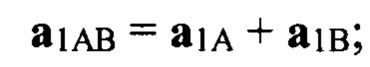
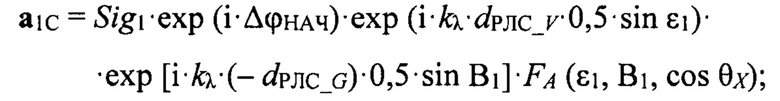
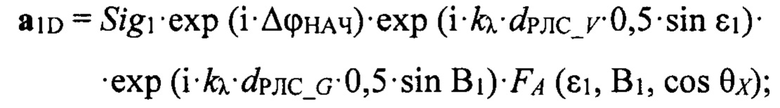
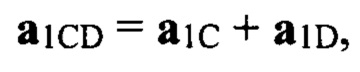
где Sig1 - величина прямого сигнала (модуль вектора сигнала) от цели, Sig1=1;
dРЛС_V, dРЛС_G - базы антенны РЛС для угломестного и азимутального разностных каналов, при вычислении значения dРЛС_V учитывается фактическое уменьшение базы антенны РЛС в угломестной плоскости из-за угла отклонения луча РЛС в уг-ломестной плоскости от нормали к полотну антенны ϕB;
угол ε1=ε - εЛ;
i -мнимая единица;
FА (ε1, B1, cos θХ) - функция ДН одного квадранта антенны РЛС, главный лепесток которой аппроксимируется функцией вида 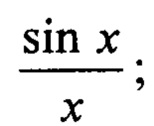
ΔϕНАЧ - неизвестная начальная фаза сигнала, принимается ΔϕНАЧ=0, так как начальная фаза входит во все сигналы всех квадрантов полотна антенны. Формулы для вычисления сигналов (векторов) «антипода» в квадрантах полотна антенны А, В, С, D имеют вид:
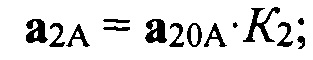
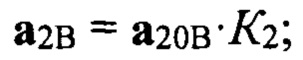
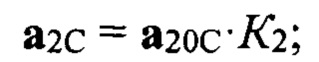
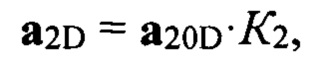
где К2 - коэффициент отражения от подстилающей поверхности, который реализовался на данном такте зондирования. Формулы для вычисления сигналов (векторов) а20А, а20В, а20С, а20D в векторной форме имеют вид:
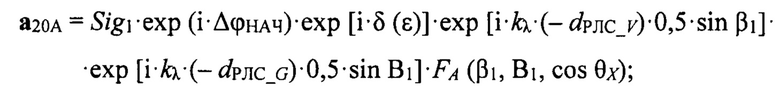
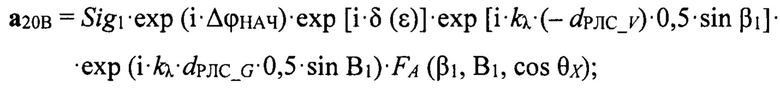
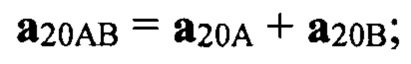
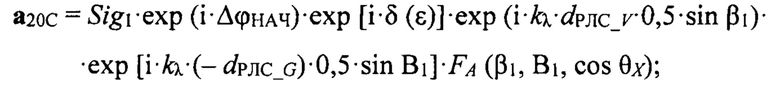
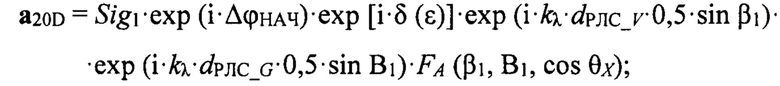
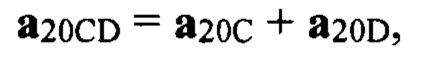
где δ (ε) - сдвиг по фазе между прямым сигналом и сигналом «антипода»;
угол β1=β - εЛ;
FА (β1, B1, cos θХ) - функция ДН одного квадранта антенны РЛС, главный лепесток которой аппроксимируется функцией вида 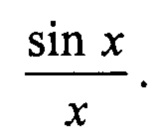 С применением формулы тангенса разности двух углов получена формула квадратного уравнения для вычисления коэффициента отражения К2.
С применением формулы тангенса разности двух углов получена формула квадратного уравнения для вычисления коэффициента отражения К2.
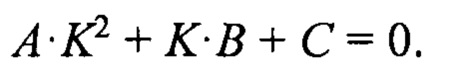
Формулы для вычисления коэффициентов А, В, С имеют вид:
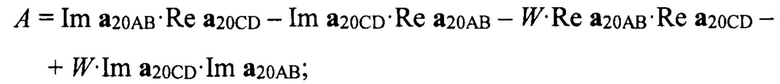
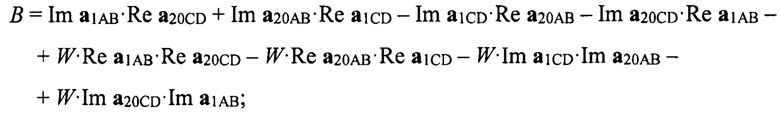
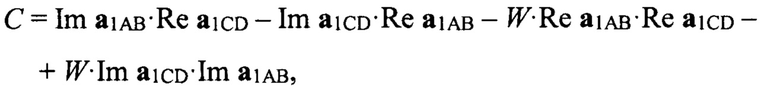
где Re…, Im… - действительные и мнимые части соответствующих векторов a1AB, a1СD, а20АВ, а20СD;
W - тангенс контрольного значения разности фаз Δ_ϕABCD: W=tg Δ_ϕABCD. Коэффициент К2=-1, если дискриминант квадратного уравнения В2 - 4⋅А⋅С<0. Неверный корень квадратного уравнения отбрасывается исходя из условия, что коэффициент отражения К2 может быть только положительным и меньшим единицы (0<K2<1). Формулы для вычисления угла β «антипода», сдвига по фазе δ между прямым сигналом и сигналом «антипода» и коэффициента отражения от подстилающей поверхности К2 на данном такте зондирования получены в виде функций одной переменной, а именно угла места ε. После этого вычисляется фаза вектора суммарного канала Arg_Sum и фаза вектора угломестного разностного канала Arg_E:
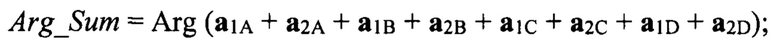
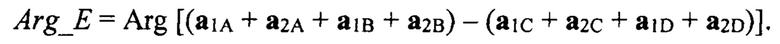
Затем для селекции ложных углов места и определения истинного угла места НЛЦ во всем угловом диапазоне углов места ε начиная от 0° и до значения ширины суммарной ДН антенны РЛС по уровню 0,5 выполняется одномерный поиск глобального минимума модуля фазы вектора суммарного канала Arg_Sum относительно контрольного значения фазы Ф_Sum и фазы вектора угломестного разностного канала Arg_E относительно контрольного значения фазы Ф_Е. Формула для вычисления функции модуля указанных величин имеет вид:
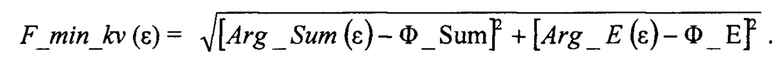
Глобальный минимум функции F_min_kv (ε) определяет значение истинного угла места НЛЦ εИСТ, его вычисляемый коэффициент отражения К2 и высоту полета НЛЦ HЦ:
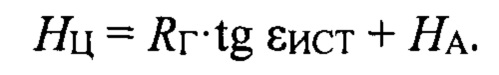
На фиг. 1-5 соответственно представлены:
фиг. 1 - характерный вид локальных максимумов сигнала СС по углу места («колокола» сигнала СС по углу места), истинный угол места НЛЦ, минимумы модуля сигнала угломестного разностного канала;
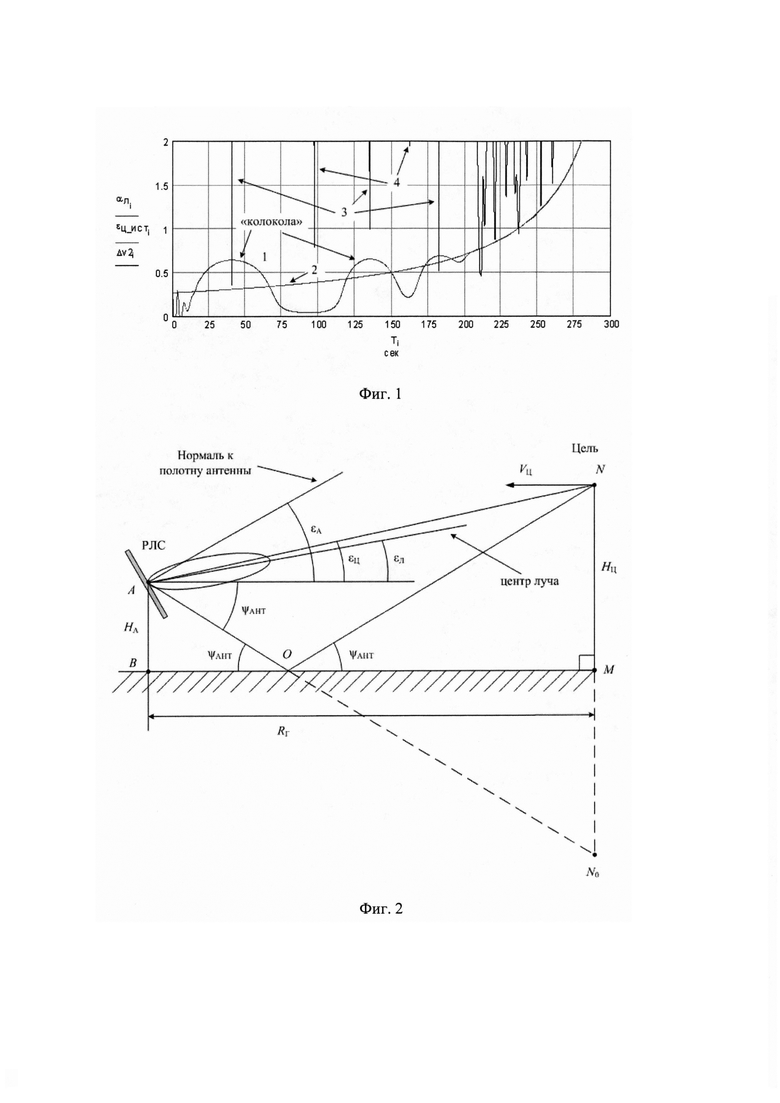
фиг. 2 - геометрия распространения прямого луча и луча, отраженного от Земли для «плоской» Земли;
фиг. 3 - классический вид квадратного полотна антенны моноимпульсной РЛС;
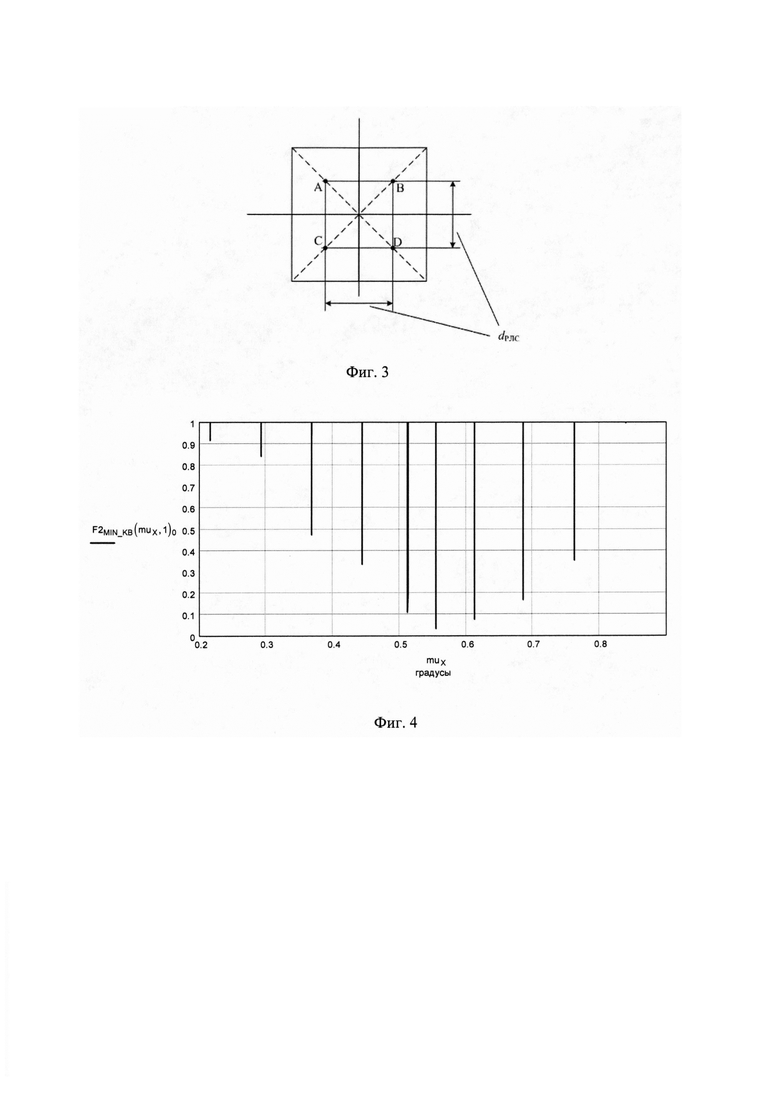
фиг. 4 - кривые минимумов, полученные при выполнении одномерного поиска минимума функции вычисления модуля F_min_kv (ε) во всем угловом диапазоне углов места;
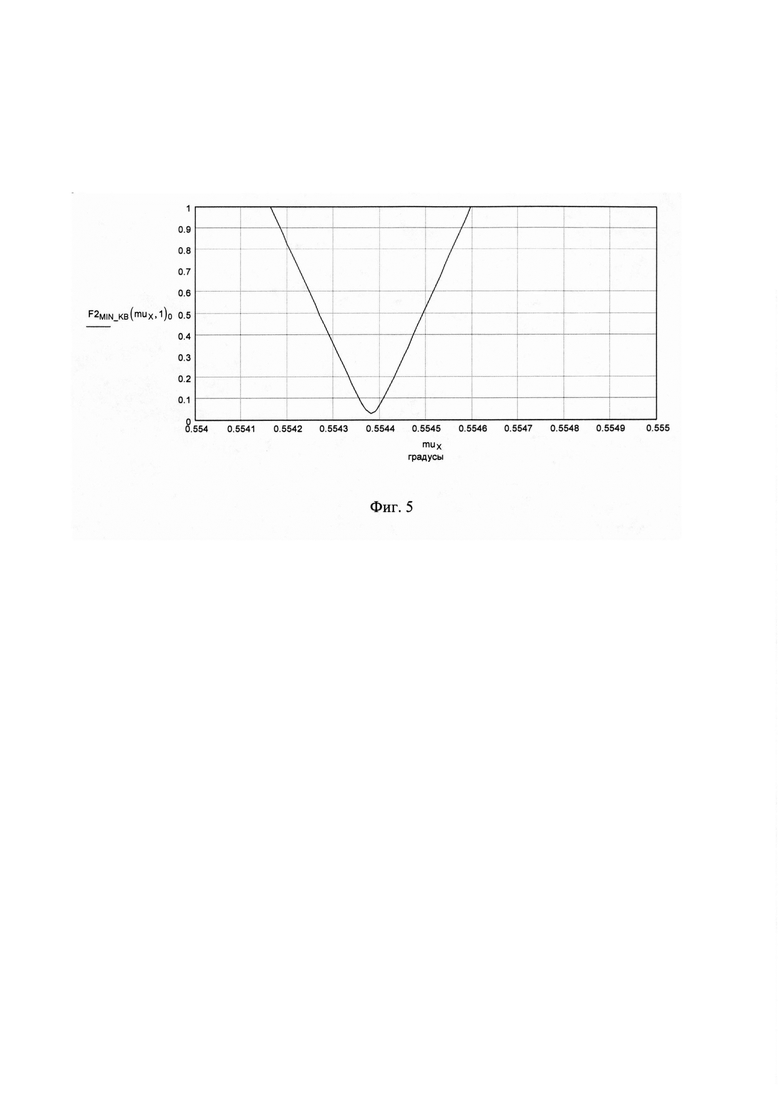
фиг. 5 - глобальный минимум функции вычисления модуля F_min_kv (ε), определяющий значение истинного угла места НЛЦ εИСТ и высоту полета НЛЦ HЦ.
На фиг. 1 обозначено: кривая 1 - сигнал СС по углу места в градусах; кривая 2 - изменение истинного угла места НЛЦ в градусах; кривые 3 - минимумы модуля сигнала в угломестном разностном канале, соответствующие центрам «колоколов» и разности фаз между сигналами в 180°; кривые 4 -минимумы модуля сигнала в угломестном разностном канале, соответствующие разности фаз между сигналами в 0°. По оси абсцисс отложено время в секундах. По оси ординат отложены градусы.
На фиг. 2 обозначено: НА - высота фазового центра антенны РЛС; εА - угол поднятия нормали к полотну антенны РЛС относительно горизонта; εЦ - истинный угол места НЛЦ; εЛ - угловое положение центра луча РЛС; HЦ - высота полета НЛЦ; VЦ - скорость полета НЛЦ; ψАНТ - угол скольжения сигнала «антипода»; RГ - горизонтальная дальность до НЛЦ; А -положение фазового центра антенны РЛС; О - точка отражения сигнала «антипода»; N - положение НЛЦ; N0 - зеркальное положение НЛЦ.
На фиг. 3 обозначено: А, В, С, D -квадранты полотна антенны моноимпульсной РЛС; dРЛС -база антенны РЛС.
На фиг. 4 по оси абсцисс отложены градусы. По оси ординат отложены градусы.
На фиг. 5 по оси абсцисс отложены градусы. По оси ординат отложены градусы.
Сущность заявляемого изобретения состоит в следующем.
Особенностью заявляемого способа является то, что в нем не снижается отрицательное влияние явления многолучевости на характер сигнала СС, и угол места НЛЦ (и высота ее полета) определяется в любой момент сопровождения НЛЦ в любом месте конкретного локального максимума или минимума сигнала СС по углу места - «колокола», вызванного проникновением сигнала «антипода» в главный луч ДН антенны. Предлагаемый способ не требует изменения высоты антенны РЛС и основан на вычислении угла «антипода», разности фаз между прямым сигналом и сигналом «антипода» и коэффициента отражения от подстилающей поверхности как функций одной переменной, а именно угла места. Для выполнения этих вычислений используются данные сопровождения НЛЦ, поступающие с приемного устройства РЛС на данном такте зондирования, и значения параметров антенной системы РЛС.При этом на данном такте зондирования вычисляются значения векторов прямого сигнала и сигнала «антипода» и определяются значения фазы вектора суммарного канала и фазы вектора угломестного разностного канала. Затем для селекции ложных углов места и определения истинного угла места НЛЦ во всем угловом диапазоне углов места начиная от нулевого значения и до значения ширины суммарной ДН антенны РЛС выполняется одномерный поиск минимума вычисляемого модуля фазы вектора суммарного канала относительно контрольного значения фазы сигнала в суммарном канале и фазы вектора угломестного разностного канала относительно контрольного значения фазы сигнала в угломестном разностном канале. Контрольные значения фаз сигналов в суммарном канале и в угломестном разностном канале поступают с приемного устройства РЛС. Полученный глобальный минимум определяет истинный угол места НЛЦ и высоту ее полета. Высота полета НЛЦ определяется без общепринятого прямого измерения угла места этой НЛЦ, выполняемого с помощью относительно сложных парциальных узконаправленных по углу места антенн или с использованием отдельного РЛС-высотомера и др., вместо чего в данном способе применяется значительно более простая 4-квадрантная антенна, которая используется в СС РЛС по углу места и в наклонной плоскости.
Способ осуществляется следующим образом.
Рассмотрим простейшую РЛС сопровождения, которая имеет 4-х квадрантную антенну с возможностью поворота ее на любой угол по азимуту, согласно полученному целеуказанию. При этом ДН этих квадрантов синхронно управляются. После развертывания РЛС в точке ее дислокации осуществляется ее координатная привязка к единой системе координат ПВО страны с помощью входящего в состав РЛС спутникового навигатора.
Способ осуществляется в 2 последовательных этапа.
На 1-м этапе, после развертывания РЛС в точке ее дислокации в память ЭВМ РЛС вводятся с помощью соответствующего пульта точные координаты места дислокации РЛС, в том числе, по высоте относительно уровня моря, точное время СЕВ с помощью входящего в РЛС спутникового навигатора с атомными часами.
На 2-м этапе, после включения РЛС осуществляют с ее помощью радиолокационную работу в выделенном секторе ответственности, в том числе принятие целеуказания о наличии НЛЦ или нескольких НЛЦ, получение необходимых данных об НЛЦ и фиксирование их в памяти ЭВМ РЛС для вычисления высоты НЦ НЛЦ.
Рассмотрим подробнее осуществление способа на 2-м этапе. К основному каналу получения радиолокационной информации (эхо-сигналы, отраженные от НЛЦ и подстилающей поверхности и др.) относятся, в частности, 4-х квадрантная антенна и следящая система (СС) РЛС по углу места и по азимуту. При этом СС формирует упреждающий строб автосопровождения НЛЦ.
При работе РЛС очередной «колокол» начинает формироваться при приближении разности фаз между сигналом от НЛЦ и сигналом «антипода» к 180°. В моменты максимумов «колоколов» (см. фиг. 1) разность фаз между сигналом от НЛЦ и сигналом «антипода» становится равной 180°. Так как сигналы близки по мощности, то сигнал суммарного канала стремится к нулю. Модуль сигнала в угломестном разностном канале Δε также стремится к нулю. Поэтому при вычислении сигнала ошибки Де фазового дискриминатора (ФД) выполняется деление на ноль, то есть возникает сингулярность.
Из-за явления сингулярности вычисляемая угловая ошибка Δε в угломестном канале может достигать очень большой величины, которую будет ограничивать только собственный шум суммарного канала. СС резко увеличивает угол подъема луча εЛ, и образуются «колокола» (см. фиг. 1).
В моменты максимумов «колоколов» (см. фиг. 1) разность фаз между сигналом от НЛЦ и сигналом «антипода» становится равной 180°. Между каждыми соседними локальными максимумами сигнала СС («колоколами») разность хода между сигналами ΔL возрастает на длину рабочей волны РЛС λ, или, что то же самое, разность фаз сигналов увеличивается на 2⋅π. Эти локальные максимумы («колокола») хорошо различимы при сопровождении НЛЦ.
С течением времени период следования «колоколов» уменьшается, так как при увеличении угла места НЛЦ εЦ разность хода ΔL (и разность фаз) между прямым сигналом и сигналом «антипода» возрастает все быстрее (см. фиг. 2).
Например, на фиг. 1 приведен вид локальных максимумов сигнала СС по углу места εЛ («колоколов») для плоской Земли и гладкой поверхности -кривая 1, при этом истинный угол места НЛЦ - кривая 2. Высота полета НЛЦ НЦ=200 м, скорость полета НЛЦ VЦ=130 м/с, полетное время (время наблюдения НЛЦ) отложено по оси абсцисс, коэффициент отражения от подстилающей поверхности ρ ≈ 0,9, длина рабочей волны РЛС λ=0,03 м.
В выбранный момент времени на 2-м этапе осуществления способа вычисляется высота полета HЦ НЛЦ. При этом используются данные, зафиксированные в памяти ЭВМ на 1-м этапе. Для пояснения достаточно сложного алгоритма вычисления уточним некоторые его моменты.
На фиг. 2 представлена геометрия распространения прямого луча и луча, отраженного от земной поверхности («антипода») для «плоской» Земли.
На фиг. 3 приведено классическое квадратное полотно антенны РЛС (А, В, С, D - квадранты полотна). Суммарно-разностная обработка выполняется по схеме Пейджа. Угломестный разностный канал формируется стандартным образом: (SigA+SigВ) -(SigС+SigD), где SigA, SigB, SigС, SigD - сигналы с квадрантов А, В, С, D.
В простейшем варианте работы СС по углу места положение центра луча радиолокатора ел на i+1 - м шаге описывается формулой:

где Dε - добротность СС (коэффициент усиления сигнала ошибки);
εЛi -положение луча на i-м шаге;
Δεi - сигнал ошибки фазового дискриминатора (ФД) угломестного канала на i - м шаге;
Δt - величина такта зондирования.
Выполним определение высоты полета НЛЦ с помощью предлагаемого способа.
Вычисления выполняются в реальном масштабе времени, то есть они выполняются на каждом такте зондирования РЛС. На некотором i-ом такте работы (такте зондирования) с приемного устройства РЛС на программу ЭВМ РЛС вычисления высоты НЛЦ поступают следующие исходные данные:
текущие координаты НЛЦ X, Y, Z;
амплитуды сигналов в суммарном канале АΣ, угломестном АE и азимутальном АB разностных каналах;
синусы углов отклонения луча РЛС ϕB и ϕH в угломестной (вертикальной) и наклонной плоскостях sin ϕB и sin ϕH;
контрольное значение фазы сигнала в суммарном канале Ф_Sum;
контрольное значение фазы сигнала в угломестном разностном канале Ф_Е;
длина рабочей волны РЛС λ метрового, дециметрового или сантиметрового диапазона.
Вычисления выполняются в следующей последовательности.
Значение горизонтальной дальности RГ вычисляется по формуле:

Вычисляется косинус суммарного угла отклонения луча от нормали θХ:
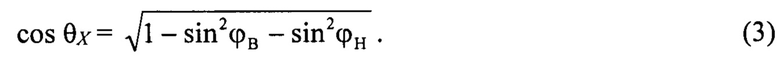
Вычисляется угол положения центра луча радиолокатора εЛ:

Вычисляется отношение амплитуд сигналов в суммарном канале и азимутальном разностном канале KΣ_В:

Вычисляется необходимая расстройка по азимуту B1, которая затем используется в функции ДН одного квадранта антенны РЛС:

где КН - нормирующий коэффициент.
Сигнал в угломестном разностном канале записывается в виде:

где i -мнимая единица.
Вычисляются сигналы в суммах квадрантов (А+В) и (С+D) SumAB и SumCD:
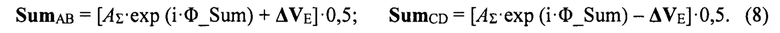
С помощью полученных данных вычисляется контрольное значение разности фаз Δ_ϕАВСD между суммами квадрантов полотна (А+В) и (С+D):
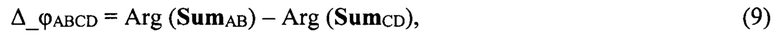
где Arg(…) - функция вычисления аргумента комплексной величины.
Угол ε - угол места цели, ε=εЦ (см. фиг. 2); угол β - угол «антипода», это отрицательный угол, β=ψАНТ, ψАНТ - угол скольжения (см. фиг. 2). Для «плоской» Земли угол β является функцией угла ε и вычисляется по формуле:
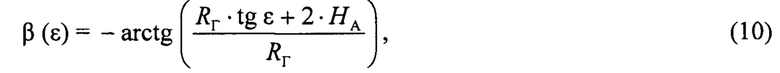
где НА - высота фазового центра антенны РЛС;
RГ - горизонтальная дальность до цели.
Сдвиг по фазе δ между прямым сигналом и сигналом «антипода» вычисляется по формуле:
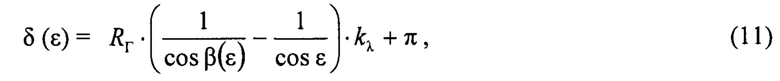
где kλ=2⋅π/λ - модуль волнового вектора;
λ - длина рабочей волны РЛС метрового, дециметрового или сантиметрового диапазона;
π - дополнительный сдвиг фазы при отражении [«Справочник по радиолокации в 4 томах, т.1», под. ред. М.И. Сколника. Москва, «Советское радио», 1976 г., «Справочник по радиолокации в 2 книгах», под. ред. М.И. Сколника. Москва, «Техносфера», 2014 г., Lamont V.Blake, "Machine Plotting of Radio/Radar Vertical-Plane Coverage Diagrams". Naval Research Laboratory, Washington, D. C., 1970].
Необходимо отметить, что к сдвигу по фазе δ (11) будет добавляться некоторая случайная фаза ΔϕСЛУЧ, возникающая из-за интерференции сигналов, отраженных от блестящих точек цели. Однако эта случайная фаза ΔϕСЛУЧ добавляется как в прямой сигнал, так и в сигнал «антипода», так как из-за большой дальности углы на цель и на «антипод» практически одинаковы, и характер отражения от блестящих точек цели для обоих сигналов будет практически идентичным. Эта добавка по фазе ΔϕСЛУЧ почти одинакова для обоих сигналов. Таким образом, для случая сопровождения НЛЦ, можно не рассматривать случайную фазу ΔϕСЛУЧ отдельно, а считать, что она добавляется к неизвестной начальной фазе сигнала ΔϕНАЧ.
Прямые сигналы (векторы) от НЛЦ в квадрантах полотна антенны А, В, С, D записываются в векторном (комплексном) виде:
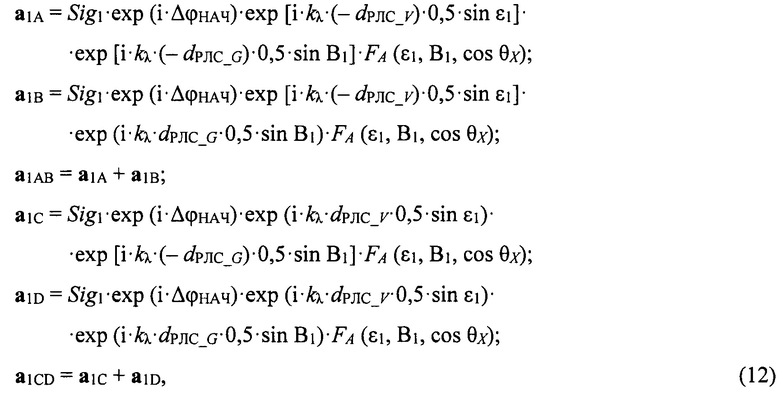
где Sig1 - величина прямого сигнала (модуль вектора сигнала) от цели, она неизвестна, Sig1=1;
dРЛС_V, dРЛС_G - базы антенны РЛС для угломестного и азимутального разностных каналов, при вычислении значения dРЛС_V учитывается фактическое уменьшение базы антенны РЛС в угломестной (вертикальной) плоскости из-за угла отклонения луча РЛС в угломестной плоскости от нормали к полотну антенны ϕB (см. фиг. 2);
угол ε1=ε-εЛ;
FА (ε1, B1, cos θХ) - функция ДН одного квадранта антенны РЛС, главный лепесток которой аппроксимируется функцией вида 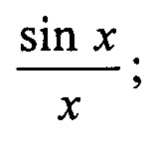
i - мнимая единица;
ΔϕНАЧ - неизвестная начальная фаза сигнала, которую можно считать равной 0, так как начальная фаза входит во все сигналы всех квадрантов полотна антенны: ΔϕНАЧ=0.
Сигналы (векторы) «антипода» в квадрантах полотна антенны А, В, С, D записываются в виде:

где К2 - это коэффициент отражения от подстилающей поверхности, который реализовался на данном такте зондирования.
Из-за влияния различных неровностей подстилающей поверхности (трава, кусты, деревья и т.п.) коэффициент отражения К2 может значительно изменяться от такта к такту. Поэтому «колокола» в реальной работе РЛС обычно имеют хаотический, местами рваный характер.
Сигналы (векторы) а20А, а20В, а20С, а20D записываются в векторном (комплексном) виде:
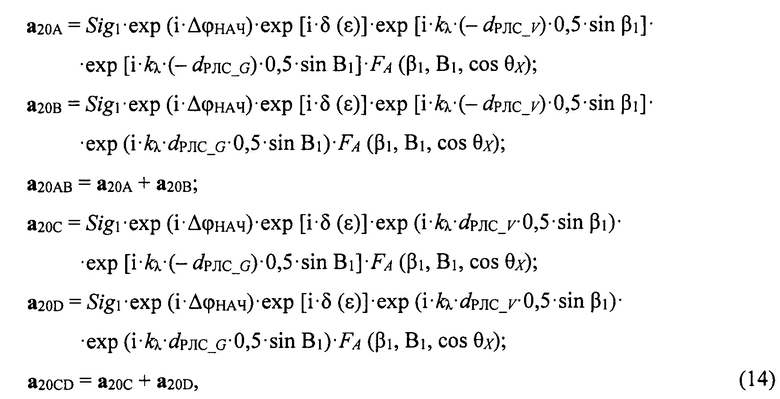
где δ(ε) - сдвиг по фазе между прямым сигналом и сигналом «антипода» (11);
угол β1=β - εЛ;
FА (β1, B1, cos θХ) - функция ДН одного квадранта антенны PЛС, главный лепесток которой аппроксимируется функцией вида 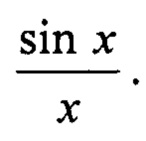
Применяя выражение для тангенса разности двух углов:
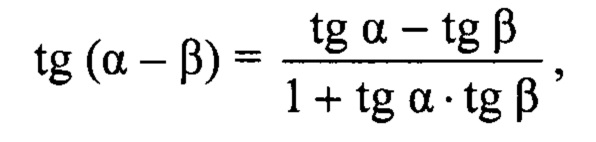
получаем формулу для непосредственного вычисления коэффициента отражения К2, реализовавшегося на данном такте зондирования. Коэффициент отражения от подстилающей поверхности Кг является корнем квадратного уравнения:

где коэффициенты А, В, С вычисляются по формулам:

Здесь Re…, Im… - действительные и мнимые части соответствующих векторов a1AB, a1СD, а20АВ, а20СD;
W - тангенс контрольного значения разности фаз Δ_ϕABCD: W=tg Δ_ϕABCD.
Если дискриминант уравнения (15) В2-4⋅А⋅С<0, то коэффициент К2=-1.
Из физических условий задачи известно, что коэффициент отражения Кг может быть только положительным и меньшим единицы (0<К2<1). Исходя из этого условия, отбрасывается неверный корень уравнения (15).
Получена формула вычисления коэффициента отражения от подстилающей поверхности К2 для произвольного значения угла места ε.
Таким образом, угол β (ε) на «антипод» (10), сдвиг по фазе δ(ε) между прямым сигналом и сигналом «антипода» (11) и коэффициент отражения от подстилающей поверхности К2 (15) на данном такте зондирования определяются в виде функций одной переменной, а именно угла места ε.
Применяя формулы записи векторов сигналов в квадрантах полотна антенны А, В, С, D (12÷14), вычисляем фазу вектора суммарного канала Arg_Sum и фазу вектора угломестного разностного канала Arg_E:
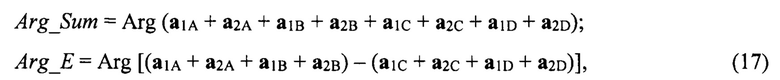
где Arg(…) - функция вычисления аргумента комплексной величины.
Для селекции ложных углов места и определения истинного угла места НЛЦ во всем угловом диапазоне углов места 8 начиная от 0° и до значения ширины суммарной ДН антенны РЛС по уровню 0,5 (θ0,5) выполняется одномерный поиск глобального минимума модуля фазы вектора суммарного канала Arg_Sum (17) относительно контрольного значения фазы Ф_Sum и фазы вектора угломестного разностного канала Arg_E (17) относительно контрольного значения фазы Ф_Е.
Функция вычисления модуля указанных величин имеет вид:
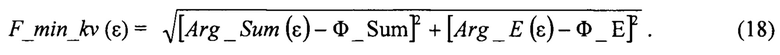
Использование функции вычисления оптимума в таком виде (18) позволяет минимизировать влияние возможных ошибок при передаче в программу исходных данных сопровождения НЛЦ.
Глобальный минимум функции F_min_kv (ε) (18) определяет значение истинного угла места НЛЦ εИСТ, его вычисляемый коэффициент отражения К2 и высоту полета НЛЦ HЦ:

Так выполняется селекция ложных углов места и определяется истинный угол места НЛЦ εИСТ и высота полета НЛЦ НЦ.
Предлагаемый способ основан на однозначном соответствии истинному углу места εИСТ исходных данных, получаемых от РЛС на данном такте зондирования: координат НЛЦ X, Y, Z, амплитуд сигналов в суммарном канале AΣ, угломестном АЕ и азимутальном АВ разностных каналах, контрольного значения фазы сигнала в суммарном канале Ф_Sum, контрольного значения фазы сигнала в угломестном разностном канале Ф_Е, значений синусов углов отклонения луча РЛС ϕB и ϕH в угломестной и в наклонной плоскостях - sin ϕB и sin ϕH. Для всех других анализируемых углов ε (так как обычно присутствуют локальные минимумы от ложных углов) соответствующая ошибка, то есть значение минимума функции вычисления модуля F_min_kv(ε) (18), возрастает, как при увеличении угла, так и при уменьшении угла относительно истинного угла места εИСТ.
Рассмотрим осуществление способа при следующих исходных данных.
Высота полета НЛЦ НЦ=200 м, скорость НЛЦ VЦ=55 м/с. Контрольное значение фазы сигнала в суммарном канале Ф_Sum=0°, контрольное значение фазы сигнала в угломестном разностном канале Ф_Е=240,47°. Эффективная поверхность рассеяния НЛЦ σЦ≈2 м2. Отношение сигнал/шум ρСШ≈35дБ.
Значения баз антенны РЛС для угломестного и азимутального разностных каналов dРЛС_V=0,7398 м (с учетом фактического уменьшения базы антенны РЛС в угломестной плоскости из-за отклонения луча РЛС в угломестной плоскости от нормали к полотну антенны на угол ϕB ≈ 29,49°), dРЛС_G=0,85 м. Рабочая длина волны РЛС λ=0,03 м. Добротность СС Dε=5, величина такта зондирования Δt=0,1 с. Угол отклонения нормали к полотну антенны от горизонтали εA=30°. Высота фазового центра антенны НA=5,5 м. Ширина ДН одного квадранта θ0,5 ≈ 1,342°, ширина суммарной ДН 00,5 ≈ 0,855°.
Характеристики антенной системы в программной реализации математической модели предлагаемого способа идентичны характеристикам антенной системы РЛС.
Вычисляется горизонтальная дальность RГ.
RГ=19970 м.
Вычисляется значение косинуса суммарного угла отклонения луча от нормали θХ:
cos θХ ≈ 0,8704.
Вычисляется угол положения центра луча радиолокатора εЛ:
εЛ=0,506°.
Вычисляются значения амплитуд в относительных единицах в суммарном канале, угломестном и азимутальном разностных каналах:
АΣ=22,41; АЕ=1,286; Ав=0,238.
Вычисляется величина необходимой расстройки по азимуту B1 в градусах:
B1=0,007162°.
Исходя из значений полученных амплитуд, вычисляется контрольное значение разности фаз между суммами квадрантов полотна (А+В) и (С+D) (9) в градусах:
Δ_ϕABCD≈-6,104°.
Затем во всем угловом диапазоне углов места ε выполняется поиск глобального минимума функции модуля F_min_kv(ε) (18). При этом вычисляются векторы прямых сигналов a1B, a1B, a1C, a1D (12), векторы сигналов «антипода» а2A, а2B, а2C, а2D (13÷14), фазы векторов суммарного канала Arg_Sum и угломестного разностного канала Arg_E (17). Коэффициент отражения К2 вычисляется по формуле (15).
В результате поиска глобального минимума функции модуля F_min_kv (ε) вычисляется ряд минимумов (см. фиг. 4).
Наименьшее значение минимума функции модуля (18) (глобальный минимум) равно F_min_kv (ε) ≈ 0,03° и соответствует углу места ε ≈ 0,554 ÷ 0,5545° (см. фиг. 5). Из этого делаем вывод, что найден истинный угол места εИСТ ≈ 0,554 ÷ 0,5545°. Минимумы модулей ложных углов превышают это значение в несколько раз (см. фиг. 4).
Надо отметить, что исходные данные должны поступать на вход программы вычисления высоты полета НЛЦ с пренебрежимо малыми ошибками, в этом случае глобальный минимум функции модуля (18) будет практически равен нулю.
Глобальный минимум функции модуля (18) для истинного угла места εИСТ имеет острый, ярковыраженный характер (см. фиг. 5), что позволяет уточнить значение истинного угла места НЛЦ εИСТ=0,55438°. Для полученного истинного угла места εИСТ вычисленный коэффициент отражения К2 (15) составляет К2 ≈ 0,0477. Высота полета мишени вычисляется по формуле (19):
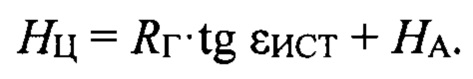
Таким образом, высота полета НЛЦ составляет HЦ ≈ 198,73 м.
Предлагаемый способ позволяет по результатам одного зондирования РЛС, то есть в реальном масштабе времени, определять истинный угол места НЛЦ εИСТ и высоту ее полета НЦ.
Предлагаемый способ основан на однозначном соответствии истинному углу места НЛЦ εИСТ данных, получаемых от РЛС на данном такте зондирования: координат НЛЦ X, Y, Z, амплитуд сигналов в суммарном канале AΣ, угломестном АЕ и азимутальном АВ разностных каналах, контрольного значения фазы сигнала в суммарном канале Ф_Sum, контрольного значения фазы сигнала в угломестном разностном канале Ф_Е, значений синусов углов отклонения луча РЛС ϕВ и ϕН в угломестной и в наклонной плоскостях: sin ϕВ и sin ϕН. Угол β «антипода», сдвиг по фазе δ между прямым сигналом и сигналом «антипода» и коэффициент отражения от подстилающей поверхности К2 определяются как функции одной переменной - угла места ε. В процессе проводимого одномерного поиска по углу места ε путем сравнения вычисляемых значений фазы вектора суммарного канала Arg_Sum и фазы вектора угломестного разностного канала Arg_E с контрольными значениями фазы сигнала в суммарном канале и фазы сигнала в угломестном разностном канале определяется и уточняется значение истинного угла места НЛЦ εИСТ и вычисляется высота полета НЛЦ НЦ.
Предложенный способ не требует знания номера «колокола» сигнала СС по углу места с момента выхода НЛЦ из-за радиогоризонта, то есть не нужна информация о количестве набегов разности фаз в 180° между прямым сигналом и сигналом «антипода».
Заявляемый способ позволяет определять угол места НЛЦ и высоту ее полета в любой момент сопровождения НЛЦ.
В предлагаемом способе точность определения высоты полета НЛЦ практически определяется точностью определения дальности до цели R, которая поступает от РЛС при сопровождении, точностью поступающих значений синусов углов отклонения луча РЛС в угломестной и в наклонной плоскостях sin ϕВ и sin ϕН, точностью поступающих контрольных значений фазы сигнала в суммарном канале Ф_Sum и фазы сигнала в угломестном канале Ф_Е, точностью поступающих значений амплитуд сигналов в суммарном канале AΣ, угломестном АЕ и азимутальном АВ разностных каналах.
В предлагаемом способе при вычислении высоты полета НЛЦ контур сопровождения СС по углу места не разрывается.
В заявляемом способе не требуется проведение каких-либо конструктивных или аппаратурных изменений в РЛС, введения дополнительной квадратурной обработки, изменения высоты антенны РЛС.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ высокоточного определения высоты полета низколетящей цели моноимпульсной РЛС сопровождения | 2021 |
|
RU2779039C1 |
| Способ определения высоты полета низколетающей цели моноимпульсной РЛС сопровождения | 2021 |
|
RU2761955C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТРАЕКТОРИИ ДВИЖЕНИЯ НИЗКОЛЕТЯЩИХ ЦЕЛЕЙ | 2017 |
|
RU2667484C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛА МЕСТА И ДАЛЬНОСТИ НИЗКОЛЕТЯЩЕЙ ЦЕЛИ МОНОИМПУЛЬСНЫМ РАДИОЛОКАТОРОМ ПРИ МНОГОЛУЧЕВОМ РАСПРОСТРАНЕНИИ ОТРАЖЕННОГО ОТ ЦЕЛИ СИГНАЛА | 1994 |
|
RU2080619C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛА МЕСТА НИЗКОЛЕТЯЩЕЙ ЦЕЛИ И МОНОИМПУЛЬСНАЯ РЛС ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2023 |
|
RU2802886C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОМЕСТНОЙ КООРДИНАТЫ НИЗКОЛЕТЯЩЕЙ ЦЕЛИ | 2010 |
|
RU2444750C2 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛА МЕСТА НИЗКОЛЕТЯЩЕЙ ЦЕЛИ И РАДИОЛОКАЦИОННАЯ СТАНЦИЯ ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2307375C1 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛА МЕСТА ЦЕЛЕЙ ПРИ НАЛИЧИИ ОТРАЖЕНИЙ ПРИНИМАЕМОГО ЭХОСИГНАЛА ОТ ЗЕМНОЙ ПОВЕРХНОСТИ И ИМПУЛЬСНАЯ НАЗЕМНАЯ ТРЕХКООРДИНАТНАЯ РАДИОЛОКАЦИОННАЯ СТАНЦИЯ ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2005 |
|
RU2291464C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОШИБКИ ИЗМЕРЕНИЯ СКОРОСТИ ЛА ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМОЙ И БОРТОВОЙ НАВИГАЦИОННЫЙ КОМПЛЕКС ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2008 |
|
RU2411538C2 |
| РАДИОЛОКАЦИОННАЯ СТАНЦИЯ С ПЕРЕСТРОЙКОЙ ЧАСТОТЫ, ИНВЕРСНЫМ СИНТЕЗИРОВАНИЕМ АПЕРТУРЫ И ДВУХУРОВНЕВЫМ НЕЙРОСЕТЕВЫМ РАСПОЗНАВАНИЕМ ОБЪЕКТОВ ПО СОВОКУПНОСТИ ПРИЗНАКОВ | 2009 |
|
RU2412451C1 |
Изобретение относится к радиолокации и может быть использовано в радиолокационной станции (РЛС) сопровождения низколетящих целей (НЛЦ) под малыми углами места при наличии мешающих отражений от подстилающей поверхности. Техническим результатом является повышение точности определения высоты полета НЛЦ при одновременном упрощении конструкции антенной системы РЛС. Способ определения высоты полета НЛЦ моноимпульсной РЛС сопровождения в реальном масштабе времени характеризуется формированием и излучением зондирующих радиолокационных сигналов, приемом отраженных эхо-сигналов от НЛЦ и от подстилающей поверхности и их обработкой с помощью ЭВМ РЛС для определения дальности до НЛЦ, определения высоты ее полета и соответствующего взаимного геометрического расположения РЛС и НЛЦ. В РЛС используется антенна с 4-мя квадрантами А, В, С, D полотна, реализующими суммарно-разностную обработку по углу места и в наклонной плоскости. Способ основан на вычислении угла «антипода», разности фаз между прямым сигналом и сигналом «антипода» и коэффициента отражения от подстилающей поверхности как функций одной переменной угла места. Это дает возможность при использовании данных сопровождения НЛЦ, поступающих с приемного устройства РЛС на данном такте зондирования, и значений параметров антенной системы РЛС вычислять значения векторов прямого сигнала и сигнала «антипода» и определять значения фазы вектора суммарного канала и фазы вектора угломестного разностного канала. В процессе проводимого одномерного поиска по углу места путем сравнения вычисляемых значений фаз с контрольным значением фазы сигнала в суммарном канале и с контрольным значением фазы сигнала в угломестном разностном канале определяются истинный угол места НЛЦ и высота ее полета. 5 ил.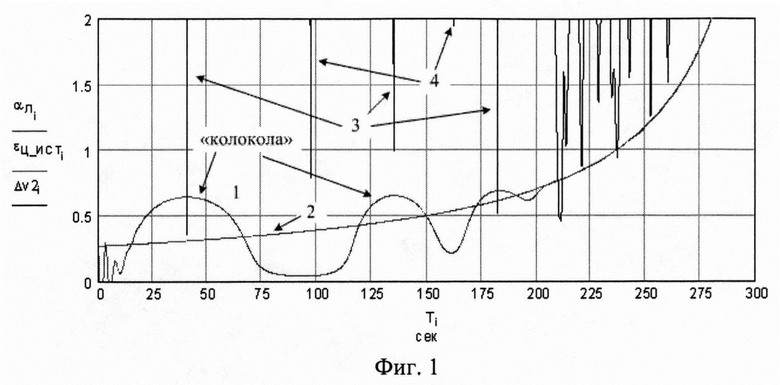
Способ определения высоты полета низколетящей цели (НЛЦ) моноимпульсной РЛС сопровождения в реальном масштабе времени, характеризующийся формированием и излучением зондирующих радиолокационных сигналов, приемом отраженных эхо-сигналов от НЛЦ и от подстилающей поверхности и их обработкой с помощью ЭВМ РЛС для определения дальности до НЛЦ, определения высоты ее полета и соответствующего взаимного геометрического расположения РЛС и НЛЦ, отличающийся тем, что в РЛС используется антенна с 4-мя квадрантами А, В, С, D полотна, реализующими суммарно-разностную обработку по углу места и в наклонной плоскости, при этом выполняется вычисление угла сигнала, отраженного от подстилающей поверхности, разности фаз между прямым сигналом и сигналом, отраженным от подстилающей поверхности, и коэффициента отражения от подстилающей поверхности как функций угла места НЛЦ, что при использовании исходных данных сопровождения НЛЦ, поступающих с приемного устройства РЛС на программу ЭВМ РЛС вычисления высоты НЛЦ на каждом такте зондирования: текущих координат НЛЦ X, Y, Z, значений амплитуд сигналов в суммарном канале АΣ, угломестном АΕ и азимутальном АΒ разностных каналах, значений синусов углов отклонения луча РЛС ϕв и ϕн в угломестной и наклонной плоскостях 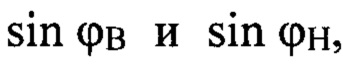 контрольного значения фазы сигнала в суммарном канале
контрольного значения фазы сигнала в суммарном канале 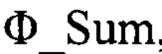 , контрольного значения фазы сигнала в угломестном разностном канале
, контрольного значения фазы сигнала в угломестном разностном канале 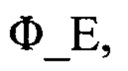 длины рабочей волны РЛС λ метрового, дециметрового или сантиметрового диапазона и значений параметров антенной системы РЛС: угла отклонения нормали к полотну антенны от горизонтали εΑ, значений баз антенны РЛС
длины рабочей волны РЛС λ метрового, дециметрового или сантиметрового диапазона и значений параметров антенной системы РЛС: угла отклонения нормали к полотну антенны от горизонтали εΑ, значений баз антенны РЛС 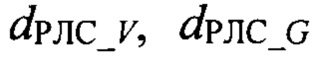 для угломестного и азимутального разностных каналов с учетом фактического уменьшения базы антенны РЛС в угломестной плоскости из-за угла отклонения луча РЛС в угломестной плоскости от нормали к полотну антенны ϕв, значения высоты фазового центра антенны РЛС НA, позволяет вычислить значения векторов прямого сигнала a1A, a1B, a1C, a1D и сигнала, отраженного от подстилающей поверхности, a2A, a2B, a2C, a2D в квадрантах А, В, С, D и определить значения фазы вектора суммарного канала
для угломестного и азимутального разностных каналов с учетом фактического уменьшения базы антенны РЛС в угломестной плоскости из-за угла отклонения луча РЛС в угломестной плоскости от нормали к полотну антенны ϕв, значения высоты фазового центра антенны РЛС НA, позволяет вычислить значения векторов прямого сигнала a1A, a1B, a1C, a1D и сигнала, отраженного от подстилающей поверхности, a2A, a2B, a2C, a2D в квадрантах А, В, С, D и определить значения фазы вектора суммарного канала 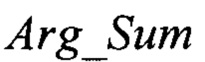 и фазы вектора угломестного разностного канала
и фазы вектора угломестного разностного канала 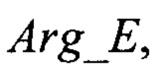 затем в процессе проводимого одномерного поиска по углу места ε путем сравнения вычисляемых значений фаз
затем в процессе проводимого одномерного поиска по углу места ε путем сравнения вычисляемых значений фаз 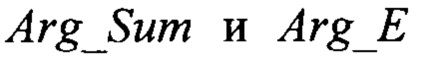 с контрольным значением фазы сигнала в суммарном канале
с контрольным значением фазы сигнала в суммарном канале 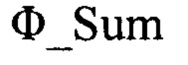 и с контрольным значением фазы сигнала в угломестном разностном канале
и с контрольным значением фазы сигнала в угломестном разностном канале 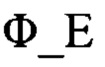 определяются истинный угол места НЛЦ и высота ее полета, при этом способ осуществляется в 2 последовательных этапа: на 1-м этапе после развертывания РЛС в точке ее дислокации в память ЭВМ РЛС вводятся точные координаты места дислокации РЛС, в том числе по высоте относительно уровня моря, точное время системы единого времени (СЕВ) с помощью входящего в РЛС спутникового навигатора с атомными часами, на 2-м этапе с помощью РЛС осуществляют сопровождение НЛЦ, при этом в реальном масштабе времени на каждом такте зондирования РЛС вычисляется значение горизонтальной дальности Rr НЛЦ:
определяются истинный угол места НЛЦ и высота ее полета, при этом способ осуществляется в 2 последовательных этапа: на 1-м этапе после развертывания РЛС в точке ее дислокации в память ЭВМ РЛС вводятся точные координаты места дислокации РЛС, в том числе по высоте относительно уровня моря, точное время системы единого времени (СЕВ) с помощью входящего в РЛС спутникового навигатора с атомными часами, на 2-м этапе с помощью РЛС осуществляют сопровождение НЛЦ, при этом в реальном масштабе времени на каждом такте зондирования РЛС вычисляется значение горизонтальной дальности Rr НЛЦ:
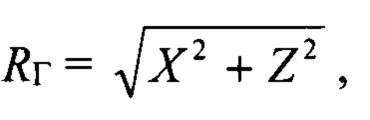
затем вычисляется косинус суммарного угла отклонения луча РЛС θx от нормали к антенному полотну:
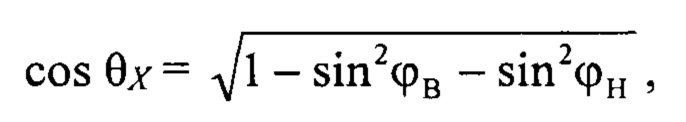
после этого вычисляется угол положения центра луча радиолокатора:
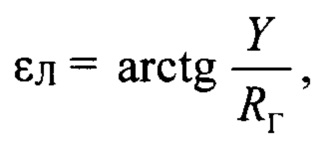
далее вычисляется отношение амплитуд сигналов в суммарном и азимутальном разностном каналах КΣ_Β
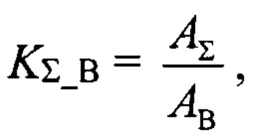
затем вычисляется необходимая расстройка по азимуту B1:
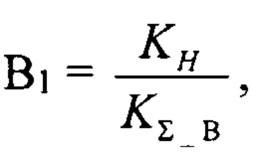
где КН - нормирующий коэффициент в приемном устройстве РЛС, после этого вычисляется значение сигнала в угломестном разностном канале:
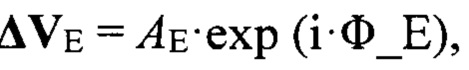
где i - мнимая единица,
далее вычисляются значения сигналов в суммах квадрантов (А+В) и (С+D) SumAB и SumCD:
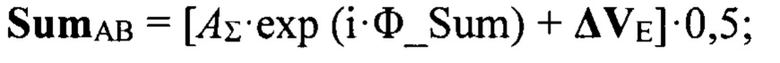
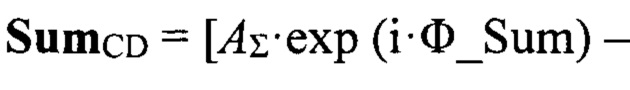
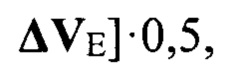
после этого вычисляется контрольное значение разности фаз Δ_ϕABCD между суммами квадрантов полотна (А+В) и (С+D):

где Arg(…) - функция вычисления аргумента комплексной величины, после этого используется формула для вычисления угла сигнала, отраженного от подстилающей поверхности, β для «плоской» Земли как функции угла места цели ε:
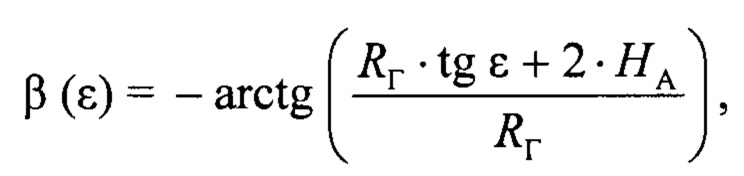
где НA - высота фазового центра антенны РЛС, затем используется формула для вычисления сдвига по фазе δ между прямым сигналом и сигналом, отраженным от подстилающей поверхности, как функции угла места цели ε:
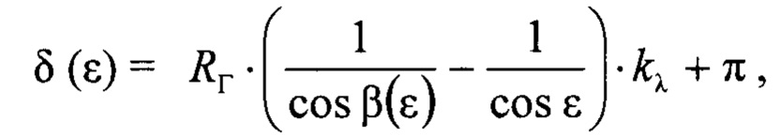
где kλ=2⋅π/λ - модуль волнового вектора;
π - дополнительный сдвиг фазы при отражении, после этого используются формулы для вычисления прямых сигналов от НЛЦ в квадрантах полотна антенны А, В, С, D:
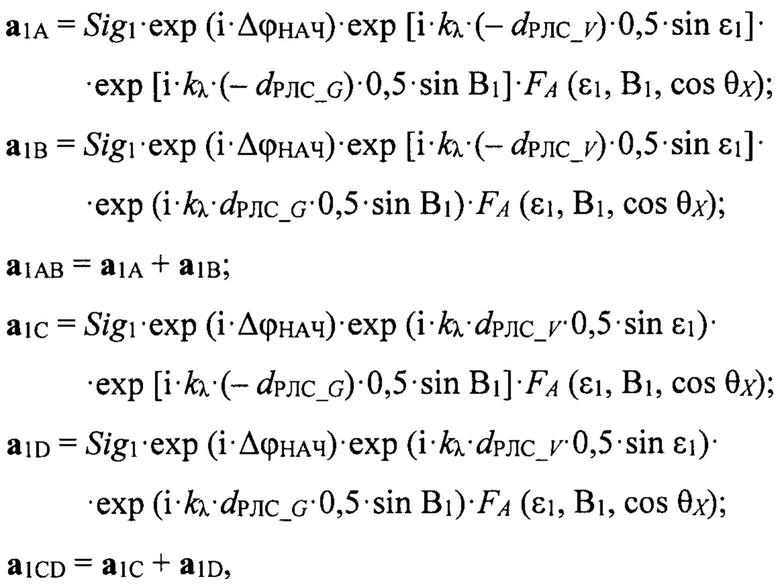
где Sig1=1 - амплитуда прямого сигнала от цели;
угол ε1=ε-εЛ;
FA (ε1,B1,cos θx) - функция ДН одного квадранта антенны РЛС, главный лепесток которой аппроксимируется функцией вида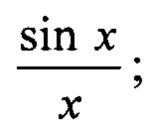
i - мнимая единица;
ΔϕНАЧ=0 - начальная фаза сигнала, далее используются формулы для вычисления сигналов, отраженных от подстилающей поверхности, в квадрантах полотна антенны А, В, С, D:
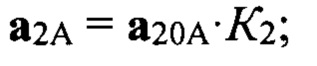
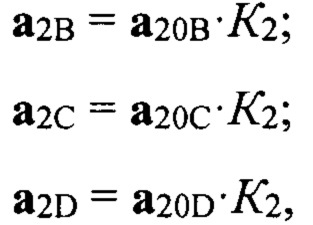
где К2 - коэффициент отражения от подстилающей поверхности, который реализовался на данном такте зондирования, причем для вычисления сигналов а20А, а20В, а20С a20D используются формулы:
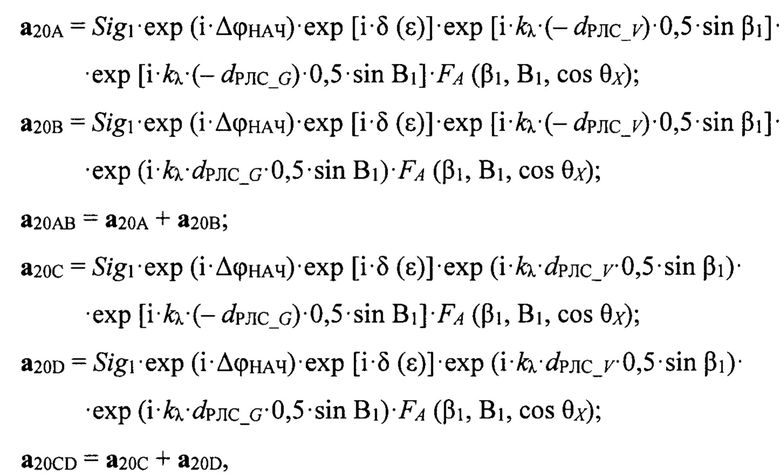
где δ(ε) - сдвиг по фазе между прямым сигналом и сигналом, отраженным от подстилающей поверхности;
угол β1=β-εЛ;
i - мнимая единица;
FA (β1,B1,cosθx) - функция ДН одного квадранта антенны РЛС, главный лепесток которой аппроксимируется функцией вида 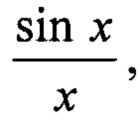 после этого используется квадратное уравнение для вычисления коэффициента отражения К2.
после этого используется квадратное уравнение для вычисления коэффициента отражения К2.
А⋅К2+K⋅B+С=0, при этом используются формулы для вычисления коэффициентов А, В, C

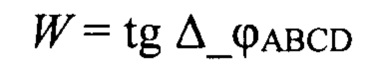 - тангенс контрольного значения разности фаз
- тангенс контрольного значения разности фаз 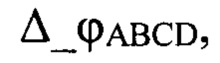 при этом коэффициент К2=-1, если величина В2-4А⋅С<0, причем неверный корень квадратного уравнения отбрасывается из условия, что коэффициент отражения К2 может быть только положительным и меньшим единицы, то есть используются формулы для вычисления угла β сигнала, отраженного от подстилающей поверхности, сдвига по фазе δ между прямым сигналом и сигналом, отраженным от подстилающей поверхности, и коэффициента отражения от подстилающей поверхности К2 в виде функций угла места цели ε, затем вычисляется фаза вектора суммарного канала
при этом коэффициент К2=-1, если величина В2-4А⋅С<0, причем неверный корень квадратного уравнения отбрасывается из условия, что коэффициент отражения К2 может быть только положительным и меньшим единицы, то есть используются формулы для вычисления угла β сигнала, отраженного от подстилающей поверхности, сдвига по фазе δ между прямым сигналом и сигналом, отраженным от подстилающей поверхности, и коэффициента отражения от подстилающей поверхности К2 в виде функций угла места цели ε, затем вычисляется фаза вектора суммарного канала 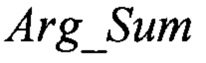 и фаза вектора угломестного разностного канала
и фаза вектора угломестного разностного канала 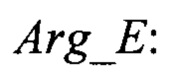

после этого для селекции ложных углов места и определения истинного угла места НЛЦ во всем угловом диапазоне углов места ε, начиная с нулевого значения и до значения ширины суммарной ДН антенны РЛС по уровню 0,5, выполняется одномерный поиск глобального минимума модуля фазы вектора суммарного канала 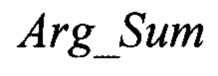 относительно контрольного значения фазы
относительно контрольного значения фазы 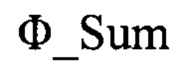 и фазы вектора угломестного разностного канала
и фазы вектора угломестного разностного канала 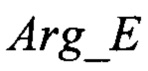 относительно контрольного значения фазы Ф_Е, причем для этого используется формула для вычисления функции модуля:
относительно контрольного значения фазы Ф_Е, причем для этого используется формула для вычисления функции модуля:
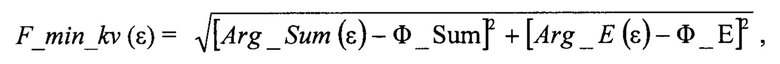
при этом глобальный минимум функции 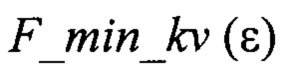 определяет значение истинного угла места НЛЦ εИСТ и высоту полета НЛЦ НЦ:
определяет значение истинного угла места НЛЦ εИСТ и высоту полета НЛЦ НЦ:
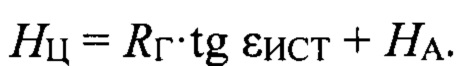
Авторы
Даты
2024-03-26—Публикация
2023-04-25—Подача