Изобретение относится к радиолокации и может быть использовано в радиолокационной станции (РЛС) сопровождения низколетящих целей под малыми углами места при наличии мешающих отражений от подстилающей поверхности.
В практической работе современных РЛС одной из важнейших задач является обнаружение и сопровождение низколетящих целей (НЛЦ). При сопровождении НЛЦ важно как можно раньше правильно определить ее угломестную координату (оценить высоту ее полета), чему мешают значительные угломестные ошибки из-за многопутного распространения (явления многолучевости), иначе говоря, из-за сигнала так называемого «антипода» - сигнала, отраженного от подстилающей поверхности.
В результате появления сигнала «антипода» в угломестном разностном канале появляется ложный сигнал ошибки, из-за чего следящая система (СС) по углу места сдвигает луч антенны РЛС до тех пор, пока этот ложный сигнал не будет скомпенсирован. При сопровождении на малых углах места ошибка из-за многопутного распространения очень велика, так как сигнал «антипода» попадает в главный лепесток диаграммы направленности (ДН) антенны РЛС. При этом реальная НЛЦ и сигнал «антипода» образуют двухточечную цель с изменяющейся разностью фаз и амплитудами сигналов, которые сравнимы по величине. Под воздействием сигнала ошибки СС луч антенны РЛС периодически то устремляется к нулевому углу места, то, при достижении сдвига фаз между сигналами в 180°, снова движется вверх по направлению к НЛЦ [«Справочник по радиолокационным измерениям». Д. Бартон, Г. Вард. Москва, «Советское радио», 1976 г.]. При этом сигнал СС образует локальные максимумы, так называемые «колокола».
Известны следующие способы определения высоты полета НЛЦ [А.И. Леонов, К.И. Фомичев. «Моноимпульсная радиолокация». Москва, «Радио и связь», 1984 г.].
Для борьбы с явлением многопутного распространения при сопровождении НЛЦ используются различные методы, которые можно условно разделить на две группы.
К первой относятся методы, направленные на создание узконаправленных по углу места ДН антенн с целью уменьшения (или исключения) проникновения сигнала «антипода» в главный луч ДН антенны. Практическая реализация этих способов подразумевает увеличение апертуры антенной системы по вертикали и по горизонтали. Повышение угловой разрешающей способности лежит в основе этих способов. Реализация крупногабаритных антенн затруднительна для большинства передвижных радиолокаторов, предназначенных для обнаружения и сопровождения НЛЦ, так как повышается конструктивно-технологическая сложность систем и снижается их мобильность.
Вторая группа способов определения угла места (высоты НЛЦ) основана на использовании дополнительной информации о влиянии отражений от подстилающей поверхности и устранении или уменьшении этого влияния на оценку угла места (высоты) НЛЦ. К этому подклассу относится большое число методов, основанных на моноимпульсном методе измерения угломестной координаты. Моноимпульсные способы измерения угла места НЛЦ имеют преимущества, как наиболее устойчивые к шумовым и динамическим ошибкам измерения.
В работе [А.И. Леонов, К.И. Фомичев. «Моноимпульсная радиолокация». Москва, «Радио и связь», 1984 г.] описан способ определения угла места НЛЦ, при котором используются две антенны в вертикальной плоскости, расположенные на разной высоте. Антенны имеют идентичные ДН и одинаковую ориентацию по углу места. Расстояние между антеннами регулируется так, чтобы разность фаз между сигналами от «антипода», принимаемых двумя антеннами, равнялась ж. При этом разность фаз между сигналами от НЛЦ должна быть отлична от п. В зависимости от амплитуды и фазы сигналов (от НЛЦ и «антипода»), принятых антеннами, вырабатываются сигналы управления сдвигом фазы сигнала (от НЛЦ и антипода) и разнесением антенн по высоте. Если сигнал ошибки от НЛЦ и управляющий сигнал разнесения антенн одновременно равняются нулю, то система отслеживает направление на НЛЦ со сравнительно малыми ошибками. Указанный способ, несмотря на высокую точность определения угла места НЛЦ, весьма сложен в конструктивном отношении, требует использования дополнительной антенны.
Наиболее близким по технической сущности к заявляемому способу является способ вычисления высоты полета НЛЦ, описанный в [патент RU №2080619 C1, МПК G01S 13/44. Способ определения угла места и дальности низколетящей цели моноимпульсным радиолокатором при многолучевом распространении отраженного от цели сигнала. 1994 г.], характеризующийся формированием и излучением зондирующих радиолокационных сигналов, приемом отраженных эхо-сигналов от НЛЦ и от подстилающей поверхности (сигнала «антипода») и их обработкой с помощью ЭВМ РЛС для определения угла места НЛЦ без размыкания контура СС по углу места.
Недостатком прототипа является то, что этот способ работает тогда, когда известно, что рассматривается 1-ый нуль мнимой функции (Im), то есть набег фаз в 180° между прямым сигналом от НЛЦ и сигналом «антипода» произошел только один раз. Для последующих нулей мнимой функции (Im) этот способ работать не будет из-за неоднозначности вычислений. Кроме того, для реализации этого способа необходимо организовывать дополнительную квадратурную обработку принимаемого сигнала в угломестном канале, и возникает необходимость изменения высоты антенны РЛС.
Недостатком прототипа также является отсутствие привязки РЛС по координатам и по высоте относительно уровня моря и к системе единого времени (СЕВ).
Особенностью заявляемого способа является то, что в нем не снижается отрицательное влияние явления многолучевости на характер сигнала СС, а, наоборот, используются вышеописанные локальные максимумы сигнала СС («колокола»), вызванные проникновением сигнала «антипода» в главный луч ДН антенны, и, кроме того, используется сигнал ошибки Δγ дополнительного диагонального разностного канала. Предлагаемый способ не требует изменения высоты антенны РЛС и основан на анализе изменения разности хода (и разности фаз) между прямым сигналом и сигналом «антипода» при движении НЛЦ.
Техническим результатом изобретения является устранение недостатков прототипа - более точное определение высоты полета НЛЦ при одновременном упрощении конструкции антенной системы РЛС, путем учета при определении высоты НЛЦ расширенных данных, влияющих на ее точность, полученных до начала развертывания РЛС в точке дислокации (точные координаты, в том числе высота РЛС относительно уровня моря) и при радиолокационном сопровождении НЛЦ в реальном масштабе единого времени (отраженных радиолокационных сигналов от НЛЦ и от подстилающей поверхности) при учете фазовых соотношений между прямым сигналом и сигналом «антипода», позволяющие более точно измерять дальность до НЛЦ и, как следствие, ее высоту.
Кроме того, в заявляемом способе не требуется проведение каких-либо конструктивных или аппаратурных изменений в РЛС, введения дополнительной квадратурной обработки, изменения высоты антенны РЛС и т.д.
В заявляемом способе точность определения высоты полета НЛЦ в основном определяется точностью определения дальности R, соответствующей центру анализируемого «колокола», которая поступает от РЛС при сопровождении НЛЦ.
Указанный технический результат достигается тем, что используется способ высокоточного определения высоты полета НЛЦ моноимпульсной РЛС сопровождения, характеризующийся формированием и излучением зондирующих радиолокационных сигналов, приемом отраженных эхо-сигналов от НЛЦ и от подстилающей поверхности и их обработкой с помощью ЭВМ РЛС для определения дальности до НЛЦ, определения высоты ее полета и соответствующего взаимного геометрического расположения РЛС и НЛЦ. Особенностью этого способа является то, что в РЛС используется антенна с 4-мя квадрантами А, В, С, D полотна, реализующими суммарно-разностную обработку по углу места и в наклонной плоскости. При этом для повышения точности определения высоты полета НЛЦ используется дополнительный диагональный разностный канал, который образуется согласно логике (SigA+SigD) - (SigB+SigC), где SigA, SigB, SigD, SigC - сигналы с квадрантов А, В, D, С, причем для получения ненулевого сигнала ошибки Δγ с этого дополнительного диагонального разностного канала при сопровождении НЛЦ в наклонной плоскости выполняется расстройка в наклонной плоскости в βр градусов:
βр=(0,4÷0,6)⋅θ0,5,
где θ0,5 - ширина суммарной ДН антенны РЛС.
Способ осуществляется в 3 последовательных этапа:
на 1-м этапе после развертывания РЛС в точке ее дислокации в память ЭВМ РЛС вводятся точные координаты дислокации РЛС, в том числе, по высоте относительно уровня моря, точное время системы единого времени (СЕВ) с помощью входящего в РЛС спутникового навигатора с атомными часами,
на 2-м этапе с помощью РЛС осуществляют сопровождение НЛЦ, при этом на каждом такте работы РЛС в ЭВМ РЛС запоминаются значения сигнала СС по углу места 8 л, то есть потактно формируется числовой массив. В ЭВМ РЛС потактно анализируется величина сигнала εЛ и при монотонном увеличении величины сигнала СС εЛ, что является признаком начала очередного локального максимума сигнала СС по углу места, на каждом такте работы РЛС в ЭВМ РЛС запоминаются значения модуля сигнала угломестного разностного канала Δv и значения сигнала ошибки Δγ дополнительного диагонального разностного канала, для чего вход приемного канала РЛС по азимуту периодически переключается на выход этого диагонального разностного канала с антенной системы РЛС с частотой, меньшей, чем основная частота зондирования РЛС. При этом потактно формируются дополнительно еще 2 числовых массива, затем фиксируется момент времени Т2 прохождения сигнала ошибки Δγ диагонального разностного канала через ноль, которому также соответствует момент наступления минимума модуля сигнала угломестного разностного канала Δv, запоминается значение дальности R2 от РЛС до НЛЦ, определяемое РЛС в этот момент Т2 запоминается значение скорости НЛЦ VЦ, определяемое РЛС. Затем в полученном массиве сигнала ошибки Δγ диагонального разностного канала определяется максимум и соответствующий ему момент времени Т1, также в момент времени Т1 определяется дальность от РЛС до НЛЦ R1,
на 3-м этапе на интервале от момента Т1 до момента Т2 определяются сумма сигнала ошибки Δγ диагонального разностного канала SuntΔγ в градусах и сумма сигнала СС εЛ по углу места SumTS в градусах, и затем высота полета НЛЦ определяется из целевой функции:
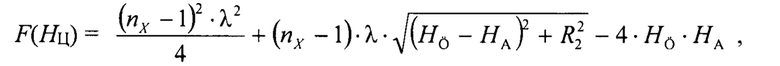
где nx - натуральное число, большее или равное 2 (n=2, 3, 4, 5, …), которое равно неизвестному количеству набегов разности фаз в 180° между прямым сигналом и сигналом, отраженным от подстилающей поверхности;
HA - высота фазового центра антенны РЛС;
НЦ - высота полета НЛЦ;
λ - длина рабочей волны РЛС метрового, дециметрового или сантиметрового диапазона;
R2 - дальность от РЛС до НЛЦ, соответствующая центру анализируемого локального максимума сигнала СС εЛ по углу места, и определяемая РЛС в момент Т2 минимума модуля сигнала угломестного разностного канала Δv. Затем с помощью одномерного поиска нуля целевой функции F(НЦ) по переменной НЦ определяется ряд возможных высот полета НЛЦ НЦ, каждая из которых соответствует одному из значений переменной nx. После этого для определения истинной высоты полета НЛЦ для каждого полученного значения высоты НЦ запускается программа ЭВМ РЛС движения НЛЦ с тем же значением такта зондирования, со скоростью НЛЦ VЦ и с дальности R1, соответствующей моменту Т1, до дальности R2, соответствующей моменту Т2. В этой программе ЭВМ РЛС используются характеристики антенной системы РЛС, выполняется замыкание обоих СС по углу места и в наклонной плоскости. Эта программа потактно определяет взаимное геометрическое расположение РЛС и НЛЦ, движущейся со скоростью VЦ на высоте НЦ, потактно определяет разность хода и разность фаз прямого луча и сигнала, отраженного от подстилающей поверхности, и вырабатывает сигнал ошибки Δγ диагонального разностного канала и сигнал СС по углу места εЛ с теми же значениями тактов, которые были использованы при работе РЛС. При работе этой программы для каждого полученного с помощью функции F(НЦ) значения высоты НЦ с момента Т1 до момента Т2 определяются значения сумм сигнала ошибки Δγ диагонального разностного канала в градусах и сигнала СС по углу места εЛ в градусах ∑Δγ и ∑ εЛ, работа указанной программы прекращается тогда, когда полученное значение суммы ∑Δγ становится более чем в 4÷5 раз меньше величины SumΔγ. Затем для значений высоты НЦ, которым соответствуют значения полученных сумм Е ел, не меньшие половины величины SumTS, значения суммы ∑Δγ, являющиеся результатом работы этой программы, сравниваются с суммой сигнала ошибки Δγ диагонального разностного канала SumΔy, которое было получено при работе РЛС. В результате этого определяется ближайшее значение Е Δγ к величине SumΔγ, что определяет истинное значение высоты полета НЛЦ НЦ. При этом выполняется регулярное определение высоты полета НЛЦ на каждом очередном локальном максимуме сигнала СС по углу места, и получаемая оценка высоты постоянно уточняется на всем интервале сопровождения НЛЦ.
На фиг. 1, 2, 3, …, 6 соответственно представлены:
фиг. 1 - характерный вид локальных максимумов сигнала СС по углу места («колокола» сигнала СС по углу места), истинный угол места НЛЦ, минимумы модуля сигнала угломестного разностного канала;
фиг. 2 - геометрия распространения прямого луча и луча, отраженного от Земли для «плоской» Земли;
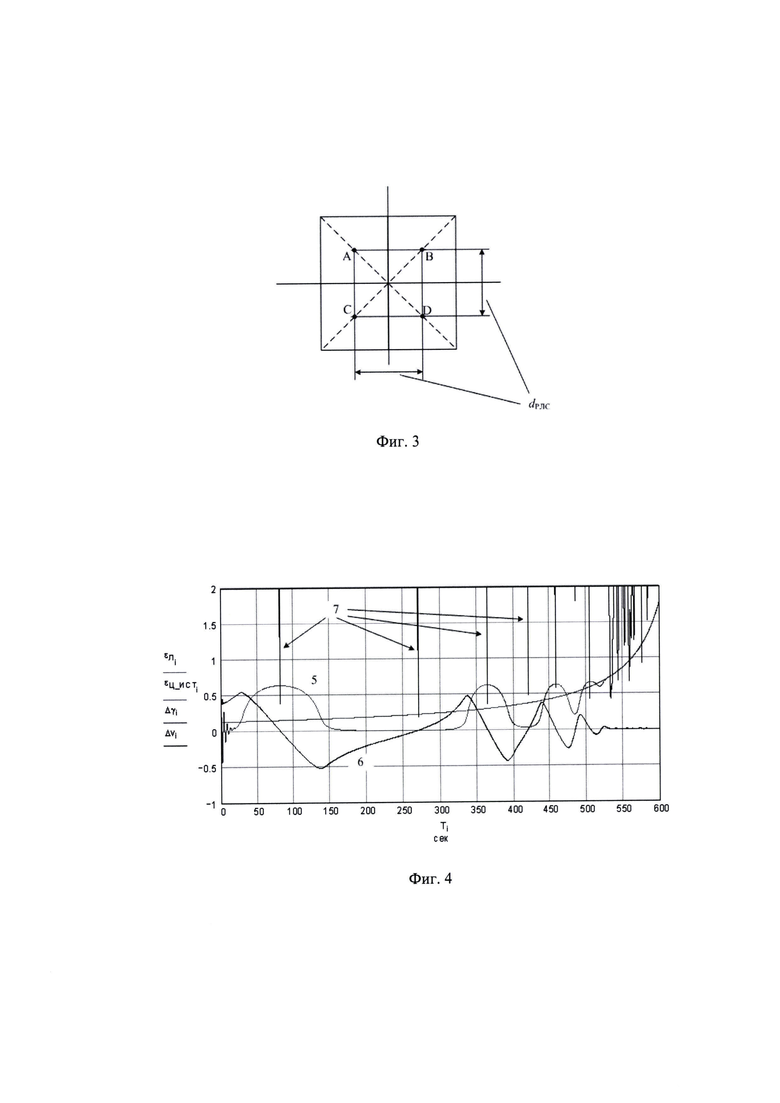
фиг. 3 - классический вид квадратного полотна антенны моноимпульсной РЛС;
фиг. 4 - сигнал СС по углу места («колокола» сигнала СС по углу места), сигнал ошибки диагонального разностного канала, минимумы модуля сигнала угломестного разностного канала;
фиг. 5 - кривая изменения коэффициента зеркального отражения pi в зависимости от времени наблюдения НЛЦ;
фиг. 6 - кривые сигнала ошибки диагонального разностного канала при различных значениях высоты полета НЛЦ для 1-го «колокола» сигнала СС (см. фиг. 4).
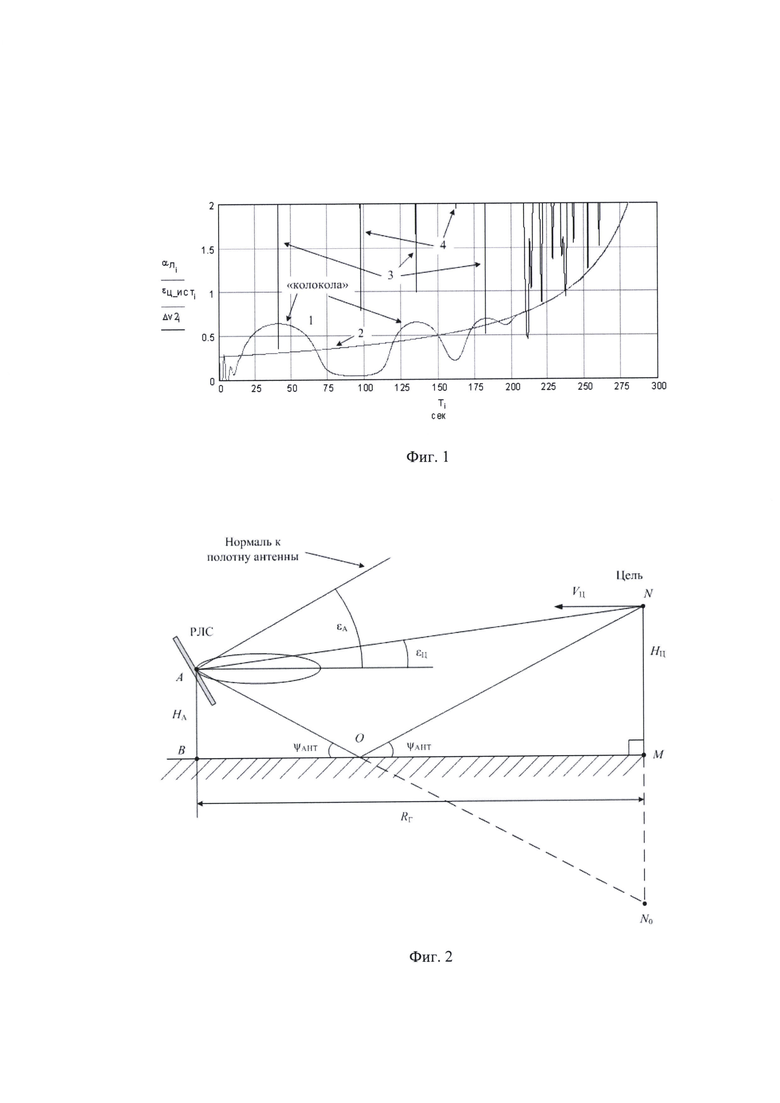
На фиг. 1 обозначено: кривая 1 - сигнал СС по углу места в градусах; кривая 2 - изменение истинного угла места НЛЦ в градусах; кривые 3 - минимумы модуля сигнала в угломестном разностном канале, соответствующие центрам «колоколов» и разности фаз между сигналами в 180°; кривые 4 -минимумы модуля сигнала в угломестном разностном канале, соответствующие разности фаз между сигналами в 0°. По оси абсцисс отложено время в секундах. По оси ординат отложены градусы.
На фиг. 2 обозначено: HA - высота фазового центра антенны РЛС; εA - угол поднятия нормали к полотну антенны РЛС относительно горизонта; εЦ - истинный угол места НЛЦ; НЦ - высота полета НЛЦ; VЦ - скорость полета НЛЦ; ψAHT - угол скольжения сигнала «антипода»; RГ - горизонтальная дальность до НЛЦ; А - положение фазового центра антенны РЛС; О - точка отражения сигнала «антипода»; N - положение НЛЦ; N0 - зеркальное положение НЛЦ.
На фиг. 3 обозначено: А, В, С, D - квадранты полотна антенны моноимпульсной РЛС; dРЛС - база антенны РЛС.
На фиг. 4 обозначено: кривая 5 - сигнал СС по углу места («колокола» сигнала СС по углу места); кривая 6 - сигнал ошибки диагонального разностного канала; кривые 7 -минимумы модуля сигнала угломестного разностного канала.
На фиг. 5 по оси абсцисс отложено время в секундах. Ось ординат безразмерная.
На фиг. 6 обозначено: кривая 8 - сигнал ошибки диагонального разностного канала при высоте полета НЛЦ НЦ=100 м, кривая 9 -сигнал ошибки диагонального разностного канала при высоте полета НЛЦ НЦ=200 м, кривая 10 -сигнал ошибки диагонального разностного канала при высоте полета НЛЦ НЦ=300 м, кривая 11 - сигнал ошибки диагонального разностного канала при высоте полета НЛЦ НЦ=400 м.
Способ высокоточного определения высоты полета НЛЦ моноимпульсной РЛС сопровождения, характеризующийся формированием и излучением зондирующих радиолокационных сигналов, приемом отраженных эхо-сигналов от НЛЦ и от подстилающей поверхности и их обработкой с помощью ЭВМ РЛС для определения дальности до НЛЦ, определения высоты ее полета и соответствующего взаимного геометрического расположения РЛС и НЛЦ (см. фиг. 2). Особенностью этого способа является то, что в РЛС используется антенна с 4-мя квадрантами А, В, С, D полотна, реализующими суммарно-разностную обработку по углу места и в наклонной плоскости (см. фиг. 3). При этом для повышения точности определения высоты полета НЛЦ используется дополнительный диагональный разностный канал, который образуется согласно логике (SigA+SigD) -(SigB+SigC), где SigA, SigB, SigD, SigC - сигналы с квадрантов А, В, D, С, причем для получения ненулевого сигнала ошибки Δγ с этого дополнительного диагонального разностного канала при сопровождении НЛЦ в наклонной плоскости выполняется расстройка в наклонной плоскости в βр градусов:
βР=(0,4÷0,6)⋅θ0,5,
где θ0,5 - ширина суммарной ДН антенны РЛС.
Способ осуществляется в 3 последовательных этапа:
на 1-м этапе после развертывания РЛС в точке ее дислокации в память ЭВМ РЛС вводятся точные координаты дислокации РЛС, в том числе, по высоте относительно уровня моря, точное время системы единого времени (СЕВ) с помощью входящего в РЛС спутникового навигатора с атомными часами,
на 2-м этапе с помощью РЛС осуществляют сопровождение НЛЦ, при этом на каждом такте работы РЛС в ЭВМ РЛС запоминаются значения сигнала СС по углу места εЛ, то есть потактно формируется числовой массив (см. фиг. 4, кривая 5). В ЭВМ РЛС потактно анализируется величина сигнала εЛ и при монотонном увеличении величины сигнала СС εЛ, что является признаком начала очередного локального максимума сигнала СС по углу места, на каждом такте работы РЛС в ЭВМ РЛС запоминаются значения модуля сигнала угломестного разностного канала Δv (см. фиг. 4, кривая 7) и значения сигнала ошибки Δγ дополнительного диагонального разностного канала (см. фиг. 4, кривая 6), для чего вход приемного канала РЛС по азимуту периодически переключается на выход этого диагонального разностного канала с антенной системы РЛС с частотой, меньшей, чем основная частота зондирования РЛС. При этом потактно формируются дополнительно еще 2 числовых массива, затем фиксируется момент времени Т2 прохождения сигнала ошибки Δγ диагонального разностного канала через ноль (см. фиг. 4, кривая 6), которому также соответствует момент наступления минимума модуля сигнала угломестного разностного канала Δv, запоминается значение дальности R2 от РЛС до НЛЦ, определяемое РЛС в этот момент Т2, запоминается значение скорости НЛЦ VЦ, определяемое РЛС. Затем в полученном массиве сигнала ошибки Δγ диагонального разностного канала определяется максимум и соответствующий ему момент времени Т1, также в момент времени Т1 определяется дальность от РЛС до НЛЦ R1,
на 3-м этапе на интервале от момента Т1 до момента Т2 определяются сумма сигнала ошибки Δγ диагонального разностного канала SumΔγ в градусах и сумма сигнала СС εЛ по углу места SumTS в градусах, и затем высота полета НЛЦ определяется из целевой функции:
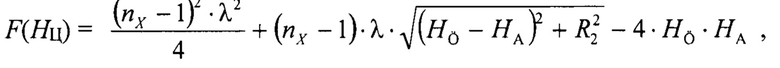
где nx - натуральное число, большее или равное 2 (n=2, 3, 4, 5, …), которое равно неизвестному количеству набегов разности фаз в 180° между прямым сигналом и сигналом, отраженным от подстилающей поверхности;
HA -высота фазового центра антенны РЛС;
НЦ -высота полета НЛЦ;
λ, - длина рабочей волны РЛС метрового, дециметрового или сантиметрового диапазона;
R2 - дальность от РЛС до НЛЦ, соответствующая центру анализируемого локального максимума сигнала СС εЛ по углу места, и определяемая РЛС в момент Т2 минимума модуля сигнала угломестного разностного канала Δv. Затем с помощью одномерного поиска нуля целевой функции F(НЦ) по переменной НЦ определяется ряд возможных высот полета НЛЦ НЦ, каждая из которых соответствует одному из значений переменной nx. После этого для определения истинной высоты полета НЛЦ для каждого полученного значения высоты НЦ запускается программа ЭВМ РЛС движения НЛЦ с тем же значением такта зондирования, со скоростью НЛЦ VЦ и с дальности R1, соответствующей моменту Т1, до дальности R2, соответствующей моменту Т2. В этой программе ЭВМ РЛС используются характеристики антенной системы РЛС, выполняется замыкание обоих СС по углу места и в наклонной плоскости. Эта программа потактно определяет взаимное геометрическое расположение РЛС и НЛЦ, движущейся со скоростью VЦ на высоте НЦ, потактно определяет разность хода и разность фаз прямого луча и сигнала, отраженного от подстилающей поверхности, и вырабатывает сигнал ошибки Δγ диагонального разностного канала и сигнал СС по углу места εЛ с теми же значениями тактов, которые были использованы при работе РЛС. При работе этой программы для каждого полученного с помощью функции F(НЦ) значения высоты НЦ с момента Т1 до момента Т2 определяются значения сумм сигнала ошибки Δγ диагонального разностного канала в градусах и сигнала СС по углу места εЛ в градусах ∑ Δγ и ∑ εЛ (см. фиг. 6). Работа указанной программы прекращается тогда, когда полученное значение суммы ∑ Δγ становится более чем в 4÷5 раз меньше величины SuniΔγ. Затем для значений высоты НЦ, которым соответствуют значения полученных сумм ∑ εЛ, не меньшие половины величины SumTS, значения суммы ∑ Δγ, являющиеся результатом работы этой программы, сравниваются с суммой сигнала ошибки Δγ диагонального разностного канала SumΔγ, которое было получено при работе РЛС. В результате этого определяется ближайшее значение ∑ Δγ к величине SumΔγ, что определяет истинное значение высоты полета НЛЦ НЦ. При этом выполняется регулярное определение высоты полета НЛЦ на каждом очередном локальном максимуме сигнала СС по углу места, и получаемая оценка высоты постоянно уточняется на всем интервале сопровождения НЛЦ.
Сущность заявляемого изобретения состоит в следующем. Особенностью заявляемого способа является то, что в нем не снижается отрицательное влияние явления многолучевости на характер сигнала СС, а, наоборот, используются локальные максимумы сигнала СС по углу места («колокола»), вызванные проникновением сигнала «антипода» в главный луч ДН антенны. Предлагаемый способ не требует изменения высоты антенны РЛС и основан на анализе изменения разности хода (и разности фаз) между прямым сигналом и сигналом «антипода» при движении НЛЦ. Высота полета НЛЦ определяется частично традиционным радиолокационным способом, но без общепринятого прямого измерения угла места этой НЛЦ, выполняемого с помощью относительно сложных парциальных узконаправленных по углу места антенн или с использованием отдельного РЛС-высотомера и др., вместо чего в данном способе применяется значительно более простая 4-квадрантная антенна, которая используется в СС РЛС по углу места и в наклонной плоскости. Высота полета НЛЦ определяется как функция от дальности до НЛЦ, высоты фазового центра антенны РЛС и длины рабочей волны РЛС в момент времени, соответствующий центру анализируемого локального максимума сигнала СС по углу места. С помощью этих данных определяется ряд возможных значений высоты полета НЛЦ, из которого затем вычисляется истинное значение высоты полета с помощью дополнительного диагонального разностного канала.
Способ осуществляется следующим образом.
Рассмотрим простейшую РЛС сопровождения, которая имеет 4-х квадрантную антенну с возможностью поворота ее на любой угол по азимуту согласно полученному целеуказанию. При этом ДН этих квадрантов синхронно управляются. После развертывания РЛС в точке ее дислокации осуществляется ее координатная привязка к единой системе координат ПВО страны с помощью входящего в состав РЛС спутникового навигатора.
Способ осуществляется в 3 последовательных этапа.
На 1-м этапе после развертывания РЛС в точке ее дислокации в память ЭВМ РЛС вводятся с помощью соответствующего пульта точные координаты дислокации РЛС, в том числе, по высоте относительно уровня моря, точное время системы единого времени (СЕВ) с помощью входящего в РЛС спутникового навигатора с атомными часами.
На 2-м этапе после включения РЛС осуществляют с ее помощью радиолокационную работу в выделенном секторе ответственности, в том числе принятие целеуказания о наличии НЛЦ (или нескольких НЛЦ), получение необходимых данных об НЛЦ и фиксирование их в памяти ЭВМ РЛС для вычисления высоты НЦ НЛЦ на 3-м этапе.
Рассмотрим подробнее осуществление способа на 2-м этапе. К основному каналу получения радиолокационной информации (эхо-сигналы, отраженные от НЛЦ и подстилающей поверхности и др.) относятся, в частности, 4-х квадрантная антенна и СС РЛС по углу места и по азимуту. При этом СС формирует упреждающий строб автосопровождения НЛЦ.
Кроме того, для идентификации высоты полета НЛЦ на 3-м этапе используется сигнал ошибки Δγ дополнительного диагонального разностного канала, который формируется согласно логике: (SigA+SigD) - (SigB+SigC), где SigA, SigB, SigC, SigD - сигналы с квадрантов А, В, С, D полотна антенны РЛС (см. фиг. 3). При точном сопровождении НЛЦ по азимуту (в наклонной плоскости) сигнал ошибки Δγ диагонального разностного канала будет равен нулю. Чтобы сигнал ошибки Δγ был отличен от нуля, при сопровождении НЛЦ в наклонной плоскости вводится расстройка сопровождения в βР градусов в наклонной плоскости в пределах ширины ДН антенны:
βР=(0,4÷0,6)⋅θ0,5,
где θ0,5 - ширина суммарной ДН антенны РЛС.
Для идентификации истинной высоты полета НЛЦ из полученного на 3-м этапе ряда возможных высот полета используется явление монотонного уменьшения коэффициента наклона функции сигнала ошибки Δγ диагонального разностного канала, которое происходит при увеличении высоты полета НЛЦ в пределах каждого анализируемого «колокола» (см. фиг. 6).
При работе РЛС очередной «колокол» начинает формироваться при приближении разности фаз между сигналом от НЛЦ и сигналом «антипода» к 180°. В моменты максимумов «колоколов» (см. фиг. 1) разность фаз между сигналом от НЛЦ и сигналом «антипода» становится равной 180°. Так как сигналы близки по мощности, то сигнал суммарного канала стремится к нулю. Модуль сигнала в угломестном разностном канале Δv также стремится к нулю. Поэтому при вычислении сигнала ошибки Δε фазового дискриминатора (ФД) выполняется деление на ноль, то есть возникает сингулярность.
Из-за явления сингулярности вычисляемая угловая ошибка Δε в угломестном канале может достигать очень большой величины, которую будет ограничивать только собственный шум суммарного канала. СС резко увеличивает угол подъема луча εЛ, и образуются «колокола» (см. фиг. 1).
В моменты максимумов «колоколов» (см. фиг. 1) разность фаз между сигналом от НЛЦ и сигналом «антипода» становится равной 180°. Между каждыми соседними локальными максимумами сигнала СС («колоколами») разность хода между сигналами ΔL возрастает на длину рабочей волны РЛС λ, или, что то же самое, разность фаз сигналов увеличивается на 2-я. Эти локальные максимумы («колокола») хорошо различимы при сопровождении НЛЦ.
Минимумы модуля сигнала угломестного разностного канала Δv (см. фиг. 1, кривые 3 и 4) имеют ярковыраженный характер и наблюдаются в 2 раза чаще «колоколов» сигнала СС, причем разность хода ДХ между соседними минимумами модуля сигнала Δv возрастает наполовину длины волны, то есть на λ/2. Минимумам модуля сигнала угломестного разностного канала Δv, расположенным между «колоколами» (см. фиг. 1, кривые 4 - «промежуточные» минимумы) соответствует синфазность прямого сигнала и сигнала «антипода», то есть в этих точках разность фаз между сигналами равна 0°.
С течением времени период следования «колоколов» уменьшается, так как при увеличении угла места НЛЦ εЦ разность хода ΔL (и разность фаз) между прямым сигналом и сигналом «антипода» возрастает все быстрее (см. фиг. 2).
Например, на фиг. 1 приведен типичный вид локальных максимумов сигнала СС по углу места εЛ («колоколов») для плоской Земли - кривая 1 (в градусах), при этом истинный угол места НЛЦ - кривая 2 (в градусах). Высота полета НЛЦ НЦ=200 м, скорость полета НЛЦ VЦ=130 м/с, полетное время (время наблюдения НЛЦ) в секундах отложено по оси абсцисс, коэффициент отражения от подстилающей поверхности ρ≈0,9, длина рабочей волны РЛС λ=0,03 м.
В результате работы СС по углу места в памяти ЭВМ РЛС на каждом такте работы (на каждом зондировании) запоминаются значения сигнала СС по углу места εЛ (см. фиг. 4, кривая 5), при этом потактно формируется числовой массив. Одновременно с этим на каждом такте работы РЛС в ЭВМ РЛС запоминаются значения модуля сигнала угломестного разностного канала Δv (см. фиг. 4, кривая 7) и значения сигнала ошибки Δγ дополнительного диагонального разностного канала (см. фиг. 4, кривая 6). Для этого вход приемного канала РЛС по азимуту периодически переключается на выход этого диагонального разностного канала с антенной системы РЛС с частотой, меньшей, чем основная частота зондирования РЛС. При этом в памяти ЭВМ РЛС потактно формируются дополнительно еще 2 числовых массива.
Затем на 3-м этапе осуществления способа вычисляют собственно высоту полета НЦ НЛЦ. При этом используются данные, зафиксированные в памяти ЭВМ на 1-м и 2-м этапах. Для пояснения достаточно сложного алгоритма вычисления уточним некоторые его моменты.
На фиг. 2 представлена геометрия распространения прямого луча и луча, отраженного от земной поверхности («антипода») для «плоской» Земли.
На фиг. 3 приведено классическое квадратное полотно антенны РЛС (А, В, С, D - квадранты полотна). Суммарно-разностная обработка выполняется по схеме Пейджа. Угломестный разностный канал формируется стандартным образом: (SigA+SigB) - (SigC+SigD), где SigA, SigB, SigC, SigD - сигналы с квадрантов А, В, С, D.
В простейшем варианте работы СС по углу места положение центра луча радиолокатора εЛ на i+1 - м шаге описывается формулой:
εЛ i+1=εЛi+Δεi⋅Dε⋅Δt,
где Dε - добротность СС (коэффициент усиления сигнала ошибки);
εЛ i - положение луча на i - м шаге;
Δεi - сигнал ошибки фазового дискриминатора (ФД) угломестного канала на i-м шаге;
Δt - величина такта зондирования.
Из рассмотрения разности ходов прямого и отраженного сигналов (см. фиг. 2), соответствующих разностей фаз для центра некоторого анализируемого «колокола» и учитывая дополнительный сдвиг фазы при отражении на π, записывается следующее равенство:

где λ - длина рабочей волны радиолокатора;
nx - натуральное число, большее или равное 2, которое равно неизвестному количеству набегов разности фаз в 180° между прямым сигналом и сигналом «антипода».
Раскрывая скобки, получаем:

Возводим в квадрат обе части и используем теорему Пифагора:

Окончательно получаем целевую функцию для «плоской» Земли:
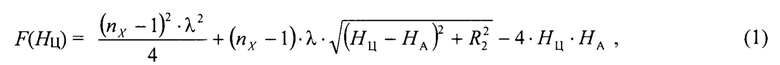
где HA - высота фазового центра антенны РЛС;
НЦ -высота полета НЛЦ;
R2 - дальность, соответствующая центру анализируемого «колокола».
Так как заранее неизвестно, сколько раз произошел набег разности фаз в 180° для анализируемого «колокола», то в функции F(НЦ) (1) присутствует неизвестная целая переменная nx. При изменении значения их на 1 разность фаз сигналов изменяется на 180°.
Значение дальности R2 измеряется РЛС по ярко выраженному минимуму модуля сигнала угломестного разностного канала Δv (см. фиг. 4, кривые 7). Кривая 5 (см. фиг. 4) - сигнал СС εЛ по углу места. Высота полета НЛЦ НЦ=100 м, скорость НЛЦ VЦ=65 м/с. Начальная горизонтальная дальность RГ-НАЧ=42 км. Конечная горизонтальная дальность Rг_кон=3000 м. ЭПР НЛЦ σЦ ≈ 2 м2. Высота фазового центра антенны HA=5,5 м. Рабочая длина волны РЛС λ=0,03 м. Временной интервал наблюдения TНАБЛ=600 с. Отношение сигнал/шум на дальности 42 км ρСШ ≈ 40 дБ. Добротность СС по углу места Dε=5, такт зондирования Δt=0,1 с. По оси абсцисс отложено полетное время в секундах.
С помощью одномерного поиска нуля целевой функции F(НЦ) (1) попеременной НЦ вычисляется ряд возможных высот полета НЛЦ НЦ, каждая из которых соответствует одному из значений переменной nx. Значение nx при этом может достигать 8÷10 и более.
Коэффициент зеркального отражения ρ∑ вычисляется по формуле [«Справочник по радиолокационным измерениям». Д. Бартон, Г. Вард. Москва, «Советское радио», 1976 г.]:

где ρ0(ψ) - коэффициент отражения для гладкой поверхности, зависит от угла ψ;
ρS - коэффициент отражения от неровной поверхности.
Сферическая расходимость радиоволн не учитывается: КСФ=1 [«Теоретические основы радиолокации», под ред. В.Е. Дулевича, Москва, «Советское радио», 1978 г., «Справочник по радиолокации в 2 книгах», под. ред. М.И. Сколника. Москва, «Техносфера», 2014 г., Lamont V.Blake, "Machine Plotting of Radio/Radar Vertical-Plane Coverage Diagrams". Naval Research Laboratory, Washington, D. C, 1970].
Коэффициент отражения от неровной поверхности ρS вычисляется по формуле [«Справочник по радиолокационным измерениям». Д. Бартон, Г. Вард. Москва, «Советское радио», 1976 г., «Справочник по радиолокации в 2 книгах», под. ред. М.И. Сколника. Москва, «Техносфера», 2014 г., Lamont V.Blake, "Machine Plotting of Radio/Radar Vertical-Plane Coverage Diagrams". Naval Research Laboratory, Washington, D. C., 1970]:
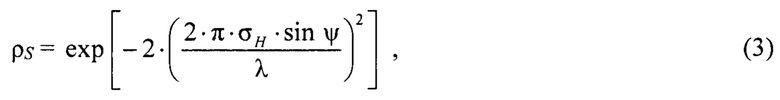
где σH - среднеквадратичное значение отклонения высоты поверхности;
ψ - угол скольжения.
Характер изменения коэффициента отражения от гладкой поверхности ρ0(ψ) [«Справочник по радиолокации в 4 томах, т. 1», под. ред. М.И. Сколника. Москва, «Советское радио», 1976 г., «Справочник по радиолокации в 2 книгах», под. ред. М.И. Сколника. Москва, «Техносфера», 2014 г., Lamont V.Blake, "Machine Plotting of Radio/Radar Vertical-Plane Coverage Diagrams". Naval Research Laboratory, Washington, D. C., 1970] аппроксимируется выражением:
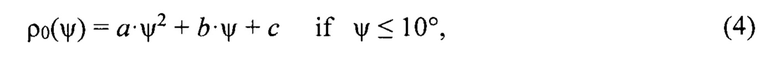
где a=0,0108642; b=-0,19555556; c=1,0.
Фаза при отражении равна ϕОТР=180°, так как угол скольжения ψAHT≤5° [«Справочник по радиолокации в 4 томах, т.1», под. ред. М.И. Сколника. Москва, «Советское радио», 1976 г., «Справочник по радиолокации в 2 книгах», под. ред. М.И. Сколника. Москва, «Техносфера», 2014 г., Lamont V.Blake, "Machine Plotting of Radio/Radar Vertical-Plane Coverage Diagrams". Naval Research Laboratory, Washington, D. C., 1970].
На фиг. 5 приведена кривая изменения коэффициента зеркального отражения ρ∑ при высоте полета НЛЦ НЦ=100 м и скорости полета VЦ=65 м/с, полученная при значении σH=0,2 м, которое соответствует волнению моря в 2 балла [«Справочник по радиолокационным измерениям». Д. Бартон, Г. Вард. Москва, «Советское радио», 1976 г.].
Априори неизвестен номер конкретного анализируемого «колокола» (считая с момента выхода НЛЦ из-за радиогоризонта) - то есть неизвестно количество набегов разности фаз по 360°, поэтому для определения истинной высоты полета НЛЦ проверяется весь полученный ряд высот НЛЦ НЦ для каждого значения nx (1).
Для идентификации истинной высоты полета НЛЦ используется сигнал ошибки Δγ дополнительного диагонального разностного канала (см. фиг. 4, кривая 6), который формируется согласно логике: (SigA+SigD) - (SigB+SigC), где SigA, SigB, SigC, SigD - сигналы с квадрантов А, В, С, D полотна антенны РЛС (см. фиг. 3). Но при точном сопровождении НЛЦ по азимуту (в наклонной плоскости) сигнал ошибки Δγ диагонального разностного канала будет равен нулю. Чтобы сигнал ошибки Δγ был отличен от нуля, при сопровождении НЛЦ в наклонной плоскости вводится небольшая расстройка сопровождения в βP градусов в наклонной плоскости в пределах ширины ДН антенны:
βP=(0,4÷0,6)⋅θ0,5,
где θ0,5 - ширина суммарной ДН антенны РЛС.
Кривая 6 на фиг. 4 - сигнал ошибки Δγ диагонального разностного канала. Нулевые значения сигнала ошибки Δγ по времени точно совпадают с минимумами модуля сигнала угломестного разностного канала Δv (см. фиг. 4, кривые 7). Кривые на фиг. 4 получены при величине расстройки в наклонной плоскости βP=0,4°.
Каждая пара максимумов и минимумов сигнала ошибки Δγ соответствует каждому «колоколу» сигнала СС по углу места εЛ. Локальные экстремумы сигнала ошибки Δγ находятся в точках перегиба функции εЛ (t), где 2-ая производная функции εЛ (t) меняет знак. С увеличением высоты полета НЛЦ разница между углами на НЛЦ и на «антипод» все более увеличивается, сигнал «антипода» выходит из главного лепестка ДН антенны РЛС, и его влияние все более уменьшается. Это приводит к пропорциональному уменьшению сигнала ошибки Δγ (см. фиг. 6). Кривые 8, 9, 10, 11 на фиг. 6 - это кривые сигнала ошибки Δγ, которые соответствуют значениям высоты полета НЛЦ: НЦ=100 м, 200 м, 300 м, 400 м для 1-го «колокола» сигнала СС (см. фиг. 4, кривая 5). Центр этого «колокола» приблизительно соответствует временной отметке в 82,1 с, скорость НЛЦ равна VЦ=65 м/с. Высоты полета НЛЦ кратны значению 100 м.
Каждому значению высоты полета НЛЦ НЦ строго соответствует своя кривая сигнала ошибки Δγ. В пределах каждого «колокола» функция сигнала ошибки Δγ является нечетной симметричной функцией относительно своего нулевого значения, что отвечает требованиям, предъявляемым к пеленгационной характеристике (см. фиг. 4, кривая 6).
С увеличением высоты полета НЛЦ коэффициент наклона функции сигнала ошибки Δγ дополнительного диагонального разностного канала монотонно уменьшается в пределах каждого анализируемого «колокола» (см. фиг. 6, кривые 8, 9, 10, 11). Указанная особенность функции сигнала ошибки Δγ диагонального разностного канала позволяет его использовать для идентификации номера конкретного анализируемого «колокола» (считая с момента выхода НЛЦ из-за радиогоризонта), то есть для определения истинной высоты полета НЛЦ НЦ из полученного с помощью целевой функции F(НЦ) (1) ряда высот.
Для уменьшения влияния различных помех и шумов при определении высоты полета НЛЦ вычисляется значение площади под кривой сигнала ошибки Δγ между 1-м максимумом сигнала Δγ, по времени это приблизительно 28 с на фиг. 6, и минимумом модуля сигнала угломестного разностного канала Δv, соответствующего центру анализируемого «колокола».
Рассмотрим осуществление способа на следующем примере.
Высота полета НЛЦ НЦ=200 м, скорость НЛЦ VЦ = 65 м/с. Начальная горизонтальная дальность RГ_НАЧ=42 км. Конечная горизонтальная дальность RГ_КОН=3000 м. Эффективная поверхность рассеяния НЛЦ σЦ ≈ 2 м2. Высота фазового центра антенны HA=5,5 м. Ширина ДН одного квадранта θ0,5 ≈ 1,342°, ширина суммарной ДН θ0,5 ≈ 0,8553°. База антенны РЛС dРЛС ≈ 0,838 м, крутизна пеленгационной характеристики угломестного канала KA=1,056 1/градус, крутизна пеленгационной характеристики диагонального разностного канала KA=1,056 1/градус. Рабочая длина волны РЛС λ=0,03 м. Временной интервал наблюдения TНАБЛ=600 с. Отношение сигнал/шум на дальности 42 км ρСШ ≈ 40 дБ. Величина расстройки в наклонной плоскости βP=0,4°. Добротность СС Dε=5, такт зондирования Δt=0,1 с. Волнение моря 2 балла, ему соответствует с. к. о. высоты поверхности σH=0,2 м.
Анализируется 1-ый «колокол» сигнала СС по углу места (см. фиг. 4, кривая 5), которому соответствует отрезок времени приблизительно от 30 с до 140 с.
Первому максимуму сигнала ошибки Δγ соответствует момент времени Т1 ≈ 28,0 с. Середине «колокола» соответствует момент времени T2≈82,1 с, при этом горизонтальная дальность RГ ≈ 36663,5 м. Момент времени Т2 определяется по моменту прохождения сигнала ошибки Δγ диагонального разностного канала через ноль (см. фиг. 4, кривая 6).
Из полученных на 2-м этапе осуществления способа числовых массивов сигналов Δγ и εЛ вычисляются суммы сигналов в градусах ∑ Δγ и ∑ εЛ от 1-го максимума сигнала Δγ до середины «колокола»:
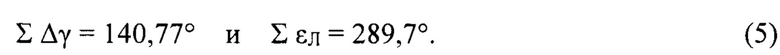
Поиск нуля целевой функции F(НЦ) (1) дает следующий набор возможных высот полета НЛЦ HЦ: 50 м, 100 м, 150 м, 200 м, 250 м, 300 м, 350 м, 400 м, 450 м, 500 м, 550 м, 600 м и т.д. Начиная с высоты 50 м проверяется полученный ряд высот НЛЦ НЦ. При этом для каждого значения высоты запускается программа ЭВМ РЛС, определяющая движение НЛЦ со скоростью VЦ=65 м/с с дальности R1, соответствующей моменту Т1 максимума сигнала ошибки Δγ для «анализируемого» «колокола», до дальности R1, соответствующей центру анализируемого «колокола» - моменту Т2. Величина такта зондирования Δt=0,1 с. Характеристики антенной системы в этой программе максимально близки к характеристикам антенной системы РЛС. При работе программы выполняется замыкание обоих СС по углу места и в наклонной плоскости. Указанная программа потактно определяет взаимное геометрическое расположение РЛС и НЛЦ, движущейся со скоростью VЦ на высоте НЦ, потактно определяет разность хода и разность фаз прямого луча и сигнала «антипода», и вырабатывает сигнал ошибки Δγ диагонального разностного канала и сигнал СС по углу места εЛ с теми же значениями тактов, которые были использованы при работе РЛС.
По формулам (2÷4) вычисляется значение коэффициента отражения ρ∑ для каждого значения угла скольжения ψ, при этом для моря величина с. к. о. высоты поверхности σH определяется экспериментально в зависимости от волнения моря в баллах. Учитывая возможную ошибку при определении он, при работе программы используются значения он с разбросом ±10%: σH=0,18 м и σH=0,22 м.
При работе этой программы для каждого полученного значения высоты НЦ с момента Т1 до момента Т2 определяются значения сумм сигнала ошибки Δγ диагонального разностного канала в градусах и сигнала СС по углу места εЛ в градусах: ∑ Δγ и ∑ εЛ.
В результате работы программы для каждого значения НЦ вычисляются значения сумм ∑ Δγ и ∑ЕεЛ (см. табл.1).
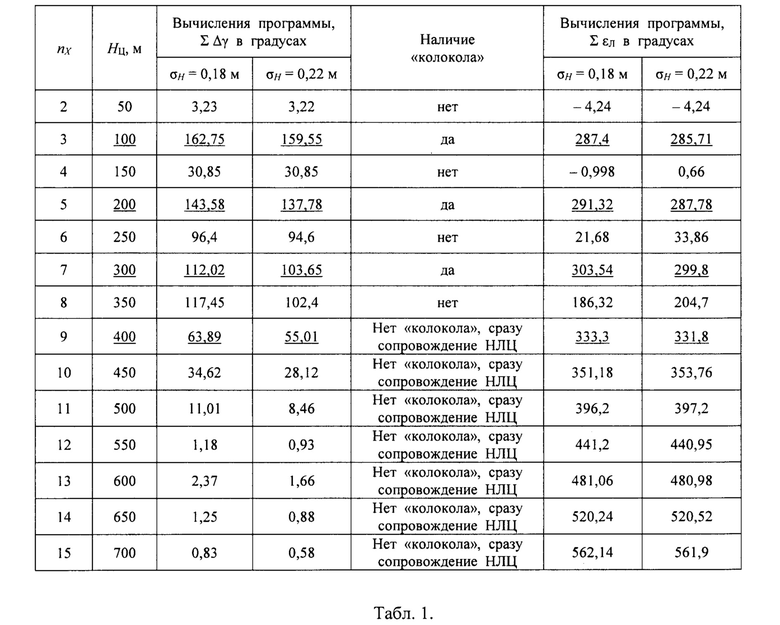
Высоты, превышающие 700 м, не проверяются, так как величина суммы ∑ Δγ уменьшается более чем в 4 раза по сравнению с контрольным значением ∑ Δγ=140,77° (5). Далее величина этой суммы только убывает. Сигнал «антипода» выходит из основного лепестка ДН антенны РЛС, его влияние резко падает, «колокола» больше не образуются, и главный лепесток суммарной ДН антенны РЛС начинает сопровождать сигнал от НЛЦ с малыми ошибками. С выходом сигнала «антипода» из основного лепестка ДН сигнал ошибки Δγ диагонального разностного канала стремится к нулю. На фиг. 4 этому моменту соответствует время приблизительно 525 с.
Однако нет необходимости проверять все высоты с шагом 50 м. Из анализа формулы (1) следует, что «колокола» могут присутствовать только при изменении разности фаз между сигналами на 360°, то есть через одно значение nx (для нечетных значений nx). Данные табл. 1 подтверждают это. Величина полученной суммы ∑ εЛ показывает, что «колокола» существуют только для значений nx=3, 5, 7 (в табл. 1 данные для этих высот подчеркнуты). Для высот 400 м, 500 м, 600 м, 700 м и выше «колокола» уже не образуются, так как сигнал «антипода» выходит из основного лепестка ДН антенны РЛС.
Анализ полученных данных (см. табл. 1) показывает, что только для высоты полета НЦ=200 м (nx=5) диапазон полученных значений ∑ Дγ=137,78°+143,58° включает в себя контрольное значение ∑ Δγ=140,77° (5), которое является результатом работы РЛС. Это указывает, что высота полета НЛЦ составляет НЦ ≈ 200 м.
Предлагаемый способ позволяет выполнить вычисление высоты полета НЛЦ НЦ за половину времени длительности анализируемого «колокола».
В предлагаемом способе при вычислении высоты полета НЛЦ контур сопровождения СС по углу места не разрывается, что позволяет увеличить дальность сопровождения НЛЦ.
Предложенный способ не требует знания номера «колокола» сигнала СС по углу места с момента выхода НЛЦ из-за радиогоризонта, то есть не нужна информация о количестве набегов разности фаз в 180° между прямым сигналом и сигналом «антипода».
Для применения предлагаемого способа при сопровождении НЛЦ необходимо ожидать появления «колокола». Чтобы быстрее обнаружить «колокол», рекомендуется изменять рабочую длину волны РЛС λ. Изменение длины волны на 10%-20% и более позволяет существенно изменять положение очередного «колокола» во времени. Уменьшение длины волны вызывает более раннее появление «колокола», увеличение длины волны приводит к запаздыванию появления «колокола».
В заявляемом способе точность определения высоты полета НЛЦ в основном определяется точностью определения дальности R, соответствующей центру анализируемого «колокола», которая поступает от РЛС при сопровождении НЛЦ. Кроме того, в заявляемом способе не требуется проведение каких-либо конструктивных или аппаратурных изменений в РЛС, введения дополнительной квадратурной обработки, изменения высоты антенны РЛС и т.д.
Для получения сигнала ошибки Δγ диагонального разностного канала вход приемного канала РЛС по азимуту периодически переключается на выход этого диагонального разностного канала с антенной системы РЛС с частотой, меньшей, чем основная частота зондирования РЛС.
Для корабельных РЛС, береговых РЛС или при наличии другой, относительно ровной подстилающей поверхности предлагаемый способ особенно эффективен. При волнении моря не выше 2-3 баллов можно считать, что поверхность моря представляет собой практически идеальную сферу. При малых углах места коэффициент отражения ρ0 близок к 1, влияние неровностей поверхности сводится к минимуму, поэтому локальные максимумы сигнала СС по углу места («колокола»), сигнал ошибки Δγ дополнительного диагонального разностного канала и минимумы модуля сигнала угломестного разностного канала Δv хорошо акцентированы.

Изобретение относится к радиолокации и может быть использовано в радиолокационной станции (РЛС) сопровождения низколетящих целей (НЛЦ) под малыми углами места при наличии мешающих отражений от подстилающей поверхности. Техническим результатом является повышение точности определения высоты полета НЛЦ при одновременном упрощении конструкции антенной системы РЛС. В заявленном способе осуществляют излучение зондирующих радиолокационных сигналов, прием отраженных эхо-сигналов от НЛЦ и от подстилающей поверхности и их обработку для определения дальности до НЛЦ, высоты ее полета и взаимного геометрического расположения РЛС и НЛЦ. При этом в РЛС используется антенна с 4-мя квадрантами А, В, С, D полотна, реализующими суммарно-разностную обработку по углу места и в наклонной плоскости. Используется дополнительный диагональный разностный канал, причем для получения ненулевого сигнала ошибки Аγ с этого дополнительного канала при сопровождении НЛЦ в наклонной плоскости выполняется расстройка в наклонной плоскости в βр градусов. Способ осуществляется в 3 последовательных этапа: на 1-м этапе в память ЭВМ РЛС вводятся точные координаты дислокации РЛС, на 2-м этапе с помощью РЛС осуществляют сопровождение НЛЦ, на каждом такте работы РЛС в ЭВМ РЛС запоминают значения модуля сигнала угломестного разностного канала Δv и значения сигнала ошибки Δγ дополнительного диагонального разностного канала, запоминают значение дальности R2 от РЛС до цели, значение скорости цели VЦ, определяемое РЛС, затем в полученном массиве сигнала ошибки Δγ диагонального разностного канала определяется максимум и соответствующий ему момент времени Т1, в который определяется дальность от РЛС до цели R1, на 3-м этапе определяют сумму сигнала ошибки Δγ диагонального разностного канала SumΔγ в градусах и сумму сигнала следящей системы (СС) εЛ по углу места SumTS в градусах, и затем определяют высоту полета цели, и в результате обработки определяют истинное значение высоты полета НЛЦ НЦ. 1 табл., 6 ил.
Способ высокоточного определения высоты полета низколетящей цели моноимпульсной РЛС сопровождения, характеризующийся формированием и излучением зондирующих радиолокационных сигналов, приемом отраженных эхо-сигналов от низколетящей цели (НЛЦ) и от подстилающей поверхности и их обработкой с помощью ЭВМ РЛС для определения дальности до НЛЦ, определения высоты ее полета и соответствующего взаимного геометрического расположения РЛС и НЛЦ, отличающийся тем, что в РЛС используется антенна с 4-мя квадрантами А, В, С, D полотна, реализующими суммарно-разностную обработку по углу места и в наклонной плоскости, при этом для повышения точности определения высоты полета НЛЦ используется дополнительный диагональный разностный канал, который образуется согласно логике (SigA+SigD) - (Sigв+SigC), где SigA, SigB, SigD, SigC - сигналы с квадрантов А, В, D, С, причем для получения ненулевого сигнала ошибки Аγ с этого дополнительного диагонального разностного канала при сопровождении НЛЦ в наклонной плоскости выполняется расстройка в наклонной плоскости в βP градусов:
βP=(0,4÷0,6)⋅θ0,5,
где θ0,5 - ширина суммарной диаграммы направленности антенны РЛС, при этом способ осуществляется в 3 последовательных этапа: на 1-м этапе после развертывания РЛС в точке ее дислокации в память ЭВМ РЛС вводятся точные координаты дислокации РЛС, в том числе, по высоте относительно уровня моря, точное время системы единого времени (СЕВ) с помощью входящего в РЛС спутникового навигатора с атомными часами, на 2-м этапе с помощью РЛС осуществляют сопровождение НЛЦ, при этом на каждом такте работы РЛС в ЭВМ РЛС запоминаются значения сигнала следящей системы (СС) по углу места εЛ, то есть потактно формируется числовой массив, в ЭВМ РЛС потактно анализируется величина сигнала εЛ и при монотонном увеличении величины сигнала СС εЛ, что является признаком начала очередного локального максимума сигнала СС по углу места, на каждом такте работы РЛС в ЭВМ РЛС запоминаются значения модуля сигнала угломестного разностного канала Δv и значения сигнала ошибки Δγ дополнительного диагонального разностного канала, для чего вход приемного канала РЛС по азимуту периодически переключается на выход этого диагонального разностного канала с антенной системы РЛС с частотой, меньшей, чем основная частота зондирования РЛС, при этом потактно формируются дополнительно еще 2 числовых массива, затем фиксируется момент времени Т2 прохождения сигнала ошибки Δγ диагонального разностного канала через ноль, которому также соответствует момент наступления минимума модуля сигнала угломестного разностного канала Δv, запоминается значение дальности R2 от РЛС до цели, определяемое РЛС в этот момент Т2, запоминается значение скорости цели VЦ, определяемое РЛС, затем в полученном массиве сигнала ошибки Δγ диагонального разностного канала определяется максимум и соответствующий ему момент времени Т1, также в момент времени Т1 определяется дальность от РЛС до цели R1, на 3-м этапе на интервале от момента Т1 до момента Т2 определяются сумма сигнала ошибки Δγ диагонального разностного канала SumΔγ в градусах и сумма сигнала СС εЛ по углу места SumTS в градусах, и затем высота полета цели определяется из целевой функции:
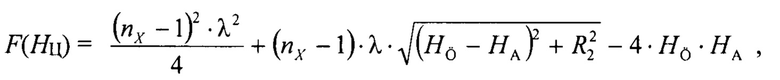
где nx - натуральное число, большее или равное 2, которое равно неизвестному количеству набегов разности фаз в 180° между прямым сигналом и сигналом, отраженным от подстилающей поверхности;
HA - высота фазового центра антенны РЛС;
НЦ - высота полета цели;
λ - длина рабочей волны РЛС метрового, дециметрового или сантиметрового диапазона;
R2 - дальность от РЛС до цели, соответствующая центру анализируемого локального максимума сигнала СС εЛ по углу места, и определяемая РЛС в момент Т2 минимума модуля сигнала угломестного разностного канала Δv, затем с помощью одномерного поиска нуля целевой функции F(НЦ) по переменной НЦ определяется ряд возможных высот полета цели НЦ, каждая из которых соответствует одному из значений переменной nx, затем для определения истинной высоты полета НЛЦ для каждого полученного значения высоты НЦ запускается программа ЭВМ РЛС движения цели с тем же значением такта зондирования, со скоростью цели VЦ и с дальности R1, соответствующей моменту Т1, до дальности R2, соответствующей моменту Т2, в этой программе ЭВМ РЛС используются характеристики антенной системы РЛС, выполняется замыкание обоих СС по углу места и в наклонной плоскости, эта программа потактно определяет взаимное геометрическое расположение РЛС и НЛЦ, движущейся со скоростью VЦ на высоте НЦ, потактно определяет разность хода и разность фаз прямого луча и сигнала, отраженного от подстилающей поверхности, и вырабатывает сигнал ошибки Δγ диагонального разностного канала и сигнал СС по углу места εЛ с теми же значениями тактов, которые были использованы при работе РЛС, при работе этой программы для каждого полученного с помощью функции F(НЦ) значения высоты НЦ с момента Т1 до момента Т2 определяются значения сумм сигнала ошибки Δγ диагонального разностного канала в градусах и сигнала СС по углу места εЛ в градусах ∑ Δγ и ∑ εЛ, работа указанной программы прекращается тогда, когда полученное значение суммы ∑ Δγ становится более чем в 4÷5 раз меньше величины SumΔγ, далее для значений высоты НЦ, которым соответствуют значения полученных сумм ∑ εЛ, не меньшие половины величины SumTS, значения суммы ∑ Δγ, являющиеся результатом работы этой программы, сравниваются с суммой сигнала ошибки Δγ диагонального разностного канала SumΔγ, которое было получено при работе РЛС, в результате чего определяется ближайшее значение ∑ Δγ к величине SumΔγ, что определяет истинное значение высоты полета НЛЦ НЦ, при этом регулярно определяют высоту полета НЛЦ на каждом очередном локальном максимуме сигнала СС по углу места и постоянно уточняют получаемую оценку высоты на всем интервале сопровождения НЛЦ.
| СПОСОБ ОПРЕДЕЛЕНИЯ ТРАЕКТОРИИ ДВИЖЕНИЯ НИЗКОЛЕТЯЩИХ ЦЕЛЕЙ | 2017 |
|
RU2667484C1 |
| Способ точного сопровождения по углу места низколетящей цели в условиях интерференции | 2017 |
|
RU2682239C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛА МЕСТА И ДАЛЬНОСТИ НИЗКОЛЕТЯЩЕЙ ЦЕЛИ МОНОИМПУЛЬСНЫМ РАДИОЛОКАТОРОМ ПРИ МНОГОЛУЧЕВОМ РАСПРОСТРАНЕНИИ ОТРАЖЕННОГО ОТ ЦЕЛИ СИГНАЛА | 1994 |
|
RU2080619C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОМЕСТНОЙ КООРДИНАТЫ НИЗКОЛЕТЯЩЕЙ ЦЕЛИ | 2010 |
|
RU2444750C2 |
| СПОСОБ СОПРОВОЖДЕНИЯ ЦЕЛИ И УСТРОЙСТВО МОНОИМПУЛЬСНОЙ РЛС, РЕАЛИЗУЮЩЕЙ СПОСОБ | 2007 |
|
RU2338219C1 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛА МЕСТА НИЗКОЛЕТЯЩЕЙ ЦЕЛИ И РАДИОЛОКАЦИОННАЯ СТАНЦИЯ ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2307375C1 |
| БАЛАГУРОВСКИЙ В.А., КОНДРАТЬЕВ А.С., ПОЛИЩУК Н.П | |||
| Метод определения координат низколетящей цели // Радиотехника и электроника, 2012, Т | |||
| Способ получения на волокне оливково-зеленой окраски путем образования никелевого лака азокрасителя | 1920 |
|
SU57A1 |
| ПОКРОВСКАЯ Е.А | |||
| Работа | |||
Авторы
Даты
2022-08-30—Публикация
2021-06-08—Подача