Изобретение относится к технике измерения параметров микроволновых линий, в частности к определению геометрических размеров цилиндрического резонатора.
Известен способ определения длины микроволновой линии
(А.С. СССР №1815614, опубликовано 15.05.1993, МПК G01R 27/26), где повышение точности достигается за счет определения пространственного положения в линии трех возбуждаемых резонансных колебаний, соответствующих соседним резонансным частотам одного типа волн, уточнения частотной зависимости критической частоты и линейного положения нулей. В данном способе не определена процедура определения типа колебаний, что снижает точность определения длины линии.
Наиболее близким техническим решением является способ, изложенный в источнике: Егоров В.Н., Токарева Е.Ю., Ле Куанг Туен. Измерение внутренних размеров сверхвысокочастотных объемных резонаторов. Измерительная техника. 2020, №10, с. 65-72. В котором для повышения точности определения геометрических размеров резонатора используются соседние частоты одного типа. Недостатком данного способа является зависимость точности определения длины резонатора от точности определения типа резонансных колебаний, используемых для определения параметров резонатора, а так как в предложенных методах отсутствует процедура определения типа колебаний, соответствующих резонансным частотам, используемым для определения геометрических размеров резонатора, то и точность известных способов не может быть высокой.
Техническим результатом изобретения является повышение точности определения геометрических параметров объемного цилиндрического резонатора за счет введения процедуры определения типов резонансных колебаний, возбуждаемых в резонаторе и определения по ним геометрических размеров цилиндрического резонатора.
Указанная задача решается тем, что предложен способ определения геометрических размеров цилиндрического резонатора, включающий измерение резонансных частот, возбуждаемых в резонаторе и определение по резонансным частотам геометрических размеров резонатора, отличающийся тем, что измеряется частотный спектр амплитудного коэффициента передачи через резонатор резонансных частот из которого определяют величины резонансных частот и их типы волн для приближенно известных размеров длины (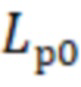 ) и радиуса (
) и радиуса (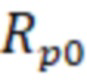 ) резонатора, за тем выбирают любые две резонансные частоты по которым определяют радиус резонатора по формуле:
) резонатора, за тем выбирают любые две резонансные частоты по которым определяют радиус резонатора по формуле:
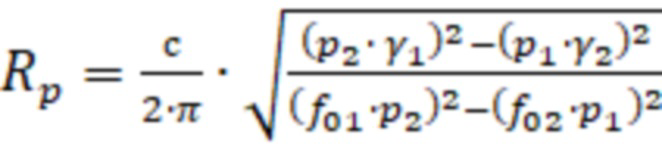 , (1)
, (1)
где 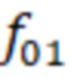 – первая резонансная частота;
– первая резонансная частота;
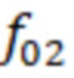 – вторая резонансная частота;
– вторая резонансная частота;
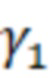 – это
– это 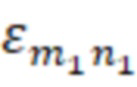 или
или 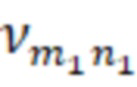 ;
;
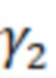 – это
– это 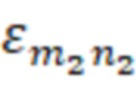 или
или 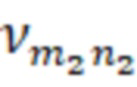 ;
;
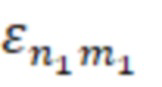 – корни функций Бесселя, соответствующие волнам ТН–типа с критической длиной волны равной
– корни функций Бесселя, соответствующие волнам ТН–типа с критической длиной волны равной 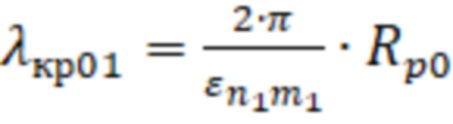 , или
, или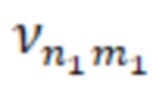 – корни производных функций Бесселя, соответствующих волнам ТЕ–типа с критической длиной волны равной
– корни производных функций Бесселя, соответствующих волнам ТЕ–типа с критической длиной волны равной 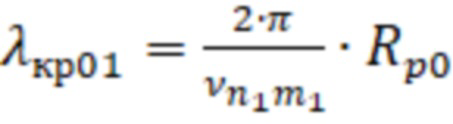 , для первой резонансной частоты;
, для первой резонансной частоты;
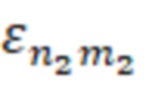 – корни функций Бесселя, соответствующие волнам ТН–типа с критической длиной волны равной
– корни функций Бесселя, соответствующие волнам ТН–типа с критической длиной волны равной 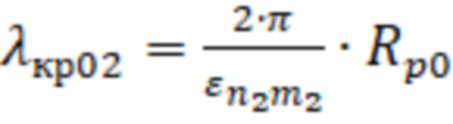 , или
, или 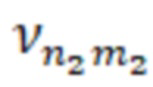 – корни производных функций Бесселя, соответствующих волнам ТЕ–типа с критической длиной волны равной
– корни производных функций Бесселя, соответствующих волнам ТЕ–типа с критической длиной волны равной 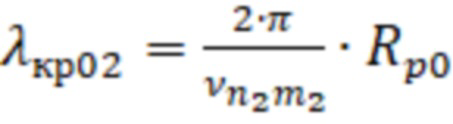 , для второй резонансной частоты;
, для второй резонансной частоты;
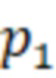 – число вариаций поля по длине резонатора, для первой резонансной частоты;
– число вариаций поля по длине резонатора, для первой резонансной частоты;
m1=0,1…M1 – число вариаций поля по радиусу, порядковый номер функции Бесселя, для первой резонансной частоты;
n1=1,2,…N1 – число вариаций поля по углу вдоль азимута, , для первой резонансной частоты;
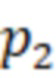 – число вариаций поля по длине резонатора, для второй резонансной частоты;
– число вариаций поля по длине резонатора, для второй резонансной частоты;
m2=0,1…M2 – число вариаций поля по радиусу, порядковый номер функции Бесселя, для первой резонансной частоты;
n2=1,2,…N2 – число вариаций поля по углу вдоль азимута, , для первой резонансной частоты;
с – скорость света;
 – константа;
– константа;
и определяют длину резонатора по формуле:
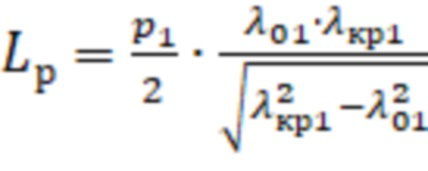 , (2)
, (2)
где 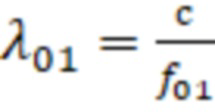 – длина волны на первой резонансной частоте;
– длина волны на первой резонансной частоте;
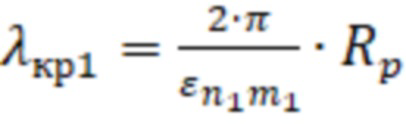 – критическая длина волны, соответствующая волнам ТН–типа или
– критическая длина волны, соответствующая волнам ТН–типа или 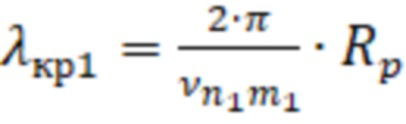 – критическая длина волны, соответствующая волнам ТЕ–типа, для первой резонансной частоты.
– критическая длина волны, соответствующая волнам ТЕ–типа, для первой резонансной частоты.
Авторы установили, что при определении геометрических размеров цилиндрического резонатора известными методами стоячих волн используются колебания на резонансных частотах одного типа, без указания процедуры их определения из частотного спектра амплитудного коэффициента передачи через резонатор, состоящую из множества резонансных частот разных типов волн. Так же в процессе анализа метода стоячих волн в резонаторе была установлена взаимная зависимость между резонансными колебаниями различных типов, которая теоретически описана при формировании структуры полей в полости резонатора в зависимости от геометрических размеров резонатора и для различных постоянных распространения определяется поперечными размерами.
Поэтому авторами предложена процедура определения типов колебаний, соответствующих резонансным частотам спектра амплитудного коэффициента передачи через объемный цилиндрический резонатор, когда после априорных измерений приближенно известны размеры длины (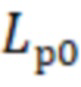 ) и радиуса (
) и радиуса (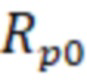 ) резонатора
) резонатора
Из анализа теоретического описания структуры полей, например, в объемном цилиндрическом резонаторе (источник А.Л. Фельдштейн, Л.Р. Явич, В.П. Смирнов. Справочник по элементам волноводной техники.
М, Советское радио, 1966 г. 653 с.) видно, что отличие между типами волн определяется постоянными распространения и, то есть, 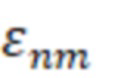 – корнями функций Бесселя , соответствующими волнам ТН–типа с критической длиной волны равной
– корнями функций Бесселя , соответствующими волнам ТН–типа с критической длиной волны равной 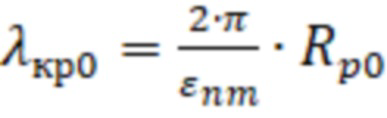 , или
, или 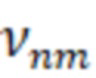 – корнями производных функций Бесселя, соответствующими волнам ТЕ–типа с критической длиной волны равной
– корнями производных функций Бесселя, соответствующими волнам ТЕ–типа с критической длиной волны равной 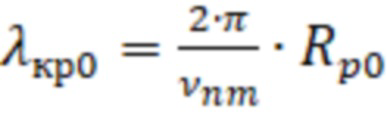 , где n – число вариаций поля по углу вдоль азимута, m – число вариаций поля по радиусу, порядковый номер функции Бесселя.
, где n – число вариаций поля по углу вдоль азимута, m – число вариаций поля по радиусу, порядковый номер функции Бесселя.
С другой стороны, из приведенных теоретических описаний структуры полей волн становится понятно, что различные типы волн связаны между собой и определяются геометрическими параметрами полости резонатора, например, для цилиндрического резонатора, его радиусом и длиной.
Поэтому для определения геометрических параметров полости резонатора можно использовать различные типы волн резонансных колебаний, а так как при определении в частотном спектре амплитудного коэффициента передачи через резонатор типов резонансных частоты необходимо априорное приближенное знание длины резонатора, то для определения геометрических параметров полости резонатора не обязательно использовать соседние резонансные частоты, которые для одного типа волн могут и не наблюдаться Поэтому анализ различных резонансных пар из частотного спектра амплитудного коэффициента передачи через объемный цилиндрический резонатор позволяет многократно определять геометрические параметры полости резонатора, чем также повышать точность определения геометрических параметров полости резонатора.
По паре резонансных частот, выбранных из спектра амплитудного коэффициента передачи через резонатор, определяется радиус резонатора по формуле:
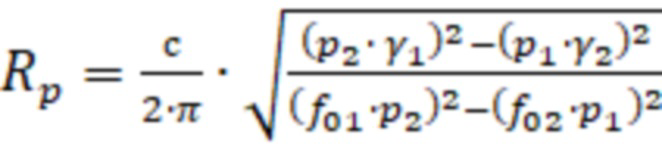 , (1)
, (1)
где 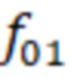 – первая резонансная частота;
– первая резонансная частота;
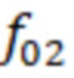 – вторая резонансная частота;
– вторая резонансная частота;
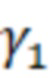 – это
– это 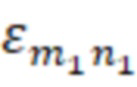 или
или 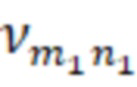 ;
;
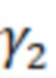 – это
– это 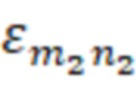 или
или 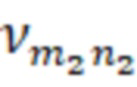 ;
;
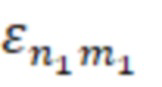 – корни функций Бесселя, соответствующие волнам ТН–типа с критической длиной волны равной
– корни функций Бесселя, соответствующие волнам ТН–типа с критической длиной волны равной 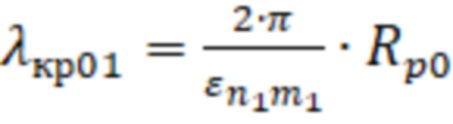 , или
, или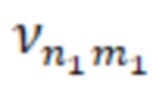 – корни производных функций Бесселя, соответствующих волнам ТЕ–типа с критической длиной волны равной
– корни производных функций Бесселя, соответствующих волнам ТЕ–типа с критической длиной волны равной 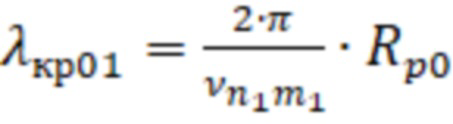 , для первой резонансной частоты;
, для первой резонансной частоты;
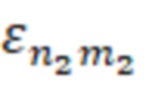 – корни функций Бесселя, соответствующие волнам ТН–типа с критической длиной волны равной
– корни функций Бесселя, соответствующие волнам ТН–типа с критической длиной волны равной 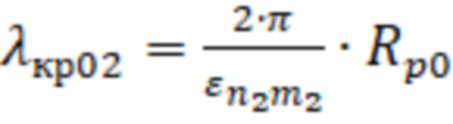 , или
, или 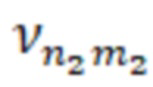 – корни производных функций Бесселя, соответствующих волнам ТЕ–типа с критической длиной волны равной
– корни производных функций Бесселя, соответствующих волнам ТЕ–типа с критической длиной волны равной 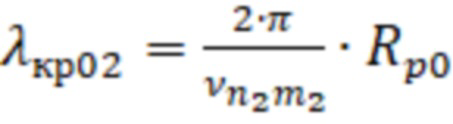 , для второй резонансной частоты;
, для второй резонансной частоты;
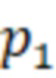 – число вариаций поля по длине резонатора, для первой резонансной частоты;
– число вариаций поля по длине резонатора, для первой резонансной частоты;
m1=0,1…M1 – число вариаций поля по радиусу, порядковый номер функции Бесселя, для первой резонансной частоты;
n1=1,2,…N1 – число вариаций поля по углу вдоль азимута, , для первой резонансной частоты;
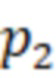 – число вариаций поля по длине резонатора, для второй резонансной частоты;
– число вариаций поля по длине резонатора, для второй резонансной частоты;
m2=0,1…M2 – число вариаций поля по радиусу, порядковый номер функции Бесселя, для первой резонансной частоты;
n2=1,2,…N2 – число вариаций поля по углу вдоль азимута, , для первой резонансной частоты;
с – скорость света;
 – константа;
– константа;
и определяют длину резонатора по формуле:
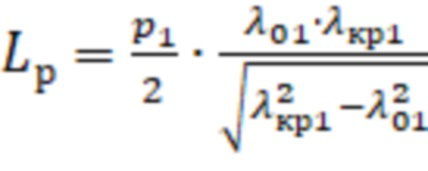 , (2)
, (2)
где 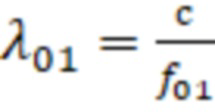 – длина волны на первой резонансной частоте;
– длина волны на первой резонансной частоте;
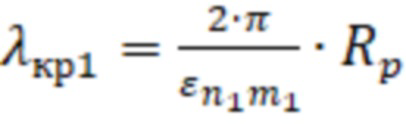 – критическая длина волны, соответствующая волнам ТН–типа или
– критическая длина волны, соответствующая волнам ТН–типа или 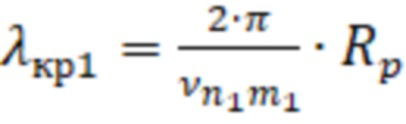 – критическая длина волны, соответствующая волнам ТЕ–типа, для первой резонансной частоты.
– критическая длина волны, соответствующая волнам ТЕ–типа, для первой резонансной частоты.
Для проверки процедуры определения геометрических параметров резонатора выбрали цилиндрический объемный резонатор для измерения относительной диэлектрической проницаемости ОР-2М радиусом примерно равным 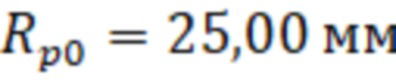 и приблизительной длиной
и приблизительной длиной 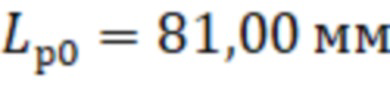 .
.
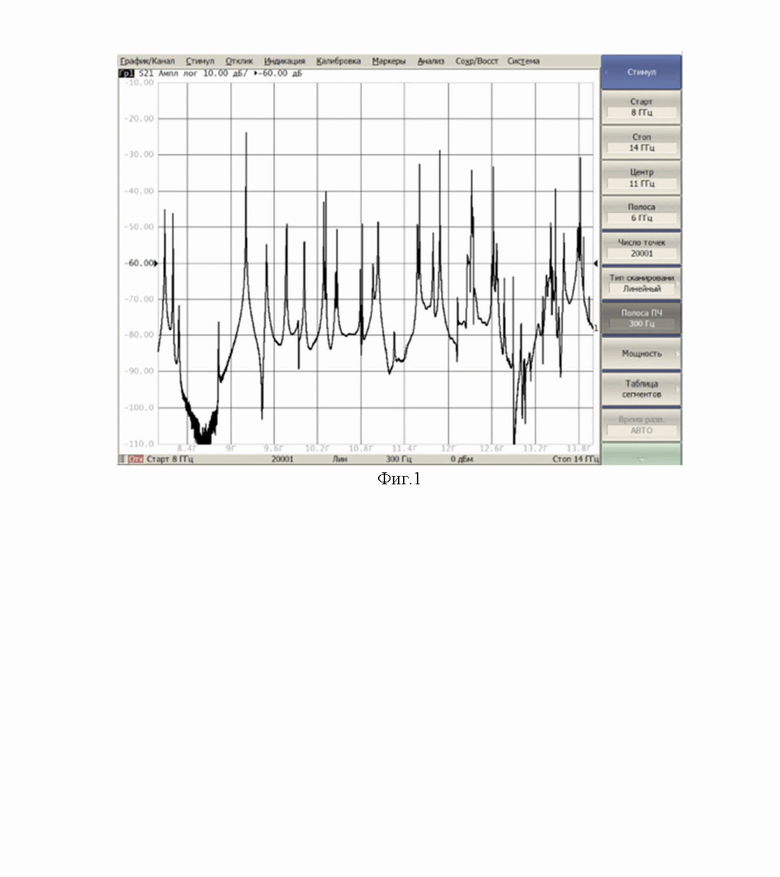
На фигуре 1 представлен частотный спектр амплитудного коэффициента передачи через резонатор (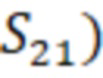 волноводного цилиндрического объемного резонатора ОР2-М, который измерялся с помощью векторного анализатора цепей S50244 с дискретностью 10 КГц в диапазоне от 8 до 14 ГГц. Из рассмотрения Фиг.1 видно, что определить по внешнему виду одинаковые типы волн для определения геометрических параметров полости резонатора не представляется возможным.
волноводного цилиндрического объемного резонатора ОР2-М, который измерялся с помощью векторного анализатора цепей S50244 с дискретностью 10 КГц в диапазоне от 8 до 14 ГГц. Из рассмотрения Фиг.1 видно, что определить по внешнему виду одинаковые типы волн для определения геометрических параметров полости резонатора не представляется возможным.
Таблица 1
Резонансные частоты, числа вариации полей и рассчитанные для них длины резонатора.
Путем расчетных процедур, используя данные в виде таблицы амплитуды коэффициента передачи резонатора от частоты 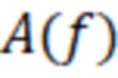 измеренной через 10 КГц, по максимумам амплитуды определяем резонансные частоты резонатора для различных типов волн.
измеренной через 10 КГц, по максимумам амплитуды определяем резонансные частоты резонатора для различных типов волн.
Список резонансных частот (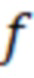 ) резонатора ОР2-М представлен в таблице 1, в которой также указаны числа вариаций поля по углу (n), радиусу (m) и длине (p) для типов волн, соответствующих резонансным частотам спектра амплитудного коэффициента передачи через резонатор, рассчитанным для приближенных значений геометрических размеров полости резонатора известных из априорных измерений радиусом равным
) резонатора ОР2-М представлен в таблице 1, в которой также указаны числа вариаций поля по углу (n), радиусу (m) и длине (p) для типов волн, соответствующих резонансным частотам спектра амплитудного коэффициента передачи через резонатор, рассчитанным для приближенных значений геометрических размеров полости резонатора известных из априорных измерений радиусом равным 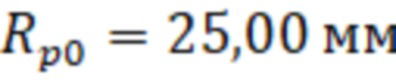 и длиной
и длиной 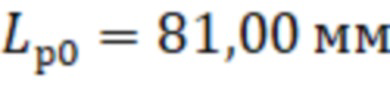 .
.
Таблица 2
Расчеты радиуса резонатора для различных пар частот.
Используя алгоритм, по предлагаемому техническому решению, проведены расчеты радиуса резонатора ОР2-М для различных пар частот из представленного спектра, которые представлены в таблице 2. Из таблицы
2 видно, что среднее из средне арифметических составляет 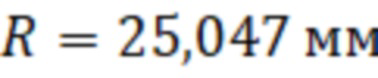 при этом максимальные отклонения составили от 0,22 мм до -0,297 мм, что говорит о необходимости более точного измерения частот в спектре резонатора, чем 10 КГц, но при этом очевидно, что использование пар частот с различными типами волн позволяет произвести определение радиуса резонатора используя метод стоячих волн, возбуждаемых в резонаторе.
при этом максимальные отклонения составили от 0,22 мм до -0,297 мм, что говорит о необходимости более точного измерения частот в спектре резонатора, чем 10 КГц, но при этом очевидно, что использование пар частот с различными типами волн позволяет произвести определение радиуса резонатора используя метод стоячих волн, возбуждаемых в резонаторе.
Используя алгоритм, по предлагаемому техническому решению, проведены расчеты длины резонатора ОР2-М для различных пар частот из представленного спектра с использованием данных о радиусе резонатора рассчитанных ранее, которые представлены в таблице 3. Из таблицы 3 видно, что среднее из средне арифметических составляет 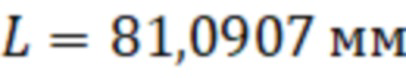 при этом максимальные отклонения составили от 0,691 мм до -0,850 мм, что, как и в предыдущем случае, говорит о необходимости более точного измерения частот в спектре резонатора, чем 10 КГц, но при этом очевидно, что использование пар частот с различными типами волн позволяет произвести определение длины резонатора используя метод стоячих волн, возбуждаемых в резонаторе.
при этом максимальные отклонения составили от 0,691 мм до -0,850 мм, что, как и в предыдущем случае, говорит о необходимости более точного измерения частот в спектре резонатора, чем 10 КГц, но при этом очевидно, что использование пар частот с различными типами волн позволяет произвести определение длины резонатора используя метод стоячих волн, возбуждаемых в резонаторе.
Таблица 3
Расчеты длины резонатора для различных пар частот.
Таким образом, установлено, что предложенный способ определения геометрических размеров цилиндрического резонатора позволяет повысить точность за счет процедуры определения с использованием резонансных частот из частотного спектра амплитудного коэффициента передачи через резонатор для различных типов волны и определения по ним геометрических размеров цилиндрического резонатора.
Изобретение относится к технике измерения параметров микроволновых линий, в частности к определению геометрических размеров цилиндрического резонатора. Предложен способ определения геометрических размеров цилиндрического резонатора, включающий измерение резонансных частот, возбуждаемых в резонаторе, и определение по резонансным частотам геометрических размеров резонатора, где измеряется частотный спектр амплитудного коэффициента передачи через резонатор резонансных частот, из которого определяют величины резонансных частот и их типы волн для приближенно известных размеров длины (Lp0) и радиуса (Rp0) резонатора. Техническим результатом при реализации заявленного решения является повышение точности определения геометрических параметров объемного цилиндрического резонатора за счет введения процедуры определения типов резонансных колебаний, возбуждаемых в резонаторе, и определения по ним геометрических размеров цилиндрического резонатора. 1 ил., 3 табл.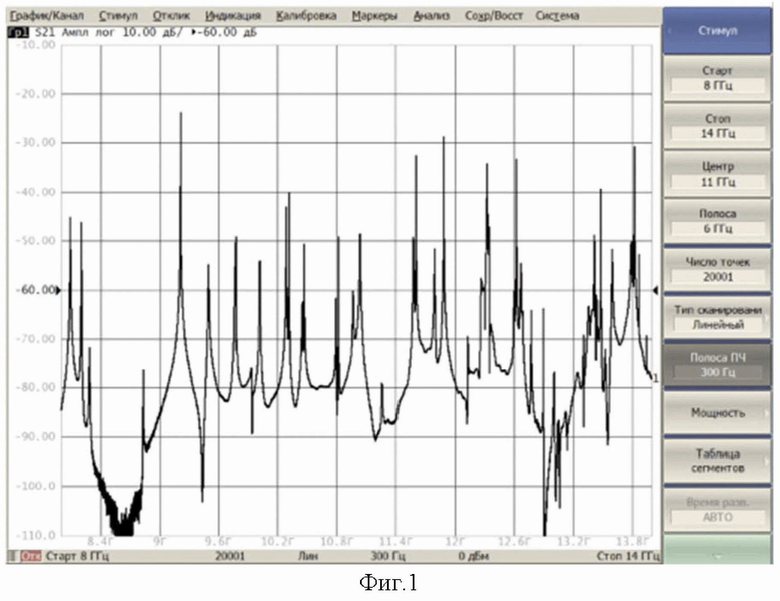
Способ определения геометрических размеров цилиндрического резонатора, включающий измерение резонансных частот, возбуждаемых в резонаторе, и определение по резонансным частотам геометрических размеров резонатора, отличающийся тем, что измеряется частотный спектр амплитудного коэффициента передачи через резонатор резонансных частот, из которого определяют величины резонансных частот и их типы волн для приближенно известных размеров длины (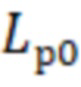 ) и радиуса (
) и радиуса (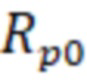 ) резонатора, затем выбирают любые две резонансные частоты, по которым определяют радиус резонатора по формуле
) резонатора, затем выбирают любые две резонансные частоты, по которым определяют радиус резонатора по формуле

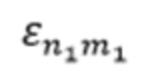 – корни функций Бесселя, соответствующие волнам ТН-типа с критической длиной волны, равной
– корни функций Бесселя, соответствующие волнам ТН-типа с критической длиной волны, равной 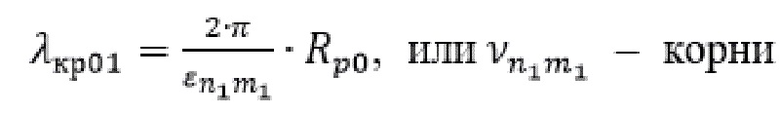 производных функций Бесселя, соответствующих волнам ТЕ-типа с критической длиной волны, равной
производных функций Бесселя, соответствующих волнам ТЕ-типа с критической длиной волны, равной 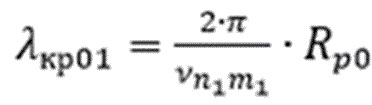 , для первой резонансной частоты;
, для первой резонансной частоты;
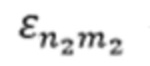 – корни функций Бесселя, соответствующие волнам ТН-типа с критической длиной волны, равной
– корни функций Бесселя, соответствующие волнам ТН-типа с критической длиной волны, равной 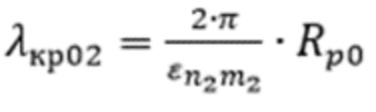 , или
, или 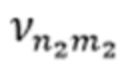 – корни производных функций Бесселя, соответствующих волнам ТЕ-типа с критической длиной волны, равной
– корни производных функций Бесселя, соответствующих волнам ТЕ-типа с критической длиной волны, равной 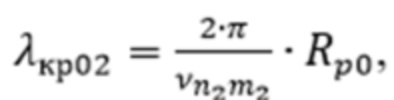 для второй резонансной частоты;
для второй резонансной частоты;
P1 – число вариаций поля по длине резонатора, для первой резонансной частоты;
m1=0, 1, …, M1 – число вариаций поля по радиусу, порядковый номер функции Бесселя, для первой резонансной частоты;
n1=1, 2, …, N1 – число вариаций поля по углу вдоль азимута, для первой резонансной частоты;
P2 – число вариаций поля по длине резонатора, для второй резонансной частоты;
m2=0, 1, …, M2 – число вариаций поля по радиусу, порядковый номер функции Бесселя, для первой резонансной частоты;
n2=1, 2, …, N2 – число вариаций поля по углу вдоль азимута, для первой резонансной частоты;
с – скорость света;
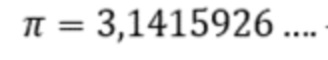 – константа;
– константа;
и определяют длину резонатора по формуле

где 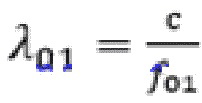 – длина волны на первой резонансной частоте;
– длина волны на первой резонансной частоте;
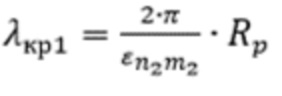 – критическая длина волны, соответствующая волнам ТН-типа, или
– критическая длина волны, соответствующая волнам ТН-типа, или 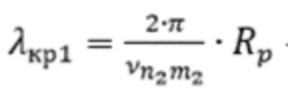 – критическая длина волны, соответствующая волнам ТЕ-типа, для первой резонансной частоты.
– критическая длина волны, соответствующая волнам ТЕ-типа, для первой резонансной частоты.
| Статья: "Измерение внутренних размеров сверхвысокочастотных объемных резонаторов", Ж | |||
| Измерительная техника | |||
| Способ восстановления спиралей из вольфрамовой проволоки для электрических ламп накаливания, наполненных газом | 1924 |
|
SU2020A1 |
| Разборное приспособление для накатки на рельсы сошедших с них колес подвижного состава | 1920 |
|
SU65A1 |
| Способ определения диэлектрической проницаемости | 1989 |
|
SU1707570A1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ГОДНОСТИ ЦИЛИНДРИЧЕСКИХ РЕЗОНАТОРОВ ЧАСТОТНЫХ ДАТЧИКОВ ДАВЛЕНИЯ | 2006 |
|
RU2315963C1 |
| Способ измерения резонансной частоты акустического резонатора газового термометра | 2017 |
|
RU2693539C2 |
| CN 100520421 C, 29.07.2009 | |||
| CN 1405569 A, 26.03.2003. | |||
Авторы
Даты
2024-04-05—Публикация
2023-06-20—Подача