Изобретение относится к области измерительной техники, а именно к приборам, используемым для вычисления магнитного курса в системах автономной ориентации и навигации подвижных объектов.
Из предшествующего уровня техники известно, что для измерения магнитного курса подвижного объекта используется информация с установленных на нем трех магнитометров и трех акселерометров, измерительные оси которых параллельны осям подвижного объекта. Ранее для решения данной задачи [патент RU 2629539, G01C 21/08, опубликован 29.06.2016] использовались сигналы, получаемые с трех магнитометров, трех акселерометров и двух датчиков угловой скорости, жестко закрепленных на подвижном объекте, оси которых параллельны связанным осям подвижного объекта. При этом для вычисления курса подвижного объекта вычисляют направляющие косинусы, по значениям которых вычисляют углы тангажа и крена. Используя полученные значения углов тангажа и крена, а также данные магнитометров, определяют магнитный курс, при этом в режиме равномерного движения указанные направляющие косинусы определяют непосредственно по данным акселерометров, в режиме с ускорением - по данным трех датчиков угловой скорости путем пошаговой коррекции матрицы направляющих косинусов связанных осей объекта относительно направлений на магнитные север и восток и местной вертикали на интервалах, в течение каждого из которых проекции вектора угловой скорости объекта могут считаться постоянными, при переходе объекта в режим движения с ускорением в качестве начального условия коррекции используют значение матрицы направляющих косинусов, вычисленное по углам магнитного курса, тангажа и крена на момент окончания режима равномерного движения.
Недостатками данного способа являются необходимость предварительного вычисления углов наклона (тангажа, крена) перед вычислением магнитного курса, что приводит к снижению точности вычисления магнитного курса подвижного объекта, а также невозможность обеспечения измерения углов магнитного курса в пределах полного оборота от нуля до трехсот шестидесяти градусов.
Известен способ измерения магнитного курса подвижного объекта [патент RU 2262075, G01C 21/12, 17/38, опубликован 10.10.2004], принятый в качестве прототипа, в котором используется информация о векторах магнитного поля Земли, линейного ускорения и как минимум двух проекциях вектора угловой скорости. Вычисление углов наклона, необходимых для определения магнитного курса, производится решением системы трех уравнений, два из которых представляют проекции вектора линейного ускорения на вертикаль места, а третье уравнение есть уравнение масштаба для направляющих косинусов, определяющих ориентацию вертикали места относительно связанной системы координат подвижного объекта. Для однозначного определения фактических углов наклона подвижного объекта определение истинного решения производится из условия равенства скорости изменения направляющего косинуса, полученного при решении системы уравнений, со скоростью изменения этого направляющего косинуса, вычисленной на основании информации о двух проекциях вектора угловой скорости подвижного объекта и двух направляющих косинусов.
Недостатками данного способа являются необходимость предварительного вычисления углов наклона (тангажа, крена) перед вычислением магнитного курса, что приводит к снижению точности вычисления магнитного курса подвижного объекта, а также невозможность обеспечения измерения углов магнитного курса в пределах полного оборота от нуля до трехсот шестидесяти градусов.
Принципиальное отличие заявленного способа измерения магнитного курса подвижного объекта от прототипа заключается в отсутствии необходимости предварительного вычисления углов наклона (тангажа, крена), что позволяет повысить точность, упростить алгоритм вычисления магнитного курса, а также обеспечить измерение углов магнитного курса подвижного объекта в пределах полного оборота - от нуля до трехсот шестидесяти градусов, что расширяет диапазон измерения.
Задача, на решение которой направлено заявленное изобретение, заключается в разработке способа измерения магнитного курса подвижного объекта по показаниям жестко закрепленных на подвижном объекте трех магнитометров, трех акселерометров и трех датчиков угловой скорости, оси которых параллельны связанным осям подвижного объекта, без необходимости предварительного вычисления углов наклона (тангажа, крена).
Технический результат - повышение точности вычисления магнитного курса подвижного объекта, а также расширение измерительного диапазона углов магнитного курса в пределах полного оборота от нуля до трехсот шестидесяти градусов.
Данный технический результат достигается за счет того, что в способе измерения магнитного курса подвижного объекта по показаниям трех магнитометров, трех акселерометров и трех датчиков угловой скорости, жестко закрепленных на подвижном объекте, оси которых параллельны связанным осям подвижного объекта, измеряемые с помощью акселерометров сигналы проекции линейного ускорения подвижного объекта и измеряемые с помощью датчиков угловой скорости сигналы проекции угловой скорости поступают на дискретный фильтр Винера, с помощью которого подавляют составляющие, вызванные равноускоренным движением подвижного объекта, и формируют оцененные значения линейного ускорения, далее полученные оцененные значения линейного ускорения нормируют по выражению:

где 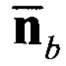 - нормированный вектор оцененного линейного ускорения подвижного объекта в связанной системе координат (ССК);
- нормированный вектор оцененного линейного ускорения подвижного объекта в связанной системе координат (ССК);
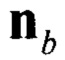 - вектор оцененного линейного ускорения подвижного объекта в ССК, сформированный по показаниям акселерометров и датчиков угловой скорости;
- вектор оцененного линейного ускорения подвижного объекта в ССК, сформированный по показаниям акселерометров и датчиков угловой скорости;
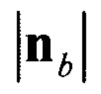 - норма сигнала вектора оцененного линейного ускорения подвижного объекта в ССК, аналогичным образом нормируют измеряемые с помощью магнитометров сигналы проекции вектора магнитного поля Земли, после чего по полученным нормированным сигналам при помощи условия выбора правильного решения, без необходимости предварительного вычисления углов тангажа и крена, вычисляют магнитный курс в диапазоне углов от нуля до трехсот шестидесяти градусов по зависимости:
- норма сигнала вектора оцененного линейного ускорения подвижного объекта в ССК, аналогичным образом нормируют измеряемые с помощью магнитометров сигналы проекции вектора магнитного поля Земли, после чего по полученным нормированным сигналам при помощи условия выбора правильного решения, без необходимости предварительного вычисления углов тангажа и крена, вычисляют магнитный курс в диапазоне углов от нуля до трехсот шестидесяти градусов по зависимости:
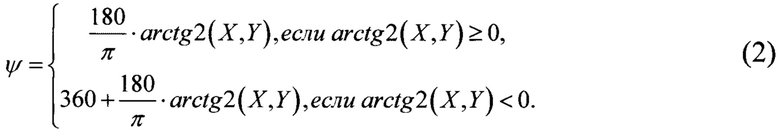
где 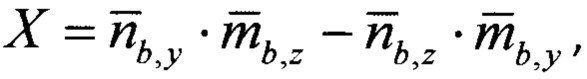
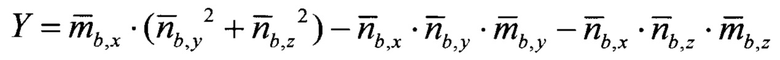
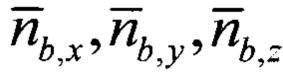 - нормированные проекции вектора оцененного линейного ускорения подвижного объекта на оси ССК, сформированные по показаниям акселерометров и датчиков угловой скорости;
- нормированные проекции вектора оцененного линейного ускорения подвижного объекта на оси ССК, сформированные по показаниям акселерометров и датчиков угловой скорости;
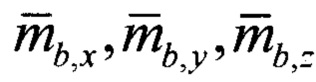 - нормированные проекции вектора напряженности магнитного поля Земли на оси ССК, измеренные с помощью магнитометров. Предлагаемый способ можно пояснить следующим образом. Измеряемые с помощью акселерометров сигналы проекции линейного ускорения
- нормированные проекции вектора напряженности магнитного поля Земли на оси ССК, измеренные с помощью магнитометров. Предлагаемый способ можно пояснить следующим образом. Измеряемые с помощью акселерометров сигналы проекции линейного ускорения 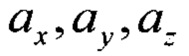 подвижного объекта и измеренные с помощью датчиков угловой скорости сигналы проекции угловой скорости
подвижного объекта и измеренные с помощью датчиков угловой скорости сигналы проекции угловой скорости 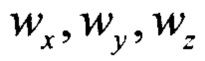 поступают на дискретный фильтр Винера.
поступают на дискретный фильтр Винера.
Дискретный фильтр Винера может быть реализован на основании известного способа [полезная модель RU 96235, G01C 21/16 опубликован 20.07.2010].
Дискретный фильтр Винера на основании кинематических выражений выделяет в наблюдаемых ускорениях проекции линейного ускорения подвижного объекта на оси связанной системы координат, а составляющие, обусловленные равноускоренным движением объекта, подавляет. Таким образом, после работы фильтра Винера получают оцененные сигналы о проекциях линейного ускорения, которые используют при вычислении магнитного курса подвижного объекта, работающего как в равномерном, так и равноускоренном режиме. Однако для вычисления магнитного курса необходимо привлекать информацию также об измерениях проекции вектора напряженности магнитного поля Земли (МПЗ). При этом можно использовать метод векторного согласования, заключающийся в определении взаимной ориентации связанной (с магнитометрами и оцененными сигналами о проекциях линейного ускорения, сформированными по показаниям акселерометров и датчиков угловой скорости) системы координат и опорного трехгранника по результатам измерений проекций не менее чем двух неколлинеарных векторов на оси обоих трехгранников [Кошелев, В. И. Использование фильтра Калмана с перекрестными связями в системе ориентации высокоманевренного объекта / В. И. Кошелев, В. А. Белокуров // Вестник Рязанского государственного радиотехнического университета. -2011. - №35. - С.3-7. - EDN NDTYKP]. В качестве опорного трехгранника рассматривается географическая система координат (ГСК) с центром в центре масс объекта [Челноков Ю.Н. Кватернионные и бикватернионные модели и методы механики твердого тела и их приложение. Геометрия и кинематика движения. - М.: ФИЗМАТЛИТ, 2006. - 512 с].
В ССК по показаниям жестко закрепленных на подвижном объекте трех магнитометров, трех акселерометров и трех датчиков угловой скорости, оси которых параллельны связанным осям подвижного объекта, можно сформировать два вектора:

где 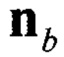 - вектор оцененного линейного ускорения подвижного объекта в ССК, сформированный по показаниям акселерометров и датчиков угловой скорости (сигналы на выходе фильтра Винера);
- вектор оцененного линейного ускорения подвижного объекта в ССК, сформированный по показаниям акселерометров и датчиков угловой скорости (сигналы на выходе фильтра Винера);
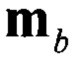 - вектор напряженности магнитного поля Земли в ССК, сформированный с помощью показаний магнитометров.
- вектор напряженности магнитного поля Земли в ССК, сформированный с помощью показаний магнитометров.
Данные векторы проходят процедуру нормирования, под которой понимают нахождение единичного вектора для заданного вектора. Процедуру нормирования осуществляют, используя выражение (1) для оцененного линейного ускорения подвижного объекта и аналогично для напряженности МПЗ в соответствии:

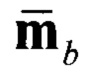 - нормированный вектор напряженности магнитного поля Земли в ССК, сформированный с помощью показаний магнитометров;
- нормированный вектор напряженности магнитного поля Земли в ССК, сформированный с помощью показаний магнитометров;
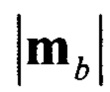 - норма сигнала напряженности магнитного поля Земли в ССК.
- норма сигнала напряженности магнитного поля Земли в ССК.
Вычисление нормы сигнала вектора линейного ускорения подвижного объекта и напряженности магнитного поля Земли в ССК на основании данных, сформированных с помощью оцененных сигналов проекции линейного ускорения и сигналов магнитометров, должно осуществляться следующим образом:
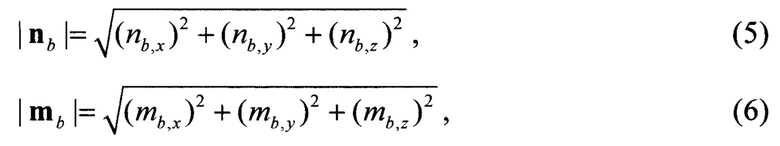
где 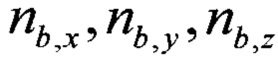 - проекции вектора оцененного линейного ускорения подвижного объекта на оси ССК, сформированные по показаниям акселерометров и датчиков угловой скорости;
- проекции вектора оцененного линейного ускорения подвижного объекта на оси ССК, сформированные по показаниям акселерометров и датчиков угловой скорости;
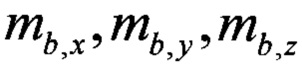 - проекции вектора напряженности магнитного поля Земли на оси ССК, измеренные с помощью магнитометров.
- проекции вектора напряженности магнитного поля Земли на оси ССК, измеренные с помощью магнитометров.
Также в неподвижной географической системе координат (ГСК) по априорно известной информации о значениях линейного ускорения (действующего ускорения свободного падения Земли) и напряженности магнитного поля Земли в произвольной точке местности можно сформировать два вектора:
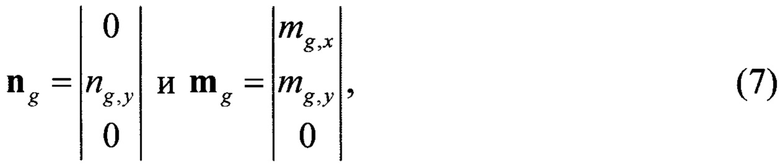
где 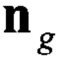 - вектор линейного ускорения подвижного объекта в ГСК;
- вектор линейного ускорения подвижного объекта в ГСК;
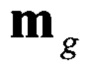 - вектор напряженности магнитного поля Земли в ГСК;
- вектор напряженности магнитного поля Земли в ГСК;
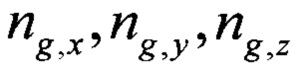 - проекции вектора линейного ускорения подвижного объекта на оси ГСК;
- проекции вектора линейного ускорения подвижного объекта на оси ГСК;
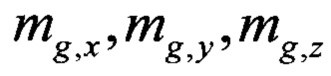 - проекции вектора напряженности магнитного поля Земли на оси ГСК.
- проекции вектора напряженности магнитного поля Земли на оси ГСК.
Данные векторы проходят процедуру нормирования, под которой понимают нахождение единичного вектора для заданного вектора. Аналогичным образом нормируют показания векторов в ГСК.

где 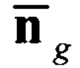 - нормированный вектор линейного ускорения подвижного объекта в ГСК;
- нормированный вектор линейного ускорения подвижного объекта в ГСК;
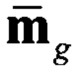 - нормированный вектор напряженности магнитного поля Земли в ГСК;
- нормированный вектор напряженности магнитного поля Земли в ГСК;
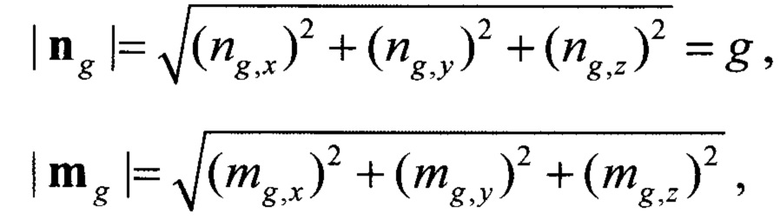
где 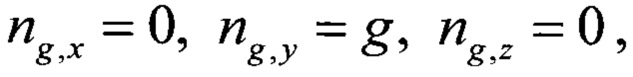 g - ускорение свободного падения Земли в рассматриваемой точке местности.
g - ускорение свободного падения Земли в рассматриваемой точке местности.
Для реализации векторного согласования найдем такую ортогональную матрицу 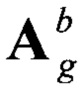 , которая бы удовлетворяла условиям:
, которая бы удовлетворяла условиям:
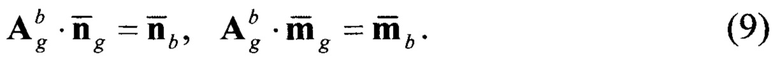
На основании (9) можно получить два ортонормированных базиса:
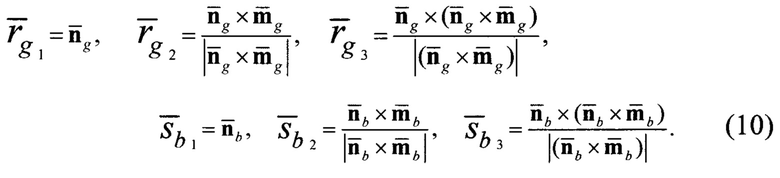
где 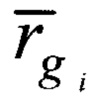 - векторы, составляющие ортонормированный базис в ГСК;
- векторы, составляющие ортонормированный базис в ГСК;
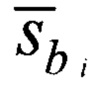 - векторы, составляющие ортонормированный базис в ССК;
- векторы, составляющие ортонормированный базис в ССК;
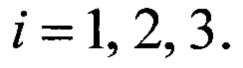
Тогда будет существовать такая единичная ортогональная матрица 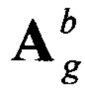 , которая будет удовлетворять выполнению следующего равенства:
, которая будет удовлетворять выполнению следующего равенства:

Решение матрицы 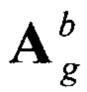 , описывающей переход из ГСК в ССК, будет иметь вид:
, описывающей переход из ГСК в ССК, будет иметь вид:
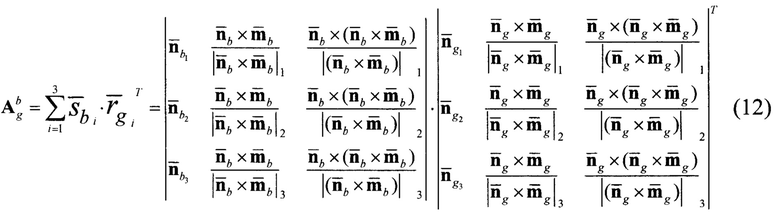
Вследствие того, что показания векторов 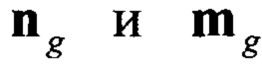 в ГСК после проведения операции нормирования, в соответствии с (1) и (4), принимают вид:
в ГСК после проведения операции нормирования, в соответствии с (1) и (4), принимают вид:
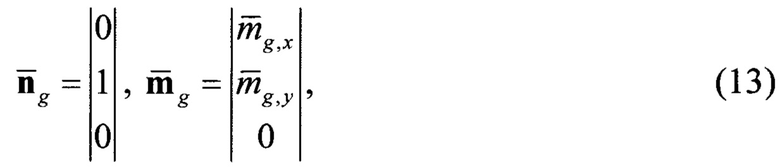
где 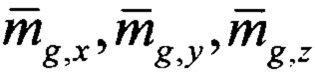 - нормированные проекции вектора напряженности магнитного поля Земли на оси ГСК в рассматриваемой точке местности, то:
- нормированные проекции вектора напряженности магнитного поля Земли на оси ГСК в рассматриваемой точке местности, то:
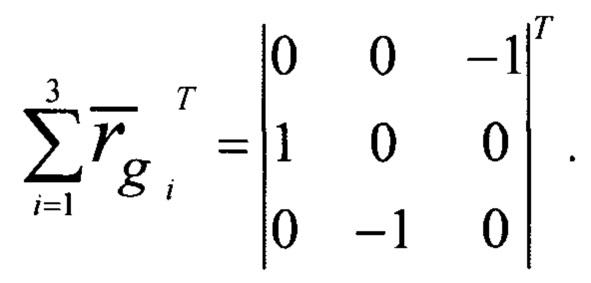
Тогда, упрощая выражение (12), получим матрицу 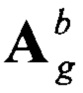 вида:
вида:
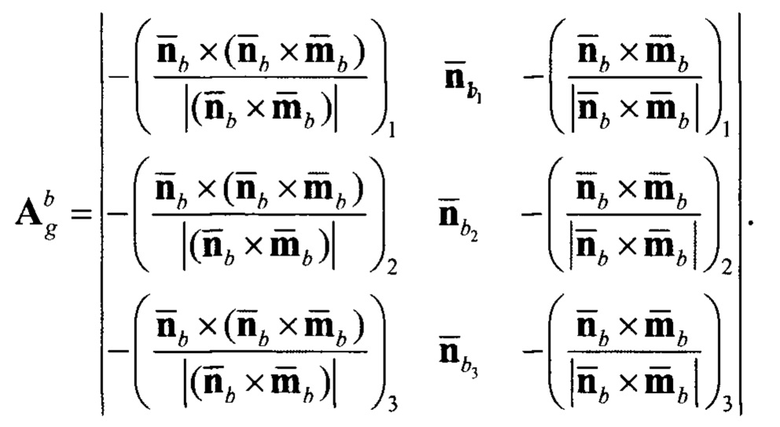
Вычисление магнитного курса подвижного объекта осуществляется по элементам матрицы в соответствии с выражением:
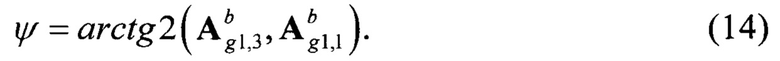
Раскрывая выражение (13), получим новое выражение для вычисления магнитного курса по нормированным сигналам оцененных проекций линейного ускорения 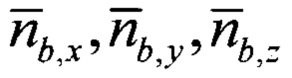 (сформированным по показаниям акселерометров и датчиков угловой скорости) и измеренным с помощью магнитометров нормированным сигналам проекции вектора магнитного поля Земли
(сформированным по показаниям акселерометров и датчиков угловой скорости) и измеренным с помощью магнитометров нормированным сигналам проекции вектора магнитного поля Земли 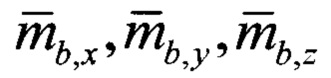 (по показаниям магнитометров), которое не требует предварительного определения углов тангажа и крена подвижного объекта:
(по показаниям магнитометров), которое не требует предварительного определения углов тангажа и крена подвижного объекта:

где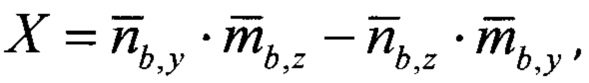
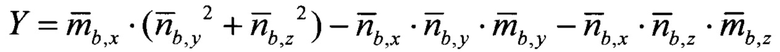
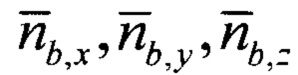 - нормированные проекции вектора линейного ускорения подвижного объекта на оси ССК, сформированные по показаниям акселерометров и датчиков угловой скорости;
- нормированные проекции вектора линейного ускорения подвижного объекта на оси ССК, сформированные по показаниям акселерометров и датчиков угловой скорости;
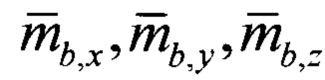 - нормированные проекции вектора напряженности магнитного поля Земли на оси ССК, измеренные с помощью магнитометров.
- нормированные проекции вектора напряженности магнитного поля Земли на оси ССК, измеренные с помощью магнитометров.
Для измерения углов магнитного курса в пределах полного оборота от нуля до трехсот шестидесяти градусов необходимо обеспечить проверку условия выбора в выражении (15). После чего измерение магнитного курса подвижного объекта осуществляется без необходимости предварительного вычисления углов тангажа и крена, в диапазоне углов от нуля до трехсот шестидесяти градусов по зависимости (2).
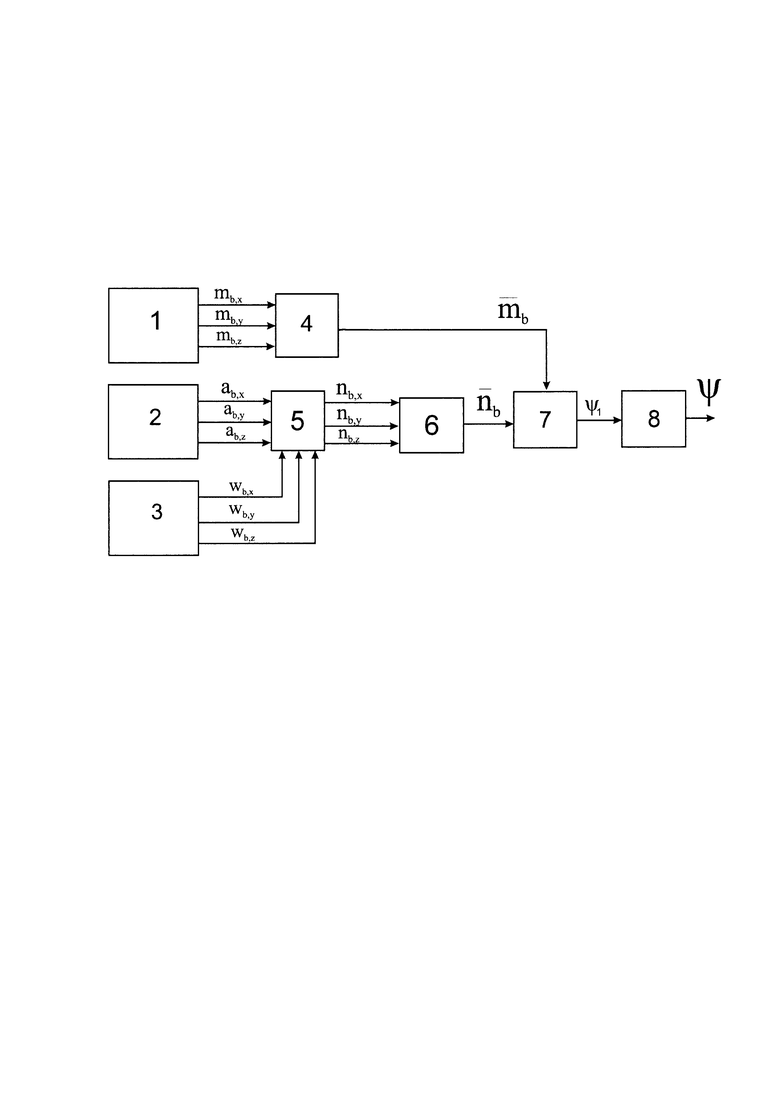
На чертеже представлен алгоритм работы заявленного способа.
Блок магнитометров 1, блок акселерометров 2 и блок датчиков угловой скорости 3 жестко закреплены на подвижном объекте и их измерительные оси ортогональны осям подвижного объекта, соответственно осям ОХ, ОУ и OZ, начала которых находятся в центре масс подвижного объекта. Выходы блока магнитометров 1 соединены с входами блока нормирования магнитометров 4. Выходы блока акселерометров 2 и блока датчиков угловой скорости 3 соединены с соответствующими входами блока дискретного фильтра Винера 5. Выходы блока дискретного фильтра Винера 5 соединены с входами нормирования оцененных линейных ускорений 6. Выходы нормирования магнитометров 4 и нормирования оцененных линейных ускорений 6 соединены с входами блока проверки условия 7. Выход блока проверки условия 7 соединен с входом блока вычисления магнитного курса 8. Выход блока 8 выдает информацию потребителю.
Способ реализуют следующим образом.
Сигналы с блока магнитометров 1, измеряющего три компоненты вектора 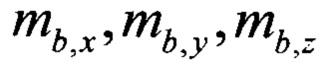 напряженности магнитного поля Земли в ССК, поступают на входы блока нормирования магнитометров 4. В блоке 4 реализуют решение уравнения (4) на каждом шаге измеряемых значений. Сигналы с блока акселерометров 2, измеряющего три компоненты вектора
напряженности магнитного поля Земли в ССК, поступают на входы блока нормирования магнитометров 4. В блоке 4 реализуют решение уравнения (4) на каждом шаге измеряемых значений. Сигналы с блока акселерометров 2, измеряющего три компоненты вектора 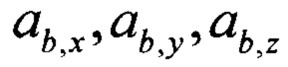 линейного ускорения подвижного объекта в ССК, и сигналы с блока датчиков угловой скорости 3, измеряющего три компоненты вектора
линейного ускорения подвижного объекта в ССК, и сигналы с блока датчиков угловой скорости 3, измеряющего три компоненты вектора 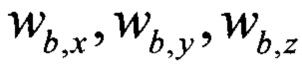 угловой скорости, поступают на входы дискретного фильтра Винера 5. В блоке дискретного фильтра Винера 5 на основании кинематических выражений выделяются в наблюдаемых ускорениях проекции оцененного линейного ускорения подвижного объекта на оси связанной системы координат, а составляющие, обусловленные равноускоренным движением объекта, подавляются. На выходах дискретного фильтра Винера 5 получают оцененные сигналы о проекциях линейного ускорения
угловой скорости, поступают на входы дискретного фильтра Винера 5. В блоке дискретного фильтра Винера 5 на основании кинематических выражений выделяются в наблюдаемых ускорениях проекции оцененного линейного ускорения подвижного объекта на оси связанной системы координат, а составляющие, обусловленные равноускоренным движением объекта, подавляются. На выходах дискретного фильтра Винера 5 получают оцененные сигналы о проекциях линейного ускорения 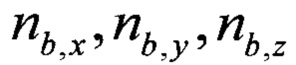 , которые поступают на входы блока нормирования оцененных линейных ускорений 6. В блоке нормирования оцененных линейных ускорений 6 реализуется уравнение (1). Сигнал с выхода блока нормирования магнитометров 4 и сигнал с выхода блока нормирования оцененных линейных ускорений 6 поступают на входы блока проверки условия 7, в котором реализуется проверка выражения (15). Сигнал с выхода блока проверки условия 7 поступает на вход блока вычисления магнитного курса 8, реализующего решение в соответствии с выражением (2), обеспечивая измерение магнитного курса подвижного объекта в пределах полного оборота от нуля до трехсот шестидесяти градусов.
, которые поступают на входы блока нормирования оцененных линейных ускорений 6. В блоке нормирования оцененных линейных ускорений 6 реализуется уравнение (1). Сигнал с выхода блока нормирования магнитометров 4 и сигнал с выхода блока нормирования оцененных линейных ускорений 6 поступают на входы блока проверки условия 7, в котором реализуется проверка выражения (15). Сигнал с выхода блока проверки условия 7 поступает на вход блока вычисления магнитного курса 8, реализующего решение в соответствии с выражением (2), обеспечивая измерение магнитного курса подвижного объекта в пределах полного оборота от нуля до трехсот шестидесяти градусов.
Таким образом, заявленный способ измерения магнитного курса подвижного объекта позволяет повысить точность вычисления магнитного курса подвижного объекта и расширить диапазон измерения в пределах полного оборота от нуля до трехсот шестидесяти градусов.
| название | год | авторы | номер документа |
|---|---|---|---|
| Электронный компас для подвижного объекта | 2024 |
|
RU2829808C1 |
| Способ оценки пространственного и углового положения объекта | 2024 |
|
RU2831368C1 |
| Способ коррекции бесплатформенной инерциальной навигационной системы | 2016 |
|
RU2635820C1 |
| Бесплатформенная инерциальная курсовертикаль | 2016 |
|
RU2643201C2 |
| СПОСОБ ИЗМЕРЕНИЯ МАГНИТНОГО КУРСА ПОДВИЖНОГО ОБЪЕКТА | 2016 |
|
RU2629539C1 |
| Способы формирования данных об ориентации объекта и навигационный комплекс летательного аппарата для их реализации | 2020 |
|
RU2745083C1 |
| СПОСОБ ИЗМЕРЕНИЯ МАГНИТНОГО КУРСА ПОДВИЖНОГО ОБЪЕКТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2262075C1 |
| СПОСОБ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ И ЕЁ КОРРЕКЦИИ ПО НЕПОДВИЖНОМУ НАЗЕМНОМУ ОРИЕНТИРУ С ИЗВЕСТНЫМИ ГЕОГРАФИЧЕСКИМИ КООРДИНАТАМИ | 2019 |
|
RU2713582C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ УГЛОВ ПРОСТРАНСТВЕННОЙ ОРИЕНТАЦИИ ПОДВИЖНОГО ОБЪЕКТА | 2014 |
|
RU2555496C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИСТИННОГО КУРСА ПОДВИЖНОГО ОБЪЕКТА | 2017 |
|
RU2671937C1 |
Изобретение относится к измерительной технике, а именно к приборам для вычисления магнитного курса в системах автономной ориентации и навигации подвижных объектов (ПО). Сущность заявленного способа заключается в том, что измеряемые с помощью акселерометров сигналы проекции линейного ускорения ПО и измеренные с помощью датчиков угловой скорости сигналы проекции угловой скорости поступают на дискретный фильтр Винера, с помощью которого подавляют составляющие, вызванные равноускоренным движением ПО, и формируют оцененные значения линейного ускорения, далее полученные оцененные значения линейного ускорения и измеряемые с помощью магнитометров сигналы проекции вектора магнитного поля Земли нормируют, после чего по полученным нормированным сигналам определяют магнитный курс ПО в диапазоне углов от нуля до трехсот шестидесяти градусов. Технический результат заявленного решения заключается в повышении точности вычисления магнитного курса ПО и расширении диапазона измерения. 1 ил.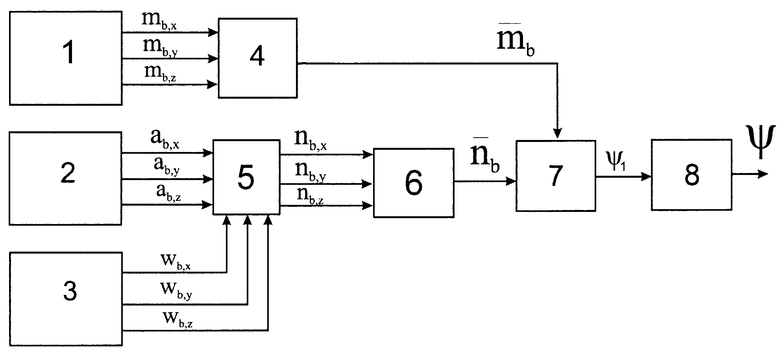
Способ измерения магнитного курса подвижного объекта по показаниям трех магнитометров, трех акселерометров и трех датчиков угловой скорости, жестко закрепленных на подвижном объекте, оси которых параллельны связанным осям подвижного объекта, отличающийся тем, что измеряемые с помощью акселерометров сигналы проекции линейного ускорения подвижного объекта и измеряемые с помощью датчиков угловой скорости сигналы проекции угловой скорости поступают на дискретный фильтр Винера, с помощью которого подавляют составляющие, вызванные равноускоренным движением подвижного объекта, и формируют оцененные значения линейного ускорения, далее полученные оцененные значения линейного ускорения нормируют по выражению
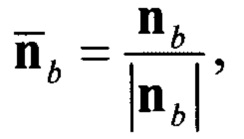
где 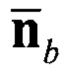 - нормированный вектор оцененного линейного ускорения подвижного объекта в связанной системе координат;
- нормированный вектор оцененного линейного ускорения подвижного объекта в связанной системе координат;
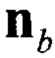 - вектор оцененного линейного ускорения подвижного объекта в связанной системе координат, сформированный по показаниям акселерометров и датчиков угловой скорости;
- вектор оцененного линейного ускорения подвижного объекта в связанной системе координат, сформированный по показаниям акселерометров и датчиков угловой скорости;
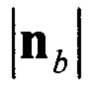 - норма вектора оцененного линейного ускорения подвижного объекта в связанной системе координат,
- норма вектора оцененного линейного ускорения подвижного объекта в связанной системе координат,
аналогичным образом нормируют измеряемые с помощью магнитометров сигналы проекции вектора магнитного поля Земли, после чего по полученным нормированным сигналам при выполнении условия  определяют магнитный курс подвижного объекта в диапазоне углов от нуля до трехсот шестидесяти градусов по зависимости:
определяют магнитный курс подвижного объекта в диапазоне углов от нуля до трехсот шестидесяти градусов по зависимости:
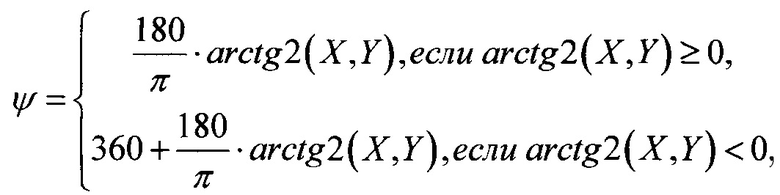
где 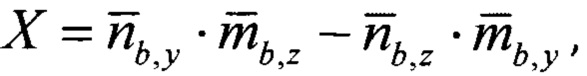
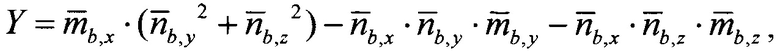
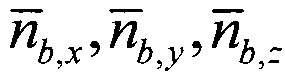 - нормированные проекции вектора оцененного линейного ускорения подвижного объекта на оси связанной системы координат, сформированные по показаниям акселерометров и датчиков угловой скорости;
- нормированные проекции вектора оцененного линейного ускорения подвижного объекта на оси связанной системы координат, сформированные по показаниям акселерометров и датчиков угловой скорости;
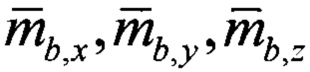 - нормированные проекции вектора напряженности магнитного поля Земли на оси связанной системы координат, измеренные с помощью магнитометров.
- нормированные проекции вектора напряженности магнитного поля Земли на оси связанной системы координат, измеренные с помощью магнитометров.
| СПОСОБ ИЗМЕРЕНИЯ МАГНИТНОГО КУРСА ПОДВИЖНОГО ОБЪЕКТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2262075C1 |
| СПОСОБ ИЗМЕРЕНИЯ МАГНИТНОГО КУРСА ПОДВИЖНОГО ОБЪЕКТА | 2016 |
|
RU2629539C1 |
| СПОСОБ КАЛИБРОВКИ ЭЛЕКТРОННОГО МАГНИТНОГО КОМПАСА | 2014 |
|
RU2572109C1 |
| US 0006651003 B2, 18.11.2003. | |||
Авторы
Даты
2024-12-02—Публикация
2024-06-06—Подача