Изобретение относится к области измерительных информационных систем и комплексов боевых самолетов и вертолетов, в котором приведена разработка унифицированного способа оптимального оценивания полного перечня параметров состояния инерциальной навигационной системы (ИНС) и эффективной коррекции измеряемой ей навигационной и пилотажной информации.
Известен способ определения текущих ошибок счисления географических координат местоположения летательного аппарата (ЛА) и их коррекции по результатам аппаратного углового сопровождения наземного ориентира коррекции (ОК) с известными географическими координатами с измерением при этом текущих углов его относительной ориентации и наклонной дальности до него.
Указанный способ представлен в монографии О.А. Бабича «Обработка информации в навигационных комплексах», М., «Машиностроение», 1991 [1] (подраздел 3.4.1, стр. 225-229).
Рассмотрение его сути целесообразно начать с решения так называемой прямой задачи и после представления используемых при ее решении параметров, математических преобразований и расчетных соотношений, перейти к рассмотрению обратной задачи, в которой и раскрывается суть способа, который предлагается использовать в качестве наиболее близкого аналога предлагаемого алгоритмического решения.
Суть прямой задачи ([1], стр. 226) достаточно тривиальна и заключается в определении текущих значений дальности, азимута и угла места направления на ориентир коррекции с известными географическими координатами. При этом предполагается, что текущие, счисленные ИНС, географические координаты местоположения объекта известны.
При ее решении используется известная в теории навигации, наведения и управления процедура гринвичских координат, заключающаяся в преобразовании географических координат текущего местоположения объекта и ориентира коррекции в линейные прямоугольные координаты в проекциях на оси гринвичской системы координат.
В обозначениях, принятых ниже для географических координат текущего местоположения объекта ϕ, λ, h и ориентира коррекции ϕ0, λ0, h0, выражения для расчета гринвичских координат объекта X', Y', Z' и ОК 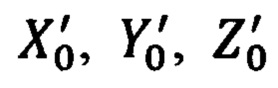 будут иметь следующий вид:
будут иметь следующий вид:
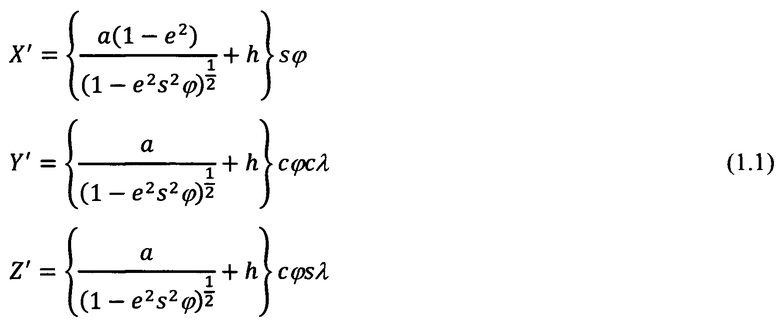
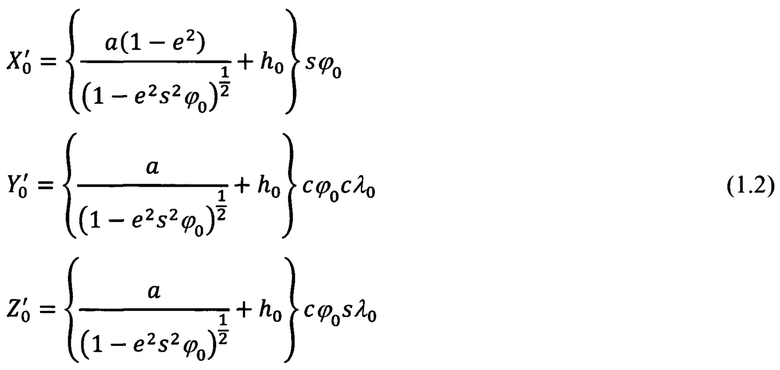
Здесь и далее под «с» следует понимать косинус, а под «s» - синус соответствующего угла.
Вся необходимая информация об используемых в (1.1) и (1.2) параметрах Земли а, е2 представлена ниже.
Процедура расчета искомых координат (дальности, азимута, угла места) относительной ориентации ориентира коррекции предполагает предварительное приведение относительных гринвичских координат местоположения ОК к осям географического сопровождающего трехгранника (ГСТ) ONHE объекта (стр. 226 [1]).
Приведем полную сводку выражений для расчета упомянутых дальности ΔD0, азимута А0 и угла места θ0 относительной ориентации ОК:
- расчет прямоугольных гринвичских координат относительной ориентации ОК:

- приведение компонент 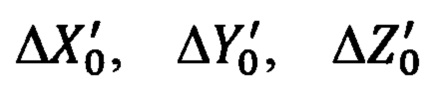 к осям географического сопровождающего трехгранника ГСТ ONHE объекта осуществляется в соответствии с векторно-матричным выражением (3), в котором используется матрица (5):
к осям географического сопровождающего трехгранника ГСТ ONHE объекта осуществляется в соответствии с векторно-матричным выражением (3), в котором используется матрица (5):
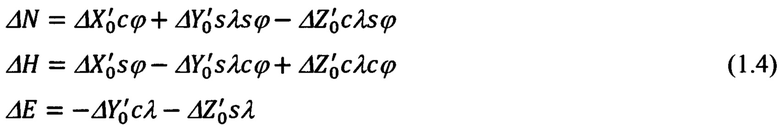
Приведенные выражения справедливы для взаимной ориентации ГСТ ONHE и гринвичской системы координат ГСК OX'Y'Z', представленной на фиг. 1, 2.
- расчет относительной дальности ΔD0, азимута А0 и угла места θ0 ОК:
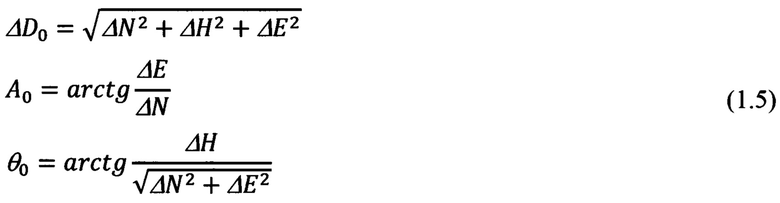
В обратной задаче по измеренным обзорно-прицельной системой (ОПС) текущим значениям углов ϕy, ϕz визирования ОК и наклонной дальности 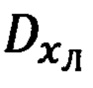 до него, определяют текущие значения компонент Dx, Dy, Dz указанной дальности в проекциях на оси связанной с объектом системы координат (ССК) Oxyz. После чего, используя текущие значения истинного курса ψи, крена γ и тангажа υ объекта, указанные составляющие дальности приводят к осям ГСТ ONHE объекта и находят тем самым компоненты дальности DN, DH, DE. Их аналог представлен 1-ой строкой системы (3.91) [1]. Используя указанные составляющие дальности DN, DH, DE и относительные координаты текущего местоположения ОК
до него, определяют текущие значения компонент Dx, Dy, Dz указанной дальности в проекциях на оси связанной с объектом системы координат (ССК) Oxyz. После чего, используя текущие значения истинного курса ψи, крена γ и тангажа υ объекта, указанные составляющие дальности приводят к осям ГСТ ONHE объекта и находят тем самым компоненты дальности DN, DH, DE. Их аналог представлен 1-ой строкой системы (3.91) [1]. Используя указанные составляющие дальности DN, DH, DE и относительные координаты текущего местоположения ОК 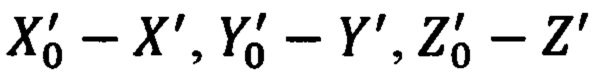 в проекциях на оси гринвичской системы координат (ГСК) (1.3), формируют некие уравнения, связывающие гринвичские координаты текущего местоположения объекта X', Y', Z' (ϕ, λ, h) и компоненты дальности DN, DH, DE. Аналог указанных уравнений связи представлен на стр. 227 [1].
в проекциях на оси гринвичской системы координат (ГСК) (1.3), формируют некие уравнения, связывающие гринвичские координаты текущего местоположения объекта X', Y', Z' (ϕ, λ, h) и компоненты дальности DN, DH, DE. Аналог указанных уравнений связи представлен на стр. 227 [1].
Формализуя представленное выше описание процедуры решения обратной задачи, приведем полный перечень математических операций и реализующих их выражений, в соответствии с которыми формируют упомянутые выше уравнения связи:
- расчет компонент Dx, Dy, Dz дальности до ориентира коррекции по измерениям ОПС в проекциях на оси ССК Oxyz - осуществляется в соответствии с фиг. 5 и векторно-матричным выражением (16), в котором используется матрица LT вида(18):

Пересчет полученных по измерениям ОПС компонент Dx, Dy, Dz (1.6) дальности на оси ГСТ ONHE объекта осуществляется в соответствии с фиг. 6 и векторно-матричным выражением (27) с используемой в нем матрицей 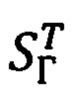 (29):
(29):
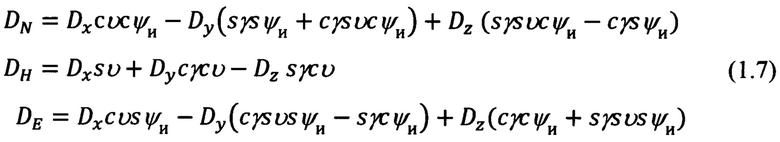
В наиболее близком аналоге приведенные выше математические процедуры (1.6) и (1.7) по расчету компонент дальности Dx, Dy, Dz и DN, DH, DE сведены в одну, которая обеспечивает непосредственный расчет компонент DN, DH, DE по измеренной наклонной дальности 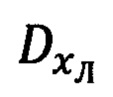 до ОК и сформированным неким комбинированным устройством, совмещающим в себе оптический визир и курсовертикаль, текущим значениям углов азимута и угла места на ОК.
до ОК и сформированным неким комбинированным устройством, совмещающим в себе оптический визир и курсовертикаль, текущим значениям углов азимута и угла места на ОК.
Опыт эксплуатации прицельных систем свидетельствует о том, что подобных комбинированных устройств не существует, тем более с абсолютно безошибочным измерением азимута и угла места.
Поэтому ниже это обстоятельство будет расценено, как один из недостатков прототипа.
Для формирования математически строгих уравнений связи необходимо компоненты DN, DH, DE дальности (1.7), полученные по измерениям ОПС, привести к осям ГСК OX'Y'Z' и сравнить с аналогичными компонентами 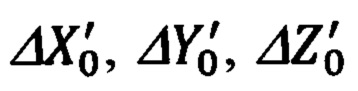 (1.3) дальности, сформированными по результатам навигационных измерений (1.1), (1.2). Приведение составляющих DN, DH, DE дальности до ОК (1.7) к осям ГСК OX'Y'Z' осуществляют в соответствии с векторно-матричным выражением (4).
(1.3) дальности, сформированными по результатам навигационных измерений (1.1), (1.2). Приведение составляющих DN, DH, DE дальности до ОК (1.7) к осям ГСК OX'Y'Z' осуществляют в соответствии с векторно-матричным выражением (4).
В скалярном виде выражения для компонент дальности (1.7) в проекциях на оси ГСК OX'Y'Z', в соответствии с (4) и (6), будут иметь вид:
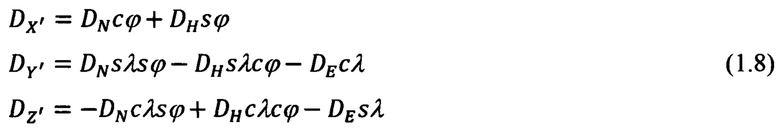
Сравнение (1.3) с (1.8) приводит к следующим уравнениям связи:
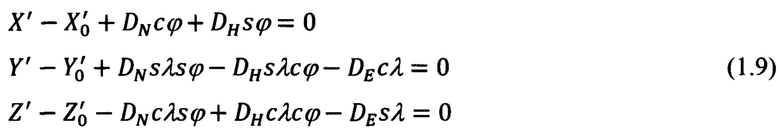
Учитывая, что как географические координаты ϕ0, λ0, h0 ОК, так и полученные на их основе гринвичские координаты 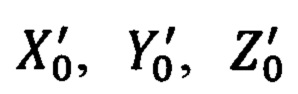 (1.2) известны абсолютно точно, а ошибочными являются счисленные ИНС значения географических координат
(1.2) известны абсолютно точно, а ошибочными являются счисленные ИНС значения географических координат 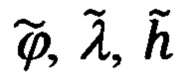 текущего местоположения объекта и адекватные им по точности линейные гринвичские координаты
текущего местоположения объекта и адекватные им по точности линейные гринвичские координаты 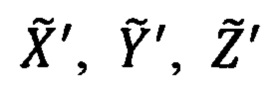 (1.1) - полученные уравнения связи (1.9) правомочно трактовать, как уравнения, связывающие ошибки Δϕ, Δλ, Δh счисления географических координат
(1.1) - полученные уравнения связи (1.9) правомочно трактовать, как уравнения, связывающие ошибки Δϕ, Δλ, Δh счисления географических координат 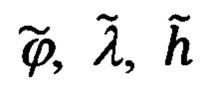 и соответствующие им ошибки ΔХ', ΔY', ΔZ' определения гринвичских координат
и соответствующие им ошибки ΔХ', ΔY', ΔZ' определения гринвичских координат 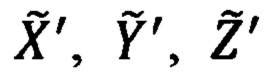 текущего местоположения объекта.
текущего местоположения объекта.
Действительно, если в полученных уравнениях связи (1.9) положить, что идеальные значения координат ϕ, λ, h и X', Y', Z' текущего местоположения объекта определяются соотношениями вида:

где 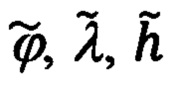 - счисленные ИНС значения географических координат местоположения объекта;
- счисленные ИНС значения географических координат местоположения объекта;  - полученные на их основе гринвичские координаты; Δϕ, Δλ, Δh, ΔХ', ΔY', ΔZ' - соответствующие ошибки счисления, подлежащие определению, то полученные таким образом уравнения связи будут иметь представленную выше трактовку.
- полученные на их основе гринвичские координаты; Δϕ, Δλ, Δh, ΔХ', ΔY', ΔZ' - соответствующие ошибки счисления, подлежащие определению, то полученные таким образом уравнения связи будут иметь представленную выше трактовку.
Действительно, в соответствии с фигурой земного эллипсоида вращения, достаточно просто можно получить выражения, связывающие вариации линейных гринвичских координат ΔХ', ΔY', ΔZ' с линейными вариациями 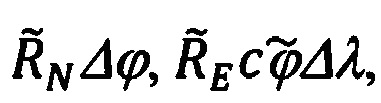 Δh в проекциях на оси ГСТ ONHE объекта.
Δh в проекциях на оси ГСТ ONHE объекта.
Запишем их в виде следующего векторно-матричного выражения:

где 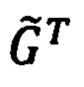 - представленная ниже ортогональная матрица (6), определяемая текущими значениями счисленных географических координат
- представленная ниже ортогональная матрица (6), определяемая текущими значениями счисленных географических координат 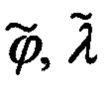 местоположения объекта.
местоположения объекта.
Подставляя (2) в (1.10) и далее в уравнения связи вида (1.9) с учетом трех последних соотношений системы (1.10), получают систему из трех алгебраических уравнений относительно 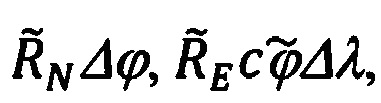 и Δh.
и Δh.
Ее решение позволяет определить текущие ошибки счисления Δϕ, Δλ, Δh географических координат местоположения ИНС и откорректировать их в соответствии с последней тройкой соотношений (1.10).
При необходимости повышения точности определения ошибок счисления координат, после осуществления соответствующих переприсваиваний может быть реализована вторая и последующие итерации.
Представленный выше способ коррекции счисленных ИНС географических координат местоположения объекта по типу коррекции, по используемым при этом информационно-измерительным системам и основным приемам и методам математического преобразования измеренной информации может быть использован в качестве прототипа предлагаемого способа коррекции инерциальной системы по неподвижному ориентиру с известными географическими координатами.
Формализуя приведенное выше описание прототипа, излагая его в терминах, используемых при решении подобных задач математических процедур и с акцентом на физическую суть выполняемых при этом операций, приведем его в следующем виде.
Способ оценивания ошибок Δϕ, Δλ, Δh счисленных инерциальной навигационной системы (ИНС) географических координат ϕ, λ текущего местоположения объекта и комплексной бароинерциальной высоты h его полета и их эпизодической коррекции по результатам кратковременной аппаратной привязки к неподвижному наземному ориентиру коррекции (ОК) с известными географическими координатами ϕ0, λ0, h0 с измерением относительных координат ϕy, ϕz, 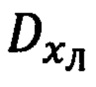 его ориентации, основанный на совместной обработке углов ϕy, ϕz визирования ОК и наклонной дальности
его ориентации, основанный на совместной обработке углов ϕy, ϕz визирования ОК и наклонной дальности 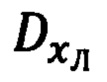 до него, формируемых ИНС текущих углов истинного курса ψи, крена γ и тангажа υ объекта и основной тройки ϕ, λ, h навигационных параметров, в процессе которой по измерениям ϕy, ϕz,
до него, формируемых ИНС текущих углов истинного курса ψи, крена γ и тангажа υ объекта и основной тройки ϕ, λ, h навигационных параметров, в процессе которой по измерениям ϕy, ϕz, 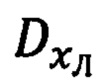 формируют текущие значения компонент Dx, Dy, Dz дальности до ОК в проекциях на оси связанной с объектом системы координат (ССК) Oxyz, которые, используя текущие значения углов ψи, υ, γ ориентации объекта и координат ϕ, λ его местоположения, последовательно приводят к осям географического сопровождающего трехгранника (ГСТ) ONHE и гринвичской системы координат (ГСК) OX'Y'Z', рассчитывая компоненты DN, DH, DE дальности до ОК в проекциях на оси ГСТ ONHE и компоненты
формируют текущие значения компонент Dx, Dy, Dz дальности до ОК в проекциях на оси связанной с объектом системы координат (ССК) Oxyz, которые, используя текущие значения углов ψи, υ, γ ориентации объекта и координат ϕ, λ его местоположения, последовательно приводят к осям географического сопровождающего трехгранника (ГСТ) ONHE и гринвичской системы координат (ГСК) OX'Y'Z', рассчитывая компоненты DN, DH, DE дальности до ОК в проекциях на оси ГСТ ONHE и компоненты 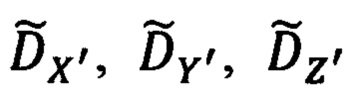 дальности в проекциях на оси ГСК, дополнительно, используя приведенный срез рассчитывают текущие значения гринвичских координат
дальности в проекциях на оси ГСК, дополнительно, используя приведенный срез рассчитывают текущие значения гринвичских координат 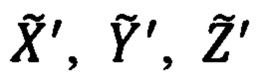 объекта и ОК
объекта и ОК 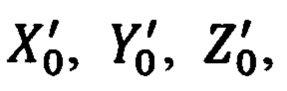 сравнением которых определяют текущие относительные координаты
сравнением которых определяют текущие относительные координаты 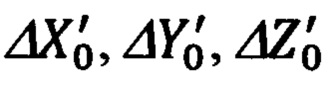 местоположения ОК, а сопоставляя их с соответствующими составляющими DX', DY', DZ' дальности до ОК, формируют систему алгебраических уравнений связи идеальных гринвичских X', Y', Z' и географических ϕ, λ, h координат текущего местоположения объекта, на основе которых, используя прием замены идеальных xj значений координат объекта их адекватным представлением вида
местоположения ОК, а сопоставляя их с соответствующими составляющими DX', DY', DZ' дальности до ОК, формируют систему алгебраических уравнений связи идеальных гринвичских X', Y', Z' и географических ϕ, λ, h координат текущего местоположения объекта, на основе которых, используя прием замены идеальных xj значений координат объекта их адекватным представлением вида 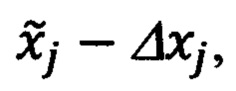 получают уравнения, связывающие ошибки Δϕ, Δλ, Δh счисления географических координат и соответствующие им ошибки ΔХ', ΔY', ΔZ' расчета гринвичских координат, которые известной в теории фигуры Земли подстановкой, связывающей вариации ΔХ', ΔY', ΔZ' гринвичских координат с линейными вариациями
получают уравнения, связывающие ошибки Δϕ, Δλ, Δh счисления географических координат и соответствующие им ошибки ΔХ', ΔY', ΔZ' расчета гринвичских координат, которые известной в теории фигуры Земли подстановкой, связывающей вариации ΔХ', ΔY', ΔZ' гринвичских координат с линейными вариациями 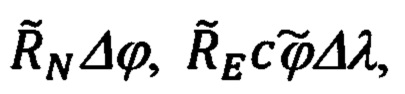 Δh в проекциях на оси ГСТ объекта, приводят к системе алгебраических уравнений относительно Δϕ, Δλ, Δh, решая которую определяют ошибки Δϕ, Δλ, Δh счисления координат и корректируют их счисленные значения
Δh в проекциях на оси ГСТ объекта, приводят к системе алгебраических уравнений относительно Δϕ, Δλ, Δh, решая которую определяют ошибки Δϕ, Δλ, Δh счисления координат и корректируют их счисленные значения 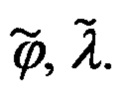
Достоинством указанного способа коррекции является его инвариантность относительно ошибок приведения компонент 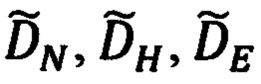 дальности до ОК к осям ГСК OX'Y'Z' и ошибок ΔХ', ΔY', ΔZ' расчета счисленных значений гринвичских координат
дальности до ОК к осям ГСК OX'Y'Z' и ошибок ΔХ', ΔY', ΔZ' расчета счисленных значений гринвичских координат 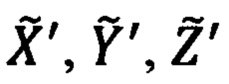 текущего местоположения объекта.
текущего местоположения объекта.
Недостатками указанного способа оптимального оценивания ошибок инерциальной информации и ее коррекции по неподвижному наземному ориентиру с известными географическими координатами являются:
1. Отсутствие математического описания и учета ошибок пересчета компонент Dx, Dy, Dz дальности до ОК в проекциях на оси ССК Oxyz к осям ГСТ ONHE, реализуемого выражениями (1.7) и являющихся следствием ошибочного измерения текущих углов 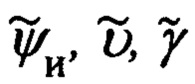 эволюции объекта.
эволюции объекта.
2. Эпизодический, разовый характер коррекции с ограниченным перечнем оцениваемых и корректируемых параметров ИНС, следствием чего является невозможность проведения полноценной коррекции всего перечня пилотажной информации, включая истинный курс объекта, и горизонтальных составляющих его абсолютной линейной скорости.
3. В случае прекращения аппаратного, оптического контакта с используемым для коррекции ориентиром отсутствует возможность реализации не только долгосрочной (до 30÷40-ка минут), но любой процедуры прогноза оцененных ошибок ИНС и проведения по его результатам последующей коррекции.
Техническим результатом изобретения является расширение функциональных возможностей прицельно-навигационного комплекса современного ЛА за счет разработки унифицированной с инерциально-спутниковым режимом коррекции математической процедуры оптимального оценивания ошибок инерциальной информации и ее полноценной коррекции по результатам непрерывного углового сопровождения неподвижного наземного ориентира с известными географическими координатами в обеспечение эффективного решения навигационных, боевых и специальных задач.
Указанный технический результат достигается за счет того, что в способе оптимального оценивания ошибок инерциальной информации и ее коррекции по неподвижному наземному ориентиру с известными географическими координатами, включающем угловое сопровождение неподвижного наземного ориентира коррекции (ОК) и дискретное измерение наклонной дальности до него в щадящем для лазерного дальномера (ЛД) из состава обзорно-прицельной системы (ОПС) режиме его работы с частотой излучающих посылок 0,5-1,0 Гц, основанном на совместной обработке измеряемых при этом текущих углов ϕy, ϕz визирования ОК и наклонной дальности 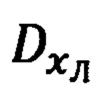 до него, текущих углов истинного
до него, текущих углов истинного 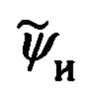 и гироскопического
и гироскопического 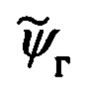 курсов, крена
курсов, крена 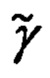 и тангажа
и тангажа 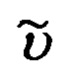 объекта, счисленных ИНС географических координат
объекта, счисленных ИНС географических координат 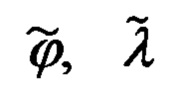 его местоположения и текущей бароинерциальной высоты
его местоположения и текущей бароинерциальной высоты 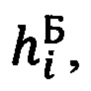 дополнительно, в режиме непрерывного углового сопровождения ОК одно-двух секундные временные интервалы между соседними измерениями дальности до ОК заполняют ее десяти герцовыми расчетными значениями, которые формируют в соответствии с модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедурой определения наклонной дальности, предполагающей использование текущих бароинерциальной высоты объекта, косинуса угла между географической вертикалью и направлением на ОК, и сформированного по измерениям ОПС опорного значения высоты ОК над уровнем моря, при этом оценивание составляющих абсолютной линейной скорости объекта осуществляют в соответствии с кинематической моделью его движения относительно неподвижного наземного ОК в проекциях на оси инерциальной системы координат (ИСК), чем обеспечивают кардинальное упрощение описывающих ее дифференциальных уравнений за счет естественной поканальной декомпозиции модели относительного движения объекта, которую, из соображений повышения точности оценивания, дополнительно, модифицируют, переходя от уравнений для составляющих абсолютной линейной скорости и ускорения объекта в полных сигналах к их вариациям относительно измеренных ИНС текущих значений, при этом компоненты абсолютной линейной скорости движения объекта относительно ОК используют, как известное управление, а полученные в результате процедуры оптимальной фильтрации и идентификации оценки компонент дальности до ОК и составляющих абсолютной линейной скорости объекта используют для формирования позиционных и скоростных сигналов идеального измерителя, путем сравнения которых с соответствующими выходными сигналами ИНС формируют сигналы измерения оптимального фильтра-идентификатора ошибок ИНС и элементы его матрицы наблюдения, через которые осуществляют учет всех ошибок сигналов измерения, при этом процедуру их оптимальной фильтрации и идентификации реализуют в соответствии с традиционной для ИНС моделью ошибок, которую, из соображений корректности ее описания и точности оценивания, расширяют за счет включения в нее трех дифференциальных уравнений, описывающих характер изменения координат местоположения ИНС относительно ОПС в проекциях на оси опорного трехгранника гироплатформы (ОТГП) ИНС, по окончании оптимального оценивания ошибок ИНС, определяемого временем нахождения ОК в зоне оптического контакта с объектом, фильтр-идентификатор ошибок ИНС останавливают, его входные сигналы и коэффициенты усиления обнуляют, а сам фильтр переводят в режим долгосрочного прогноза полученных оценок, который реализуют в соответствии с рекуррентной процедурой формирования априорных ошибок ИНС, а полученные в результате прогноза значения ошибок ИНС используют для коррекции координат текущего местоположения объекта, горизонтальных составляющих его абсолютной линейной скорости, угла азимутальной ориентации ГП ИНС и углов текущей ориентации объекта.
дополнительно, в режиме непрерывного углового сопровождения ОК одно-двух секундные временные интервалы между соседними измерениями дальности до ОК заполняют ее десяти герцовыми расчетными значениями, которые формируют в соответствии с модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедурой определения наклонной дальности, предполагающей использование текущих бароинерциальной высоты объекта, косинуса угла между географической вертикалью и направлением на ОК, и сформированного по измерениям ОПС опорного значения высоты ОК над уровнем моря, при этом оценивание составляющих абсолютной линейной скорости объекта осуществляют в соответствии с кинематической моделью его движения относительно неподвижного наземного ОК в проекциях на оси инерциальной системы координат (ИСК), чем обеспечивают кардинальное упрощение описывающих ее дифференциальных уравнений за счет естественной поканальной декомпозиции модели относительного движения объекта, которую, из соображений повышения точности оценивания, дополнительно, модифицируют, переходя от уравнений для составляющих абсолютной линейной скорости и ускорения объекта в полных сигналах к их вариациям относительно измеренных ИНС текущих значений, при этом компоненты абсолютной линейной скорости движения объекта относительно ОК используют, как известное управление, а полученные в результате процедуры оптимальной фильтрации и идентификации оценки компонент дальности до ОК и составляющих абсолютной линейной скорости объекта используют для формирования позиционных и скоростных сигналов идеального измерителя, путем сравнения которых с соответствующими выходными сигналами ИНС формируют сигналы измерения оптимального фильтра-идентификатора ошибок ИНС и элементы его матрицы наблюдения, через которые осуществляют учет всех ошибок сигналов измерения, при этом процедуру их оптимальной фильтрации и идентификации реализуют в соответствии с традиционной для ИНС моделью ошибок, которую, из соображений корректности ее описания и точности оценивания, расширяют за счет включения в нее трех дифференциальных уравнений, описывающих характер изменения координат местоположения ИНС относительно ОПС в проекциях на оси опорного трехгранника гироплатформы (ОТГП) ИНС, по окончании оптимального оценивания ошибок ИНС, определяемого временем нахождения ОК в зоне оптического контакта с объектом, фильтр-идентификатор ошибок ИНС останавливают, его входные сигналы и коэффициенты усиления обнуляют, а сам фильтр переводят в режим долгосрочного прогноза полученных оценок, который реализуют в соответствии с рекуррентной процедурой формирования априорных ошибок ИНС, а полученные в результате прогноза значения ошибок ИНС используют для коррекции координат текущего местоположения объекта, горизонтальных составляющих его абсолютной линейной скорости, угла азимутальной ориентации ГП ИНС и углов текущей ориентации объекта.
Приведем перечень и описание фигур, которые потребуются при осуществлении предлагаемого изобретения.
Для разработки унифицированной процедуры коррекции ИНС по неподвижному наземному ориентиру с известными географическими координатами целесообразно ввести в рассмотрение следующие системы координат:
- инерциальную систему координат (ИСК) OXYZ;
- гринвическую систему координат (ГСК) OX'Y'Z'.
- географический сопровождающий трехгранник (ГСТ) ONHE;
- опорный трехгранник гироплатформы (ОТГП) ИНС Oξηζ;
- связанную с объектом систему координат (ССК) Oxyz;
- лучевую систему координат (ЛСК) OxЛyЛzЛ.
На фиг. 1 приведена ориентация ИСК OXYZ, ГСК OX'Y'Z' и ГСТ ONHE на земном эллипсоиде вращения. ГСК OX'Y'Z' - это система координат, связанная с Землей, ось ОХ' которой параллельна оси вращения Земли, ось OZ' - лежит в плоскости гринвичского меридиана, а ось OY' дополняет их до правого ортогонального трехгранника и направлена на Запад.
ИСК OXYZ - это абсолютно неподвижная система координат, связанная со звездами. Рассогласование ГСК OX'Y'Z' и ИСК OXYZ определяется углом ut, где u - угловая скорость суточно-годового вращения Земли, t - текущее время (фиг. 1).
На фиг. 2 приведена взаимная ориентация ГСК OX'Y'Z' и ГСТ ONHE.
Их рассогласование определяется углами географической долготы λ и широты ϕ.
Переход от осей ГСК OX'Y'Z' к осям ГСТ ONHE осуществляется посредством двух последовательных поворотов на угол λ и угол ϕ с угловыми скоростями 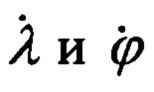 соответственно.
соответственно.
Приведенное на фиг. 2 направление отсчета углов λ и ϕ и угловых скоростей 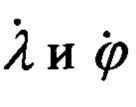 является положительным.
является положительным.
На фиг. 3 приведена взаимная ориентация ГСТ ONHE и ОТГП ИНС Oξηζ. Переход от осей ГСТ ONHE к осям ОТГП ИНС Oξηζ осуществляется посредством поворота на угол χ азимутальной ориентации ОТГП ИНС.
Приведенное на фиг. 3 направление отсчета угла χ и угловой скорости 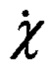 является положительным.
является положительным.
На фиг. 4 приведена взаимная ориентация ОТГП ИНС Oξηζ и ССК Oxyz.
Их рассогласование определяется углами гироскопического курса ψг, тангажа υ и крена γ объекта.
Переход от осей ОТГП Oξηζ к осям ССК Oxyz осуществляется посредством трех последовательных поворотов на углы ψг, υ и γ с угловыми скоростями 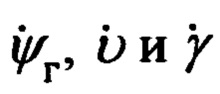 соответственно.
соответственно.
Приведенное на фиг. 4 направление отсчета углов ψг, υ, γ и угловых скоростей 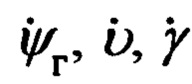 является положительным.
является положительным.
На фиг. 5 приведена взаимная ориентация ССК Oxyz и ЛСК OxЛyЛzЛ.
Их рассогласование определяется углами ϕу, ϕz визирования ОК. Ось ОхЛ ЛСК направлена на ориентир, с указанной осью при угловом сопровождении ОК совпадает вектор  наклонной дальности до него (фиг. 5).
наклонной дальности до него (фиг. 5).
Переход от осей ССК Oxyz к осям ЛСК OxЛyЛzЛ. осуществляется посредством двух последовательных поворотов на углы ϕy и ϕz с угловыми скоростями 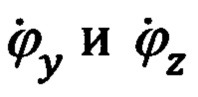 соответственно.
соответственно.
Приведенное на фиг. 5 направление отсчета углов ϕу, ϕz и угловых скоростей 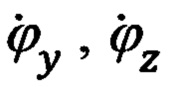 является положительным.
является положительным.
На фиг. 6 приведена взаимная ориентация ГСТ ONHE и ССК Oxyz.
Их рассогласование определяется углами истинного курса ψи, тангажа υ и крена γ объекта.
Переход от осей ГСТ ONHE к осям ССК Oxyz осуществляется посредством трех последовательных поворотов на углы ψи, υ и γ с угловыми скоростями 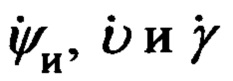 соответственно.
соответственно.
Приведенное на фиг. 6 направление отсчета углов ψи, υ и γ и угловых скоростей 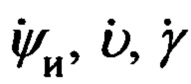 является положительным.
является положительным.
На фиг. 7 представлен примерный план полета объекта относительно наземного ориентира коррекции ОК при его угловом сопровождении в обеспечение коррекции ИНС.
Оптический контакт с ОК и его угловое сопровождение начинается с дальности DK до точки К касания с окружностью радиуса rц, по которой осуществляется циркуляция объекта.
Для вертолета представленные на фиг. 7 параметры при скорости его полета V=144 км/ч могут быть приняты равными DK=3-4 км, rц=1,2-1,5 км. При указанных значениях параметров время оптического контакта с ОК и его углового сопровождения составит порядка 337-360 секунд, что позволит реализовать полноценную процедуру оценивания и коррекции ИНС.
Для боевого самолета указанные параметры могут быть определены и уточнены по результатам натурных работ.
С целью раскрытия физической и математической сути предлагаемого способа коррекции приведем подробное описание используемых при этом векторно-матричных и скалярных преобразований, дифференциальных уравнений относительного движения объекта и входящих в них параметров, а также оптимальных математических процедур линейной дискретной фильтрации и идентификации Калмана.
Но прежде, несколько уточняющих и предваряющих дальнейшее исследование моментов, имеющих принципиальное значение.
В дальнейшем будем полагать, что географические координаты ориентира коррекции являются абсолютно точными и равны ϕ0, λ0, h0, где под h0 следует понимать высоту ОК над уровнем моря.
Под используемым понятием «унифицированный способ оптимального оценивания…» следует понимать его алгоритмическую и программную унификацию с той процедурой оптимальной фильтрации и идентификации, которая используется при оптимальном оценивании ошибок ИНС в режиме инерциально-спутниковой коррекции. При этом допускается некоторые различия рассматриваемых процедур, определяемые вариациями их матриц наблюдения. Матрицы сообщения, определяемые моделью ошибок ИНС, в рассматриваемых случаях должны быть адекватны.
Учитывая, что процедура оптимального оценивания в режиме инерциально-спутниковой коррекции ИНС является достаточно отработанной, цель настоящего исследования будет заключаться в рассмотрении только тех специфических вопросов оценивания и коррекции по сопровождаемому теле- или тепловизионным каналом обзорно-прицельной системы (ОПС) ориентиру коррекции, которые позволяли бы максимально эффективно адаптировать их к инженерно-отработанному алгоритму инерциально-спутниковой коррекции.
Представляется, что для этого необходимо и достаточно в процессе углового сопровождения ОК по производимым ОПС измерениям и подлежащей коррекции навигационной и пилотажной информации ИНС (с учетом ошибок ее измерения и счисления) сформировать необходимые для реализации рассматриваемого режима коррекции значения географических координат текущего местоположения объекта и горизонтальных составляющих его абсолютной линейной скорости, которые в штатной процедуре инерциально-спутниковой коррекции используются в качестве сигналов измерителя.
Условимся, что обзорно-прицельная система является идеальным датчиком первичной информации, поэтому производимые ей измерения углов ϕy, ϕz визирования ОК и опорных значений наклонной дальности 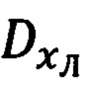 до него будем считать абсолютно точными.
до него будем считать абсолютно точными.
Учитывая, что длительность процедуры оптимального оценивания ошибок инерциальной информации должна составлять 5-6 минут, а на работу лазерного дальномера (ЛД) в режиме 10-ти герцового измерения дальности есть временные ограничения, предлагается использовать ЛД в режиме низкочастотного измерения дальности (f=0,5-1 Гц) с заполнением интервалов между опорными измерениями дальностей их расчетными значениями, полученными на основе модифицированного угломестного способа их определения.
С целью раскрытия физической сути и математического содержания предлагаемых алгоритмических решений приведем все необходимые векторно-матричные соотношения, в соответствии с которыми могут быть реализованы взаимные преобразования компонент произвольного вектора для введенных в рассмотрение систем координат.
Векторно-матричные выражения для преобразования компонент произвольного вектора, заданных проекциями на оси ГСК OX'Y'Z', к осям ГСТ ONHE и обратно будут иметь следующий вид:

Входящие в выражения (3), (4) матрица G и транспонированная матрица GT, имеют вид:


Векторно-матричное выражение для расчета компонент произвольного вектора в проекциях на оси ОТГП ИНС Oξηζ по известным его составляющим в проекциях на оси ГСТ ONHE и обратное ему выражение будут иметь вид:

где матрица Г и транспонированная матрица ГТ, в соответствии с фиг. 3, равны:

Векторно-матричное выражение для расчета компонент произвольного вектора в проекциях на оси ССК Oxyz по известным его составляющим в осях ОТГП ИНС Oξηζ и обратное ему выражение имеют вид:

где матрица S0 и транспонированная матрица 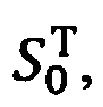 в соответствии с фиг. 4, имеют вид:
в соответствии с фиг. 4, имеют вид:
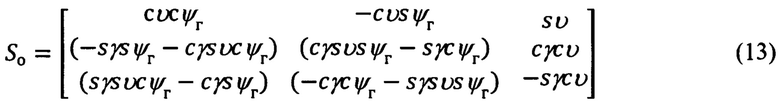
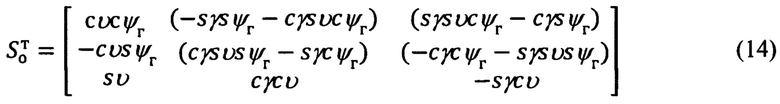
Векторно-матричное выражение для расчета компонент произвольного вектора в проекциях на оси ЛСК OxЛyЛzЛ по известным его составляющим в проекциях на оси ССК Oxyz и обратное ему выражение имеют вид:

Входящие в (15) матрицы L и LT, в соответствии с фиг. 5, равны:

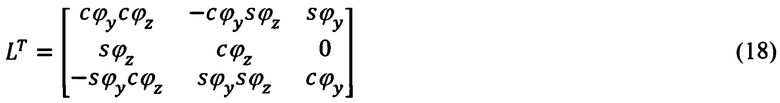
Для расчета компонент произвольного вектора в проекциях на оси ИСК OXYZ по известным его компонентам в проекциях на оси ЛСК OxЛyЛzЛ необходимо знать соответствующую этому преобразованию матрицу.
Для определения вида указанной матрицы найдем предварительно матрицу для расчета компонент произвольного вектора в проекциях на оси ГСК OX'Y'Z' по известным его составляющим в осях ЛСК OxЛyЛzЛ.
Согласно (4), (8), (12) и (16), преобразование произвольного вектора, заданного в осях ЛСК, к осям гринвичской системы координат ГСК OX'Y'Z' может быть осуществлено в соответствии со следующим матричным выражением:

В соответствии с приведенным выражением матрица рассматриваемого преобразования равна 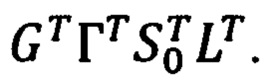
Для преобразования произвольного вектора, заданного проекциями на оси лучевой системы координат, под которым следует понимать измеренный лазерным дальномером массив наклонной дальности, к осям инерциальной системы отсчета воспользуемся полученным выше матричным соотношением (19), в котором под матрицей GT (6) будем понимать аналогичную по структуре матрицу с той лишь разницей, что в ней вместо географической долготы λ, отсчитываемой от плоскости гринвического меридиана, будем использовать абсолютную долготу λа, равную:

где u - угловая скорость суточно-годового вращения Земли 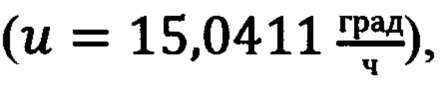 a tk - текущее время, которое рассчитывается в соответствии со следующим рекуррентным выражением:
a tk - текущее время, которое рассчитывается в соответствии со следующим рекуррентным выражением:

где τ - дискрет счета, который для рассматриваемой задачи равен 0,1 сек, t0=0.
Отсчет абсолютной долготы λа осуществляется относительно оси OZ (фиг. 1), при этом угол между указанной осью и осью OZ', равен разнице абсолютной λа и географической λ долготы.
При расчете текущего времени tk (21) его отсчет необходимо вести относительно начала конкретного режима, в котором используется рассматриваемое векторно-матричное преобразование:

где GT (ϕ, λа) - матрица, структурно аналогичная матрице GT (6), но в функции ϕ и λа (20).
Векторно-матричное выражение, обратное приведенному (22), будет иметь вид:

где G (ϕ, λа) - матрица, структурно аналогичная матрице G (5), но в функции абсолютной долготы λа (20).
В соответствии с векторно-матричными выражениями (3) и (7), а также принимая во внимание (23), выражение для расчета составляющих произвольного вектора в проекциях на оси ОТГП Oξηζ по известным его компонентам, представленных в осях ИСК OXYZ, и обратное ему выражение имеют следующий вид:
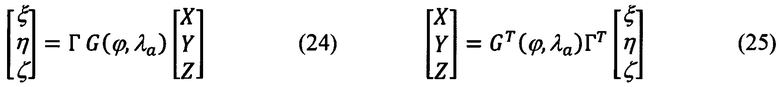
Векторно-матричное выражение для расчета компонент произвольного вектора в проекциях на оси ССК Oxyz по известным его составляющим в проекциях на оси ГСТ ONHE и обратное ему выражение имеют вид:

где матрица Sг и транспонированная (обратная) матрица 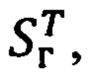 в соответствии с фиг. 6, равны:
в соответствии с фиг. 6, равны:
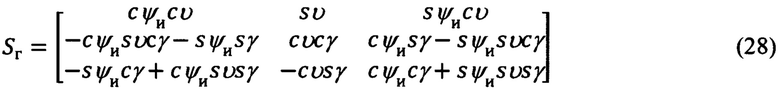
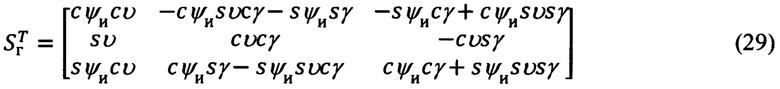
В соответствии с (3), (26) и (4), (27), используя в выражениях (3) и (4) вместо матриц G и GT их абсолютные аналоги G (ϕ, λа) и GT (ϕ, λа), получают векторно-матричное выражение для расчета компонент произвольного вектора в проекциях на оси ССК Oxyz по известным его составляющим в осях ИСК OXYZ, а также обратное ему выражение. Приведем их:
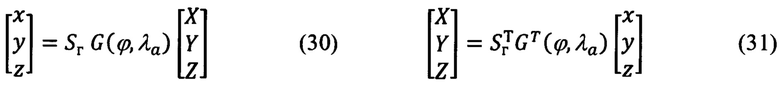
Приведенные выше векторно-матричные преобразования и входящие в них матрицы позволяют реализовать дискретную математическую процедуру оптимального оценивания составляющих абсолютной линейной скорости объекта на основе рекуррентной процедуры линейной фильтрации и идентификации составляющих дальности до ОК в проекциях на оси ИСК OXYZ, наблюдаемых на фоне случайных некоррелированных шумов измерения.
В частности, векторно-матричное выражение (31) будет использовано для расчета составляющих 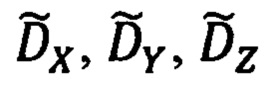 дальности до ОК по рассчитанным, в соответствии с (16), составляющим Dx, Dy, Dz дальности в проекциях на оси ССК Oxyz.
дальности до ОК по рассчитанным, в соответствии с (16), составляющим Dx, Dy, Dz дальности в проекциях на оси ССК Oxyz.
Как следует из выражения (16), при расчете составляющих Dx, Dy, Dz используют измеренные ОПС значения углов ϕy, ϕz визирования ОК (18) и текущее значение наклонной дальности до него.
Полученные по результатам оптимальной фильтрации оценки 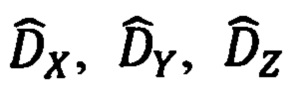 компонент дальности до ОК в проекциях на оси ИСК, в соответствии с векторно-матричным выражением вида:
компонент дальности до ОК в проекциях на оси ИСК, в соответствии с векторно-матричным выражением вида:

приводят к осям ГСТ ONHE и используют для формирования географических координат текущего местоположения объекта, которые используют в качестве позиционных сигналов идеального измерителя.
Дополнительно, в соответствии с векторно-матричным выражением (24) осуществляют приведение оцениваемых составляющих 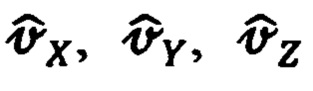 абсолютной линейной скорости объекта к осям ОТГП Oξηζ и последующее их использование в качестве скоростных сигналов идеального измерителя.
абсолютной линейной скорости объекта к осям ОТГП Oξηζ и последующее их использование в качестве скоростных сигналов идеального измерителя.
При этом, по сформированным ниже позиционным и скоростным сигналам идеального измерителя и текущим значениям счисленных инерциальной системой географических координат местоположения и горизонтальных составляющих абсолютной линейной скорости объекта, формируют входные сигналы оптимального фильтра-идентификатора, реализующего оптимальное оценивание ошибок ИНС.
В дальнейшем, все относящееся к оптимальному оцениванию ошибок ИНС будем трактовать, как основную процедуру оптимальной фильтрации и идентификации.
При этом под вспомогательной процедурой оптимального оценивания будем понимать процедуру, осуществляемую в соответствии с дифференциальными уравнениями движения объекта относительно неподвижного наземного ориентира коррекции в проекциях на оси ИСК OXYZ.
Ее основное назначение - оптимальная фильтрация измеренных/рассчитанных компонент 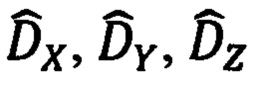 дальности и оценивание составляющих
дальности и оценивание составляющих 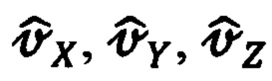 абсолютной линейной скорости объекта с их последующим использованием для формирования позиционных и скоростных сигналов измерителя в обеспечение реализации основной процедуры оценивания.
абсолютной линейной скорости объекта с их последующим использованием для формирования позиционных и скоростных сигналов измерителя в обеспечение реализации основной процедуры оценивания.
И в этом смысле указанная процедура, действительно, является вспомогательной, выполняющей функции информационного обеспечения оптимального оценивания текущих ошибок инерциальной системы.
То обстоятельство, что вспомогательная процедура оптимального оценивания осуществляется в соответствии с моделью относительного движения объекта в проекциях на оси ИСК OXYZ является неслучайным, поскольку только в этом случае дифференциальные уравнения движения объекта относительно ОК упрощаются настолько, что принимают вид трех поканально независимых систем дифференциальных уравнений первого порядка. Получим их.
В соответствии с известной леммой о нахождении абсолютной производной некоторого вектора, приведенной в «Курсе теоретической механики» Л.Г. Лойцянского, А.И. Лурье, Том 1, Москва, «Наука», 1982 г [2] (стр. 301-302) можно показать, что векторное дифференциальное уравнение относительного движения цели имеет вид:

где 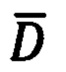 - вектор дальности между объектом и целью;
- вектор дальности между объектом и целью; 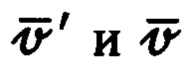 - векторы абсолютной линейной скорости цели и объекта соответственно;
- векторы абсолютной линейной скорости цели и объекта соответственно; 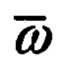 - вектор абсолютной угловой скорости вращения подвижной системы координат Oxyz;
- вектор абсолютной угловой скорости вращения подвижной системы координат Oxyz; 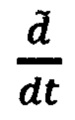 - символ локальной производной.
- символ локальной производной.
При скалярном представлении векторного уравнения (33) необходимо помнить, что оно должно быть записано в проекциях на оси подвижной системы координат Oxyz. Если в качестве подвижной выбрана ССК Oxyz, составляющие 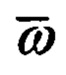 абсолютной угловой скорости которой равны ωx, ωу, ωz, то в этом случае система скалярных уравнений относительного движения цели будет иметь следующий вид:
абсолютной угловой скорости которой равны ωx, ωу, ωz, то в этом случае система скалярных уравнений относительного движения цели будет иметь следующий вид:

Приведенной системой дифференциальных уравнений описывается относительное движение объекта и цели в самом общем случае. Указанную структуру будут иметь дифференциальные уравнения в проекциях на оси ГСТ ONHE, ОТГП Oξηζ.
Из этого ряда выпадают дифференциальные уравнения в проекциях на оси ЛСК OxЛyЛzЛ и ГСК OX'Y'Z'. Особое место в этом ряду занимает случай, когда в качестве подвижной принимается абсолютно неподвижная система координат, а именно, ИСК OXYZ.
Принципиальное отличие этого варианта от представленных выше является то, что абсолютная угловая скорость подвижной (инерциальной) системы координат относительно неподвижной (инерциальной) системы координат будет равна нулю, т.е. ωХ=ωY=ωZ=0, что приводит к закономерному упрощению представленной выше системы дифференциальных уравнений (34), которая в этом случае принимает вид:

Впервые на указанное свойство ИСК OXYZ применительно к модели относительного движения цели обратили внимание в учебнике Р.В. Мубаракшина, В.М. Балуева, Б.В. Воронова «Прицельные системы стрельбы», часть 1, ВВИА им. Н.Е. Жуковского, 1973 г, [3] (стр. 49, с 5-ой по 9-ую строки сверху).
Для формирования полной модели относительного движения цели необходимо дифференциальные уравнения (35) дополнить уравнениями, описывающими характер изменения скорости цели для случая ее движения с постоянным ускорением. В соответствии с упомянутой выше леммой [2], устанавливающей порядок определения абсолютной производной в подвижной системе координат, указанные уравнения будут иметь следующий вид:



Полагая в приведенных уравнениях составляющие 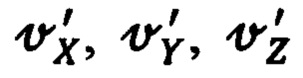 абсолютной линейной скорости движения цели - в рассматриваемом случае, ориентира коррекции, известными, поскольку известны его географические координаты, и ускорения - равными нулю, а составляющие
абсолютной линейной скорости движения цели - в рассматриваемом случае, ориентира коррекции, известными, поскольку известны его географические координаты, и ускорения - равными нулю, а составляющие 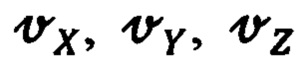 абсолютной скорости и ускорения аХ, aY, aZ движения объекта подлежащими оптимальному оцениванию, запишем их в следующем измененном виде:
абсолютной скорости и ускорения аХ, aY, aZ движения объекта подлежащими оптимальному оцениванию, запишем их в следующем измененном виде:



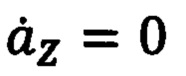
Таким образом, система из трех поканально независимых дифференциальных уравнений (36), (37), (38), которая в режиме привязки к подвижной цели используется для оптимального оценивания параметров ее движения, в ее измененном представлении (39), (40), (41) предназначена для оптимальной фильтрации и идентификации параметров движения объекта относительно неподвижного наземного ориентира, осуществляемой, как и в режиме привязки к цели, по измерениям дальности до ориентира коррекции, наблюдаемых на фоне случайных некоррелированных шумов измерения VX, VY, VZ:

Входящие в (39), (40), (41) составляющие абсолютной линейной скорости ОК в проекциях на оси ГСТ ONHE обусловлены угловой скоростью суточно-годового вращения Земли и равны:

Расчет составляющих  в проекциях на оси ИСК, может быть осуществлен в соответствии с векторно-матричным выражением, обратным (32):
в проекциях на оси ИСК, может быть осуществлен в соответствии с векторно-матричным выражением, обратным (32):

В выражениях (43), (44) ϕ0, λ0, h0 - это географические координаты ОК, при этом его абсолютная долгота λа равна:

Учитывая, что в рассматриваемом режиме коррекции в процессе оптимального оценивания ошибок ИНС объект после подлета к ориентиру коррекции переходит в режим циркуляции с последующим выходом на предписанный заданием курс (фиг. 7), для гарантированно точного оценивания составляющих абсолютной линейной скорости и ускорения объекта представляется целесообразным от варианта оценивания в полных сигналах (39), (40), (41) перейти к варианту оценивания ошибок 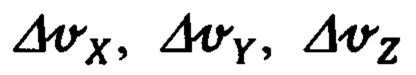 измеренных инерциальной системой составляющих
измеренных инерциальной системой составляющих 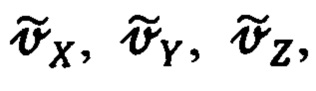 подчиняющимся соотношениям вида:
подчиняющимся соотношениям вида:

где 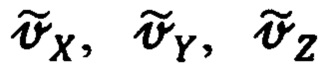 - измеренные/рассчитанные ИНС составляющие абсолютной линейной скорости объекта, приведенные к осям ИСК (25).
- измеренные/рассчитанные ИНС составляющие абсолютной линейной скорости объекта, приведенные к осям ИСК (25).
Подставляя (46) в дифференциальные уравнения (39), (40), (41) и переходя в уравнениях для составляющих скорости и ускорения к их вариациям, получим следующую модифицированную систему уравнений:



Приведенный прием модификации дифференциальных уравнений относительного движения объекта позволит практически устранить возможные динамические ошибки оценивания абсолютной линейной скорости объекта на циркуляции.
Входящие в уравнения (47), (48), (49) составляющие 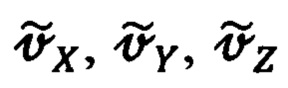 абсолютной линейной скорости объекта формируются посредством применения к измеренным инерциальной системой горизонтальным составляющим
абсолютной линейной скорости объекта формируются посредством применения к измеренным инерциальной системой горизонтальным составляющим 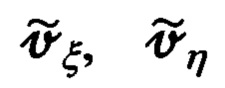 абсолютной линейной скорости объекта матричного преобразования вида (25):
абсолютной линейной скорости объекта матричного преобразования вида (25):

Составляющие скорости 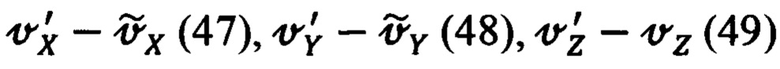 в процедуре оптимального оценивания используются, как известные управления.
в процедуре оптимального оценивания используются, как известные управления.
При этом текущие оценки составляющих 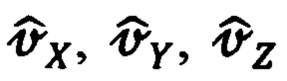 абсолютной линейной скорости объекта рассчитываются в соответствии с выражениями вида (46):
абсолютной линейной скорости объекта рассчитываются в соответствии с выражениями вида (46):

где  оценки ошибок измеряемых ИНС составляющих абсолютной линейной скорости (46).
оценки ошибок измеряемых ИНС составляющих абсолютной линейной скорости (46).
Приведенные выше уравнения (47), (48), (49) предназначены для синтеза вспомогательной процедуры оптимальной фильтрации и идентификации сигналов измерения (42) и оценивания ошибок 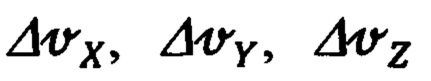 измерения счисленных инерциальной системой составляющих
измерения счисленных инерциальной системой составляющих 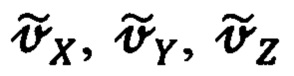 абсолютной линейной скорости, поскольку разработанную на их основе математическую процедуру оптимального оценивания будет отличать высокая степень их поканальной унификации, простота алгоритмической и программной реализации, высокое быстродействие и точность.
абсолютной линейной скорости, поскольку разработанную на их основе математическую процедуру оптимального оценивания будет отличать высокая степень их поканальной унификации, простота алгоритмической и программной реализации, высокое быстродействие и точность.
Приведем сводку используемых при оптимальном оценивании соотношений, представленную в Э. Сейдж, Дж. Мелс «Теория оценивания и ее применение в связи и управлении», «Связь», Москва, 1976, [4] (стр. 269).
Приведенная ниже процедура оптимального оценивания будет использована и при синтезе фильтра-идентификатора в обеспечение оценивания ошибок ИНС.
1. Исходная модель сообщения:

2. Модель наблюдения:

3. Априорные данные, используемые при синтезе:
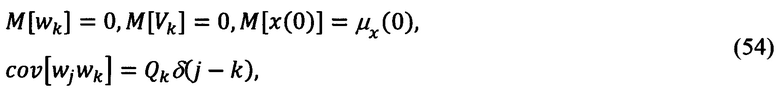
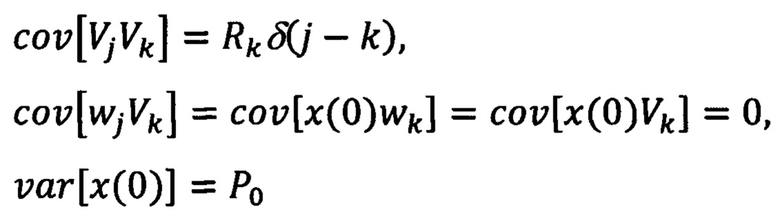
4. Структура оптимального фильтра:
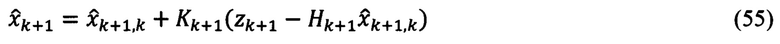
где 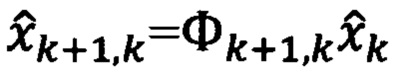
5. Вычисление оптимальных коэффициентов усиления:
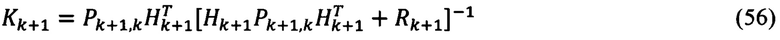
6. Вычисление матрицы априорных ошибок оценивания:
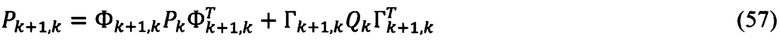
7. Вычисление матрицы апостериорных ошибок оценивания:

В приведенных выше соотношениях приняты следующие условные обозначения:
xk - вектор параметров состояния системы;
 - вектор оптимальных апостериорных оценок параметров состояния;
- вектор оптимальных апостериорных оценок параметров состояния;
wk - вектор случайных возмущений системы (модели сообщения);
Vk - вектор случайных шумов измерения;
Фk+1,k - фундаментальная матрица системы (модели сообщения);
Гk+1,k - матрица передачи случайных возмущений системы;
Hk - матрица измерения;
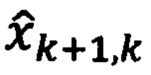 - вектор априорных оценок параметров состояния системы;
- вектор априорных оценок параметров состояния системы;
Pk+1,k - априорная корреляционная матрица ошибок оценивания;
Pk+1 - апостериорная корреляционная матрица ошибок оценивания;
Qk - корреляционная матрица случайных шумов системы;
Rk - корреляционная матрица случайных шумов измерения;
zk - вектор сигналов измерения;
Kk+1 - матрица оптимальных коэффициентов усиления.
Приведем некоторые соображения, касающиеся точности оценивания составляющих абсолютной линейной скорости объекта.
Предположение, что все измерения, производимые обзорно-прицельной системой, являются абсолютно точными, означает безошибочность расчета компонент Dx, Dy, Dz дальности до ОК в проекциях на оси ССК Oxyz.
При ошибочно измеренных углах ψи, υ, γ эволюции объекта и счисленных географических координатах ϕ, λ его текущего местоположения, составляющие DX, DY, DZ дальности до ОК в проекциях на оси ИСК OXYZ, будут рассчитаны с ошибками, обусловленными, исключительно, пересчетами компонент дальности от осей ССК Oxyz к осям ГСТ ONHE и далее - к осям ИСК OXYZ.
Ошибки расчета компонент DX, DY, DZ дальности приведут к соответствующим и согласованным с ними ошибкам определения составляющих 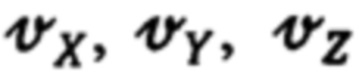 абсолютной линейной скорости объекта. Для корректно организованной линейной процедуры оптимальной фильтрации и идентификации согласованность ошибок рассматриваемых параметров в проекциях на оси ИСК является следствием асимптотической сходимости их оптимальных оценок.
абсолютной линейной скорости объекта. Для корректно организованной линейной процедуры оптимальной фильтрации и идентификации согласованность ошибок рассматриваемых параметров в проекциях на оси ИСК является следствием асимптотической сходимости их оптимальных оценок.
Обратный пересчет, но уже оценок компонент 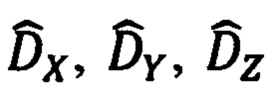 дальности к осям ССК Oxyz приведет к ожидаемому устранению ошибок прямого преобразования.
дальности к осям ССК Oxyz приведет к ожидаемому устранению ошибок прямого преобразования.
Таким образом, как ошибочность дискретного массива компонент дальности до ОК в проекциях на оси ИСК являлась причиной ошибочного оценивания составляющих 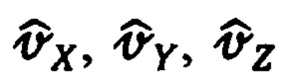 абсолютной линейной скорости объекта в инерциальных осях, так и безошибочность оценок компонент
абсолютной линейной скорости объекта в инерциальных осях, так и безошибочность оценок компонент 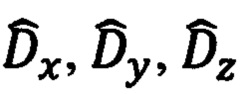 дальности в связанных осях, учитывая их согласованность с соответствующими оценками составляющих
дальности в связанных осях, учитывая их согласованность с соответствующими оценками составляющих 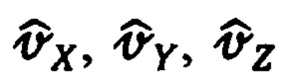 абсолютной линейной скорости, следует рассматривать как необходимое и достаточное условие безошибочного определения последних в осях ССК Oxyz.
абсолютной линейной скорости, следует рассматривать как необходимое и достаточное условие безошибочного определения последних в осях ССК Oxyz.
На основании вышеизложенного, далее, при формировании позиционных и скоростных сигналов измерения и определении соответствующих им элементов матрицы наблюдения будем считать, что оценки компонент 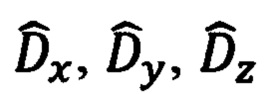 дальности до ориентира коррекции и составляющих
дальности до ориентира коррекции и составляющих 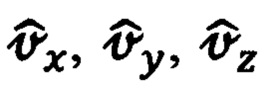 абсолютной линейной скорости в проекциях на оси ССК Oxyz являются абсолютно точными.
абсолютной линейной скорости в проекциях на оси ССК Oxyz являются абсолютно точными.
Дальнейшее использование рассматриваемых оценок 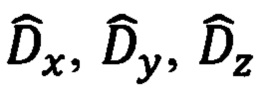 дальности и составляющих
дальности и составляющих 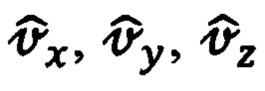 абсолютной линейной скорости предполагает приведение первых к осям ГСТ ONHE, а вторых -
абсолютной линейной скорости предполагает приведение первых к осям ГСТ ONHE, а вторых - 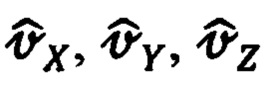 - к осям ОТГП ИНС Oξηζ.
- к осям ОТГП ИНС Oξηζ.
Учитывая характер указанных преобразований, следует ожидать, что ошибки координат текущего местоположения объекта будут определяться ошибками измерения углов 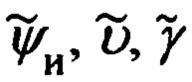 эволюции объекта и счисления географической широты
эволюции объекта и счисления географической широты 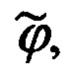 а составляющих его абсолютной линейной скорости
а составляющих его абсолютной линейной скорости 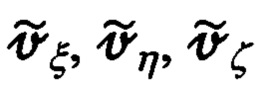 - ошибками измерения углов
- ошибками измерения углов 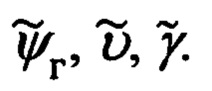
Приведем все необходимые вспомогательные операции для получения скоростных и позиционных уравнений связи и формирования на их основе сигналов измерения по скорости и координатам, а также соответствующих им элементов матрицы наблюдения основной процедуры оптимального оценивания.
Математический прием, который будет использован при этом, эффективно себя зарекомендовал при разработке алгоритмов оптимального оценивания и коррекции ИНС по измерениям спутниковой навигационной системы (СНС) и доплеровского измерителя составляющих скорости (ДИСС).
С такой же эффективностью он может быть использован и в рассматриваемой процедуре оптимального оценивания и коррекции.
При этом, для идеальных навигационных сигналов используют выражения (1.10), а для пилотажных - соотношения вида:

где 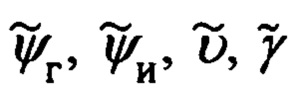 - измеренные значения соответствующих углов; Δψг, Δψи, Δυ, Δγ - ошибки их измерения.
- измеренные значения соответствующих углов; Δψг, Δψи, Δυ, Δγ - ошибки их измерения.
Эффективность использования указанного приема обусловлена тем, что введенные в рассмотрение ошибки навигационных Δϕ, Δλ, Δχ и пилотажных Δψг, Δψи, Δυ, Δγ параметров могут быть представлены в функции малых углов αx, αy, αz рассогласования реального и опорного трехгранников ГП ИНС, а именно:


А то обстоятельство, что углы αx, αу, αz входят в перечень оцениваемых параметров состояния ИНС, позволяет автоматизировать учет представленных выше ошибок (60), (61) счисления навигационных и измерения пилотажных параметров в рамках штатной процедуры оптимального оценивания путем корректного формирования позиционных и скоростных элементов матрицы наблюдения.
Приведем подробное описание процедуры формирования скоростных сигналов измерения и соответствующих элементов матрицы наблюдения.
Учитывая, что оценивание ошибок ИНС осуществляется в соответствии с системой дифференциальных уравнений ошибок ИНС, представленной в проекциях на оси ОТГП Oξηζ, необходимо полученные, в соответствии с векторно-матричным выражением вида (30), составляющие оценок 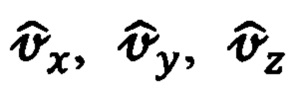 абсолютной линейной скорости объекта привести к осям ОТГП Oξηζ.
абсолютной линейной скорости объекта привести к осям ОТГП Oξηζ.
Для этого воспользуемся векторно-матричным преобразованием (12), в котором используемая при его реализации матрица 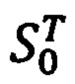 имеет вид (14).
имеет вид (14).
Представляя выражение (12) в скалярном виде, в соответствии с (14), получим:
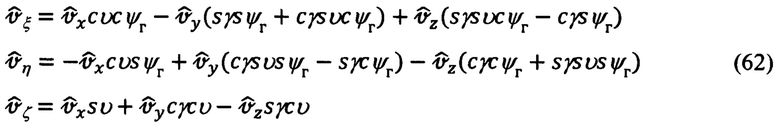
Подставляя в (62) идеальные значения углов ψг, υ, γ (59), получим следующее промежуточное представление выражений для 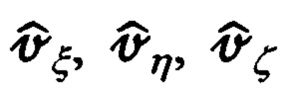 в функции измеренных углов
в функции измеренных углов 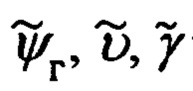 эволюции объекта и ошибок Δψг, Δυ, Δγ их измерения:
эволюции объекта и ошибок Δψг, Δυ, Δγ их измерения:
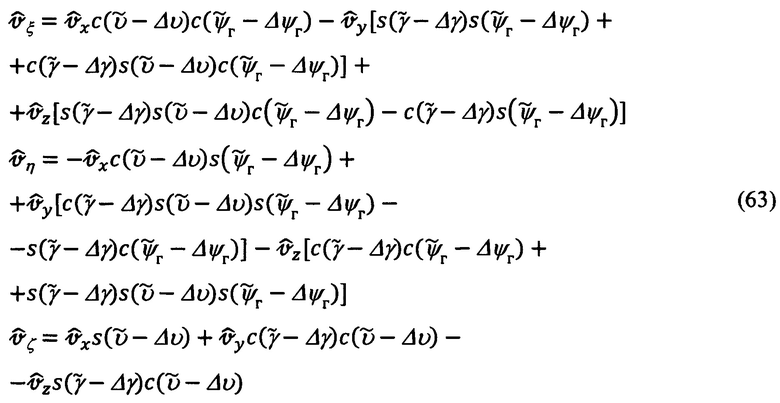
Перепишем приведенные выражения, раскрывая в них синусы и косинусы двух углов, полагая углы Δψг, Δυ, Δγ малыми:
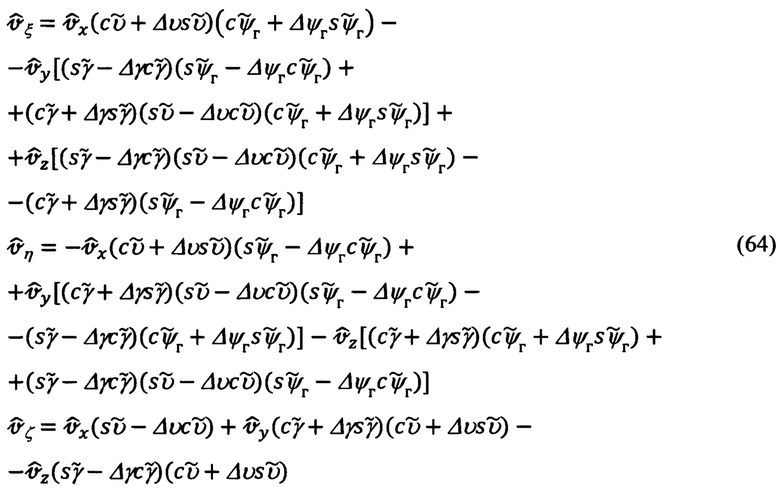
Раскрывая приведенные выражения, пренебрегая при этом величинами 2-го и более порядка малости относительно Δψг, Δυ, Δγ, получим следующее представление для рассматриваемых составляющих абсолютной линейной скорости:
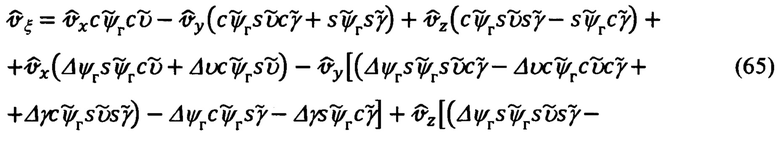
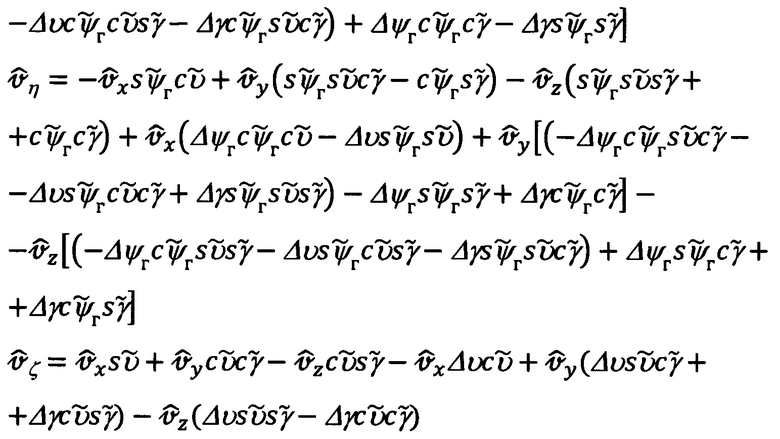
Полученные выше выражения (65) для горизонтальных составляющих 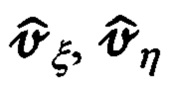 абсолютной линейной скорости объекта целесообразно представить в следующем виде:
абсолютной линейной скорости объекта целесообразно представить в следующем виде:

где расчетные составляющие 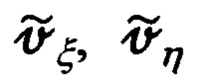 абсолютной линейной скорости объекта и ошибки
абсолютной линейной скорости объекта и ошибки 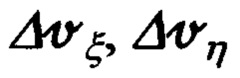 их расчета, в соответствии с выражениями (65), будут равны:
их расчета, в соответствии с выражениями (65), будут равны:
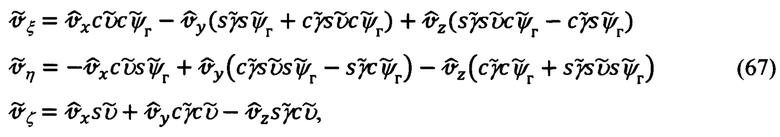
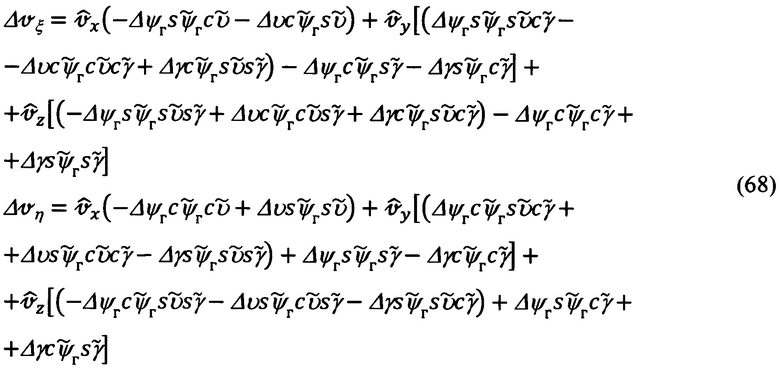
Для формирования сигналов измерения по скорости запишем выражения для горизонтальных составляющих Vx, Vy абсолютной линейной скорости, измеряемых ИНС.
Как показывает опыт вывода дифференциальных уравнений, описывающих характер изменения ошибок ИНС, традиционной и самой распространенной формой представления ее выходных сигналов по скорости является представление вида:

где: Vξ, Vη, Vζ - составляющие абсолютной линейной скорости в проекциях на оси ОТГП ИНС Oξηζ; ΔVx, ΔVy - ошибки их измерения/вычисления; αx, αу, αz - введенные выше в рассмотрение малые углы рассогласования реального и опорного трехгранников ГП ИНС.
Составляющие Vξ, Vη, Vζ - это компоненты абсолютной линейной скорости объекта, измеряемые ИНС в случае ее идеального функционирования.
С учетом кинематических составляющих ΔVξ, ΔVη, ΔVζ скорости, имеющих место при различном конструктивном размещении на объекте обзорно-прицельной и инерциальной систем и выполнении им маневра, типа «циркуляции» (фиг. 7), приведенные выше выражения (69) должны быть уточнены и представлены в следующем виде:
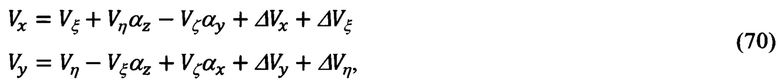
Записывая полученные выше выражения (66) в несколько измененном виде:

и сравнивая их с соответствующими выражениями, описывающими выходные сигналы ИНС (70), получим следующие уравнения связи:
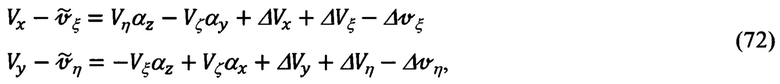
Левые части приведенных уравнений связи (72) - это результат сравнения соответствующих составляющих абсолютной линейной скорости, измеренных ИНС (70) и сформированных по измерениям ОПС (71).
Обозначим их через z3 и z4 и в дальнейшем будем трактовать их, как сигналы измерения оптимального фильтра-идентификатора ошибок ИНС:

Выражения (73) являются легко реализуемыми, поскольку используемые при их формировании сигналы либо измеряются (Vx, Vy), либо вычисляются 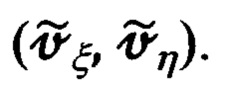
По виду правой части уравнений (72) определяют скоростные элементы матрицы наблюдения, используемой в основной процедуре оценивания при расчете оптимальных коэффициентов усиления (56), апостериорной матрицы ошибок оценивания (58), а также при расчете оптимальных оценок параметров состояния ИНС (55).
Но для этого необходимо знать состав вектора параметров состояния ИНС и математическое описание кинематических составляющих ΔVξ, ΔVη, ΔVζ скорости (70) и компонент 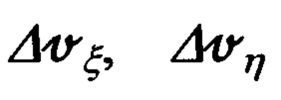 (68) скорости, характеризующих ошибки расчета составляющих (67), (71).
(68) скорости, характеризующих ошибки расчета составляющих (67), (71).
Для описания последних 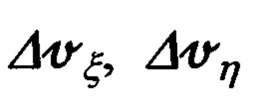 (68) в функции входящих в перечень параметров состояния ИНС малых углов, характеризующих погрешности αx, αу выдерживания вертикали и азимутального ухода αz гироплатформы ИНС, воспользуемся кинематическими соотношениями связи (61).
(68) в функции входящих в перечень параметров состояния ИНС малых углов, характеризующих погрешности αx, αу выдерживания вертикали и азимутального ухода αz гироплатформы ИНС, воспользуемся кинематическими соотношениями связи (61).
Но прежде, преобразуем полученные выше выражения (68) для 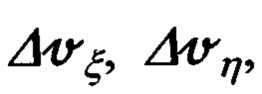 группируя их по ошибкам Δψг, Δυ, Δγ измерения углов эволюции объекта:
группируя их по ошибкам Δψг, Δυ, Δγ измерения углов эволюции объекта:
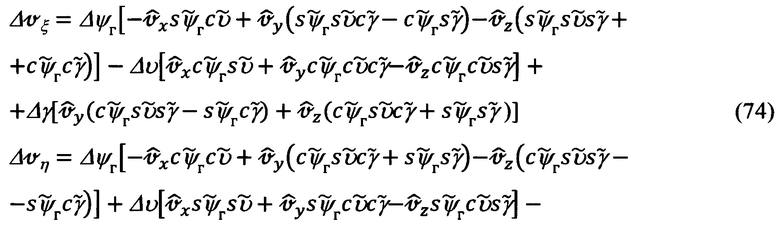
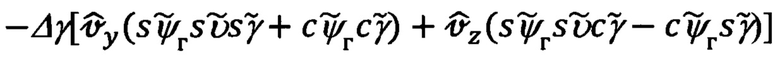
Выражения (74), в соответствии с выражениями для 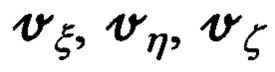 (67) и видом матрицы
(67) и видом матрицы 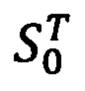 (14), запишем в более компактном виде:
(14), запишем в более компактном виде:
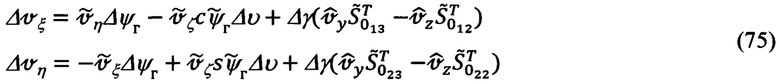
Подстановка в выражения (75) вместо малых углов Δψг, Δυ, Δγ ошибок измерения текущих углов ориентации объекта их значений, определяемых соотношениями (61), приводит к выражениям вида:
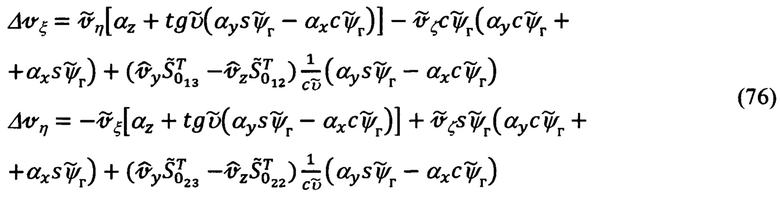
После приведения подобных членов полученные выражения примут вид:
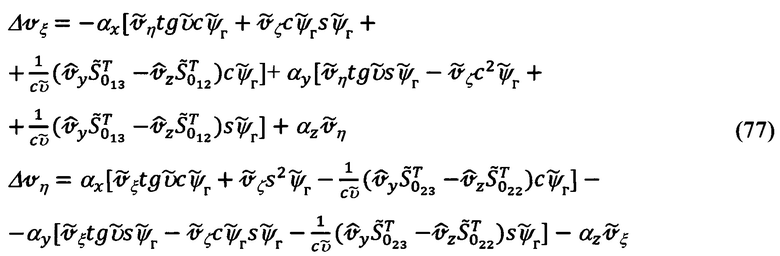
С учетом обозначений вида:
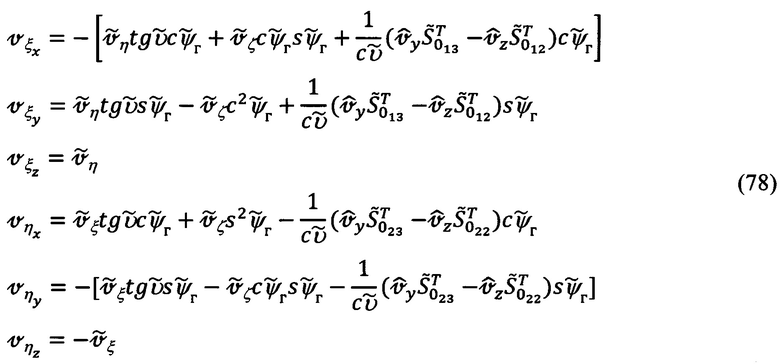
выражения для 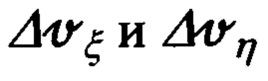 (77) можно представить в следующем компактном виде:
(77) можно представить в следующем компактном виде:

С целью формирования выражений для кинематических составляющих ΔVξ, ΔVη скорости, входящих в (70), (72), целесообразно привести дифференциальные уравнения, описывающие характер изменения координат Δξ, Δη, Δζ местоположения ИНС относительно ОПС в проекциях на оси ОТГП Oξηζ.
Из простых физических соображений можно показать, что указанные уравнения, а заодно и выражения для ΔVξ, ΔVη, ΔVζ, имеют вид:

где 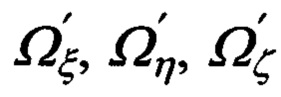 - составляющие угловой скорости объекта относительно ОТГП ИНС Oξηζ.
- составляющие угловой скорости объекта относительно ОТГП ИНС Oξηζ.
Параметры Δξ, Δη, Δζ, наряду с традиционными для ИНС параметрами, входят в перечень оцениваемых параметров состояния ИНС.
Приведем полный вектор XT ее параметров состояния:
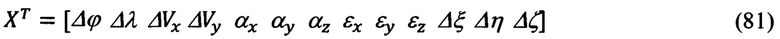
где εx, εy, εz - нескомпенсированные составляющие систематического ухода гиростабилизированной платформы ИНС.
В соответствии с уравнениями связи (72), выражениями для 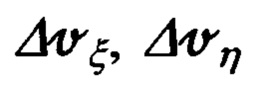 (79), дифференциальными уравнениями/выражениями (80) и видом вектора параметров состояния ИНС (81), скоростная часть матрицы наблюдения для рассматриваемой процедуры оптимального оценивания ошибок ИНС может быть представлена в виде:
(79), дифференциальными уравнениями/выражениями (80) и видом вектора параметров состояния ИНС (81), скоростная часть матрицы наблюдения для рассматриваемой процедуры оптимального оценивания ошибок ИНС может быть представлена в виде:
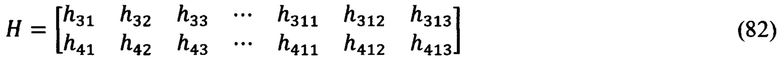
с элементами h3j, h4j (j=1÷13), равными:

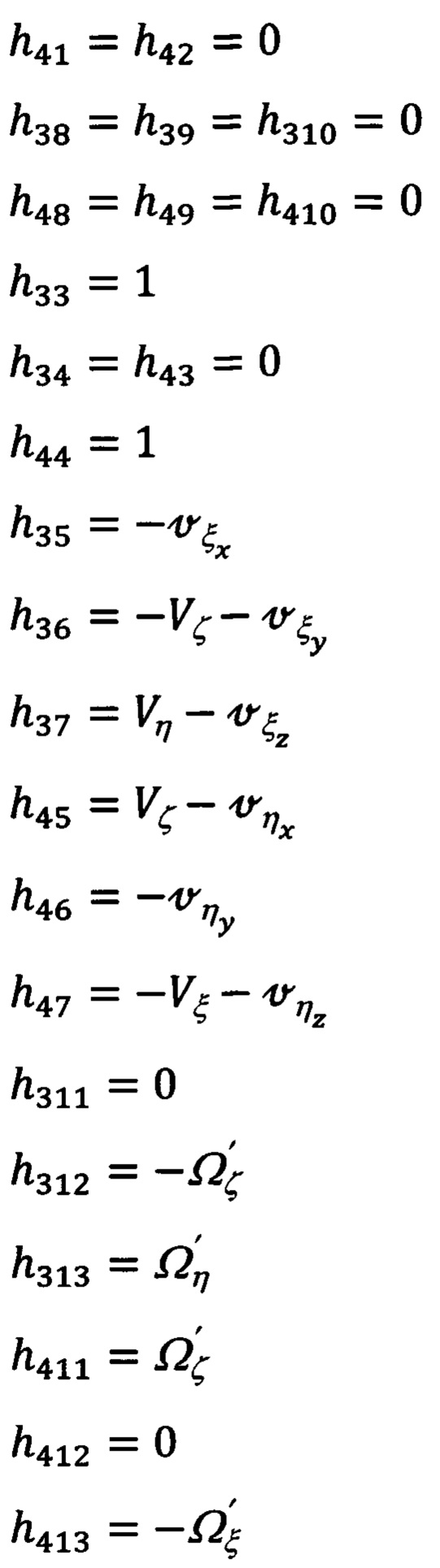
Выше показано, что используемый в предлагаемом изобретении подход, основанный на использовании кинематических соотношений связи ошибок Δψг, Δυ, Δγ измерения углов эволюции объекта с малыми углами αх, αу, αz ухода реальной ГП ИНС (61), при ошибочно измеренных скоростных сигналах измерения (73), а это, действительно, так, поскольку составляющие 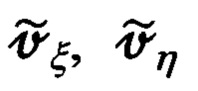 скорости, используемые в качестве сигналов измерителя (67) сформированы с ошибками
скорости, используемые в качестве сигналов измерителя (67) сформированы с ошибками 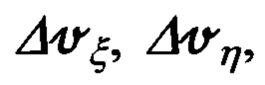 характер которых известен и описан выражениями (68), (74), (75)-(77), (79), позволяет через матрицу наблюдения (82), (83) учесть все ошибки сформированных по измерениям ОПС составляющих
характер которых известен и описан выражениями (68), (74), (75)-(77), (79), позволяет через матрицу наблюдения (82), (83) учесть все ошибки сформированных по измерениям ОПС составляющих 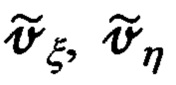 абсолютной линейной скорости объекта и тем самым обеспечить эффективное оценивание всех, зависящих от рассматриваемых измерений (73), параметров состояния ИНС, причем без ущерба для точности ее коррекции.
абсолютной линейной скорости объекта и тем самым обеспечить эффективное оценивание всех, зависящих от рассматриваемых измерений (73), параметров состояния ИНС, причем без ущерба для точности ее коррекции.
В качестве основного варианта расчета географических координат текущего местоположения объекта, предлагается метод, основанный на приведении оцененных компонент 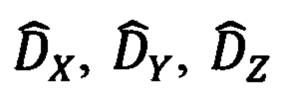 дальности до ОК к осям ССК Oxyz (30) и далее к осям ГСТ ONHE (27) с последующим преобразованием полученных в общем случае, ошибочных линейных компонент дальности
дальности до ОК к осям ССК Oxyz (30) и далее к осям ГСТ ONHE (27) с последующим преобразованием полученных в общем случае, ошибочных линейных компонент дальности 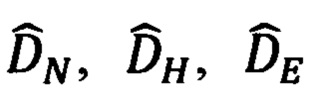 в некоторые угловые составляющие
в некоторые угловые составляющие 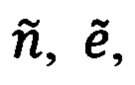 соответствующие широтно-долготной сетке в точке текущего местоположения объекта.
соответствующие широтно-долготной сетке в точке текущего местоположения объекта.
В соответствии с векторно-матричным выражением (27) и видом используемой в нем матрицы 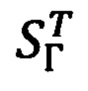 (29), запишем скалярные выражения для составляющих
(29), запишем скалярные выражения для составляющих 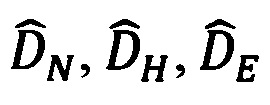 дальности до ориентира коррекции в проекциях на оси ГСТ ONHE:
дальности до ориентира коррекции в проекциях на оси ГСТ ONHE:
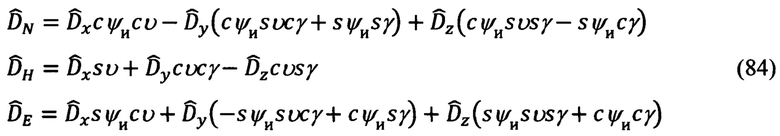
При действительных углах эволюции объекта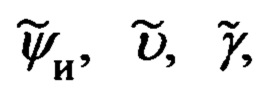 измеряемых с ошибками Δψи, Δυ, Δγ.
измеряемых с ошибками Δψи, Δυ, Δγ.

выражения для их истинных значений будут определяться соотношениями (59).
Подставка (59) в (84) позволяет получить выражения для идеальных компонент 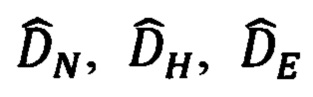 дальности до ОК, как разности ошибочно рассчитанных компонент
дальности до ОК, как разности ошибочно рассчитанных компонент 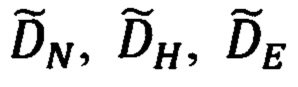 дальности и соответствующих ошибок ΔDN, ΔDH, ΔDE их расчета, обусловленных ошибками Δψи, Δυ, Δγ измерения углов эволюции объекта:
дальности и соответствующих ошибок ΔDN, ΔDH, ΔDE их расчета, обусловленных ошибками Δψи, Δυ, Δγ измерения углов эволюции объекта:

Для получения искомых выражений для 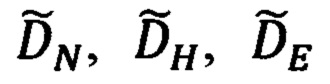 и ΔDN, ΔDH, ΔDE последовательно проведем описанные выше преобразования выражений (84).
и ΔDN, ΔDH, ΔDE последовательно проведем описанные выше преобразования выражений (84).
Подставляя (59) в (84), получим следующие выражения для компонент 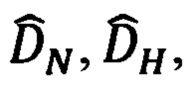
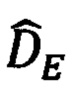 дальности до ОК в функции измеренных углов
дальности до ОК в функции измеренных углов 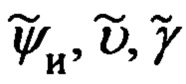 эволюции объекта и ошибок Δψи, Δυ, Δγ их измерения:
эволюции объекта и ошибок Δψи, Δυ, Δγ их измерения:
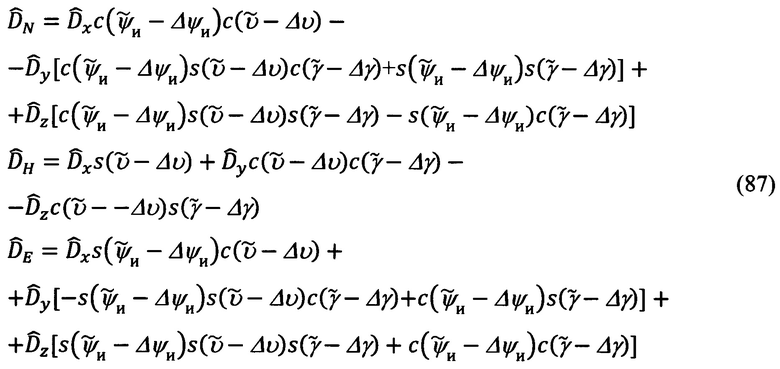
После раскрытия синусов и косинусов соответствующих углов и выполнения всех необходимых для получения выражений вида (86) преобразований, пренебрегая при этом величинами 2-го и более порядка малости относительно Δψи, Δυ, Δγ, получим следующие промежуточные выражения:
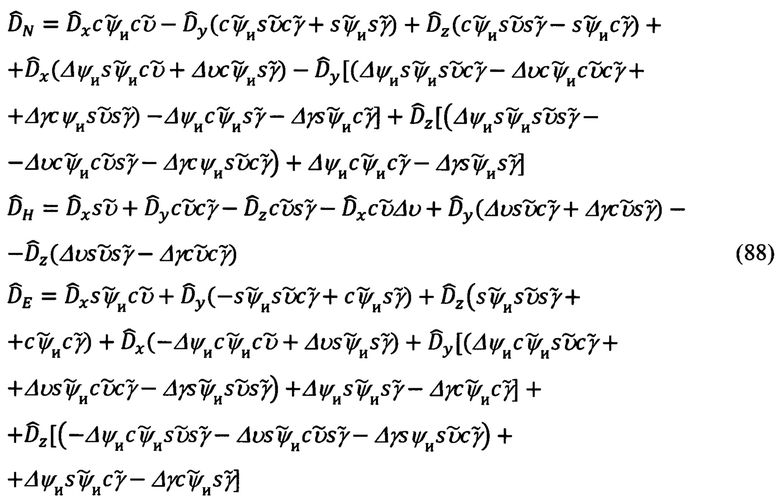
Понимая под 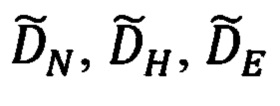 расчетные значения линейных компонент дальности до ОК, определяемые, исключительно, измеряемыми углами
расчетные значения линейных компонент дальности до ОК, определяемые, исключительно, измеряемыми углами  эволюции объекта, а под ΔDN, ΔDH, ΔDE - соответствующие погрешности их расчета, определяемые ошибками Δψи, Δυ, Δγ измерения углов эволюции объекта, в соответствии с (86) и на основании (88), запишем выражения для рассматриваемых компонент дальности:
эволюции объекта, а под ΔDN, ΔDH, ΔDE - соответствующие погрешности их расчета, определяемые ошибками Δψи, Δυ, Δγ измерения углов эволюции объекта, в соответствии с (86) и на основании (88), запишем выражения для рассматриваемых компонент дальности:
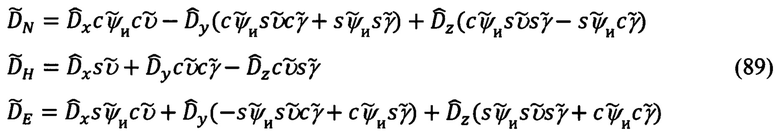

Учитывая, что в выражениях для ΔDN, ΔDH, ΔDE (90) будет осуществлена замена малых параметров Δψи, Δυ, Δγ на малые углы αх, αy, αz ухода реальной ГП ИНС, целесообразно все члены указанных выражений сгруппировать по ошибкам измерения текущих углов эволюции объекта.
После реализации указанной операции, выражения (90) примут вид:
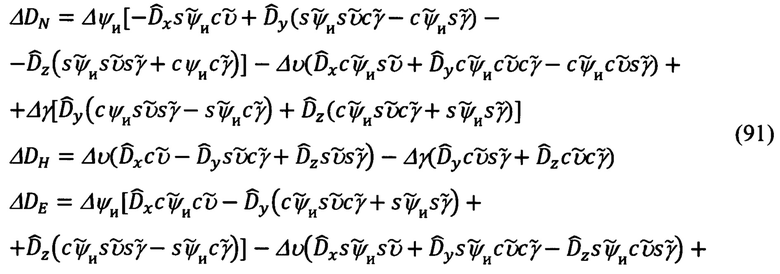
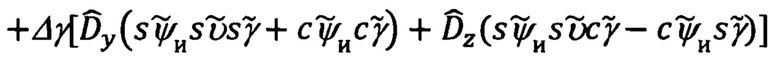
С учетом выражений для 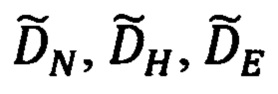 (89) и в соответствии с видом матрицы
(89) и в соответствии с видом матрицы 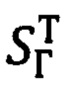 (29), полученные выражения для ΔDN, ΔDH, ΔDE (91) можно представить в следующем виде:
(29), полученные выражения для ΔDN, ΔDH, ΔDE (91) можно представить в следующем виде:
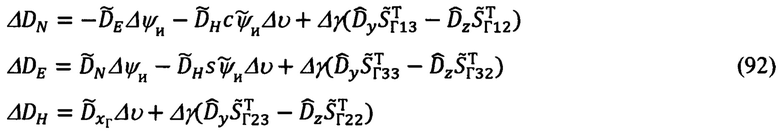
В приведенных выражениях (92) под 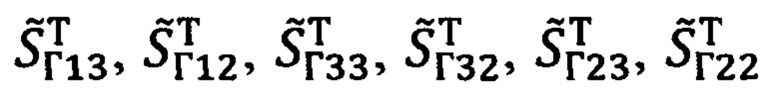 следует понимать соответствующие элементы матрицы
следует понимать соответствующие элементы матрицы 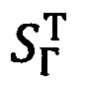 (29), а под
(29), а под 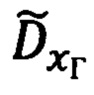 - расчетное значение горизонтированной дальности, которая, в соответствии с фиг. 6, равна:
- расчетное значение горизонтированной дальности, которая, в соответствии с фиг. 6, равна:

В дальнейшем выражение для ΔDH использовано не будет, поскольку оно имеет значение для синтеза вертикального канала ИНС, что не является предметом предлагаемого решения.
Представим такую гипотетическую ситуацию, что нам известны идеальные значения компонент 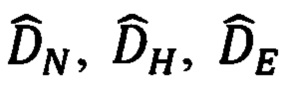 (86), (88) до ОК. Гипотетическую потому, что, в действительности, нам известны только расчетные компоненты
(86), (88) до ОК. Гипотетическую потому, что, в действительности, нам известны только расчетные компоненты 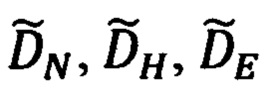 дальности (89).
дальности (89).
Используя, указанные значения идеальных компонент 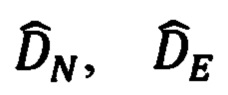 (86) горизонтированной дальности, в соответствии с известными выражениями могут быть рассчитаны соответствующие им идеальные приращения
(86) горизонтированной дальности, в соответствии с известными выражениями могут быть рассчитаны соответствующие им идеальные приращения 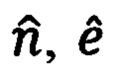 географических координат текущего местоположения объекта относительно ОК. Приведем их:
географических координат текущего местоположения объекта относительно ОК. Приведем их:

где RN, RE - главные радиусы кривизны земного эллипсоида вращения:
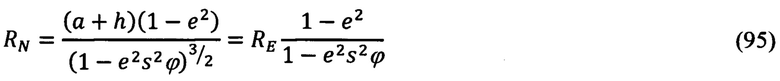

где а - большая полуось земного эллипсоида вращения; h - высота над уровнем моря; е2 - квадрат первого эксцентриситета:
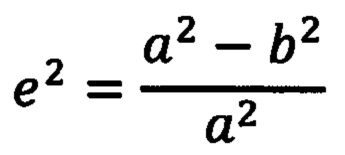
b - малая полуось земного эллипсоида вращения.
При расчете RN, RE целесообразно использовать бароинерциальную высоту, а в качестве географической широты ϕ и долготы λ - их идеальные значения, представленные соотношениями (1.10) в функции счисленных ИНС 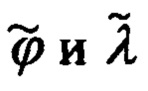 и ошибок Δϕ и Δλ их счисления.
и ошибок Δϕ и Δλ их счисления.
Прежде, чем представлять выражения (94) в целесообразном для их дальнейшего использования виде, преобразуем приведенные выше выражения (95) для расчета главных радиусов кривизны RN, RE.
Учитывая, что параметр e2s2ϕ является малым и во всем диапазоне изменения географической широты не превышает принятого для эллипсоида Ф.Н. Красовского значения равного 0,0066934 (1946 г.), представляется целесообразным с достаточной для синтеза рассматриваемого способа оптимального оценивания и коррекции точностью выражения (95) для расчета главных радиусов RN, RE кривизны земного эллипсоида вращения записать в виде:
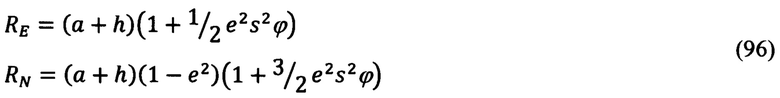
Подставляя в (96) вместо географической широты ее представление в функции счисленной широты 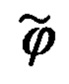 и погрешности Δϕ ее счисления (1.10), с точностью до величины первого порядка малости относительно Δϕ получим следующие выражения для RN, RE:
и погрешности Δϕ ее счисления (1.10), с точностью до величины первого порядка малости относительно Δϕ получим следующие выражения для RN, RE:
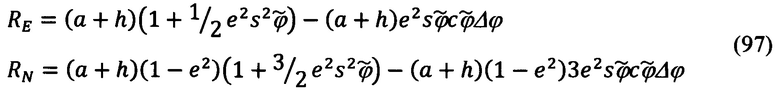
Очевидно, что выражения (97) могут быть представлены в традиционном для проводимого исследования виде:

где выражения для 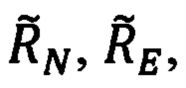 ΔRN, ΔRE, в соответствии с (97), имеют вид:
ΔRN, ΔRE, в соответствии с (97), имеют вид:
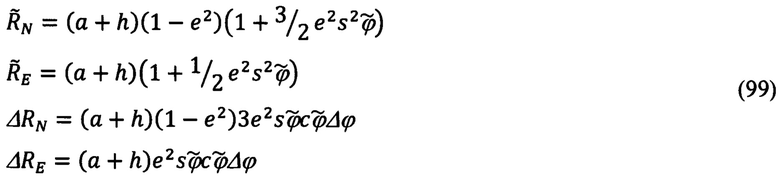
Расписывая выражения (94) с учетом (98) и 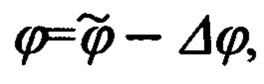 получим следующие выражения для идеальных значений
получим следующие выражения для идеальных значений 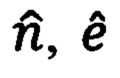 отклонения объекта по широте и долготе относительно ориентира коррекции:
отклонения объекта по широте и долготе относительно ориентира коррекции:
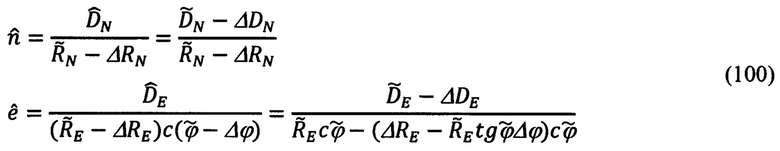
Вводя для величины 1-го порядка малости относительно Δϕ и ΔRE, входящей в знаменатель выражения для 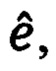 обозначение вида:
обозначение вида:

получим следующее выражение для 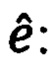

Подставляя в выражение для 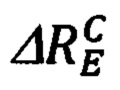 значения для ΔRE и
значения для ΔRE и 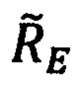 (99), получим его следующее представление:
(99), получим его следующее представление:
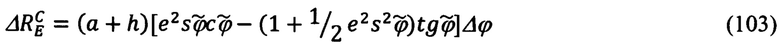
Раскладывая приведенные выше выражения для 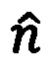 (100) и
(100) и 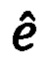 (102) в ряд Тейлора в окрестности измеренных значений
(102) в ряд Тейлора в окрестности измеренных значений 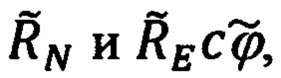 ограничиваясь при этом линейными членами разложения, получим следующие выражения для
ограничиваясь при этом линейными членами разложения, получим следующие выражения для 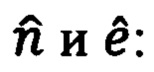

Подстановка в (104) выражений для  (86) приводит, с точностью до величин первого порядка малости относительно ΔDE, ΔDN,
(86) приводит, с точностью до величин первого порядка малости относительно ΔDE, ΔDN, 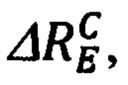 ΔRN, к выражениям вида:
ΔRN, к выражениям вида:

Выражения (105) целесообразно записать в традиционном для них виде, а именно:

где 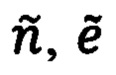 - расчетные значения угловых координат положения объекта относительно ОК; Δn, Δе - соответствующие ошибки их расчета, определяемые выражениями:
- расчетные значения угловых координат положения объекта относительно ОК; Δn, Δе - соответствующие ошибки их расчета, определяемые выражениями:
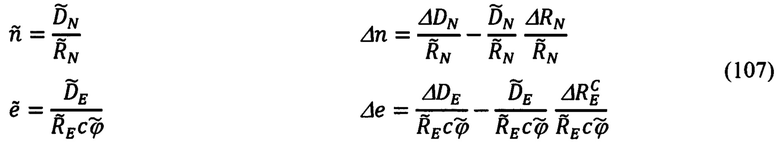
На основании простых физических соображений можно показать, что при абсолютно точных координатах OK (ϕ0, λ0), координаты текущего местоположения объекта будут равны:

Приведенных выражениях 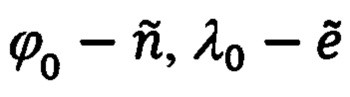 - это расчетные значения координат местоположения объекта. Обозначая их через
- это расчетные значения координат местоположения объекта. Обозначая их через 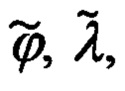 запишем следующие выражения для их идеальных значений (108):
запишем следующие выражения для их идеальных значений (108):

Иначе, приведенные выражения можно записать в виде:

Счисленные инерциальной навигационной системой координаты текущего местоположения объекта целесообразно описать выражениями вида:

где Δϕ, Δλ - ошибки инерциального счисления, Δϕk, Δλk - смещения координат местоположения ИНС относительно ОПС. Сравнение соответствующих координат текущего местоположения объекта, счисленных ИНС (111) и сформированных по результатам визирования ОК с использованием ОПС (110), приводит к следующим уравнениям связи:

Принимая левые части полученных уравнений связи в качестве позиционных сигналов измерения:

по их правым частям, в соответствии с представленным выше вектором параметров состояния ИНС (81), формируют соответствующие элементы матрицы наблюдения. Но для этого необходимо, чтобы входящие в правую часть уравнений связи (112) компоненты Δϕk, Δλk, Δn, Δе были представлены в функции соответствующих параметров состояния ИНС, оцениваемых в процессе оптимальной фильтрации и идентификации. В рассматриваемом случае коррекции это означает их зависимость от таких параметров состояния, как Δϕ, Δλ, Δξ, Δη, αx, αу (80), (81).
Полученные выше выражения (92), определяющие характер изменения составляющих ΔDN, ΔDH, ΔDE представлены в функции ошибок Δψи, Δυ, Δγ измерения углов 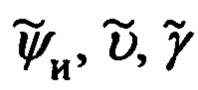 эволюции объекта.
эволюции объекта.
Для представления выражений для ΔDN и ΔDE, а, следовательно, Δn иΔе, в функции таких параметров состояния, как Δλ, αx, αy, необходимо в выражения (92) вместо Δψи, Δυ, Δγ подставить их значения, определяемые кинематическими соотношениями связи Δψи, Δυ, Δγ и Δχ, Δϕ, Δλ с малыми углами рассогласования реального и опорного трехгранников ГП ИНС (61) и (60).
Учитывая, что по определению:

поэтому, подставляя в (114) выражения для Δχ (60) и Δψг (61), получим следующее выражение для Δψи:

После подстановки кинематических соотношений, определяющих Δυ, Δγ (61) и Δψи (115), в выражения для ΔDN и ΔDE (92) получим их представление в функции αx, αу, Δλ:
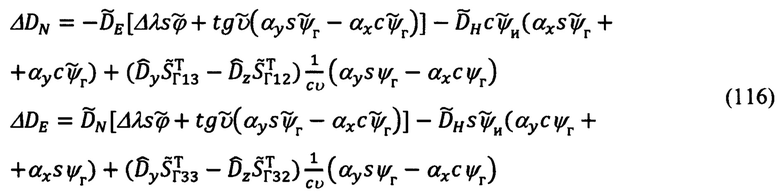
Приводя в (116) подобные члены, группируя их по параметрам состояния αx, αy, Δλ, запишем их в следующем виде:
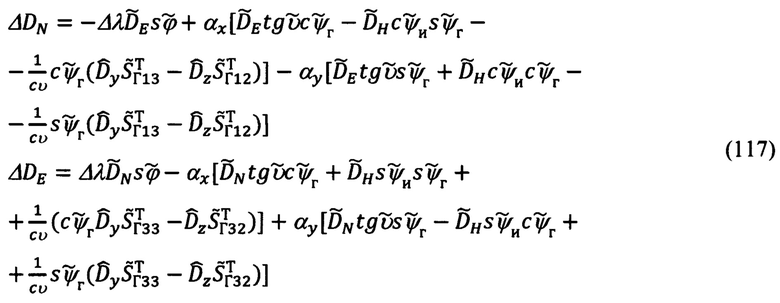
Введем следующие обозначения для коэффициентов при αx, αу, Δλ:
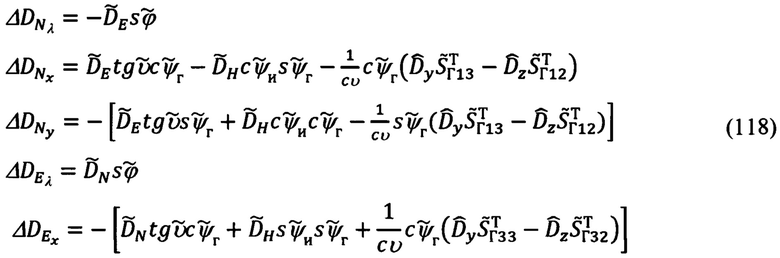
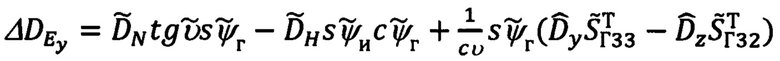
С учетом введенных обозначений выражения для ΔDN и ΔDE (117) можно записать в следующем виде:

В соответствии с (107) и (119), выражения для ошибок Δn и Δе расчета значений угловых координат 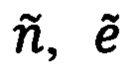 положения объекта относительно ориентира коррекции могут быть представлены в следующем развернутом виде:
положения объекта относительно ориентира коррекции могут быть представлены в следующем развернутом виде:
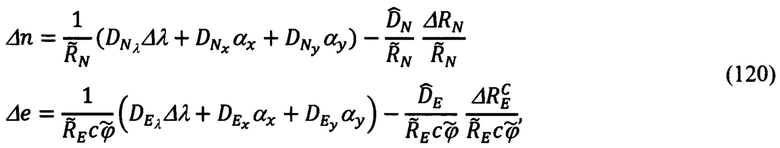
где 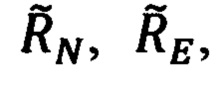 ΔRN, ΔRE,
ΔRN, ΔRE,  определяются выражениями (99), (101),
определяются выражениями (99), (101), 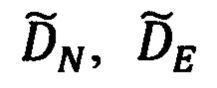 - выражениями (89), а
- выражениями (89), а 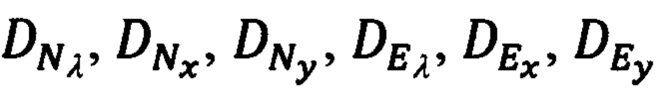 - полученными выше выражениями (118).
- полученными выше выражениями (118).
Представляя выражения для 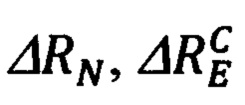 (99), (101), в виде:
(99), (101), в виде:

где А и В, в соответствии с (99) и (101) определяются, как:

выражения (120) записывают следующим образом:

где 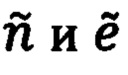 определены выше (107).
определены выше (107).
Выше приведены также дифференциальные уравнения (80), описывающие характер изменения координат Δξ, Δη, Δζ местоположения (размещения на объекте) ИНС относительно ОПС в проекциях на оси ОТГП ИНС Oξηζ.
При известных оценках 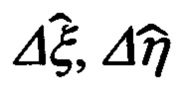 указанных координат достаточно просто могут быть сформированы конструктивные компоненты Δϕk, Δλk, входящие в полученные выше уравнения связи (112) для позиционных сигналов:
указанных координат достаточно просто могут быть сформированы конструктивные компоненты Δϕk, Δλk, входящие в полученные выше уравнения связи (112) для позиционных сигналов:

После определения всех параметров правых частей полученных выше уравнений связи (112) приведем аналитическое представление для позиционных элементов матрицы наблюдения Н, а именно, ее первую и вторую строки:
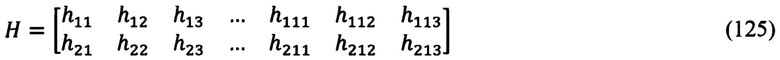
Элементы h1j, h2j (j=1÷13) рассматриваемой матрицы наблюдения, в соответствии с (81), (112), (123) и (124), будут иметь следующий вид:
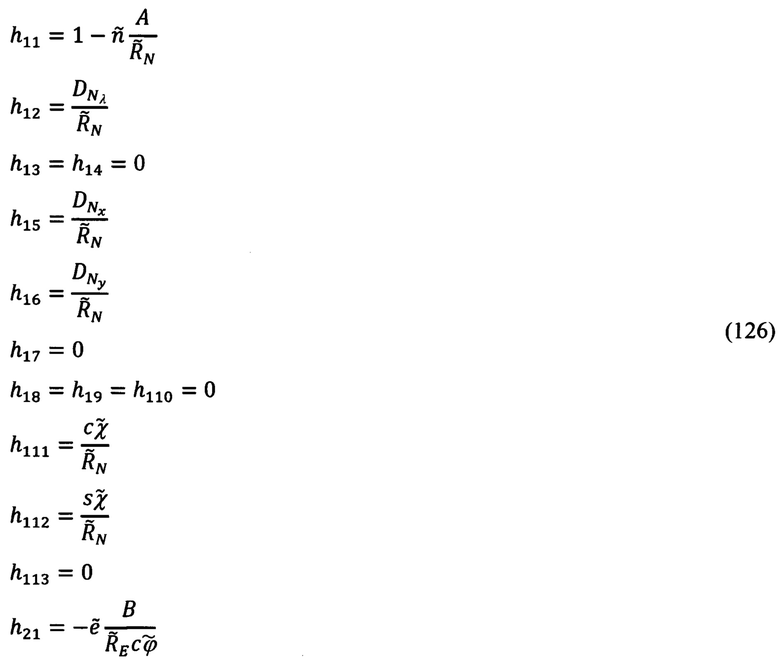
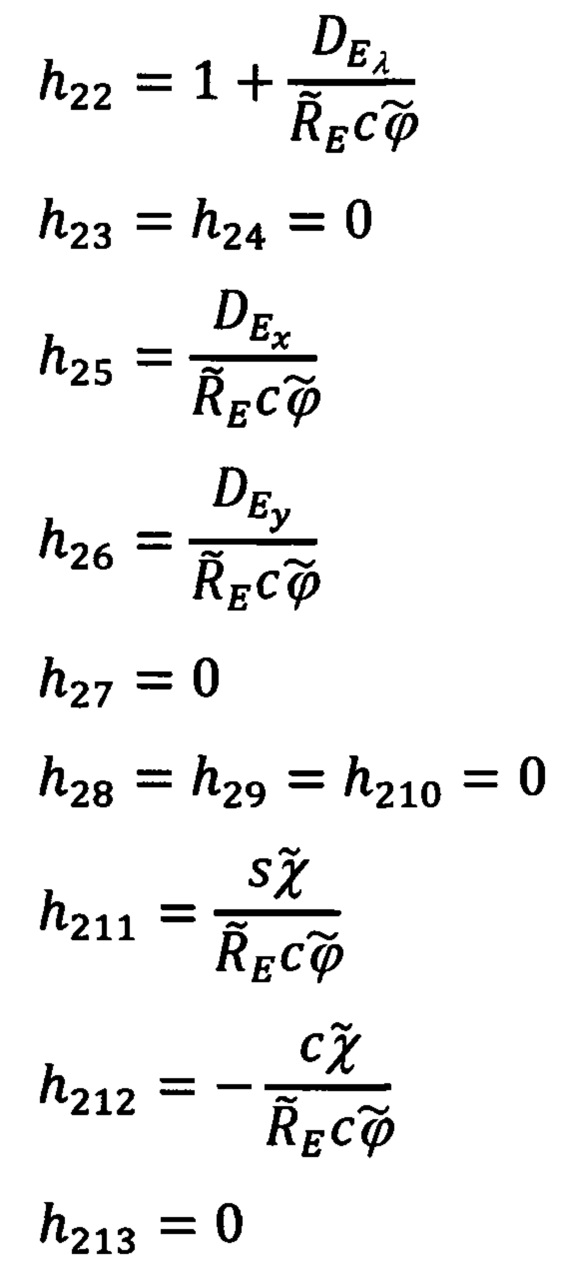
Таким образом, располагая ошибочными координатами текущего местоположения объекта (110) и используя их в качестве сигналов измерителя ошибочно счисляемых инерциальных координат (111), можно реализовать гарантированно эффективное по точности и быстродействию оценивание всех параметров состояния ИНС, долгосрочный прогноз и коррекцию счисляемых и измеряемых ею сигналов.
Аналогичный вывод сделан выше и относительно скоростных сигналов измерения.
Учитывая, что приведенные выше дифференциальные уравнения (47), (48), (49) описывающие характер движения объекта относительно ориентира коррекции, модифицированы и отличаются от их исходного аналога (39), (40), (41), представляется целесообразным процедуру оптимального оценивания компонент DX, DY, DZ дальности и ошибок 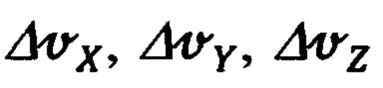 (46) измерения инерциальной системой составляющих
(46) измерения инерциальной системой составляющих 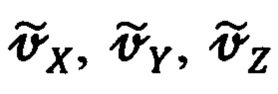 абсолютной линейной скорости объекта расписать более подробно.
абсолютной линейной скорости объекта расписать более подробно.
В соответствии с поканально представленной системой дифференциальных уравнений (47), (48), (49) дискретная модель сообщения рассматриваемой системы в терминах оптимальной фильтрации (52)-(58) имеет вид:
1. Канал X
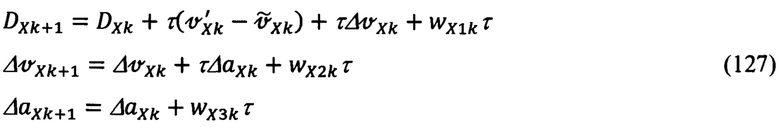
2. Канал Y
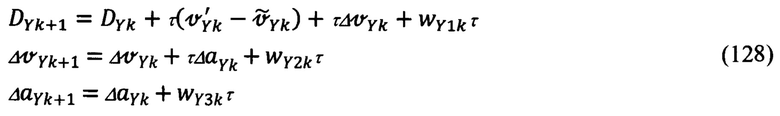
3. Канал Z
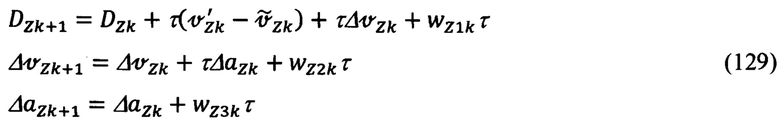
где wXik, wYik, wZik (i=1-3) - белые шумы возмущений, действующих в каждом из каналов; τ - дискретность вычислений.
В соответствии с (127)-(129) фундаментальные матрицы для каналов X, Y и Z будут иметь вид:

Матрицы ГXk+1,k, ГYk+1,k, ГZk+1,k передачи случайных возмущений wXik, wYik, wZik, очевидно, будут равны:
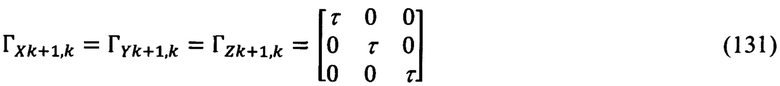
Корреляционные матрицы QX, QY, QZ возмущающих шумов модели сообщения представим в следующем виде:
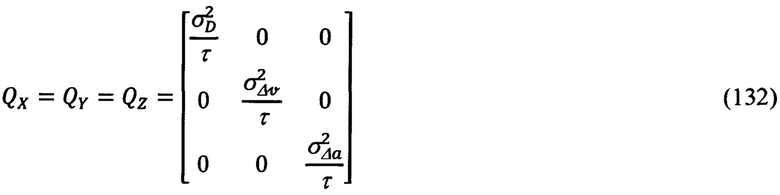
где 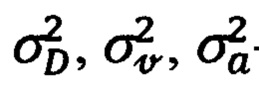 - дисперсии возмущающих шумов по дальности, скорости и ускорению соответственно.
- дисперсии возмущающих шумов по дальности, скорости и ускорению соответственно.
Матрицы измерения НХ, HY, HZ, учитывая, что векторы параметров состояния для каждого из каналов имеют вид:
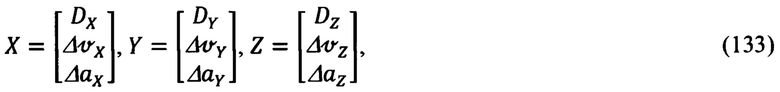
будут равны:

Корреляционные матрицы RX, RY, RZ шумов измерения равны:

где σ2 - дисперсия измерительных шумов в каждом тракте измерения компонент дальности.
Матрицы оптимальных коэффициентов усиления для каждого из рассматриваемых каналов будут иметь вид:
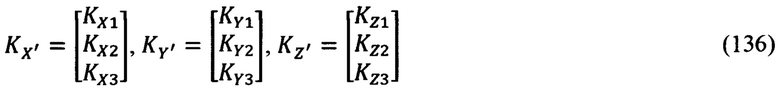
Процедура расчета указанных матриц является традиционной и осуществляется в соответствии с матричным выражением (56).
В соответствии с (55) выражения для расчета апостериорных оценок будут иметь вид:
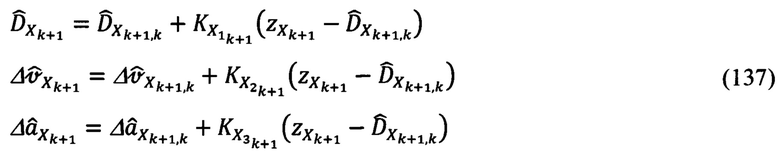
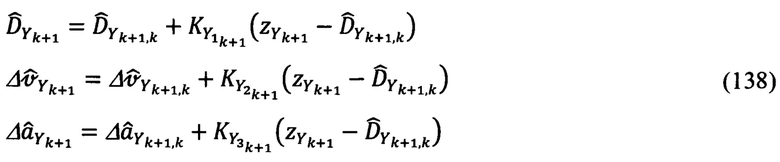
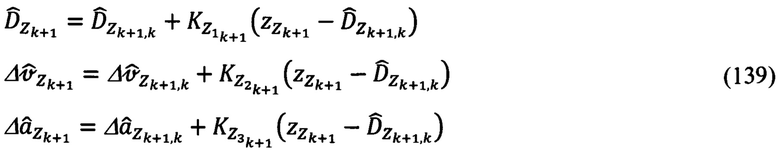
В приведенных уравнениях компоненты с индексами k+1,k - априорные оценки соответствующих параметров состояния системы. Выражения для их расчета, в соответствии с (127)-(128), будут равны:
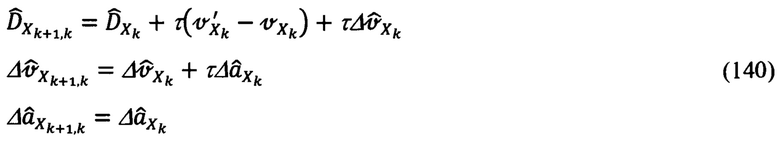
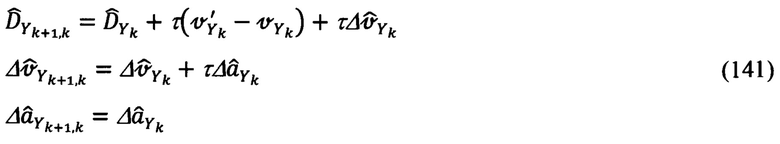
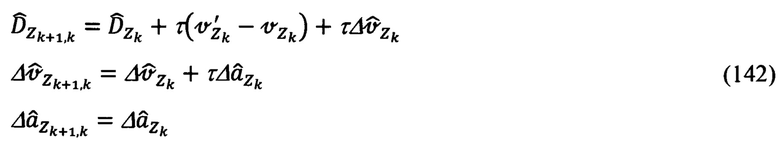
Полученные в процессе оптимального оценивания оценки 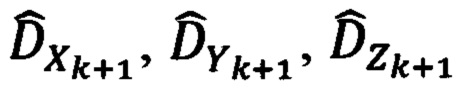 компонент дальности до ОК используют в соответствии с представленным выше описанием, а расчет идеальных составляющих абсолютной линейной скорости объекта осуществляют в соответствии с выражениями (46), используя при этом вместо
компонент дальности до ОК используют в соответствии с представленным выше описанием, а расчет идеальных составляющих абсолютной линейной скорости объекта осуществляют в соответствии с выражениями (46), используя при этом вместо 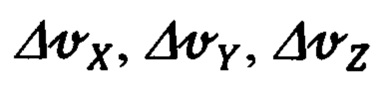 их оценки
их оценки 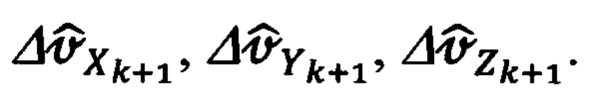
Модифицированная процедура формирования дальности до ориентира коррекции используется при фильтрации компонент дальности до ОК и оптимальном оценивании скоростных погрешностей инерциальной системы и предназначена для заполнения одно-двух секундных временных интервалов между соседними измерениями дальности (интервалы росдыха ЛД) ее десяти герцовыми расчетными значениями.
Указанный вариант целесообразен при необходимости измерения дальности на достаточно протяженных временных интервалах, составляющих единицы минут, когда ЛД, как правило, работает в щадящем для него режиме с частотой излучающих посылок не выше 0,5-1,0 Гц.
При решении высокотехнологичных задач, предполагающих использование процедуры оптимальной фильтрации и идентификации, приемлемой частотой обработки информации является 10 Гц.
Рассматриваемая задача коррекции предполагает реализацию одновременно двух процедур оптимального оценивания, а именно, фильтрации компонент дальности до ОК и оценивания составляющих абсолютной линейной скорости объекта, которая является вспомогательной процедурой, и основной, связанной с оцениванием частных ошибок инерциальной системы и коррекцией ее выходных сигналов.
Суть предлагаемой модифицированной процедуры формирования наклонной дальности состоит в следующем.
Каждое измеренное значение наклонной дальности до ОК, помимо его использования в соответствии с представленным выше описанием, дополнительно используют для расчета текущего опорного - до следующего измерения дальности, значения высоты цели над уровнем моря Δh0 или иначе бароинерциальной высоты ОК.
Для этого по измеренному - опорному значению дальности 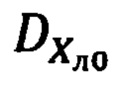 и соответствующего указанному моменту времени значению косинуса с θ0 угла между векторами географической вертикали и направлением на ОК определяют геометрическую высоту h0 объекта относительно цели:
и соответствующего указанному моменту времени значению косинуса с θ0 угла между векторами географической вертикали и направлением на ОК определяют геометрическую высоту h0 объекта относительно цели:

Сравнивая указанное значение высоты с текущей бароинерциальной высотой 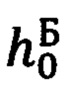 объекта, получают искомое - опорное значение высоты Δh0 ОК над уровнем моря:
объекта, получают искомое - опорное значение высоты Δh0 ОК над уровнем моря:

Далее полученное значение высоты (144) используют на одно или двух секундном интервале росдыха ЛД для формирования 10-ти герцовых расчетных значений дальности.
Для чего, в каждый последующий, после измерения опорной дальности такт решения рассматриваемой задачи по текущему значению бароинерциальной высоты 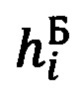 объекта и известной опорной высоте ОК над уровнем моря Δh0 (144) определяют текущее значение геометрической высоты объекта относительно ОК:
объекта и известной опорной высоте ОК над уровнем моря Δh0 (144) определяют текущее значение геометрической высоты объекта относительно ОК:

Искомое значение текущей наклонной дальности определяют в соответствии с выражением вида:

где текущее значение с θi (i=0, 1, …, 9/19) (143), (146) определяют в соответствии с выражением:
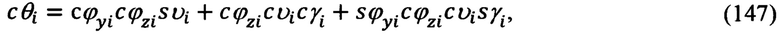
которое рассчитывают с частотой 10 Гц.
По окончании активной фазы оптимального оценивания ошибок автономного инерциального счисления, основанного на рекуррентной процедуре обработки, фильтрации и идентификации постоянно обновляющейся входной последовательности сигналов, формируемых по измерениям ИНС и вспомогательной процедуры оптимального оценивания, фильтр-идентификатор ошибок ИНС переводят в режим долгосрочного, до следующего сеанса оценивания, прогноза полученных оценок. При этом коррекция измеряемой ИНС навигационной и пилотажной информации осуществляется как в процессе оптимального оценивания, так и прогноза.
Особенностью работы фильтра-идентификатора ошибок ИНС в режиме прогноза является обнуление входных сигналов фильтра и приостановка математической процедуры расчета оптимальных коэффициентов усиления, которые на все время прогноза принимаются равными нулю.
В качестве начальных значений оценок в процедуре прогноза используют их значения, полученные по завершении оптимального оценивания, при этом все значения передаточных коэффициентов, взвешивающих рассматриваемые оценки, рассчитываются в соответствии с их аналитическим представлением в расширенной модели ошибок ИНС.
Далее, при описании процедуры коррекции инерциальной информации полученные в результате прогноза значения оценок будем обозначать по аналогии с оптимальными оценками, а именно ,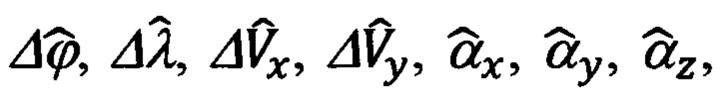 …, а счисленные значения инерциальных параметров, как
…, а счисленные значения инерциальных параметров, как 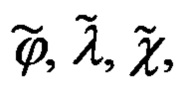 Vx, Vy, …
Vx, Vy, …
Приведем процедуру коррекции основных навигационных и пилотажных параметров.
Коррекцию горизонтальных составляющих Vx, Vy абсолютной линейной скорости объекта, представленных в виде (69), осуществляют в соответствии с выражениями:

Очевидно, что зная счисленные значения составляющих Vx, Vy абсолютной линейной скорости объекта и текущие оцененные или спрогнозированные значения оценок 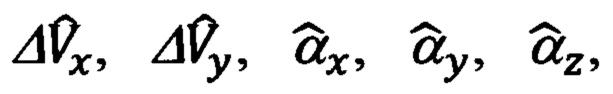 а также бароинерциальную составляющую Vζ вертикальной скорости, в соответствии с выражениями (148), с точностью до величин первого порядка малости относительно
а также бароинерциальную составляющую Vζ вертикальной скорости, в соответствии с выражениями (148), с точностью до величин первого порядка малости относительно 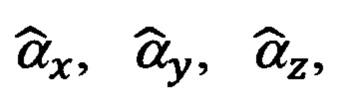 могут быть рассчитаны откорректированные составляющие
могут быть рассчитаны откорректированные составляющие 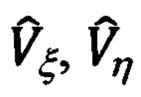 абсолютной скорости.
абсолютной скорости.
При коррекции географических координат местоположения объекта и его истинного курса будем считать, что счисленные значения координат 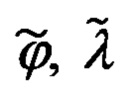 и угла
и угла 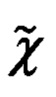 азимутальной ориентации опорного трехгранника гироплатформы ИНС определяются выражениями вида (1.10), а именно:
азимутальной ориентации опорного трехгранника гироплатформы ИНС определяются выражениями вида (1.10), а именно:

где ϕ, λ, Δχ - идеальные значения рассматриваемых параметров, Δϕ, Δλ, Δχ - ошибки их счисления.
Следовательно, располагая текущими значениями оценок 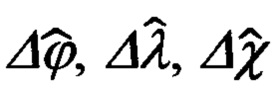 ошибок счисления указанных параметров, достаточно просто могут быть рассчитаны их откорректированные значения
ошибок счисления указанных параметров, достаточно просто могут быть рассчитаны их откорректированные значения 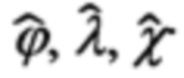 :
:

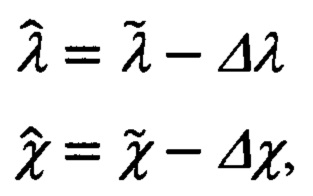
При этом оценка 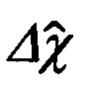 рассчитывается в соответствии с кинематическим соотношением вида (61):
рассчитывается в соответствии с кинематическим соотношением вида (61):

где 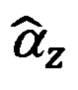 - оценка курсового ухода гироплатформы ИНС.
- оценка курсового ухода гироплатформы ИНС.
При коррекции истинного курса объекта воспользуемся выражением, в соответствии с которым осуществляется его расчет:

Очевидно, что в вариациях это выражение будет иметь вид:

из которого следует, что погрешность Δψи формирования истинного курса ψи определяется ошибкой Δχ счисления угла χ азимутальной ориентации опорного трехгранника ГП ИНС и ошибкой Δψг измерения гироскопического курса ψг.
Воспользовавшись соответствующими кинематическими соотношениями для Δχ (60) и Δψг (61), запишем выражения для Δψи (153) в следующем виде:

С учетом соотношения для Δγ (61) его можно представить в следующем алгоритмически целесообразном виде:
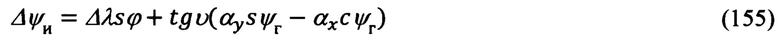
Из полученного выражения следует, что погрешность Δψи формирования истинного курса ψи не зависит от угла αz азимутального ухода ГП ИНС.
Таким образом, располагая оцененными или спрогнозированными значениями оценок 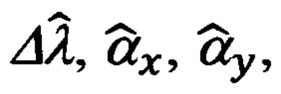 счисленным значением географической широты
счисленным значением географической широты 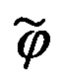 и измренными значениями тангажа
и измренными значениями тангажа 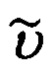 и гироскопического курса
и гироскопического курса 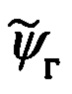 объекта, может быть определена оценка
объекта, может быть определена оценка 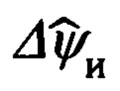 погрешности формирования истинного курса:
погрешности формирования истинного курса:
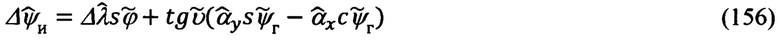
При этом откорректированное значение самого курса 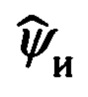 может быть определено в соответствии с выражением вида:
может быть определено в соответствии с выражением вида:

Процедура коррекции всех пилотажных параметров, а именно, углов гироскопического курса ψг, крена γ и тангажа υ объекта предполагает использование кинематических соотношений (61).
Действительно, зная текущие значения оценок малых углов 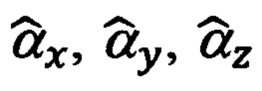 ухода реальной ГП ИНС, в соответствии с первым выражением системы (61), определяют оценку
ухода реальной ГП ИНС, в соответствии с первым выражением системы (61), определяют оценку 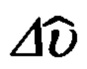 ошибки измерения угла тангажа объекта:
ошибки измерения угла тангажа объекта:

зная которую на рассматриваемом такте вычисления рассчитывают откорректированное значение тангажа 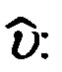

На этом же такте, зная уже откорректированное значение тангажа  в соответствии со 2-ым соотношением системы (61) определяют оценку
в соответствии со 2-ым соотношением системы (61) определяют оценку 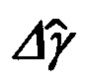 ошибки измерения крена
ошибки измерения крена 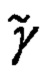 объекта:
объекта:

после чего на этом же такте определяют его откорректированное значение:

И последние операции рассматриваемого такта связаны с коррекцией гироскопического курса 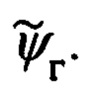
В соответствии с 3-им соотношением системы (61) формируют оценку 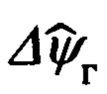 ошибки измерения
ошибки измерения 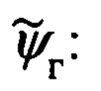

после чего, определяют откорректированное значение гироскопического курса 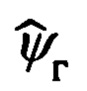 объекта:
объекта:

Способ оптимального оценивания ошибок инерциальной навигационной системы и ее коррекции по неподвижному ориентиру с известными географическими координатами реализуется следующим образом:
1. При полете относительно неподвижного наземного ориентира коррекции по предварительно согласованной траектории с непрерывным, в течение пяти-шести минут, его угловым сопровождением и дискретным измерением наклонной дальности до него в щадящем для лазерного дальномера из состава обзорно-прицельной системы режиме его работы - с частотой посылок, не превышающей 0,5-1,0 Гц, при этом все массивы текущей информации, измеряемой ОПС, ИНС и комплексным бароинерциальным каналом формирования абсолютной высоты и вертикальной скорости обрабатывают таким образом, чтобы обеспечить как эффективное оптимальное оценивание ошибок счисленных географических координат текущего местоположения объекта и измеряемых ИНС составляющих его абсолютной линейной скорости, так и формирование оценок ошибок углов текущей ориентации объекта с реализацией их долгосрочного, не превышающего 40-ка минут, прогноза и параллельной коррекции всего массива ее выходных параметров.
При этом, для достижения технического результата изобретения осуществляют:
2. В обеспечение разработки точной и эффективной процедуры оптимального оценивания горизонтальных составляющих 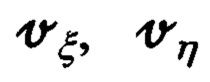 абсолютной линейной скорости объекта, используемых в качестве сигналов скоростного измерителя в основной процедуре оптимального оценивания ошибок ИНС, одно-двух секундные временные интервалы между соседними измерениями дальности (интервалы роздыха ЛД) заполняют 10-ти герцовыми расчетными значениями, которые формируют в соответствии с модифицированной, инвариантной к рельефу подстилающей поверхности, угломестной процедурой расчета наклонной дальности до ОК, реализуемой на основе использования текущей бароинерциальной высоты
абсолютной линейной скорости объекта, используемых в качестве сигналов скоростного измерителя в основной процедуре оптимального оценивания ошибок ИНС, одно-двух секундные временные интервалы между соседними измерениями дальности (интервалы роздыха ЛД) заполняют 10-ти герцовыми расчетными значениями, которые формируют в соответствии с модифицированной, инвариантной к рельефу подстилающей поверхности, угломестной процедурой расчета наклонной дальности до ОК, реализуемой на основе использования текущей бароинерциальной высоты 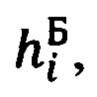 косинуса с θi угла между географической вертикалью и направлением на ОК и опорным 1-2-х герцовым значением высоты ОК над уровнем моря Δh0. Указанная процедура приведена в описании изобретения и представлена выражениями (143)-(147).
косинуса с θi угла между географической вертикалью и направлением на ОК и опорным 1-2-х герцовым значением высоты ОК над уровнем моря Δh0. Указанная процедура приведена в описании изобретения и представлена выражениями (143)-(147).
3. Кинематические дифференциальные уравнения движения объекта относительно ОК представляют в проекциях на оси ИСК, чем обеспечивают кардинальное упрощение описывающих его уравнений за счет реализации естественной поканальной декомпозиции модели их относительного движения, вследствие чего, вместо взаимосвязанной кинематической модели 9-го порядка, получают три структурно идентичных и не связанных между собой канала (36), (37), (38), на основе которых синтезируют три независимых, структурно и алгоритмически идентичных фильтра-идентификатора.
4. Учитывая, что в рассматриваемой задаче абсолютная линейная скорость ОК, может быть определена безошибочно (43), (44), дифференциальные уравнения относительного движения объекта (36)-(38) видоизменяют и представляют в виде (39)-(41), удобном для оптимального оценивания составляющих 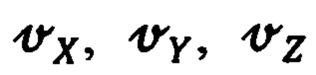 абсолютной линейной скорости объекта. После подстановки в них вместо составляющих
абсолютной линейной скорости объекта. После подстановки в них вместо составляющих 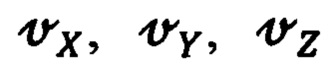 их значений, определяемых адекватными для них выражениями (46), переходят от уравнений для скорости и ускорения объекта в полных сигналах к уравнениям в вариациях, представленным в виде модифицированной системы дифференциальных уравнений (47)-(49), которую используют в процедуре оптимального оценивания ошибок
их значений, определяемых адекватными для них выражениями (46), переходят от уравнений для скорости и ускорения объекта в полных сигналах к уравнениям в вариациях, представленным в виде модифицированной системы дифференциальных уравнений (47)-(49), которую используют в процедуре оптимального оценивания ошибок 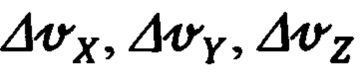 счисления составляющих
счисления составляющих 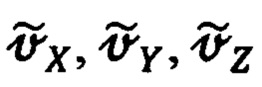 абсолютной линейной скорости. По известным счисленным значениям компонент
абсолютной линейной скорости. По известным счисленным значениям компонент 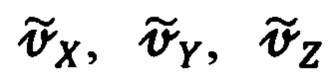 абсолютной линейной скорости объекта и оцененным ошибкам
абсолютной линейной скорости объекта и оцененным ошибкам 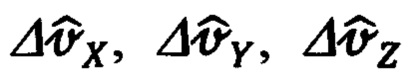 определения ее текущих составляющих, в соответствии с (51), формируют искомые значения оценок
определения ее текущих составляющих, в соответствии с (51), формируют искомые значения оценок 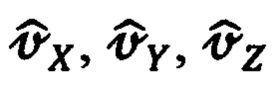 составляющих абсолютной линейной скорости.
составляющих абсолютной линейной скорости.
Процедура оптимального оценивания текущих компонент 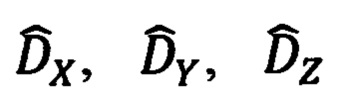 дальности и ошибок
дальности и ошибок 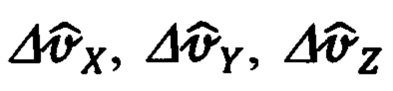 счисления абсолютной скорости и ускорения
счисления абсолютной скорости и ускорения  объекта представлена уравнениями/выражениями (127)-(142).
объекта представлена уравнениями/выражениями (127)-(142).
Пересчет составляющих (51) абсолютной линейной скорости объекта к осям ОТГП ИНС Oξηζ осуществляют в соответствии с векторно-матричным выражением, обратным (50). При этом, приведение отфильтрованных оценок компонент 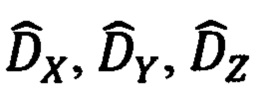 дальности до ОК к осям ГСТ ONHE реализуют в соответствии с выражением вида (32).
дальности до ОК к осям ГСТ ONHE реализуют в соответствии с выражением вида (32).
5. В соответствующем разделе осуществления изобретения на основе простых физических соображений, показано, что ошибки приведения оценок компонент 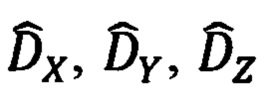 дальности до ОК к осям ГСТ ONHE определяются ошибками Δψи, Δυ, Δγ измерения углов
дальности до ОК к осям ГСТ ONHE определяются ошибками Δψи, Δυ, Δγ измерения углов 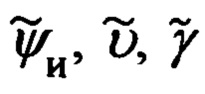 эволюции объекта (87)-(92), (116)-(119), а погрешности
эволюции объекта (87)-(92), (116)-(119), а погрешности 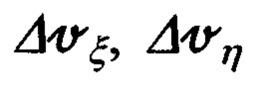 (68) формирования составляющих
(68) формирования составляющих  абсолютной линейной скорости объекта в проекциях на оси ОТГП ИНС Oξηζ (67) - ошибками
абсолютной линейной скорости объекта в проекциях на оси ОТГП ИНС Oξηζ (67) - ошибками 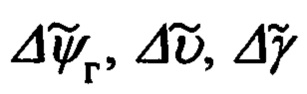 измерения углов гироскопического курса
измерения углов гироскопического курса 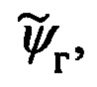 тангажа
тангажа 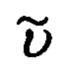 и крена
и крена 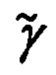 (74)-(79).
(74)-(79).
6. Итоговые погрешности Δn, Δе формирования идеальных значений географических координат ϕ, λ (109) текущего местоположения объекта с учетом погрешностей ΔRN, ΔRE, 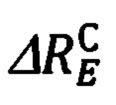 (99), (101) расчета главных радиусов кривизны земного эллипсоида вращения, определяют, также, как и погрешности
(99), (101) расчета главных радиусов кривизны земного эллипсоида вращения, определяют, также, как и погрешности 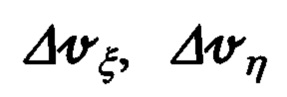 (79) формирования горизонтальных составляющих абсолютной линейной скорости объекта (67), (71), в функции параметров состояния ИНС таких, как αx, αy, αz, Δϕ, Δλ (79), (123).
(79) формирования горизонтальных составляющих абсолютной линейной скорости объекта (67), (71), в функции параметров состояния ИНС таких, как αx, αy, αz, Δϕ, Δλ (79), (123).
Для этого используют характерные для навигационных Δϕ, Δλ, Δχ и пилотажных 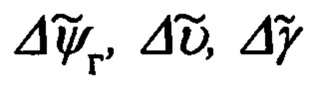 параметров ИНС кинематические соотношения их связи с малыми углами αx, αу, αz ухода ее реальной гироплатформы (60)-(61).
параметров ИНС кинематические соотношения их связи с малыми углами αx, αу, αz ухода ее реальной гироплатформы (60)-(61).
7. Для корректного математического описания позиционных и скоростных сигналов измерения оптимального фильтра-идентификатора ошибок ИНС формируют соответствующие уравнения связи (72), (112).
Левые части указанных уравнений принимают за соответствующие сигналы измерения (73), (113), а по их правым частям определяют соответствующие элементы матрицы наблюдения (82), (83), (125), (126), которые представляют в функции параметров состояния ИНС (81), для чего используют кинематические соотношения связи ошибок счисления основной тройки Δϕ, Δλ, Δχ навигационных параметров и углов 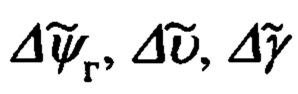 эволюции объекта с малыми углами αx, αу, αz ухода реальной ГП ИНС.
эволюции объекта с малыми углами αx, αу, αz ухода реальной ГП ИНС.
8. Процедуру оптимальной фильтрации и идентификации позиционных и скоростных сигналов измерения реализуют в соответствии с дискретным вариантом ее реализации, представленным векторно-матричными уравнениями/выражениями вида (52)-(58). При этом используют традиционную для ИНС модель ошибок, представленную системой дифференциальных уравнений 10-го порядка, которую расширяют за счет включения в нее системы из трех взаимосвязанных дифференциальных уравнений первого порядка (80), описывающих характер изменения координат Δξ, Δη, Δζ местоположения (размещения на объекте) ИНС относительно ОПС в проекциях на оси ОТГП ИНС Oξηζ.
9. По истечении времени оптимального оценивания, определяемого временем нахождения ОК в зоне оптического контакта с объектом и составляющего 5,5-6 минут, фильтр-идентификатор ошибок инерциальной информации останавливают, его входные сигналы и коэффициенты усиления обнуляют, а сам фильтр переводят в режим долгосрочного прогноза его оценок, используя для этого рекуррентную процедуру формирования ее априорных оценок (55).
Полученные в результате прогноза значения оценок используют для коррекции счисленных географических координат 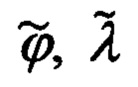 текущего местоположения объекта, горизонтальных составляющих Vx, Vy его абсолютной линейной скорости, угла
текущего местоположения объекта, горизонтальных составляющих Vx, Vy его абсолютной линейной скорости, угла 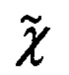 азимутальной ориентации ее гироплатформы, углов
азимутальной ориентации ее гироплатформы, углов 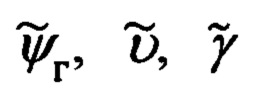 текущей ориентации объекта и его истинного курса
текущей ориентации объекта и его истинного курса 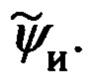 При этом коррекцию углов
При этом коррекцию углов 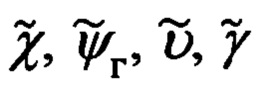 и
и 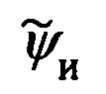 осуществляют после предварительного формирования оценок ошибок счисления/измерения углов
осуществляют после предварительного формирования оценок ошибок счисления/измерения углов 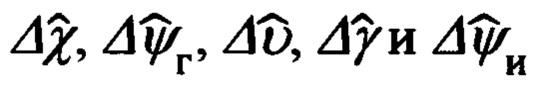 в соответствии с кинематическими соотношениями их связи с оценками малых углов
в соответствии с кинематическими соотношениями их связи с оценками малых углов 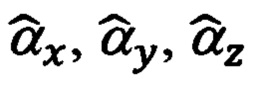 ухода реальной ГП ИНС (60), (61). Использование указанных соотношений позволяет достаточно просто реализовать коррекцию практически всех счисляемых и измеряемых инерциальной системой сигналов, которую осуществляют в «разомкнутом контуре». Описанная выше процедура коррекции навигационных и пилотажных параметров приведена в описании изобретения и представлена выражениями (148)-(163). При этом маневр, который предполагается использовать в рассматриваемом режиме коррекции, типа круговой циркуляции вокруг ОК (фиг. 7), следует рассматривать, как методический прием, обеспечивающий оценивание всех параметров состояния ИНС, включая и слабонаблюдаемые, такие, как азимутальный уход ГП αz и некомпенсированный дрейф εz курсового гироскопа.
ухода реальной ГП ИНС (60), (61). Использование указанных соотношений позволяет достаточно просто реализовать коррекцию практически всех счисляемых и измеряемых инерциальной системой сигналов, которую осуществляют в «разомкнутом контуре». Описанная выше процедура коррекции навигационных и пилотажных параметров приведена в описании изобретения и представлена выражениями (148)-(163). При этом маневр, который предполагается использовать в рассматриваемом режиме коррекции, типа круговой циркуляции вокруг ОК (фиг. 7), следует рассматривать, как методический прием, обеспечивающий оценивание всех параметров состояния ИНС, включая и слабонаблюдаемые, такие, как азимутальный уход ГП αz и некомпенсированный дрейф εz курсового гироскопа.
Из приведенного описания унифицированного способа оптимального оценивания ошибок инерциальной информации и ее коррекции по неподвижному наземному ориентиру с известными географическими координатами следует, что суть предлагаемого решения раскрыта и технический результат достигнут.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЗАЩИЩЕННЫЙ СПОСОБ ОПТИМАЛЬНОЙ ПРИВЯЗКИ К ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ | 2019 |
|
RU2713584C1 |
| СПОСОБ ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ ИНФОРМАЦИИ И ЕЁ КОРРЕКЦИИ ПО ИЗМЕРЕНИЯМ ДОПЛЕРОВСКОГО ИЗМЕРИТЕЛЯ СКОРОСТИ | 2015 |
|
RU2614192C1 |
| СПОСОБ ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ ИНФОРМАЦИИ И ЕЁ КОРРЕКЦИИ ПО ИЗМЕРЕНИЯМ СПУТНИКОВОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2015 |
|
RU2617565C1 |
| СПОСОБ ФОРМИРОВАНИЯ БАРОИНЕРЦИАЛЬНОЙ ВЫСОТЫ И ВЕРТИКАЛЬНОЙ СКОРОСТИ | 2019 |
|
RU2713583C1 |
| СПОСОБ ФОРМИРОВАНИЯ ВОЗДУШНО-СКОРОСТНЫХ ПАРАМЕТРОВ МАНЕВРЕННОГО ОБЪЕКТА | 2019 |
|
RU2713585C1 |
| СПОСОБ ОПТИМАЛЬНОЙ ПРИВЯЗКИ К ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ И ПРОГНОЗА ЕЁ ПАРАМЕТРОВ НА ОСНОВЕ МОДИФИЦИРОВАННОЙ, ИНВАРИАНТНОЙ К РЕЛЬЕФУ ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ УГЛОМЕСТНОЙ ПРОЦЕДУРЫ РАСЧЁТА ДАЛЬНОСТИ | 2016 |
|
RU2617373C1 |
| СПОСОБ ОПТИМАЛЬНОЙ ПРИВЯЗКИ К ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ И ПРОГНОЗА ЕЁ ПАРАМЕТРОВ НА ОСНОВЕ СУБОПТИМАЛЬНОЙ ПРОЦЕДУРЫ УГЛОВОГО СОПРОВОЖДЕНИЯ | 2016 |
|
RU2621374C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО ПРИЦЕЛИВАНИЯ ПО ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ | 2016 |
|
RU2629130C1 |
| СПОСОБ КОРРЕКЦИИ КОМПЛЕКСНОЙ ИНС ПО АНОМАЛИИ ГРАВИТАЦИОННОГО ПОЛЯ ЗЕМЛИ | 1985 |
|
SU1840368A1 |
| СПОСОБ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ | 2022 |
|
RU2806707C1 |
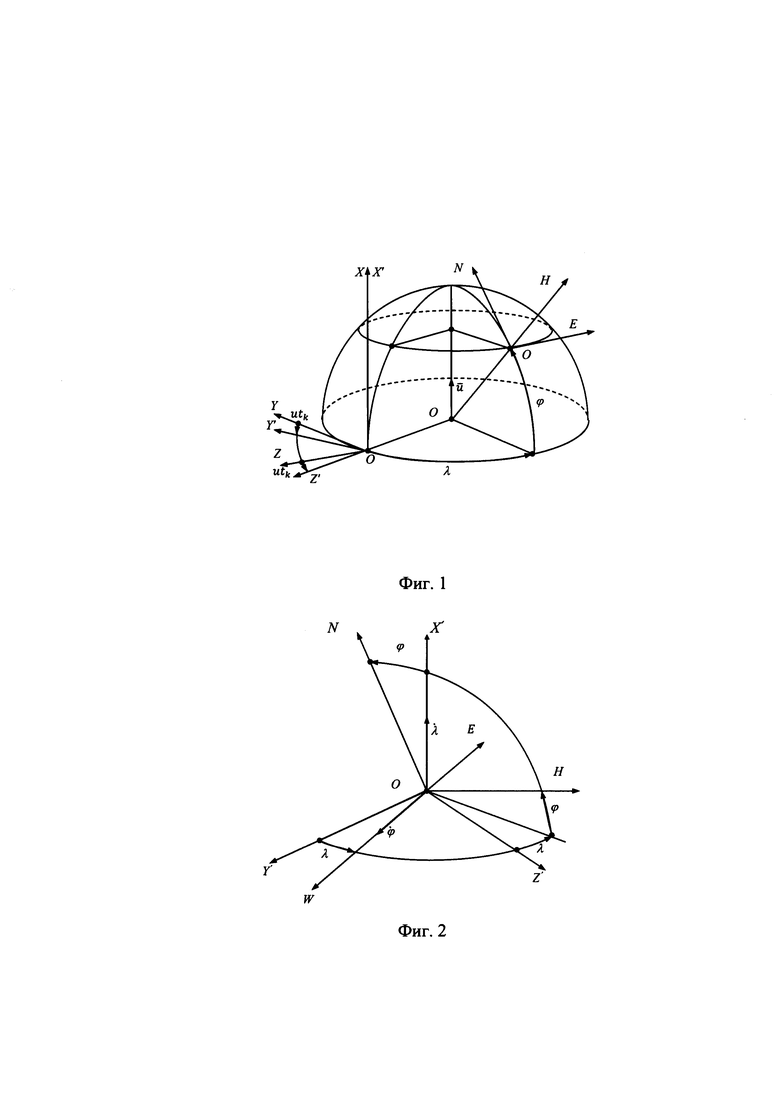
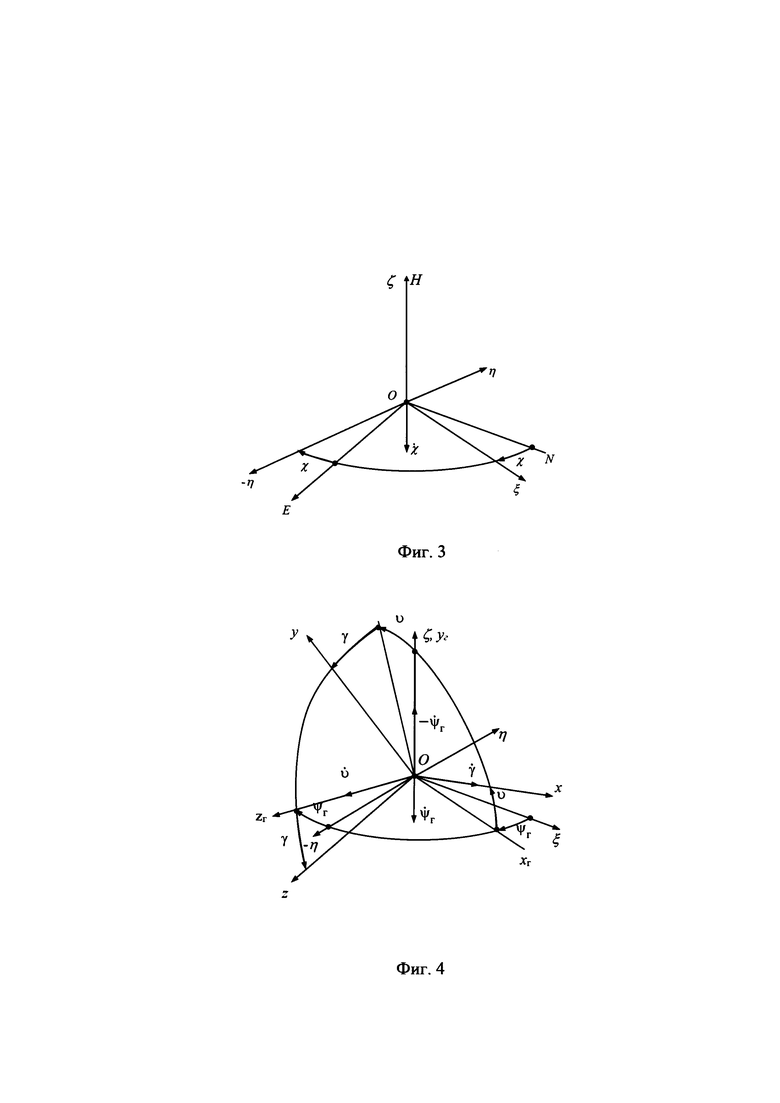
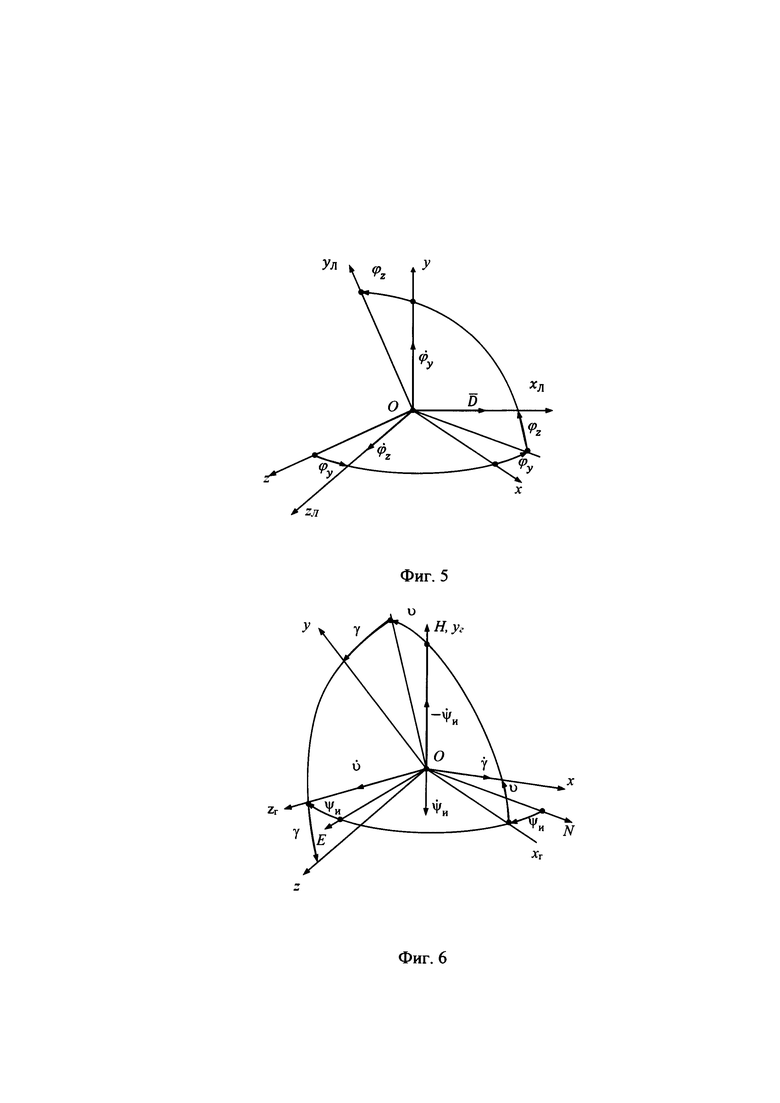
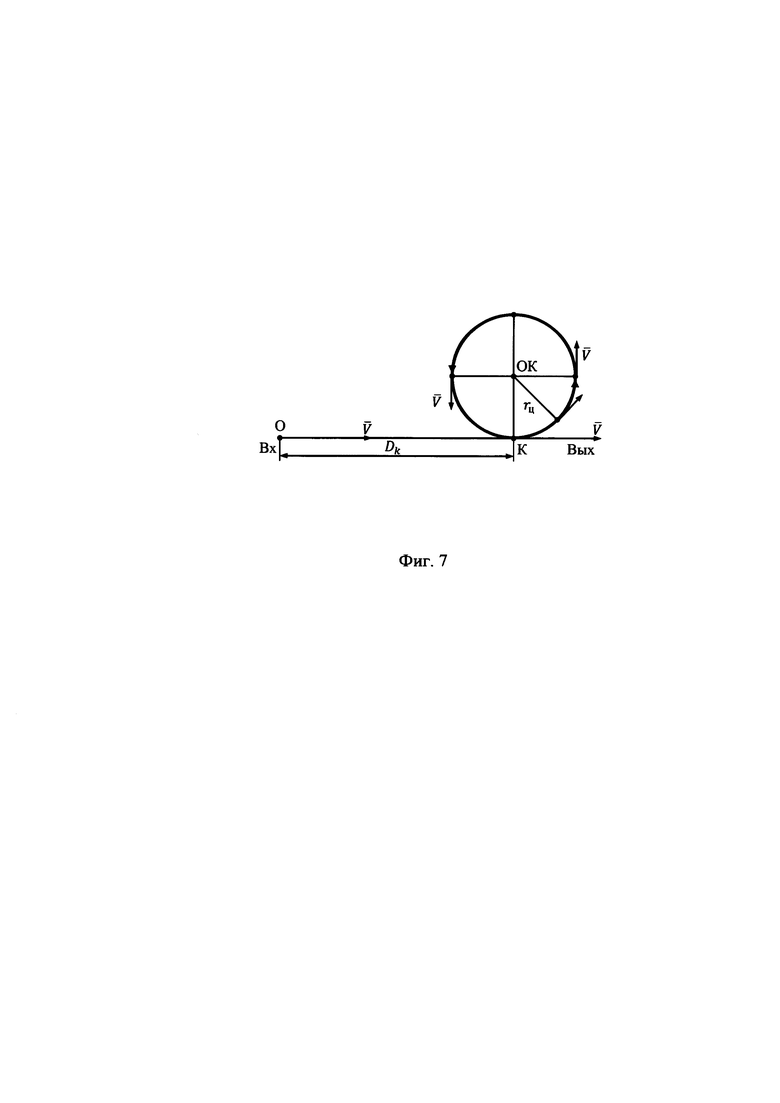
Изобретение относится к области измерительных информационных систем и комплексов боевых самолетов и вертолетов, в котором проводится разработка способа оптимального оценивания полного перечня параметров состояния инерциальной навигационной системы (ИНС) и эффективной коррекции измеряемой ей навигационной и пилотажной информации. Способ оптимального оценивания ошибок инерциальной навигационной системы и ее коррекции по неподвижному наземному ориентиру с известными географическими координатами включает угловое сопровождение неподвижного наземного ориентира коррекции (ОК) и дискретное измерение наклонной дальности до него в щадящем для лазерного дальномера из состава обзорно-прицельной системы режиме его работы с частотой излучающих посылок 0,5-1,0 Гц и основан на совместной обработке измеряемых при этом текущих углов визирования ОК и наклонной дальности до него, текущих углов истинного и гироскопического курсов, крена и тангажа объекта и счисленных ИНС географических координат его местоположения и текущей бароинерциальной высоты. При этом в режиме непрерывного углового сопровождения ОК одно-двухсекундные временные интервалы между соседними измерениями дальности до ОК заполняют ее десятигерцовыми расчетными значениями, которые формируют в соответствии с модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедурой определения наклонной дальности, предполагающей использование текущих бароинерциальной высоты объекта, косинуса угла между географической вертикалью и направлением на ОК, и сформированного по измерениям ОПС опорного значения высоты ОК над уровнем моря, при этом оценивание составляющих абсолютной линейной скорости объекта осуществляют в соответствии с кинематической моделью его движения относительно неподвижного наземного ОК в проекциях на оси инерциальной системы координат. При этом реализуются две параллельно работающие процедуры оптимального оценивания - основная и вспомогательная, первая из которых обеспечивает оценивание расширенного вектора параметров состояния ИНС и последующую коррекцию ее навигационных и пилотажных параметров, а вторая - формирование адекватных с СНС позиционных и скоростных сигналов, используемых в основной процедуре оптимального оценивания в качестве сигналов идеального измерителя. Технический результат изобретения – расширение функциональных возможностей прицельно-навигационного комплекса современного ЛА. 7 ил.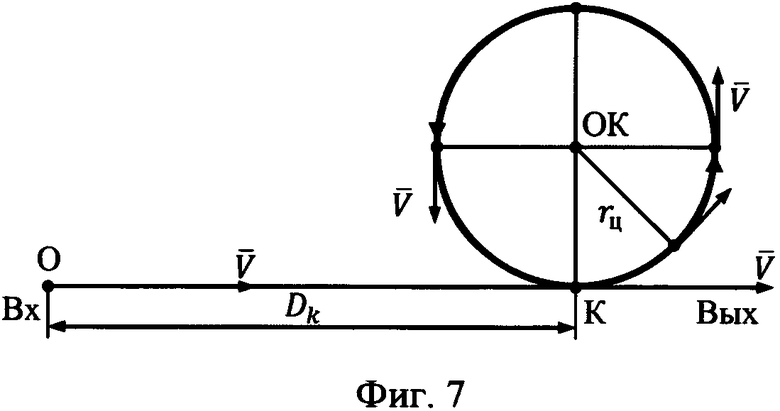
Способ оптимального оценивания ошибок инерциальной навигационной системы и ее коррекции по неподвижному наземному ориентиру с известными географическими координатами, включающий угловое сопровождение неподвижного наземного ориентира коррекции (ОК) и дискретное измерение наклонной дальности до него в щадящем для лазерного дальномера (ЛД) из состава обзорно-прицельной системы (ОПС) режиме его работы с частотой излучающих посылок 0,5-1,0 Гц и основанный на совместной обработке измеряемых при этом текущих углов ϕy, ϕz визирования ОК и наклонной дальности 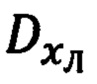 до него, текущих углов истинного
до него, текущих углов истинного 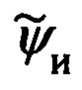 и гироскопического
и гироскопического 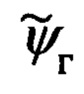 курсов, крена
курсов, крена 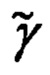 и тангажа
и тангажа 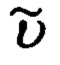 объекта и счисленных ИНС географических координат
объекта и счисленных ИНС географических координат 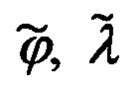 его местоположения и текущей бароинерциальной высоты
его местоположения и текущей бароинерциальной высоты 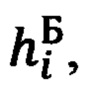 отличающийся тем, что в режиме непрерывного углового сопровождения ОК одно-двухсекундные временные интервалы между соседними измерениями дальности до ОК заполняют ее десятигерцовыми расчетными значениями, которые формируют в соответствии с модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедурой определения наклонной дальности, предполагающей использование текущих бароинерциальной высоты объекта, косинуса угла между географической вертикалью и направлением на ОК, и сформированного по измерениям ОПС опорного значения высоты ОК над уровнем моря, при этом оценивание составляющих абсолютной линейной скорости объекта осуществляют в соответствии с кинематической моделью его движения относительно неподвижного наземного ОК в проекциях на оси инерциальной системы координат (ИСК), чем обеспечивают кардинальное упрощение описывающих ее дифференциальных уравнений за счет естественной поканальной декомпозиции модели относительного движения объекта, которую, из соображений повышения точности оценивания, дополнительно, модифицируют, переходя от уравнений для составляющих абсолютной линейной скорости и ускорения объекта в полных сигналах к их вариациям относительно измеренных ИНС текущих значений, при этом компоненты абсолютной линейной скорости движения объекта относительно ОК используют как известное управление, а полученные в результате процедуры оптимальной фильтрации и идентификации оценки компонент дальности до ОК и составляющих абсолютной линейной скорости объекта используют для формирования позиционных и скоростных сигналов идеального измерителя, путем сравнения которых с соответствующими выходными сигналами ИНС формируют сигналы измерения оптимального фильтра-идентификатора ошибок ИНС и элементы его матрицы наблюдения, через которые осуществляют учет всех ошибок сигналов измерения, при этом процедуру их оптимальной фильтрации и идентификации реализуют в соответствии с традиционной для ИНС моделью ошибок, которую, из соображений корректности ее описания и точности оценивания, расширяют за счет включения в нее трех дифференциальных уравнений, описывающих характер изменения координат местоположения ИНС относительно ОПС в проекциях на оси опорного трехгранника гироплатформы (ОТГП) ИНС, по окончании оптимального оценивания ошибок ИНС, определяемого временем нахождения ОК в зоне оптического контакта с объектом, фильтр-идентификатор ошибок ИНС останавливают, его входные сигналы и коэффициенты усиления обнуляют, а сам фильтр переводят в режим долгосрочного прогноза полученных оценок, который реализуют в соответствии с рекуррентной процедурой формирования априорных ошибок ИНС, а полученные в результате прогноза значения ошибок ИНС используют для коррекции координат текущего местоположения объекта, горизонтальных составляющих его абсолютной линейной скорости, угла азимутальной ориентации ГП ИНС и углов текущей ориентации объекта.
отличающийся тем, что в режиме непрерывного углового сопровождения ОК одно-двухсекундные временные интервалы между соседними измерениями дальности до ОК заполняют ее десятигерцовыми расчетными значениями, которые формируют в соответствии с модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедурой определения наклонной дальности, предполагающей использование текущих бароинерциальной высоты объекта, косинуса угла между географической вертикалью и направлением на ОК, и сформированного по измерениям ОПС опорного значения высоты ОК над уровнем моря, при этом оценивание составляющих абсолютной линейной скорости объекта осуществляют в соответствии с кинематической моделью его движения относительно неподвижного наземного ОК в проекциях на оси инерциальной системы координат (ИСК), чем обеспечивают кардинальное упрощение описывающих ее дифференциальных уравнений за счет естественной поканальной декомпозиции модели относительного движения объекта, которую, из соображений повышения точности оценивания, дополнительно, модифицируют, переходя от уравнений для составляющих абсолютной линейной скорости и ускорения объекта в полных сигналах к их вариациям относительно измеренных ИНС текущих значений, при этом компоненты абсолютной линейной скорости движения объекта относительно ОК используют как известное управление, а полученные в результате процедуры оптимальной фильтрации и идентификации оценки компонент дальности до ОК и составляющих абсолютной линейной скорости объекта используют для формирования позиционных и скоростных сигналов идеального измерителя, путем сравнения которых с соответствующими выходными сигналами ИНС формируют сигналы измерения оптимального фильтра-идентификатора ошибок ИНС и элементы его матрицы наблюдения, через которые осуществляют учет всех ошибок сигналов измерения, при этом процедуру их оптимальной фильтрации и идентификации реализуют в соответствии с традиционной для ИНС моделью ошибок, которую, из соображений корректности ее описания и точности оценивания, расширяют за счет включения в нее трех дифференциальных уравнений, описывающих характер изменения координат местоположения ИНС относительно ОПС в проекциях на оси опорного трехгранника гироплатформы (ОТГП) ИНС, по окончании оптимального оценивания ошибок ИНС, определяемого временем нахождения ОК в зоне оптического контакта с объектом, фильтр-идентификатор ошибок ИНС останавливают, его входные сигналы и коэффициенты усиления обнуляют, а сам фильтр переводят в режим долгосрочного прогноза полученных оценок, который реализуют в соответствии с рекуррентной процедурой формирования априорных ошибок ИНС, а полученные в результате прогноза значения ошибок ИНС используют для коррекции координат текущего местоположения объекта, горизонтальных составляющих его абсолютной линейной скорости, угла азимутальной ориентации ГП ИНС и углов текущей ориентации объекта.
| СПОСОБ ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ ИНФОРМАЦИИ И ЕЁ КОРРЕКЦИИ ПО ИЗМЕРЕНИЯМ ДОПЛЕРОВСКОГО ИЗМЕРИТЕЛЯ СКОРОСТИ | 2015 |
|
RU2614192C1 |
| СПОСОБ ОПТИМАЛЬНОЙ ПРИВЯЗКИ К ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ И ПРОГНОЗА ЕЁ ПАРАМЕТРОВ НА ОСНОВЕ СУБОПТИМАЛЬНОЙ ПРОЦЕДУРЫ УГЛОВОГО СОПРОВОЖДЕНИЯ | 2016 |
|
RU2621374C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНЫХ УХОДОВ НАВИГАЦИОННЫХ СИСТЕМ ПОДВИЖНЫХ НОСИТЕЛЕЙ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2012 |
|
RU2504733C1 |
| Устройство для электрообработки жидкости | 1989 |
|
SU1724592A1 |
Авторы
Даты
2020-02-05—Публикация
2019-01-29—Подача