Способ определения истинного курса подвижного объекта относится к способам автономной навигации объектов с использованием нескольких датчиков без применения внешних источников информации, в частности глобальных навигационных спутниковых систем, а также без использования магнитного поля Земли (МПЗ) с соответствующими датчиками.
Известен способ определения истинного курса с помощью двухканального гироскопического датчика угловой скорости [1], заключающийся в предварительном согласовании измерительных осей датчика со связанными осями объекта, определении его углов тангажа, крена и широты местоположения и компенсации на их основе влияния проекций на измерительные оси вертикальной составляющей угловой скорости вращения Земли. Способ применим в условиях неподвижного наклонного объекта.
Недостатком способа [1] является низкая точность применительно к подвижному объекту, поскольку в нем не предусмотрен учет параметров линейного и углового движения последнего. К низкой точности также приводит исключение (компенсация) влияния вертикальной составляющей угловой скорости вращения Земли, рассматриваемой как мешающий фактор. При ненулевых углах тангажа и крена проекции этой составляющей при надлежащем использовании могут являться дополнительной к горизонтальной составляющей измерительной информацией. Кроме того, не определена процедура получения углов тангажа, крена и широты объекта. На практике при использовании только двухканального гироскопического датчика получение указанных углов невозможно.
Известны способы определения курса методом гирокомпасирования с применением гироскопического датчика угловой скорости для подвижного объекта [2, 3]. По своей сути эти способы являются распространением способа [1] на подвижный объект путем внесения в определяемый истинный курс соответствующих поправок на линейное [2] и угловое и линейное [3] движение объекта. При этом сохраняются недостатки способа [1], связанные с неучетом проекций вертикальной составляющей угловой скорости вращения Земли и неопределенностью процедуры получения углов тангажа, крена и широты объекта. Кроме того, в способах [2,3] дополнительно использованы значения путевой скорости, высоты, скоростей изменения углов рысканья, тангажа, крена, широты и долготы объекта, процедуры получения которых также не определены.
Наиболее близким к заявляемому способу является способ определения курса подвижного объекта [4], заключающийся в том, что на объекте устанавливают три акселерометра и трех датчика угловой скорости, так чтобы их оси и связанные оси объекта, определяющие углы его курса, тангажа и крена в выбранной системе координат, были параллельны, измеряют указанными акселерометрами и датчиками угловой скорости проекции векторов ускорения и угловой скорости объекта на соответствующие оси, по проекциям вектора ускорения, считая известным ускорение силы тяжести, определяют режим движения объекта по скорости: равномерный или ускоренный, при этом в равномерном режиме по данным акселерометров определяют углы тангажа и крена объекта, в ускоренном режиме по данным датчиков угловой скорости выбирают интервалы, в течение которых проекции вектора угловой скорости объекта могут считаться постоянными, на каждом интервале корректируют значения направляющих косинусов связанных осей объекта относительно осей выбранной системы координат.
Способ предполагает определение магнитного курса подвижного объекта, для чего проводятся измерения тремя магнитометрами проекций горизонтальной и вертикальной составляющих МПЗ с последующим вычислением по ним и углам тангажа и крена объекта, определяемым по показаниям акселерометров (при равномерном движении объекта) или датчиков угловой скорости (при ускоренном движении), магнитного курса подвижного объекта.
Недостатком способа [4] является его низкая точность. Это обусловлено следующими причинами.
Большинство задач высокоточной топогеодезической привязки, прецизионной навигации и наведения требует перехода от магнитного курса объекта к его истинному курсу (азимуту). Переход осуществляется введением в магнитный курс поправки на величину магнитного склонения. В ряде случаев (например, при задании дирекционных направлений в районе развертывания артиллерийских позиций) далее переходят к дирекционному углу. Делается это учетом сближения меридианов, величина которого стабильна и известна с высокой точностью.
Фактором, определяющим итоговую точность измерения углов (истинного курса, дирекционного), выступает точность знания магнитного склонения. Однако практически для всех указанных задач эта точность недостаточна для реализации требований, предъявляемых к их решениям. Главными причинами этого являются, во-первых, изменения во времени (вековые, годовые, суточные) и зависимость магнитного склонения от координат объекта, затрудняющие его высокоточный предварительный расчет, и, во-вторых, (что более существенно) искажения и возмущения (аномалии) МПЗ различного происхождения, исключающие возможность учета магнитного склонения без предварительной калибровки в условиях локального аномального поля. Последнее для оперативных задач привязки, навигации и наведения в реальном (близком к реальному) масштабе времени невозможно.
Техническим результатом использования заявляемого способа является повышение точности измерения истинного курса подвижного объекта.
Для получения указанного технического результата в способе определения курса подвижного объекта, заключающемся в том, что на объекте устанавливают три акселерометра и трех датчика угловой скорости, так чтобы их оси и связанные оси объекта, определяющие углы его курса, тангажа и крена в выбранной системе координат, были параллельны, измеряют указанными акселерометрами и датчиками угловой скорости проекции векторов ускорения и угловой скорости объекта на соответствующие оси, по проекциям вектора ускорения, считая известным ускорение силы тяжести, определяют режим движения объекта по скорости: равномерный или ускоренный, при этом в равномерном режиме по данным акселерометров определяют углы тангажа и крена объекта, в ускоренном режиме по данным датчиков угловой скорости выбирают интервалы, в течение которых проекции вектора угловой скорости объекта могут считаться постоянными, на каждом интервале корректируют значения направляющих косинусов связанных осей объекта относительно осей выбранной системы координат, по текущим значениям истинного курса объекта определяют его режим движения по курсу: прямолинейный или непрямолинейный, при прямолинейном равномерном движении истинный курс определяют по значениям углов тангажа и крена и данным датчиков угловой скорости о проекциях вектора угловой скорости вращения Земли, при непрямолинейном равномерном или ускоренном движении истинный курс определяют по корректируемым значениям направляющих косинусов продольной связанной оси объекта относительно направлений на географические север и восток и местной вертикали, при переходе объекта в режим непрямолинейного равномерного или ускоренного движения в качестве начального условия коррекции указанных направляющих косинусов используют их значения, вычисленные по углам истинного курса и тангажа на момент начала движения неподвижного объекта или окончания его равномерного прямолинейного движения.
Принципиальным отличием заявляемого способа от прототипа является отказ от магнитометрического способа определения курса подвижного объекта за счет использования иного, более точного метода - метода бесплатформенной инерциальной навигации. Этот метод, в отличие от прототипа, позволяет определить истинный курс подвижного объекта с использованием трех акселерометров и трех датчиков угловой скорости, исключив три магнитометра.
Заявляемый способ иллюстрируют следующие графические материалы.
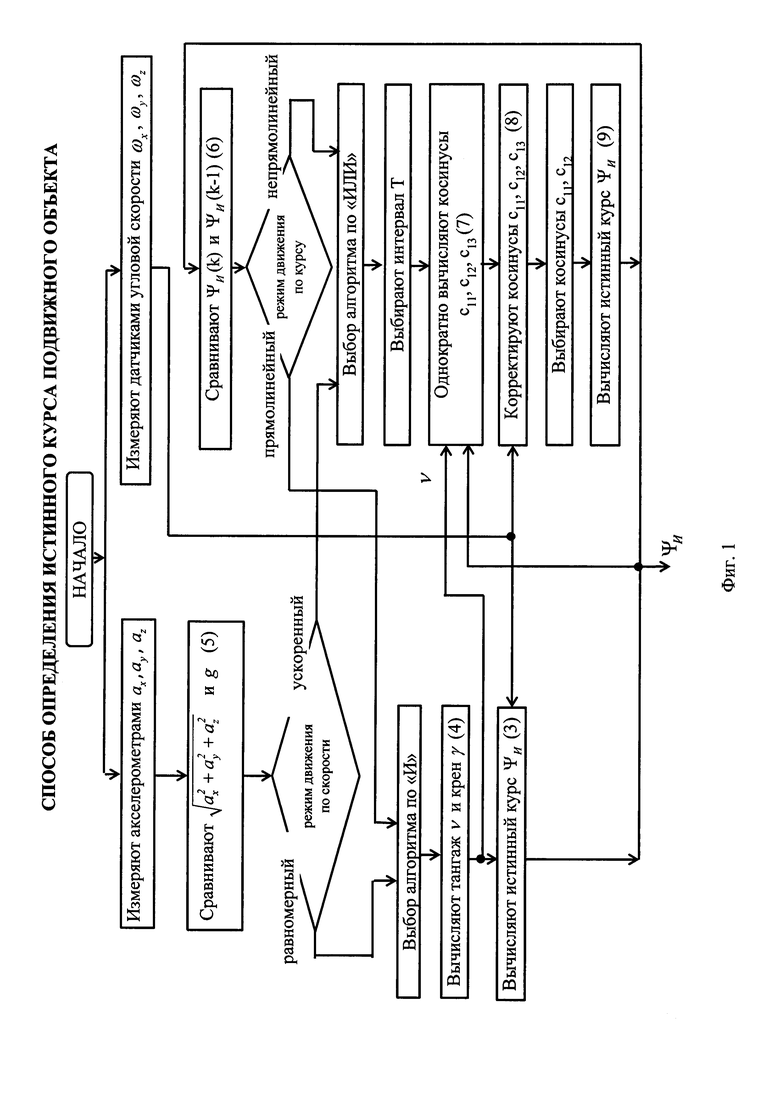
Фиг. 1 - Алгоритм работы заявляемого способа, где в операторах алгоритма в круглых скобках указаны номера формул, приведенных ниже.
Существенными отличиями заявляемого способа по сравнению с прототипом являются.
1. По текущим значениям истинного курса объекта определяют режим движения по курсу: прямолинейный или непрямолинейный. Совместно с данными акселерометров, фиксирующих режим движения по скорости: равномерный или ускоренный, это позволяет определять прямолинейный равномерный режим движения объекта (частным случаем режима является неподвижный объект). В этом режиме по углам тангажа и крена, рассчитываемым непосредственно по данным акселерометров, и измеряемым ДУС проекциям угловой скорости вращения Земли аналитически вычисляется истинный курс объекта. Этим обеспечивается высокая точность определения курса, поскольку угловая скорость вращения Земли является прецизионной фундаментальной константой, не подверженной никаким значимым искажениям и возмущениям.
В прототипе режимы движения объекта по курсу не рассматриваются, а в режиме равномерного движения курс вычисляется по проекциям МПЗ, зависимого от времени и координат объекта и, что более существенно, от искажений и возмущений различного происхождения. Это приводит к низкой точности определения курса. Кроме того, углы тангажа и крена вычисляются не непосредственно по данным акселерометров, а более сложно через предварительно рассчитываемые направляющие косинусы связанных осей объекта относительно местной вертикали.
2. При непрямолинейном и(или) ускоренном движении истинный курс определяют по корректируемым данными ДУС значениям трех направляющих косинусов продольной связанной оси объекта относительно направлений на географические север и восток и местной вертикали без привлечения углов тангажа и крена. При использовании прецизионных ДУС этим обеспечивается высокая точность определения текущего истинного курса подвижного объекта.
В прототипе при ускоренном движении курс, как и прежде, вычисляется с использованием проекций МПЗ со всеми его недостатками, а для расчета необходимых углов тангажа и крена требуется сложная вычислительная процедура пошаговой коррекции всех девяти элементов матрицы направляющих косинусов связанных осей объекта относительно осей магнитной географической системы координат.
3. При переходе объекта в режим непрямолинейного и(или) ускоренного движения в качестве начального условия коррекции трех указанных направляющих косинусов используют их значения, вычисленные по углам истинного курса и тангажа на момент начала движения неподвижного объекта или окончания его прямолинейного равномерного движения. Высокая точность исходного (начального) истинного курса, полученного на основе проекций угловой скорости вращения Земли (см. п. 1), гарантирует высокую точность последующего курсового определения по данным ДУС, рассмотренного в п. 2.
В прототипе в качестве начального условия коррекции используют значения полной матрицы направляющих косинусов, вычисленное по углам магнитного курса, тангажа и крена на момент окончания равномерного движения объекта. Такая вычислительная процедура является более трудоемкой, и, главное, как и в предыдущих случаях наследует все недостатки используемого МПЗ.
Заявляемый способ можно пояснить следующим образом, см. Фиг. 1.
Используются две системы координат.
а) Географическая система координат (СК) ON, ОЕ, Oh с началом в центре масс подвижного объекта. Оси ON, ОЕ лежат в плоскости местного горизонта, ось ON направлена на географический север (полюс), ось ОЕ - на географический восток. Ось Oh совпадает с местной вертикалью и направлена вверх.
Данная система координат непосредственно связана с векторами угловой скорости вращения Земли Ω и ускорения силы тяжести g. А именно, северная ось ON совпадает по направлению с горизонтальной составляющей Ωг=Ωcosϕ угловой скорости Ω (здесь ϕ - широта места объекта), ось Oh - с ее вертикальной составляющей Ωв=Ωsinϕ. Проекция угловой скорости Ω на восточную ось ОЕ равна нулю. Аналогично, вертикальная проекция вектора ускорения g равна его модулю g, две горизонтальные проекции равны нулю.
б) Связанная СК OXYZ с тем же началом. Оси OX, OY совпадают с продольной и поперечной строительными осями объекта. Ось OZ перпендикулярна этим осям (вертикальная ось). При нулевых углах тангажа ν и крена γ объекта оси OX, OY лежат в плоскости местного горизонта, ось OZ перпендикулярна этой плоскости и направлена вверх. Ось ОХ совпадает с направлением движения объекта. Ориентация оси ОХ относительно оси ON определяет истинный курс подвижного объекта ΨИ.
Оси чувствительности соосных акселерометров и датчиков угловой скорости совпадают с осями СК OXYZ.
При произвольных углах ΨИ, ν, γ взаимная ориентация систем координат определяется матрицей направляющих косинусов вида:
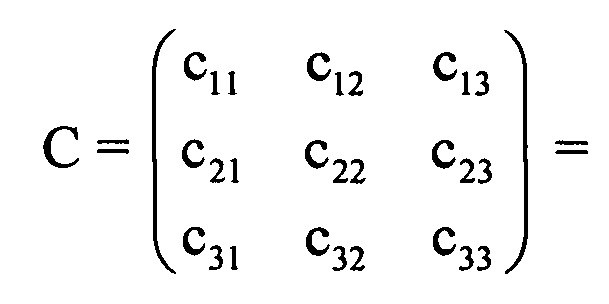
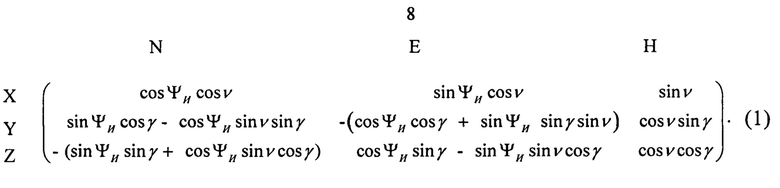
Из (1) видно, что составляющие угловой скорости вращения Земли Ωг, Ωв связаны с измерениями их проекций ωхз, ωуз, ωzз на оси чувствительности ДУС соотношениями:
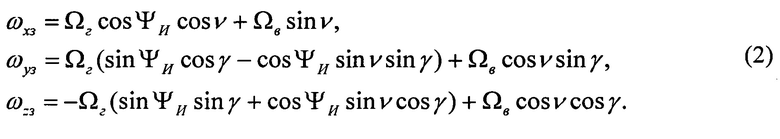
Если курс объекта неизменен (объект неподвижен или движется прямолинейно), а углы тангажа ν и крена γ известны и постоянны, то, разрешая систему уравнений (2) относительно неизвестного истинного курса ΨИ, приходим к выражению:
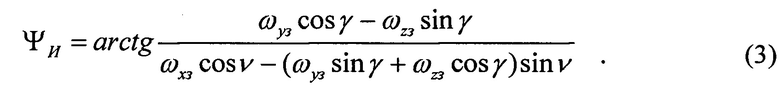
В частном случае при ν = γ = 0 справедливо известное равенство [5]:
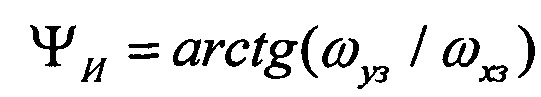
При равномерном прямолинейном движении объекта (заметим, что неподвижный объект есть частный случай равномерного движения с нулевой линейной скоростью) углы ν, γ определяются без предварительного расчета направляющих косинусов с13, с23, c33, как это делается в прототипе, а непосредственно по показаниям акселерометров ах, ау, аz:
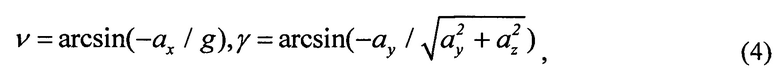
где ускорение силы тяжести g считается известным и направлено вертикально вниз, т.е. со знаком "минус".
Определение режима движения объекта (равномерный или ускоренный) проводится, как и в прототипе, проверкой выполнения равенства:

с допуском Δg, зависящим от точности используемых акселерометров.
Правилом определения прямолинейного (непрямолинейного) движения служит проверка выполнения равенства:

с допуском ΔΨ, зависящим от точности используемых ДУС. Здесь ΨИ(k), ΨИ(k-1) - текущие значения истинного курса объекта в соседние моменты времени tk, tk-1.
Таким образом, в режиме прямолинейного равномерного движения объекта (Выбор алгоритма по «И», Фиг. 1) измерение истинного курса ΨИ проводится по данным ДУС ωхз, ωуз, ωzз и акселерометров ах, ау, az в соответствии с соотношениями (3), (4). По сути, данный режим является режимом начальной выставки бесплатформенной инерциальной навигационной системы (БИНС), а измеренный курс ΨИ есть не что иное, как гирокомпасный азимут.
Реализация данного режима требует определенного времени (длительности участка равномерного прямолинейного движения объекта). Применение современных высокочувствительных ДУС (гироскопов) обеспечивает достаточно малое время выставки. Так, при использовании миниатюрных волновых твердотельных гироскопов с самокалибровкой [5] приемлемая точность достигается за 8-60 с, что вполне допустимо для задач топогеодезии, навигации и наведения.
Рассмотрим непрямолинейный и(или) ускоренный режимы (Выбор алгоритма по «ИЛИ», Фиг. 1)
При непрямолинейном движении объекта, когда равенство (6) нарушается, соотношение (3) становится несправедливым. Это обусловлено тем, что при непрямолинейном движении в измеряемых ДУС величинах ωх, ωу, ωz, помимо проекций ωxз, ωуз, ωzз, присутствуют (складываются) проекции ωx0, ωу0, ωz0 угловой скорости собственного вращения объекта.
Для реальных подвижных объектов обычно их значения значительно превышают значения ωхз, ωуз, ωzз, что позволяет в этом случае при вычислениях считать ωх=ωх0, ωу=ωу0, ωz=ωz0.
При ускоренном движении равенство (5) нарушается присутствием в показаниях акселерометров ах, ау, az дополнительных составляющих, вызванных собственным неизвестным линейным ускорением объекта. Как следствие, становятся несправедливыми соотношения (4).
В результате при непрямолинейном и(или) ускоренном движении объекта переходят к процедуре пошаговой коррекции направляющих косинусов.
Для этого, используя данные о возможной динамике объекта и(или) данные ДУС, выбирают интервал Т, в течение которого угловая скорость объекта может считаться постоянной.
Процедура пошаговой коррекции направляющих косинусов состоит в вычислении элементов матрицы (1):
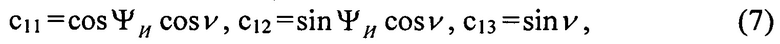
определяющих пространственное положение продольной связанной оси объекта ОХ относительно направлений на географические север и восток и местной вертикали. Процедура проводится по рекуррентному алгоритму: 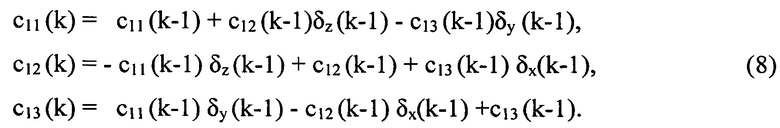
Здесь δx=ωхТ, δу=ωуТ, δz=ωzT - парциальные (пошаговые) приращения углов, Т=tk - tk-1 - интервалы времени (шаги), в течение которых проекции ωх, ωу, ωz могут считаться постоянными, k - номер очередного интервала (шага).
Последовательно выполняя алгоритм (8), получают пошаговые значения направляющих косинусов с11(k), C12(k), по которым вычисляют текущее (пошаговое) значение истинного курса подвижного объекта:

При этом начальные значения косинусов с11(0), c12(0), с13(0) соотношений (7) вычисляют по углам истинного курса ΨИ(0) и тангажа ν(0) на момент начала движения неподвижного объекта или окончания его прямолинейного равномерного движения. При возвращении к режиму прямолинейного равномерного движения (равенства (5), (6) восстанавливаются) также возвращается прежний порядок вычислений по формулам (3), (4) и так далее.
Отметим, что реализация соотношений (8), (9) по своей сущности является вариантом использования ДУС в гироазимутальном режиме (режиме гироскопа направления) работы БИНС.
Важно подчеркнуть, что в отличие от прототипа, где приходится корректировать все девять элементов матрицы направляющих косинусов (соотношения (8) описания прототипа), в заявляемом способе достаточно коррекции трех направляющих косинусов (соотношения (8) данного описания).
Рассмотрим возможность технической реализации заявляемого способа определения истинного курса подвижного объекта.
Для мобильного исполнения БИНС трехосевые акселерометры и датчики угловой скорости, соответствующие заявляемому способу, могут быть реализованы в виде малогабаритных микроэлектромеханических систем, содержащихся, например, в большинстве обычных смартфонов. В качестве более современной и точной технологии изготовления может быть использован миниатюрный волновой твердотельный гироскоп [5]. Среди множества вариантов исполнения акселерометров и ДУС следует выбирать образцы, удовлетворяющие по точности измерений.
Современные навигационные системы реализуются по единой схеме: совокупность измерителей - трехосных акселерометров и датчиков угловой скорости - через соответствующие преобразователи и интерфейсы подключается к компьютеру, который обычно (из-за необходимости вычисления прямых и обратных тригонометрических функций) реализуется в виде цифрового процессора обработки сигналов. Результаты обработки входной информации - тангаж ν, крен γ и истинный курс ΨИ - поступают потребителю. Естественно, что все такие системы работают в дискретном времени, что согласуется с пошаговым способом коррекции направляющих косинусов продольной связанной оси объекта относительно направлений на географические север и восток и местной вертикали в режимах непрямолинейного равномерного или ускоренного движения объекта.
Таким образом, заявляемый способ определения истинного курса подвижного объекта может быть реализован и обеспечивает повышение его точности.
Источники информации
1. Патент RU 2176780. «Способ определения истинного курса с помощью двухканального гироскопического датчика угловой скорости». - Опубликовано: 10.12.2001. Бюл. №34.
2. Патент RU 2210741. «Способ гирокомпасирования с применением гироскопического датчика угловой скорости при линейном движении объекта». - Опубликовано: 20.08.2003. Бюл. №23.
3. Патент RU 2210742. «Способ гирокомпасирования с применением гироскопического датчика угловой скорости при угловом и линейном движении объекта». - Опубликовано: 20.08.2003. Бюл. №23.
4. Патент RU 2629539. «Способ измерения магнитного курса подвижного объекта». - Опубликовано: 29.08.2017. Бюл. №25.
5. Мейер Д., Розелле Д. Инерциальная навигационная система на основе миниатюрного волнового твердотельного гироскопа// Гироскопия и навигация. 2012. №3(78). С. 45-54.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СЧИСЛЕНИЯ КООРДИНАТ ПРИ НЕОРТОГОНАЛЬНОЙ ОРИЕНТАЦИИ ВХОДНЫХ ОСЕЙ ИЗМЕРИТЕЛЕЙ ПАРАМЕТРОВ УГЛОВОГО ДВИЖЕНИЯ | 2020 |
|
RU2785971C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ НАЗЕМНОГО ПОДВИЖНОГО ОБЪЕКТА | 2018 |
|
RU2697859C1 |
| СПОСОБ ИЗМЕРЕНИЯ МАГНИТНОГО КУРСА ПОДВИЖНОГО ОБЪЕКТА | 2016 |
|
RU2629539C1 |
| Способ коррекции бесплатформенной инерциальной навигационной системы | 2016 |
|
RU2635820C1 |
| Способ измерения магнитного курса подвижного объекта | 2024 |
|
RU2831224C1 |
| Способ коррекции углов ориентации БИНС | 2022 |
|
RU2796328C1 |
| Способы формирования данных об ориентации объекта и навигационный комплекс летательного аппарата для их реализации | 2020 |
|
RU2745083C1 |
| Способ определения параметров ориентации объекта при помощи полуаналитической инерциальной навигационной системы с географической ориентацией осей четырехосной гироплатформы | 2022 |
|
RU2782334C1 |
| СПОСОБ ИЗМЕРЕНИЯ МАГНИТНОГО КУРСА ПОДВИЖНОГО ОБЪЕКТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2262075C1 |
| СПОСОБ ПОЛЕВОЙ КАЛИБРОВКИ МАГНИТНОГО КОМПАСА | 2018 |
|
RU2674535C1 |
Изобретение относится к способам автономной навигации объектов с использованием трехосевых акселерометров и датчиков угловой скорости (ДУС) без применения внешних источников информации, в частности глобальных навигационных спутниковых систем и магнитного поля Земли. Способ предполагает определение режимов движения объекта: равномерный или ускоренный, а также прямолинейный или непрямолинейный. В прямолинейном равномерном режиме истинный курс вычисляют по данным акселерометров, определяющих углы тангажа и крена, и ДУС, формирующих проекции вектора угловой скорости Земли. В остальных режимах выбирают интервалы, в течение которых проекции вектора угловой скорости объекта постоянны, на каждом интервале по данным ДУС корректируют направляющие косинусы продольной оси объекта, по значениям которых рассчитывают истинный курс. Данное изобретение позволяет повысить точность измерения истинного курса подвижного объекта. 1 ил.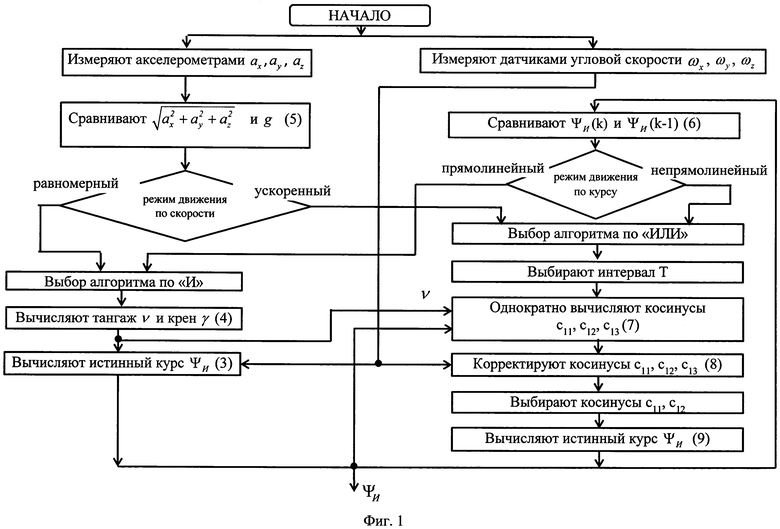
Способ определения истинного курса подвижного объекта, заключающийся в том, что на объекте устанавливают три акселерометра и три датчика угловой скорости, так чтобы их оси и связанные оси объекта, определяющие углы его курса, тангажа и крена в выбранной системе координат, были параллельны, измеряют указанными акселерометрами и датчиками угловой скорости проекции векторов ускорения и угловой скорости объекта на соответствующие оси, по проекциям вектора ускорения, считая известным ускорение силы тяжести, определяют режим движения объекта по скорости: равномерный или ускоренный, при этом в равномерном режиме по данным акселерометров определяют углы тангажа и крена объекта, в ускоренном режиме по данным датчиков угловой скорости выбирают интервалы, в течение которых проекции вектора угловой скорости объекта могут считаться постоянными, на каждом интервале корректируют значения направляющих косинусов связанных осей объекта относительно осей выбранной системы координат, отличающийся тем, что по текущим значениям истинного курса объекта определяют его режим движения по курсу: прямолинейный или непрямолинейный, при прямолинейном равномерном движении истинный курс определяют по значениям углов тангажа и крена и данным датчиков угловой скорости о проекциях вектора угловой скорости вращения Земли, при непрямолинейном равномерном или ускоренном движении истинный курс определяют по корректируемым значениям направляющих косинусов продольной связанной оси объекта относительно направлений на географические север и восток и местной вертикали, при переходе объекта в режим непрямолинейного равномерного или ускоренного движения в качестве начального условия коррекции указанных направляющих косинусов используют их значения, вычисленные по углам истинного курса и тангажа на момент начала движения неподвижного объекта или окончания его прямолинейного равномерного движения.
| СПОСОБ ИЗМЕРЕНИЯ МАГНИТНОГО КУРСА ПОДВИЖНОГО ОБЪЕКТА | 2016 |
|
RU2629539C1 |
| KR 1020110108208 A, 05.10.2011 | |||
| JP 2008045932 A, 28.02.2008 | |||
| СПОСОБ НАВИГАЦИИ ДВИЖУЩИХСЯ ОБЪЕКТОВ | 2014 |
|
RU2559820C1 |
| СИСТЕМА ОЦЕНИВАНИЯ ТОЧНОСТИ ПРОГНОЗИРОВАНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ (ИСЗ) | 2009 |
|
RU2397927C1 |
Авторы
Даты
2018-11-07—Публикация
2017-10-13—Подача