Предлагаемое изобретение относится к электроэнергетике и может быть использовано для определения места повреждения на воздушных линиях электропередачи, оборудованных грозозащитным тросом по всей длине.
Известен способ определения места повреждения при коротких замыканиях на землю воздушных линий электропередачи, оборудованных грозозащитным тросом [Авторское свидетельство №533886, МПК G01R 31/08, опубл. 30.10.76, бюлл. №40]. Согласно способу, измеряют и запоминают модули тока и напряжения нулевой последовательности на одном конце линии, дополнительно измеряют и запоминают на от же конце модуль тока нулевой последовательности в грозозащитном тросе поврежденной линии, а расстояние до места короткого замыкания на землю определяют по формуле:
l = (L⋅U0') / [(Zл0 - ZM)⋅I0' + (Zт0 - ZM)⋅Iт0'], (1)
где I0', U0' - соответственно модули тока и напряжения нулевой последовательности, измеряемые на подстанции, откуда ведется расчет l; Iт0' - модуль тока нулевой последовательности, измеряемый в грозозащитном тросе на той же подстанции; Zл0 - сопротивление нулевой последовательности линии электропередачи; Zт0 - сопротивление нулевой последовательности грозозащитного троса; ZM - сопротивление взаимоиндукции между линией электропередачи и грозозащитным тросом; L - длина линии электропередачи (троса).
Недостатками способа являются необходимость измерения модуля тока нулевой последовательности в грозозащитном тросе, а также низкая точность, связанная с некоторыми принятыми допущениями при получении расчетной формулы (1).
Известен способ определения поврежденного участка линии электропередачи с грозозащитным тросом [Авторское свидетельство №744381, МПК G01R 31/08, опубл. 30.06.80, бюлл. №24], основанный на измерении величины тока повреждения в деталях опоры и сравнении измеренной величины тока повреждения с допустимым значением этого тока. Измерение величины и направления токов повреждения производят на участках линии электропередачи с каждой стороны от опоры, сравнивают направления токов повреждения на участках линии электропередачи с каждой стороны от опоры с направлением тока повреждения в деталях опоры и выделяют участки линии электропередачи с токами повреждения, совпадающими по направлению с током повреждения в деталях опоры, при этом поврежденный участок определяют по выделенному участку линии электропередачи, а поврежденные опоры по наличию двух выделенных участков линии электропередачи.
Недостатком способа является сложность реализации, связанная с необходимостью проведения измерений на разных опорах и участках линии электропередачи, а также большие временные затраты на выполнение таких измерений.
Наиболее близким техническим решением является способ одностороннего определения места повреждения воздушной линии электропередачи [Аржанников, Е.А. Определение места короткого замыкания на высоковольтных линиях электропередачи / Е.А. Аржанников, В.Ю. Лукоянов, М.Ш. Мисриханов; под ред. В.А. Шуина. - М.: Энергоатомиздат, 2003, - 272 с. (стр. 47-55)], согласно которому производят определение поврежденной фазы линии электропередачи, измеряют фазные напряжения и токи аварийного и доаварийного режимов в начале линии электропередачи, определяют симметричные составляющие токов по измеренным фазным токам, определяют чисто аварийный ток прямой последовательности, как разность токов прямой последовательности аварийного и доаварийного режимов, в выражении для расчета расстояния до места повреждения используют опорный ток, в качестве которого выбирают ток нулевой, обратной последовательностей или чисто аварийный ток прямой последовательности, а расстояние до места повреждения рассчитывают по выражению:
LК = Im [ ф/
ф/ оп] / Im [Z1уд.Л⋅(
оп] / Im [Z1уд.Л⋅( ф + К⋅
ф + К⋅ 0) /
0) / оп], (2)
оп], (2)
где  ф,
ф,  ф - комплексные напряжения и ток поврежденной фазы;
ф - комплексные напряжения и ток поврежденной фазы;  оп - опорный ток;
оп - опорный ток;  0 - ток нулевой последовательности; Z1уд.Л - комплексное удельное сопротивление прямой последовательности линии электропередачи; К - комплексный коэффициент компенсации тока нулевой последовательности, К = (Z0уд.Л - Z1уд.Л) / Z1уд.Л; Z0уд.Л - комплексное удельное сопротивление нулевой последовательности линии электропередачи.
0 - ток нулевой последовательности; Z1уд.Л - комплексное удельное сопротивление прямой последовательности линии электропередачи; К - комплексный коэффициент компенсации тока нулевой последовательности, К = (Z0уд.Л - Z1уд.Л) / Z1уд.Л; Z0уд.Л - комплексное удельное сопротивление нулевой последовательности линии электропередачи.
Недостатком способа-прототипа является низкая точность определения расстояния до места повреждения на воздушных линиях электропередачи, оборудованных грозозащитным тросом.
К основным источникам ошибок способов определения места повреждения (ОМП) высоковольтных воздушных линий электропередачи (ЛЭП) по параметрам аварийного режима (ПАР), в том числе и способа-прототипа, следует отнести влияние: сопротивления повреждения воздушной ЛЭП, ее нагрузки, возможной подпитки с удаленного конца, взаимной индукции параллельных ЛЭП, апериодической составляющей тока, неточного задания параметров ЛЭП и других факторов.
В состав возможного сопротивления повреждения воздушной ЛЭП, как правило, включают три компоненты сопротивления: электрической дуги, заземления опоры, а также объектов, располагающихся на пути распространения аварийного тока [Аржанников, Е. А. Определение места короткого замыкания на высоковольтных линиях электропередачи / Е. А. Аржанников, В. Ю. Лукоянов, М. Ш. Мисриханов; под ред. В. А. Шуина. - М.: Энергоатомиздат, 2003. - 272 с]. Электрическая дуга обычно представляется активным сопротивлением, зависящим от тока дуги. Сопротивление заземления опор имеет преимущественно резистивный характер, и предполагается, что его значение не зависит от тока повреждения. В число возможных дополнительных объектов на пути распространения аварийного тока могут, например, входить сельскохозяйственная и другая техника, древесно-кустарниковая растительность, здания, другие предметы. Их сопротивление также считается резистивным, а его значение может варьироваться от нуля до очень больших значений, поэтому сопротивление короткого замыкания характеризуют как непредсказуемую величину.
Исходя из предположения резистивности сопротивления повреждения, разработано подавляющее большинство алгоритмов одностороннего ОМП ЛЭП по ПАР [Аржанников, Е. А. Определение места короткого замыкания на высоковольтных линиях электропередачи / Е. А. Аржанников, В. Ю. Лукоянов, М. Ш. Мисриханов; под ред. В. А. Шуина. - М.: Энергоатомиздат, 2003. - 272 с].
Однако в работе [Висящев А.Н., Пленков Э.Р., Федосов Д.С. Оценка величины и характера переходного сопротивления в месте короткого замыкания на воздушных линиях электропередачи высокого напряжения // Интеллектуальная Электротехника. 2023. № 2. С. 78-89. DOI: 10.46960/2658-6754_2023_2_78] показано влияние на величину и характер сопротивления повреждения способа заземления грозозащитного троса. Отмечено, что отсутствие учета реактивной составляющей переходного сопротивления при однофазных коротких замыканиях, в том числе из-за влияния грозотроса, приводит к появлению погрешностей до 10% и более при применении наиболее простых методов ОМП по замерам токов и напряжений с одной стороны ЛЭП.
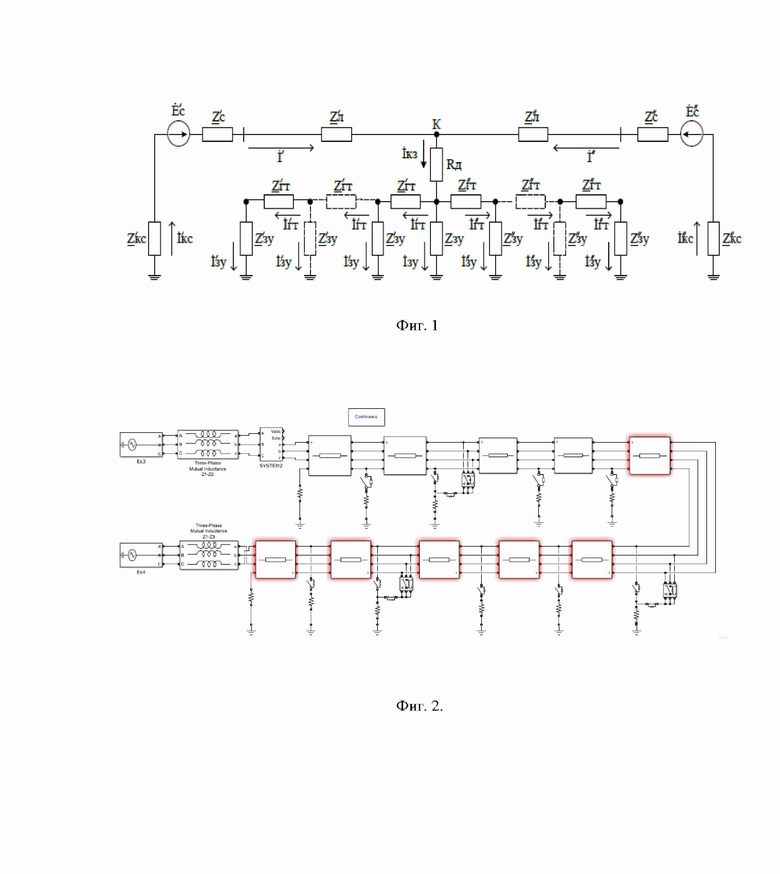
Оценку влияния величины и характера сопротивления повреждения на точность одностороннего ОМП ЛЭП по ПАР выполним с использованием модели одноцепной воздушной ЛЭП напряжением 110 кВ с грозозащитным тросом (ГТ), соответствующая эквивалентной схеме (фиг. 1) [Висящев А.Н., Пленков Э.Р., Федосов Д.С. Оценка величины и характера переходного сопротивления в месте короткого замыкания на воздушных линиях электропередачи высокого напряжения // Интеллектуальная Электротехника. 2023. № 2. С. 78-89. DOI: 10.46960/2658-6754_2023_2_78].
Схема фиг. 1 включает следующие обозначения: 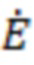 ′C,
′C, 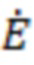 ′′C и Z′C, Z′′C - соответственно ЭДС и сопротивления систем (С1 и С2) по концам воздушной ЛЭП;
′′C и Z′C, Z′′C - соответственно ЭДС и сопротивления систем (С1 и С2) по концам воздушной ЛЭП;  ′КС,
′КС, 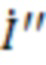 КС и Z′КС, Z′′КС - соответственно токи и сопротивления заземляющих устройств С1 и С2;
КС и Z′КС, Z′′КС - соответственно токи и сопротивления заземляющих устройств С1 и С2;  ′ ,
′ , 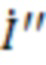 и Z′Л , Z′′Л - соответственно токи и сопротивления участков поврежденной воздушной ЛЭП;
и Z′Л , Z′′Л - соответственно токи и сопротивления участков поврежденной воздушной ЛЭП;  ′ГТ,
′ГТ, 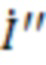 ГТ и Z′ГТ, Z′′ГТ - соответственно токи и сопротивления ГТ;
ГТ и Z′ГТ, Z′′ГТ - соответственно токи и сопротивления ГТ;  ′ЗУ,
′ЗУ, 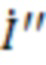 ЗУ и Z′ЗУ , Z′′ЗУ - соответственно токи и сопротивления заземляющих устройств опор; ZЗУ - сопротивление заземляющего устройства опоры в месте КЗ;
ЗУ и Z′ЗУ , Z′′ЗУ - соответственно токи и сопротивления заземляющих устройств опор; ZЗУ - сопротивление заземляющего устройства опоры в месте КЗ;  КЗ и RД - соответственно ток КЗ и сопротивление электрической дуги в месте КЗ.
КЗ и RД - соответственно ток КЗ и сопротивление электрической дуги в месте КЗ.
Согласно схеме (фиг. 1) при повреждении воздушной ЛЭП, соответствующим однофазному дуговому перекрытию изоляции на тело опоры, путь протекания тока от точки короткого замыкания (КЗ) до точек нулевого потенциала проходит через сопротивление электрической дуги, сопротивления контуров заземления опор и сопротивления ГТ. Очевидно, что при этом сопротивление повреждения имеет реактивную составляющую.
Для проведения имитационных экспериментов была реализована модель в программном комплексе MATLAB, которая представлена на фиг. 2.
Модель (фиг. 2) представляет собой воздушную ЛЭП 110 кВ, разделенную на 10 равных участков, соответствующих анкерным пролётам. Были заданы следующие параметры ЛЭП 110 кВ: протяженность 100 км, марка провода АС 150/24, тип промежуточных опор П110-3, грозотрос марки С-70, который по всей длине на опорах заземлён через искровые промежутки (ИП), а на концевых опорах заземлён наглухо.
Расчетная матрица погонных продольных сопротивлений ЛЭП в фазных координатах соответствует численным значениям:
 , Ом/км.
, Ом/км.
Сопротивление системы в начале ЛЭП (фиг. 2) [Висящев А.Н., Пленков Э.Р., Федосов Д.С. Оценка величины и характера переходного сопротивления в месте короткого замыкания на воздушных линиях электропередачи высокого напряжения // Интеллектуальная Электротехника. 2023. № 2. С. 78-89. DOI: 10.46960/2658-6754_2023_2_78] принято чисто индуктивным Z′C =0+j30 Ом, а в конце воздушной ЛЭП - чисто активным Z′′C =30+j0 Ом. Сопротивление электрической дуги в месте КЗ и контур заземлений опор приняты чисто активными: RД = 5 Ом и ZЗУ = 10+ j0 Ом соответственно. Емкостные проводимости воздушной ЛЭП не учитывались.
С использованием модели (фиг. 2) была проводилась имитация серии однофазных КЗ на расстоянии 20 км, 50 км, 80 км от начала воздушной ЛЭП 110 кВ для следующих вариантов заземления ГТ:
1. ГТ на концевых опорах заземлён наглухо, на остальных опорах заземлён через ИП, при этом в месте КЗ не пробит ИП (соответствует изолированному ГТ по всей длине ЛЭП).
2. ГТ на концевых опорах заземлён наглухо, на остальных опорах заземлён через ИП, при этом в месте КЗ пробит ИП.
3. ГТ на концевых и анкерных опорах заземлён наглухо, при этом в месте КЗ пробит ИП (или КЗ на анкерной опоре). Такое состояние имитационной модели воздушной ЛЭП также соответствует состоянию, когда ГТ по всей длине ЛЭП заземлён наглухо.
Таким образом, различные варианты протекания аварийного тока по заземленному ГТ, а также конструкции опор, при учете неоднородного сопротивления земли создают условия для появления реактивной составляющей сопротивления повреждения.
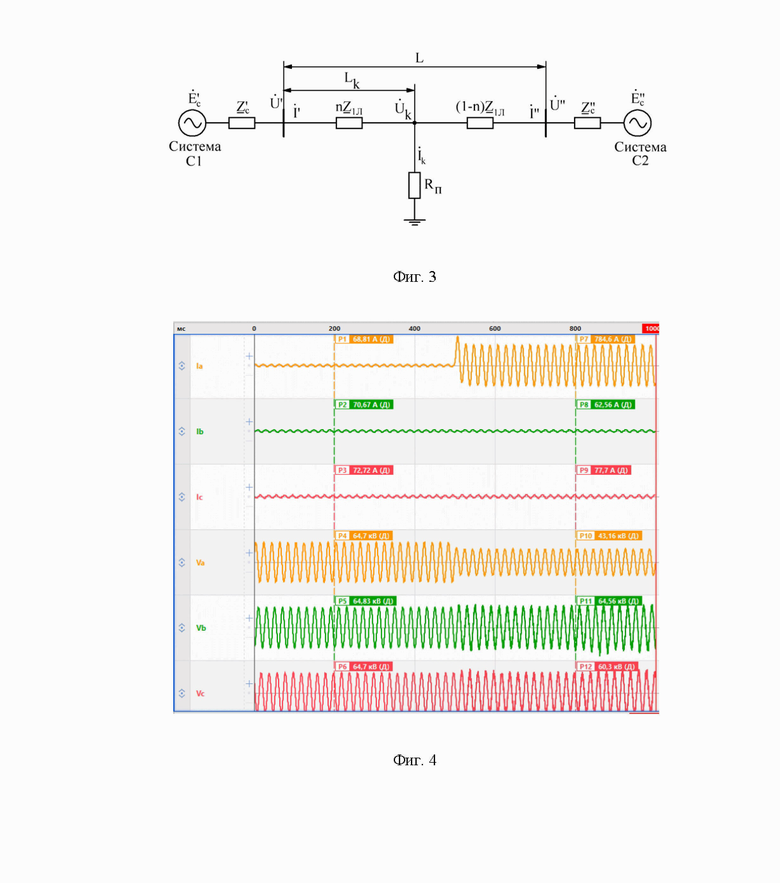
Расчет ошибок ОМП ЛЭП при наличии реактивной составляющей сопротивления повреждения выполним с учетом схемы замещения ЛЭП представленной на фиг. 3.
На схеме (фиг. 3) приведены следующие обозначения: 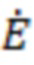 ′C,
′C, 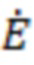 ′′C и Z′C, Z′′C - соответственно ЭДС и сопротивления систем (С1 и С2) по концам воздушной ЛЭП;
′′C и Z′C, Z′′C - соответственно ЭДС и сопротивления систем (С1 и С2) по концам воздушной ЛЭП;  ′,
′, 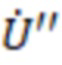 - напряжения на шинах систем С1 и С2;
- напряжения на шинах систем С1 и С2;  ′,
′, 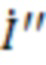 - токи участков поврежденной ЛЭП; n - относительное расстояние до места повреждения; Z1Л - полное сопротивление линии; Lk, L - соответственно расстояние до места повреждения и полная длина ЛЭП;
- токи участков поврежденной ЛЭП; n - относительное расстояние до места повреждения; Z1Л - полное сопротивление линии; Lk, L - соответственно расстояние до места повреждения и полная длина ЛЭП; 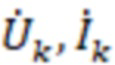 - напряжение и ток в месте повреждения; RП - переходное сопротивление в месте КЗ.
- напряжение и ток в месте повреждения; RП - переходное сопротивление в месте КЗ.
Поскольку путь протекания тока от точки КЗ до точек нулевого потенциала проходит через сопротивление электрической дуги, сопротивления контуров заземления опор и сопротивления ГТ (рис. 1), то сопротивление повреждения в месте КЗ может быть определено по выражению [Висящев А.Н., Пленков Э.Р., Федосов Д.С. Оценка величины и характера переходного сопротивления в месте короткого замыкания на воздушных линиях электропередачи высокого напряжения // Интеллектуальная Электротехника. 2023. №2. С. 78-89. DOI: 10.46960/2658-6754_2023_2_78]:
Z П = RД + ZЗУ⋅ZЭКВ / (ZЗУ + ZЭКВ), (3)
где ZЭКВ - эквивалентное сопротивление ГТ и заземляющих устройств опор воздушной ЛЭП относительно точки КЗ.
Приведем пример расчета для КЗ, соответствующего варианту 3 заземления ГТ, то есть на концевых и анкерных опорах ГТ заземлён наглухо, при этом в месте КЗ пробит ИП. Примем фактическое расстояние до точки КЗ LК.факт = 50 км (табл. 1). Считаем, что осциллограммы токов и напряжений в месте установки защиты, полученные с помощью имитационной модели (фиг. 2), соответствуют фиг. 4. На осциллограммах указаны действующие значения токов и напряжений для доаварийного (отметка 200 мс) и аварийного (отметка 800 мс) режимов.
По осциллограммам (фиг. 4) с учетом повреждения фазы «А» определяем численные значения комплексов токов и напряжений промышленной частоты, например, с помощью дискретного преобразования Фурье, необходимые для проведения расчетов. Учитываем, что в процессе определения сопротивления повреждения участвует в качестве расчетного способ-прототип («L - метр»).
Используем выражение (2) и полагаем, что ток в месте повреждения может быть выражен через чисто аварийный ток, тогда:
LК = Im [ А/
А/ ОП] / Im [Z1уд.Л⋅(
ОП] / Im [Z1уд.Л⋅( А + К⋅
А + К⋅ 0) /
0) / ОП]. (4)
ОП]. (4)
Согласно фиг. 4 необходимые для расчетов величины принимают следующие численные значения:  А = 60460 - j⋅8420,1 (В);
А = 60460 - j⋅8420,1 (В);  А = 541,86 - j⋅968,25 (А);
А = 541,86 - j⋅968,25 (А);  В = 82,315+ j⋅31,792 (А);
В = 82,315+ j⋅31,792 (А);  С = -35,265 + j⋅103,87 (А);
С = -35,265 + j⋅103,87 (А);  0 = (
0 = ( А+
А+ В+
В+ С)/3 = 196,30 - j⋅298,72 (А);
С)/3 = 196,30 - j⋅298,72 (А);  ОП =
ОП =  1ав =
1ав =  1 -
1 -  1доав = 466,68 - j⋅1030 (А).
1доав = 466,68 - j⋅1030 (А).
Учитывая численные значения удельных сопротивлений прямой и нулевой последовательностей воздушной ЛЭП: Z1уд.Л = Z1Л / L = 0,204 + j⋅0,428 (Ом) и Z0уд.Л = Z0Л / L = 0,346 + j⋅1,373 (Ом), получим коэффициент:
К = (Z0уд.Л - Z1уд.Л) / Z1уд.Л = 1,928 + j⋅0,588.
Выбирая способ-прототип ОМП ЛЭП («L - метр») производим расчет расстояния до места повреждения LК. В соответствии с параметрами осциллограмм расчет по способу-прототипу приводит к результату LК = 62, 082 (км). Затем по соотношениям напряжения и тока в поврежденной фазе определим переходное сопротивление ZП в месте повреждения. Исходим из того, что напряжение поврежденной фазы «А» в месте замера равно:
 А = LК⋅Z1уд.Л⋅(
А = LК⋅Z1уд.Л⋅( А + К⋅
А + К⋅ 0) + ZП⋅Кток⋅
0) + ZП⋅Кток⋅ 1ав,
1ав,
где Кток - коэффициент токораспределения равен:
К ток = [Z′C + L⋅Z1уд.Л + Z′′C] / [(L - LК)⋅Z1уд.Л + Z′′C],
где L - длина линии электропередачи; Z′C и Z′′C - сопротивления систем (С1 и С2) по концам воздушной ЛЭП (фиг. 3).
Таким образом, сопротивление повреждения ZП будет определяться выражением:
Z
П = [ А - LК⋅Z1уд.Л⋅(
А - LК⋅Z1уд.Л⋅( А + К⋅
А + К⋅ 0)] / Кток⋅
0)] / Кток⋅ 1ав. (5)
1ав. (5)
Подстановка ранее полученных численных значений в выражение (5) приводит к результату:
Z П = 11,556 - j⋅0,889 (Ом).
Результаты имитационного моделирования с использованием схемы воздушной ЛЭП (фиг. 2) при различных сопротивлениях и расстояниях до места повреждения приведены в таблице 1.
Таблица 1 - Расчётное расстояние до точки КЗ, полученное по способу-прототипу («L-метр»).
Анализ таблицы 1 показывает, что способ-прототип имеет значительные ошибки ОМП ЛЭП при наличии реактивной составляющей сопротивления повреждения. Например, для варианта 1 заземления ГТ при LК.факт = 80 (км) относительная ошибка способа-прототипа составила ΔLК = [(120,996 - 80)/100]⋅100% = 40,996%. Такие значительные ошибки ОМП ЛЭП не соответствуют требованиям эксплуатационной практики.
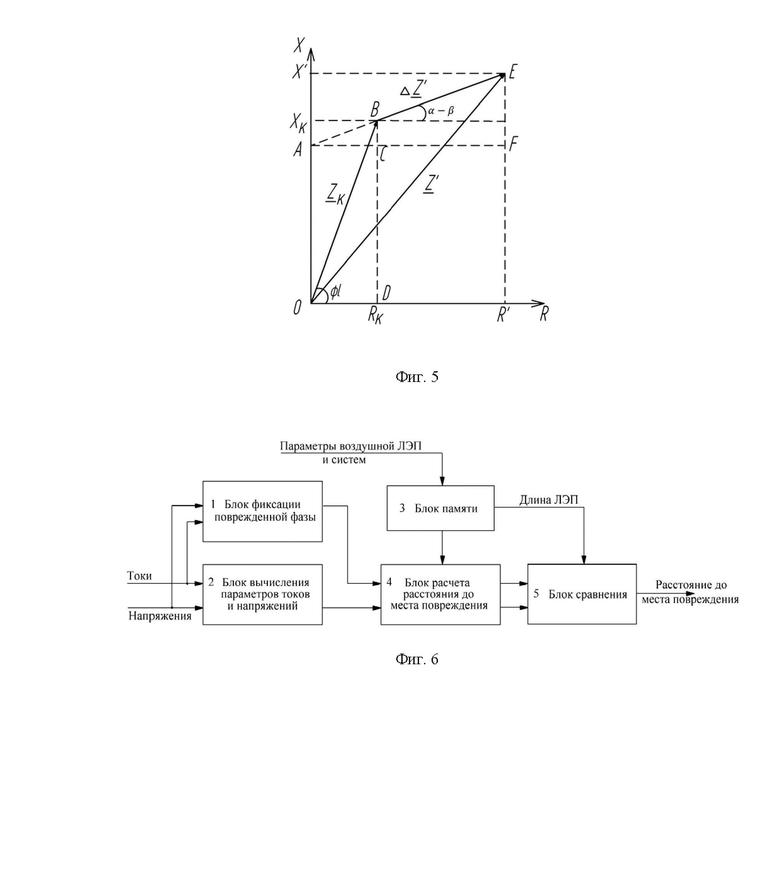
При изложении метода Аржанникова в [Аржанников Е. А. Определение места короткого замыкания на высоковольтных линиях электропередачи / Е. А. Аржанников, В. Ю. Лукоянов, М. Ш. Мисриханов; под ред. В. А. Шуина. - М.: Энергоатомиздат, 2003. - 272 с. (стр. 60-62, рис. 2.11)] вводилось понятие опорного тока  оп, по фазе наиболее близкого к току в месте повреждения
оп, по фазе наиболее близкого к току в месте повреждения  K (фиг. 5). Разность фаз β (иначе называемая углом коррекции) между
K (фиг. 5). Разность фаз β (иначе называемая углом коррекции) между  оп и
оп и  K не зависит от ЭДС в схеме замещения и величины переходного сопротивления. Таким образом, если вычислить угол коррекции и повернуть на него опорный ток, можно обеспечить полную компенсацию влияния переходного сопротивления на ошибки ОМП воздушных ЛЭП по ПАР. Предложенная реализация способа расчета расстояния до места повреждения ЛЭП будет соответствовать устойчивому методу ОМП, поскольку предполагается полная независимость результатов расчетов от величины и характера сопротивления повреждения.
K не зависит от ЭДС в схеме замещения и величины переходного сопротивления. Таким образом, если вычислить угол коррекции и повернуть на него опорный ток, можно обеспечить полную компенсацию влияния переходного сопротивления на ошибки ОМП воздушных ЛЭП по ПАР. Предложенная реализация способа расчета расстояния до места повреждения ЛЭП будет соответствовать устойчивому методу ОМП, поскольку предполагается полная независимость результатов расчетов от величины и характера сопротивления повреждения.
Введем понятие компенсирующего тока, который по фазе равен току в месте повреждения с учетом аргумента β, то есть это опорный ток, повернутый на угол β:  комп =
комп =  оп⋅e j·β, где
оп⋅e j·β, где  оп - опорный ток, который выбирают равным
оп - опорный ток, который выбирают равным  0,
0,  1ав или
1ав или  2, а β - фаза коэффициента токораспределения соответствующей последовательности.
2, а β - фаза коэффициента токораспределения соответствующей последовательности.
Для формирования устойчивого к величине и характеру сопротивления повреждения ЛЭП способа ОМП по ПАР выберем для модификации способ-прототип (выражение (2)), расчетное соотношение которого приобретает вид:
LК = Im[ ф / (
ф / ( оп⋅e j⋅β)] / Im[(
оп⋅e j⋅β)] / Im[( ф + K⋅
ф + K⋅ 0)⋅Z1Л / (
0)⋅Z1Л / ( оп⋅e j⋅β)], (6)
оп⋅e j⋅β)], (6)
где  ф - напряжение в поврежденной фазе;
ф - напряжение в поврежденной фазе;  ф - ток поврежденной фазы в месте замера; К = (Z0уд.Л - Z1уд.Л) / Z1уд.Л.
ф - ток поврежденной фазы в месте замера; К = (Z0уд.Л - Z1уд.Л) / Z1уд.Л.
Представим выражение (6) в виде:
LК = Im[G⋅e j⋅ψ⋅e -j·β)] / Im[C⋅e j⋅δ⋅e -j·β], (7)
где составляющие выражения (7) равны:
G⋅e j⋅ψ =  ф/
ф/  оп; C⋅e j⋅δ = (
оп; C⋅e j⋅δ = ( ф + K⋅
ф + K⋅ 0)⋅Z1Л /
0)⋅Z1Л /  оп. (8)
оп. (8)
Введем следующие преобразования:
LК = (G/C)⋅{Im[e j⋅ψ⋅e -j·β]}/{Im[C⋅e j⋅δ⋅e-j⋅β]}=(G/C)⋅{Im[Cos(ψ-β)+j⋅Sin( ψ -⋅β)]}/
{Im[Cos(δ-β)+j⋅Sin(δ-⋅β)]} = (G/C)⋅{Sin( ψ-⋅β)/Sin(δ-⋅β)}= (G/C)⋅[Sin(ψ)⋅Cos(β) -
Cos(ψ)Sin(β)]/[Sin(δ)⋅Cos(β) - Cos(δ)⋅Sin(β)] = (G/C)⋅Cos(β)⋅[Sin(ψ)⋅- Cos(ψ)⋅tg(β)]/
{Cos(β)⋅[Sin(δ) - Cos(δ)⋅tg(β)]} = {G⋅Sin(ψ)⋅- G⋅Cos(ψ)⋅tg(β)}/{C⋅Sin(δ) - C⋅Cos(δ)⋅tg(β)} =
{Im[G] - Re[G] tg(β)}/{Im[C] - Re[C] tg(β)}.
Таким образом,
LК⋅{Im[C] - Re[C] tg(β)} = {Im[G] - Re[G] tg(β)}, (9)
или
LК⋅Im[C] - LК⋅Re[C] tg(β) + Re[G] tg(β) - Im[G] = 0. (10)
Следует отметить, что угол коррекции β является аргументом коэффициента токораспределения:
β(LК) = arg [Kток(LК)], (11)
где
K ток(LК) = [Z′C + L⋅Z1уд.Л + Z′′C]/[(L - LК)⋅Z1уд.Л + Z′′C] =
[Rсум + j⋅Хсум]/[R′′C + (L - LК)⋅R1уд.Л + j⋅(Х′′C + (L - LК)⋅Х1уд.Л)], (12)
где Rсум = Re[Z′C + L⋅Z1уд.Л + Z′′C]; Хсум = Im[Z′C + L⋅Z1уд.Л + Z′′C]; Z′C = R′C + j⋅Х′C и Z′′C = R′′C + j⋅Х′′C - комплексные сопротивления систем, подключенных к концам по воздушной ЛЭП.
Умножим числитель и знаменатель дроби Kток(LК) (12) на выражение, комплексно-сопряженное со знаменателем. Таким образом, знаменатель дроби будет действительным числом, тогда фаза Kток(LК) будет определяться числителем, а ее тангенс соответствует выражению:
tg(β(LК)) = Im [числитель Kток(LК)]/Re [числитель Kток(LК)]. (13)
Учитывая структуру выражения (12), представим tg(β) в следующем виде:
tg(β(LК)) = [а1 +(L - LК)⋅b1]/[а2 + (L - LК)⋅b2], (14)
где а1 = R′′C⋅Хсум - Rсум⋅Х′′C; а2 = R′′C⋅Rсум + Rсум⋅Х′′C; b1 = R1уд.Л⋅Хсум - Rсум⋅Х1уд.Л; b2 = R1уд.Л Rсум - Xсум⋅Х1уд.Л.
Подставляем выражение (14) для tg(β(LК)) в выражение (10) и получаем:
LК⋅Im[C] + (Re[G] - LК⋅Re[C])⋅[а1 + (L - LК)⋅b1]/[а2 + (L - LК)⋅b2] - Im[G] = 0. (15)
Преобразуем выражение (15) к форме квадратного уравнения вида:
u⋅(LК)2 + v⋅(LК) + q = 0, (16)
где u = Re[C]⋅b1 - Im[C]⋅b2; v = Im[C]⋅(а2 + L⋅b2) - Re[C]⋅(а1 + L⋅b1) - Re[G]⋅b1 + Im[G]⋅b2;
q = Re[G]⋅(а1 + L⋅b1) - Im[G]⋅(а2 + L⋅b2).
Учитывая ранее введенные обозначения, коэффициенты квадратного уравнения (16) могут быть выражены следующим образом:
u = Re[( + K⋅
+ K⋅ 0)⋅Z1Л /
0)⋅Z1Л /  оп]⋅[R1уд.Л ⋅(Х′C+ L⋅X1уд.Л+ Х′′C) - (R′C+ L⋅R1уд.Л+ R′′C)⋅X1уд.Л] -
оп]⋅[R1уд.Л ⋅(Х′C+ L⋅X1уд.Л+ Х′′C) - (R′C+ L⋅R1уд.Л+ R′′C)⋅X1уд.Л] -
- Im[( + K⋅
+ K⋅ 0)⋅Z1Л /
0)⋅Z1Л /  оп]⋅[R1уд.Л ⋅(R′C + L⋅R1уд.Л + R′′C) - (Х′C+ L⋅X1уд.Л+ Х′′C)⋅X1уд.Л];
оп]⋅[R1уд.Л ⋅(R′C + L⋅R1уд.Л + R′′C) - (Х′C+ L⋅X1уд.Л+ Х′′C)⋅X1уд.Л];
v = Im[( + K·
+ K· 0)·Z1Л /
0)·Z1Л /  оп]⋅[(R′′C ⋅{R′C + L⋅R1уд.Л+ R′′C} + {R′C + L⋅R1уд.Л+ R′′C}⋅Х′′C) +
оп]⋅[(R′′C ⋅{R′C + L⋅R1уд.Л+ R′′C} + {R′C + L⋅R1уд.Л+ R′′C}⋅Х′′C) +
+ L⋅(R1уд.Л ⋅{R′C +L⋅R1уд.Л +R′′C}-{Х′C+L⋅X1уд.Л+Х′′C}⋅X1уд.Л)]-Re[( + K⋅
+ K⋅ 0)⋅Z1Л/
0)⋅Z1Л/ оп]⋅[(R′′C⋅{Х′C+ + L⋅X1уд.Л+ Х′′C} - {R′C + L⋅R1уд.Л+ R′′C} ⋅ Х′′C) + L⋅(R1уд.Л ⋅{Х′C+ L⋅X1уд.Л+ Х′′C} - {R′C+ L⋅R1уд.Л+ + R′′C}⋅X1уд.Л)] - Re[
оп]⋅[(R′′C⋅{Х′C+ + L⋅X1уд.Л+ Х′′C} - {R′C + L⋅R1уд.Л+ R′′C} ⋅ Х′′C) + L⋅(R1уд.Л ⋅{Х′C+ L⋅X1уд.Л+ Х′′C} - {R′C+ L⋅R1уд.Л+ + R′′C}⋅X1уд.Л)] - Re[ /
/  оп]⋅[ R1уд.Л ⋅(Х′C+ L⋅X1уд.Л + Х′′C) - (R′C+ L⋅R1уд.Л+ R′′C)⋅X1уд.Л] +
оп]⋅[ R1уд.Л ⋅(Х′C+ L⋅X1уд.Л + Х′′C) - (R′C+ L⋅R1уд.Л+ R′′C)⋅X1уд.Л] +
+ Im[ /
/  оп]⋅[R1уд.Л ⋅(R′C + L⋅R1уд.Л + R′′C) - (Х′C+ L⋅X1уд.Л+ Х′′C)⋅X1уд.Л];
оп]⋅[R1уд.Л ⋅(R′C + L⋅R1уд.Л + R′′C) - (Х′C+ L⋅X1уд.Л+ Х′′C)⋅X1уд.Л];
q = Re[ /
/  оп]⋅[(R′′C⋅{Х′C+ L⋅X1уд.Л+ Х′′C} - {R′C + L⋅R1уд.Л+ R′′C}⋅Х′′C) + L⋅(R1уд.Л⋅{Х′C+ + L⋅X1уд.Л+ Х′′C} - {R′C+ L⋅R1уд.Л+ R′′C}⋅X1уд.Л)] - Im[
оп]⋅[(R′′C⋅{Х′C+ L⋅X1уд.Л+ Х′′C} - {R′C + L⋅R1уд.Л+ R′′C}⋅Х′′C) + L⋅(R1уд.Л⋅{Х′C+ + L⋅X1уд.Л+ Х′′C} - {R′C+ L⋅R1уд.Л+ R′′C}⋅X1уд.Л)] - Im[ /
/  оп]⋅[(R′′C⋅{R′C + L⋅R1уд.Л+ R′′C}+{R′C + + L⋅R1уд.Л+ R′′C}⋅Х′′C) + L⋅(R1уд.Л⋅{R′C + L⋅R1уд.Л + R′′C} - {Х′C+ L⋅X1уд.Л+ Х′′C}⋅X1уд.Л)],
оп]⋅[(R′′C⋅{R′C + L⋅R1уд.Л+ R′′C}+{R′C + + L⋅R1уд.Л+ R′′C}⋅Х′′C) + L⋅(R1уд.Л⋅{R′C + L⋅R1уд.Л + R′′C} - {Х′C+ L⋅X1уд.Л+ Х′′C}⋅X1уд.Л)],
где  ,
,  - комплексные напряжения и ток поврежденной фазы;
- комплексные напряжения и ток поврежденной фазы;  оп - опорный ток;
оп - опорный ток;  0 - ток нулевой последовательности; Z1уд.Л = R1уд.Л+j⋅X1уд.Л - комплексное удельное сопротивление прямой последовательности ЛЭП; Z1Л = L⋅Z1уд.Л; L - длина воздушной ЛЭП; К - комплексный коэффициент компенсации тока нулевой последовательности, К = (Z0уд.Л - Z1уд.Л) / Z1уд.Л; Z0уд.Л - комплексное удельное сопротивление нулевой последовательности ЛЭП; Z′C = R′C + j⋅Х′C и Z′′C = R′′C + j⋅Х′′C - комплексные сопротивления систем (С1 и С2), подключенных к концам по воздушной ЛЭП.
0 - ток нулевой последовательности; Z1уд.Л = R1уд.Л+j⋅X1уд.Л - комплексное удельное сопротивление прямой последовательности ЛЭП; Z1Л = L⋅Z1уд.Л; L - длина воздушной ЛЭП; К - комплексный коэффициент компенсации тока нулевой последовательности, К = (Z0уд.Л - Z1уд.Л) / Z1уд.Л; Z0уд.Л - комплексное удельное сопротивление нулевой последовательности ЛЭП; Z′C = R′C + j⋅Х′C и Z′′C = R′′C + j⋅Х′′C - комплексные сопротивления систем (С1 и С2), подключенных к концам по воздушной ЛЭП.
Корень квадратного уравнения (16), лежащий в пределах воздушной ЛЭП, определяет расстояние до места повреждения:
LК1 = (- v + sqrt [v2 - 4⋅u⋅q])/2⋅u, или LК2 = (- v - sqrt [v2 - 4⋅u⋅q])/2⋅u (17)
где функция sqrt [⋅] - обозначает операцию извлечения квадратного корня.
Например, расчеты расстояния до места повреждения, выполненные по исходным данным рассмотренного выше примера (табл. 1, Вариант1, LК.факт = 80 км), свидетельствуют о высокой точности предложенного способа ОМП ЛЭП (17). Его реализация соответствует расстоянию до места повреждения LК = 80,864 (км), а относительная ошибка составила
ΔLК = [(80,835- 80)/100]⋅100%= 0,835%.
Результаты имитационных экспериментов с моделью (фиг. 2) для предложенного способа ОМП ЛЭП сведены в таблицу 2.
Таблица 2 - Расчётное расстояние до точки КЗ, полученное по предложенному способу ОМП ЛЭП.
Анализ таблицы 2 позволяет сделать следующие выводы:
- моделирование показало, что ошибки предложенного способа ОМП ЛЭП по ПАР для воздушных ЛЭП, имеющих заземленный ГТ, могут принимать как положительный, так и отрицательный характер;
- величина ошибок предложенного способа ОМП ЛЭП по ПАР практически не зависит от соотношения составляющих и величины сопротивления повреждения, что позволяет судит об устойчивости способа;
- расхождения между расчетным LК.расч и фактическим LК.факт местом повреждения не превышает одного процента, что свидетельствует о высокой точности предложенного способа ОМП ЛЭП по ПАР.
Таким образом, предложенный способ ОМП ЛЭП по ПАР обладает высокой точностью и устойчив не только к активной, но и к реактивной составляющей сопротивления повреждения.
Задача изобретения состоит в повышении точности определения расстояния до места повреждения на воздушных линиях электропередачи, оборудованных грозозащитным тросом.
Поставленная задача достигается способом определения места повреждения на воздушной линии электропередачи, оборудованной грозозащитным тросом, согласно которому производят определение поврежденной фазы линии электропередачи, измеряют фазные напряжения и токи аварийного и доаварийного режимов в начале линии электропередачи, определяют симметричные составляющие токов по измеренным фазным токам, определяют чисто аварийный ток прямой последовательности, как разность токов прямой последовательности аварийного и доаварийного режимов, в выражении для расчета расстояния до места повреждения используют опорный ток, в качестве которого выбирают ток нулевой, обратной последовательностей или чисто аварийный ток прямой последовательности.
Согласно предложения минимизируют влияние реактивной составляющей сопротивления повреждения на точность определения места повреждения воздушной линии электропередачи, оборудованной грозозащитным тросом, наряду с параметрами воздушной линии электропередачи дополнительно в памяти устройства, реализующего способ, хранят и используют в последующих расчетах информацию о параметрах сопротивлений присоединенных к линии электропередачи систем, для минимизации влияния реактивной составляющей сопротивления повреждения на точность определения места повреждения воздушной линии электропередачи реализуют расчет расстояния LК до места повреждения согласно квадратного уравнения:
u⋅(LК)2 + v⋅(LК) + q = 0,
где: u = Re[( + K⋅
+ K⋅ 0)⋅Z1Л /
0)⋅Z1Л /  оп]⋅[R1уд.Л ⋅(Х′C+ L⋅X1уд.Л+ Х′′C) - (R′C+ L⋅R1уд.Л+ R′′C)⋅X1уд.Л] -
оп]⋅[R1уд.Л ⋅(Х′C+ L⋅X1уд.Л+ Х′′C) - (R′C+ L⋅R1уд.Л+ R′′C)⋅X1уд.Л] -
- Im[( + K·
+ K· 0)⋅Z1Л /
0)⋅Z1Л /  оп]⋅[R1уд.Л ⋅(R′C + L⋅R1уд.Л + R′′C) - (Х′C+ L⋅X1уд.Л+ Х′′C)⋅X1уд.Л];
оп]⋅[R1уд.Л ⋅(R′C + L⋅R1уд.Л + R′′C) - (Х′C+ L⋅X1уд.Л+ Х′′C)⋅X1уд.Л];
v = Im[( + K⋅
+ K⋅ 0)⋅Z1Л /
0)⋅Z1Л /  оп]⋅[(R′′C ⋅{R′C + L⋅R1уд.Л+ R′′C} + {R′C + L⋅R1уд.Л+ R′′C}⋅Х′′C) +
оп]⋅[(R′′C ⋅{R′C + L⋅R1уд.Л+ R′′C} + {R′C + L⋅R1уд.Л+ R′′C}⋅Х′′C) +
+ L⋅(R1уд.Л ⋅{R′C +L⋅R1уд.Л +R′′C}-{Х′C+L⋅X1уд.Л+Х′′C}⋅X1уд.Л)]-Re[( + K⋅
+ K⋅ 0)·Z1Л/
0)·Z1Л/ оп]⋅[(R′′C⋅{Х′C+ + L⋅X1уд.Л+ Х′′C} - {R′C + L⋅R1уд.Л+ R′′C}⋅Х′′C) + L⋅(R1уд.Л ⋅{Х′C+ L⋅X1уд.Л+ Х′′C} - {R′C+ L⋅R1уд.Л+ + R′′C}⋅X1уд.Л)] - Re[
оп]⋅[(R′′C⋅{Х′C+ + L⋅X1уд.Л+ Х′′C} - {R′C + L⋅R1уд.Л+ R′′C}⋅Х′′C) + L⋅(R1уд.Л ⋅{Х′C+ L⋅X1уд.Л+ Х′′C} - {R′C+ L⋅R1уд.Л+ + R′′C}⋅X1уд.Л)] - Re[ /
/  оп]⋅[ R1уд.Л ⋅(Х′C+ L⋅X1уд.Л + Х′′C) - (R′C+ L⋅R1уд.Л+ R′′C)⋅X1уд.Л] +
оп]⋅[ R1уд.Л ⋅(Х′C+ L⋅X1уд.Л + Х′′C) - (R′C+ L⋅R1уд.Л+ R′′C)⋅X1уд.Л] +
+ Im[ /
/  оп]⋅[R1уд.Л ⋅(R′C + L⋅R1уд.Л + R′′C) - (Х′C+ L⋅X1уд.Л+ Х′′C)⋅X1уд.Л];
оп]⋅[R1уд.Л ⋅(R′C + L⋅R1уд.Л + R′′C) - (Х′C+ L⋅X1уд.Л+ Х′′C)⋅X1уд.Л];
q = Re[ /
/  оп]⋅[(R′′C⋅{Х′C+ L⋅X1уд.Л+ Х′′C} - {R′C + L⋅R1уд.Л+ R′′C}⋅Х′′C) + L⋅(R1уд.Л⋅{Х′C+ + L⋅X1уд.Л+ Х′′C} - {R′C+ L⋅R1уд.Л+ R′′C}⋅X1уд.Л)] - Im[
оп]⋅[(R′′C⋅{Х′C+ L⋅X1уд.Л+ Х′′C} - {R′C + L⋅R1уд.Л+ R′′C}⋅Х′′C) + L⋅(R1уд.Л⋅{Х′C+ + L⋅X1уд.Л+ Х′′C} - {R′C+ L⋅R1уд.Л+ R′′C}⋅X1уд.Л)] - Im[ /
/  оп]⋅[(R′′C⋅{R′C + L⋅R1уд.Л+ R′′C}+{R′C + + L⋅R1уд.Л+ R′′C}⋅Х′′C) + L⋅(R1уд.Л⋅{R′C + L⋅R1уд.Л + R′′C} - {Х′C+ L⋅X1уд.Л+ Х′′C}⋅X1уд.Л)];
оп]⋅[(R′′C⋅{R′C + L⋅R1уд.Л+ R′′C}+{R′C + + L⋅R1уд.Л+ R′′C}⋅Х′′C) + L⋅(R1уд.Л⋅{R′C + L⋅R1уд.Л + R′′C} - {Х′C+ L⋅X1уд.Л+ Х′′C}⋅X1уд.Л)];
 ,
,  - комплексные напряжения и ток поврежденной фазы;
- комплексные напряжения и ток поврежденной фазы;  оп - опорный ток;
оп - опорный ток;  0 - ток нулевой последовательности; Z1уд.Л = R1уд.Л+j⋅X1уд.Л - комплексное удельное сопротивление прямой последовательности линии электропередачи; Z1Л = L⋅Z1уд.Л; L - длина воздушной линии электропередачи; К - комплексный коэффициент компенсации тока нулевой последовательности, К = (Z0уд.Л - Z1уд.Л) / Z1уд.Л; Z0уд.Л - комплексное удельное сопротивление нулевой последовательности линии электропередачи; Z′C = R′C + j⋅Х′C и Z′′C = R′′C + j⋅Х′′C - комплексные сопротивления систем, подключенных к концам по воздушной линии электропередачи;
0 - ток нулевой последовательности; Z1уд.Л = R1уд.Л+j⋅X1уд.Л - комплексное удельное сопротивление прямой последовательности линии электропередачи; Z1Л = L⋅Z1уд.Л; L - длина воздушной линии электропередачи; К - комплексный коэффициент компенсации тока нулевой последовательности, К = (Z0уд.Л - Z1уд.Л) / Z1уд.Л; Z0уд.Л - комплексное удельное сопротивление нулевой последовательности линии электропередачи; Z′C = R′C + j⋅Х′C и Z′′C = R′′C + j⋅Х′′C - комплексные сопротивления систем, подключенных к концам по воздушной линии электропередачи;
решают квадратное уравнение, а его корни:
LК1 = (- v + sqrt [v2 - 4⋅u⋅q])/2⋅u, LК2 = (- v - sqrt [v2 - 4⋅u⋅q])/2⋅u,
проверяют в блоке сравнения устройства на возможное расположение в пределах воздушной линии электропередачи, значение корня квадратного уравнения, лежащего в пределах воздушной линии электропередачи, принимают за значение расстояния LК до места повреждения и с выхода блока сравнения передают на его выход устройства, реализующего способ.
На фиг. 1 представлена эквивалентная схема замещения воздушной ЛЭП с заземлённым наглухо грозозащитным тросом на концевых и анкерных опорах и с пробитым искровым промежутком в месте КЗ [Висящев А.Н., Пленков Э.Р., Федосов Д.С. Оценка величины и характера переходного сопротивления в месте короткого замыкания на воздушных линиях электропередачи высокого напряжения // Интеллектуальная Электротехника. 2023. № 2. С. 78-89. DOI: 10.46960/2658-6754_2023_2_78].
Схема фиг. 1 включает следующие обозначения: 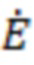 ′C,
′C, 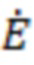 ′′C и Z′C, Z′′C - соответственно ЭДС и сопротивления систем (С1 и С2) по концам воздушной ЛЭП;
′′C и Z′C, Z′′C - соответственно ЭДС и сопротивления систем (С1 и С2) по концам воздушной ЛЭП;  ′КС,
′КС, 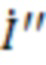 КС и Z′КС, Z′′КС - соответственно токи и сопротивления заземляющих устройств С1 и С2;
КС и Z′КС, Z′′КС - соответственно токи и сопротивления заземляющих устройств С1 и С2;  ′ ,
′ , 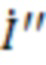 и Z′Л , Z′′Л - соответственно токи и сопротивления участков поврежденной ВЛ;
и Z′Л , Z′′Л - соответственно токи и сопротивления участков поврежденной ВЛ;  ′ГТ,
′ГТ, 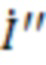 ГТ и Z′ГТ, Z′′ГТ - соответственно токи и сопротивления ГТ;
ГТ и Z′ГТ, Z′′ГТ - соответственно токи и сопротивления ГТ;  ′ЗУ,
′ЗУ, 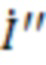 ЗУ и Z′ЗУ , Z′′ЗУ - соответственно токи и сопротивления заземляющих устройств опор; ZЗУ - сопротивление заземляющего устройства опоры в месте КЗ;
ЗУ и Z′ЗУ , Z′′ЗУ - соответственно токи и сопротивления заземляющих устройств опор; ZЗУ - сопротивление заземляющего устройства опоры в месте КЗ;  КЗ и RД - соответственно ток КЗ и сопротивление электрической дуги в месте КЗ.
КЗ и RД - соответственно ток КЗ и сопротивление электрической дуги в месте КЗ.
На фиг. 2 изображена модель воздушной ЛЭП 110 кВ, выполненная в программном комплексе MATLAB.
На фиг. 3 представлена схема замещения поврежденной воздушной ЛЭП.
На схеме (фиг. 3) приведены следующие обозначения: 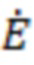 ′C,
′C, 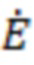 ′′C и Z′C, Z′′C - соответственно ЭДС и сопротивления систем (С1 и С2) по концам ЛЭП;
′′C и Z′C, Z′′C - соответственно ЭДС и сопротивления систем (С1 и С2) по концам ЛЭП;  ′,
′, 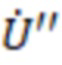 - напряжения на шинах систем С1 и С2;
- напряжения на шинах систем С1 и С2;  ′,
′, 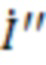 - токи участков поврежденной ЛЭП; n - относительное расстояние до места повреждения; Z1Л - полное сопротивление линии; Lk, L - соответственно расстояние до места повреждения и полная длина ЛЭП;
- токи участков поврежденной ЛЭП; n - относительное расстояние до места повреждения; Z1Л - полное сопротивление линии; Lk, L - соответственно расстояние до места повреждения и полная длина ЛЭП; 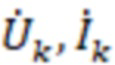 - напряжение и ток в месте повреждения; RП - переходное сопротивление в месте КЗ.
- напряжение и ток в месте повреждения; RП - переходное сопротивление в месте КЗ.
На фиг. 4 изображены осциллограммы токов и напряжений при КЗ на воздушной ЛЭП.
На фиг. 5 представлена диаграмма сопротивлений к пояснению принципа компенсации ошибки по методу Аржанникова.
На фиг.6 приведен вариант структурной схема устройства, реализующего предложенный способ определения места повреждения на воздушной линии электропередачи, оборудованной грозозащитным тросом.
Устройство (фиг. 6) включает: блок 1 фиксации поврежденной фазы; блок 2 вычисления параметров токов и напряжений; блок 3 памяти; блок 4 расчета расстояния до места повреждения; блок 5 сравнения.
Устройство (фиг. 6), реализующее предложенный способ определения места повреждения на воздушной линии электропередачи, оборудованной грозозащитным тросом, работает следующим образом.
Перед началом работы устройства (фиг. 6) в блок 3 памяти записываются значения параметров воздушной линии электропередачи, а также информация о параметрах комплексных сопротивлений, присоединенных к линии электропередачи систем. Объем информации, требуемой для записи в блок 3, определяется коэффициентами u, v, q, входящими в состав квадратного уравнения (16).
При однофазном КЗ на защищаемой воздушной ЛЭП на основе поступающих мгновенных значений токов и напряжений аварийного режима блок 1 фиксации поврежденной фазы определяет поврежденную фазу воздушной ЛЭП и выдает эту информацию на первый вход блока 4 расчета расстояния до места повреждения.
Параллельно в блоке 2 по мгновенным значениям фазных токов и напряжений осуществляется измерение (оценка параметров) комплексных значений фазных токов и напряжений, а также их симметричных составляющих. Комплексные значения фазных токов и напряжений, а также их симметричных составляющих с выхода блока 2 вычисления параметров токов и напряжений подают на второй вход блока 4 расчета расстояния до места повреждения. На третий вход блока 4 из блока 3 памяти поступают параметры воздушной ЛЭП и систем, необходимые для расчета расстояния до места повреждения.
В блоке 4 осуществляется расчет расстояний до места повреждения по выражениям (17) с получением численных значений LК1 и LК2, соответствующих корням квадратного уравнения (16). Численные значения LК1 и LК2 с первого и второго выходов блока 4 передаются на соответствующие входы блока 5 сравнения. На третий вход блока 5 сравнения поступает информация о длине воздушной ЛЭП. Сравнение информации о длине воздушной ЛЭП и значений корней квадратного уравнения LК1 и LК2, лежащих в пределах воздушной ЛЭП, обеспечивает определение расстояния до места повреждения. Информация о расстоянии до места повреждения с выхода блока 5 сравнения передается на выход устройства, реализующего способ.
Таким образом, реализация расчетов расстояния до места повреждения на основе квадратного уравнения (16) позволяет минимизировать влияние реактивной составляющей сопротивления повреждения на точность определения места повреждения и тем самым обеспечить решение задачи изобретения, состоящей в повышении точности определения расстояния до места повреждения на воздушных линиях электропередачи, оборудованных грозозащитным тросом.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения места повреждения линий электропередачи | 2024 |
|
RU2832411C1 |
| Способ определения места короткого замыкания на воздушной линии электропередачи по замерам с двух ее концов | 2022 |
|
RU2801352C1 |
| Способ определения мест повреждения (ОМП) межподстанционной зоны тягового электроснабжения 2х25 кВ | 2022 |
|
RU2788303C1 |
| Способ определения места повреждения на воздушной линии электропередачи по замерам токов с двух ее концов | 2023 |
|
RU2823691C1 |
| Способ определения места повреждения разветвленной линии электропередачи с несколькими источниками питания | 2020 |
|
RU2732796C1 |
| Способ определения места короткого замыкания на воздушной линии электропередачи при несинхронизированных замерах с двух ее концов | 2022 |
|
RU2793555C1 |
| Способ определения места короткого замыкания на воздушной линии электропередачи при несинхронизированных замерах с двух ее концов | 2023 |
|
RU2813463C1 |
| Способ определения места повреждения на воздушной линии электропередачи по замерам токов с двух ее концов | 2023 |
|
RU2828439C1 |
| СПОСОБ ДИСТАНЦИОННОГО ОПРЕДЕЛЕНИЯ МЕСТА КОРОТКОГО ЗАМЫКАНИЯ | 2018 |
|
RU2700370C1 |
| Способ определения места повреждения на воздушной линии электропередачи при замерах с двух ее концов | 2023 |
|
RU2816200C1 |
Изобретение относится к электроэнергетике и может быть использовано для определения места повреждения на воздушных линиях электропередачи, оборудованных грозозащитным тросом по всей длине. Технический результат: повышение точности определения расстояния до места повреждения на воздушных линиях электропередачи, оборудованных грозозащитным тросом. Сущность: производят определение поврежденной фазы линии электропередачи, измеряют фазные напряжения и токи аварийного и доаварийного режимов в начале линии электропередачи, определяют симметричные составляющие токов по измеренным фазным токам, определяют чисто аварийный ток прямой последовательности как разность токов прямой последовательности аварийного и доаварийного режимов. При расчете расстояния выбирают в качестве опорного тока ток нулевой, обратной последовательностей или чисто аварийный ток прямой последовательности. В памяти устройства, реализующего способ, наряду с параметрами воздушной линии электропередачи хранят и используют в последующих расчетах информацию о параметрах сопротивлений присоединенных к линии электропередачи систем. Минимизируют влияние реактивной составляющей сопротивления повреждения на точность определения места повреждения воздушной линии электропередачи при расчете расстояния до места повреждения путем решения квадратного уравнения. Корни квадратного уравнения проверяют в блоке сравнения на возможное расположение в пределах воздушной линии электропередачи. При этом значение корня квадратного уравнения, лежащего в пределах воздушной линии электропередачи, принимают за значение расстояния до места повреждения и с выхода блока сравнения передают его на выход устройства, реализующего способ. 6 ил., 2 табл.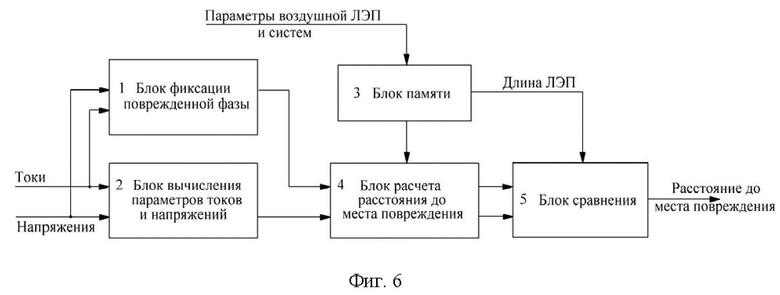
Способ определения места повреждения на воздушной линии электропередачи, оборудованной грозозащитным тросом, согласно которому производят определение поврежденной фазы линии электропередачи, измеряют фазные напряжения и токи аварийного и доаварийного режимов в начале линии электропередачи, определяют симметричные составляющие токов по измеренным фазным токам, определяют чисто аварийный ток прямой последовательности как разность токов прямой последовательности аварийного и доаварийного режимов, в выражении для расчета расстояния до места повреждения используют опорный ток, в качестве которого выбирают ток нулевой, обратной последовательностей или чисто аварийный ток прямой последовательности, отличающийся тем, что минимизируют влияние реактивной составляющей сопротивления повреждения на точность определения места повреждения воздушной линии электропередачи, оборудованной грозозащитным тросом, наряду с параметрами воздушной линии электропередачи дополнительно в памяти устройства, реализующего способ, хранят и используют в последующих расчетах информацию о параметрах сопротивлений присоединенных к линии электропередачи систем, для минимизации влияния реактивной составляющей сопротивления повреждения на точность определения места повреждения воздушной линии электропередачи реализуют расчет расстояния LK до места повреждения согласно квадратному уравнению:
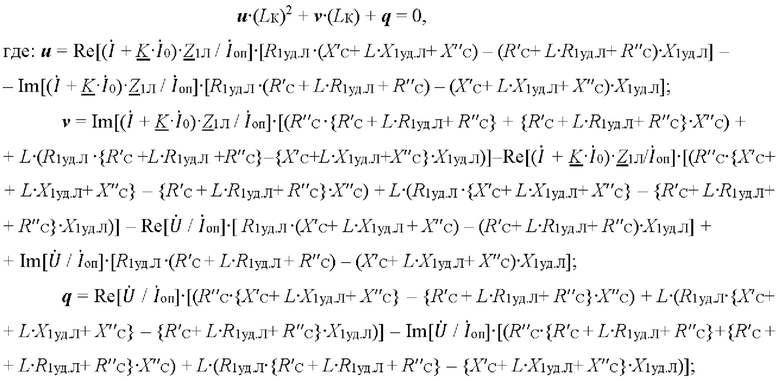
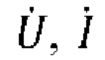 - комплексные напряжения и ток поврежденной фазы;
- комплексные напряжения и ток поврежденной фазы; 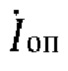 - опорный ток; i0 - ток нулевой последовательности;
- опорный ток; i0 - ток нулевой последовательности; 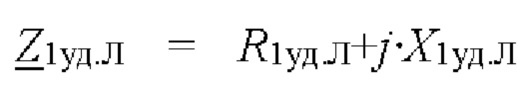 - комплексное удельное сопротивление прямой последовательности линии электропередачи;
- комплексное удельное сопротивление прямой последовательности линии электропередачи; 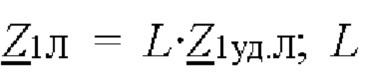 - длина воздушной линии электропередачи; K - комплексный коэффициент компенсации тока нулевой последовательности,
- длина воздушной линии электропередачи; K - комплексный коэффициент компенсации тока нулевой последовательности, 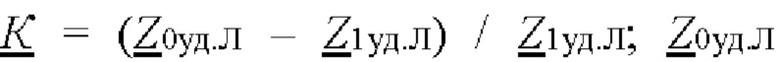 - комплексное удельное сопротивление нулевой последовательности линии электропередачи;
- комплексное удельное сопротивление нулевой последовательности линии электропередачи; 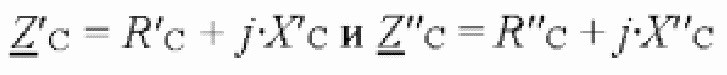 - комплексные сопротивления систем, подключенных к концам по воздушной линии электропередачи;
- комплексные сопротивления систем, подключенных к концам по воздушной линии электропередачи;
решают квадратное уравнение, а его корни:
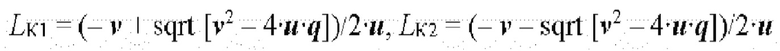
проверяют в блоке сравнения устройства на возможное расположение в пределах воздушной линии электропередачи, значение корня квадратного уравнения, лежащего в пределах воздушной линии электропередачи, принимают за значение расстояния LK до места повреждения и с выхода блока сравнения передают его на выход устройства, реализующего способ.
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТА ПОВРЕЖДЕНИЯ НА ВОЗДУШНЫХ И КАБЕЛЬНЫХ ЛИНИЯХ ЭЛЕКТРОПЕРЕДАЧИ В СЕТЯХ С ИЗОЛИРОВАННОЙ НЕЙТРАЛЬЮ | 2013 |
|
RU2539830C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТА ПОВРЕЖДЕНИЯ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ С ОДНОСТОРОННИМ ПИТАНИЕМ (ВАРИАНТЫ) | 1995 |
|
RU2116654C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТА ПОВРЕЖДЕНИЯ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ С ДВУСТОРОННИМ ПИТАНИЕМ | 1995 |
|
RU2107304C1 |
| Способ определения мест повреждения при коротких замыканиях на землю воздушных линий электропередачи | 1975 |
|
SU533886A1 |
| WO 1994009377 A1, 28.04.1994 | |||
| АРЖАННИКОВ Е.А | |||
| и др | |||
| Определение места короткого замыкания на высоковольтных линиях электропередачи, М., Энергоатомиздат, 2003, с | |||
| Способ очищения сернокислого глинозема от железа | 1920 |
|
SU47A1 |
Авторы
Даты
2025-02-13—Публикация
2024-08-29—Подача