Изобретение относится к области оптических измерений трехмерных координат объектов в пространстве, в частности к фото- и видеограмметрии, и может применяться в научных исследованиях, в машиностроении и в других областях для измерений координат точек поверхности объектов.
Из уровня техники известен способ оптических измерений геометрических параметров объекта в пространстве с помощью одной камеры и системы реперных точек, то есть меток, хорошо различимых на поверхности объекта (патент RU 2551396, МПК G01B 11/16 (2006.01), опубл. 20.05.2015), в котором на поверхности объекта в заданных точках наносят реперы, определяют параметры рабочей характеристики, измеряют на изображении двумерные координаты образов реперов, на основании заранее известных геометрических параметров объекта в пространстве на его поверхности выделяют обособленные зоны, для которых формируют собственную математическую параметрическую модель, одну из обособленных зон выделяют так, чтобы можно было считать точки ее поверхности взаимно неподвижными и, принимая ее за базовую, определяют для указанной зоны параметры взаимного расположения реперов в собственной системе координат и собственные параметры внешнего ориентирования, при этом при обработке из измеренных двумерных координат, параметров рабочей характеристики, собственных параметров внешнего ориентирования базовой зоны и математической параметрической модели методами многомерной численной минимизации находят искомые геометрические параметры модели.
Недостаток способа заключается в том, что он предполагает разделение объекта на части с известными геометрическими параметрами.
В качестве прототипа как наиболее близкий по совокупности признаков выбран способ измерений координат точек объекта в пространстве (патент RU 2749654, МПК G01B 11/16 (2006.01), опубл. 16.06.2021). Способ прототипа заключается в том, что на поверхности объекта размещают реперы, на участках ожидаемой минимальной деформации выделяют группу базовых реперов и определяют их начальные трехмерные координаты, находят параметры рабочей характеристики, при нагружении деформируемого объекта фиксируют изображение, на котором определяют двухмерные координаты образов всех реперов, с помощью найденных параметров рабочей характеристики находят искомые трехмерные координаты всех реперов. При этом реперы размещают в соответствии с заданными исходными геометрическими связями между ними, последовательно определяют прогнозируемые значения трехмерных координат реперов, используя при этом заданные геометрические связи и исходные трехмерные координаты базовых реперов и/или найденные трехмерные координаты реперов, следующих за базовыми реперами. Затем определяют прогнозируемые значения трехмерных координат каждого репера, производят уточнение трехмерных координат, для чего варьируют прогнозируемые координаты в пределах заданных геометрических связей, с использованием параметров рабочей характеристики в обращенной форме для каждой вариации координат вычисляют текущие значения двухмерных координат реперов, сопоставляют их с двухмерными координатами образов реперов на изображении и принимают за результирующие координаты текущего репера вариацию трехмерных координат, отвечающую максимуму критерия совпадения. Заявленным в способе прототипа техническим результатом является сокращение времени и объема вычислений при обработке изображений.
Из описания способа прототипа следует, что процедура уточнения прогнозируемых трехмерных координат с центром в прогнозируемой точке выполняется следующим образом:
- выделяют пространственный элемент объема (в описании прототипа - куб со сторонами 3 мм × 3 мм × 3 мм);
- куб разбивают на малые элементы (в описании прототипа - на подобные ему, т.е. кубы с меньшим размером ребра - 0,1 мм × 0,1 мм × 0,1 мм);
- геометрическому центру (X, Y, Z) каждого малого элемента с помощью рабочей характеристики видеограмметрической системы в обращенной форме ставят в соответствие двумерные координаты (u, v) на изображении, при этом рабочей характеристики видеограмметрической системы в обращенной форме представляет собой уравнения проекции для математической модели проективной камеры (Hartley R., Zisserman A. Multiple View Geometry in Computer Vision: 2nd ed. - Cambridge: Cambridge University Press, 2003. - 656 p.) без дисторсии при выборе системы координат камеры в качестве опорной;
- из множества проанализированных таким образом наборов (X, Y, Z, u, v) выбирают те значения трехмерных координат, которые минимизируют в пространстве двумерных координат (u, v) евклидово расстояние от центра образа соответственного репера на изображении; указанные значения и принимают за результирующие координаты текущего репера;
- аналогичные действия производят для каждого репера ряда и всех рядов, то есть для нахождения пространственных координат репера в ряду с номером i используют координаты реперов этого ряда с номерами (i-1) и (i-2).
Таким образом, процедура уточнения при разбиении пространственного элемента объема на n долей вдоль каждой пространственной координаты приводит к необходимости повторять вычисления для уравнений проективной геометрии n3 раз: так, для примера, приведенного в способе прототипа с n=3 мм / 0,1 мм=30, потребуется N=n3=303=27000 циклических вычислений.
В описании прототипа дополнительно отмечается, что для анализируемого объекта, жесткому вдоль оси, перпендикулярной плоскости ху изображения, деформациями вдоль данной оси можно пренебречь, что позволяет искать координаты репера не в пространстве, а в плоскости, что уменьшает время на обработку изображений. Действительно, для рассмотренного в описании прототипа примера объем циклических вычислений в таком случае уменьшится c N=n3 до N=n2=302=900.
По этой причине к недостатку способа прототипа следует отнести большой объем вычислений на реализацию процедуры уточнения прогнозируемых трехмерных координат.
Техническая проблема, решаемая заявляемым изобретением, заключается в избыточном объеме вычислений для реализации процедуры уточнения прогнозируемых трехмерных координат.
Технический результат изобретения заключается в разработке однократно выполняемой в каждом цикле измерения пространственных координат процедуры уточнения прогнозируемых трехмерных координат точки, не содержащей перебора всех ее возможных положений внутри пространственного элемента объема.
Технический результат достигается тем, что для уточнения трехмерных пространственных координат реперных точек применяются уравнения математической модели проективной камеры (Hartley R., Zisserman A. Multiple View Geometry in Computer Vision: 2nd ed. - Cambridge: Cambridge University Press, 2003. - 656 p.). При этом принимаются следующие ограничения на решение поставленной задачи:
1) объект с реперами имеет высокую жесткость вдоль своей продольной оси, т.е. не подвержен растяжению и/или сжатию при деформациях;
2) для регистрирующей реперы камеры с помощью одного из известных подходов предварительно выполнена процедура фотограмметрической калибровки, т.е. априори известна ее матрицы внутренних параметров K и коэффициенты, характеризующие дисторсию оптической системы камеры;
3) для пиксельных координат реперов после регистрации выполнена процедура компенсации дисторсии, например, согласно модели Брауна-Конради (Brown D.C. Close-range camera calibration // Photogrammetric Engineering. 1971. Vol. 37, No 8. P. 855-866);
4) в качестве базовой принята система координат камеры: ось X направлена вправо, ось Y - вниз, ось Z - вперед.
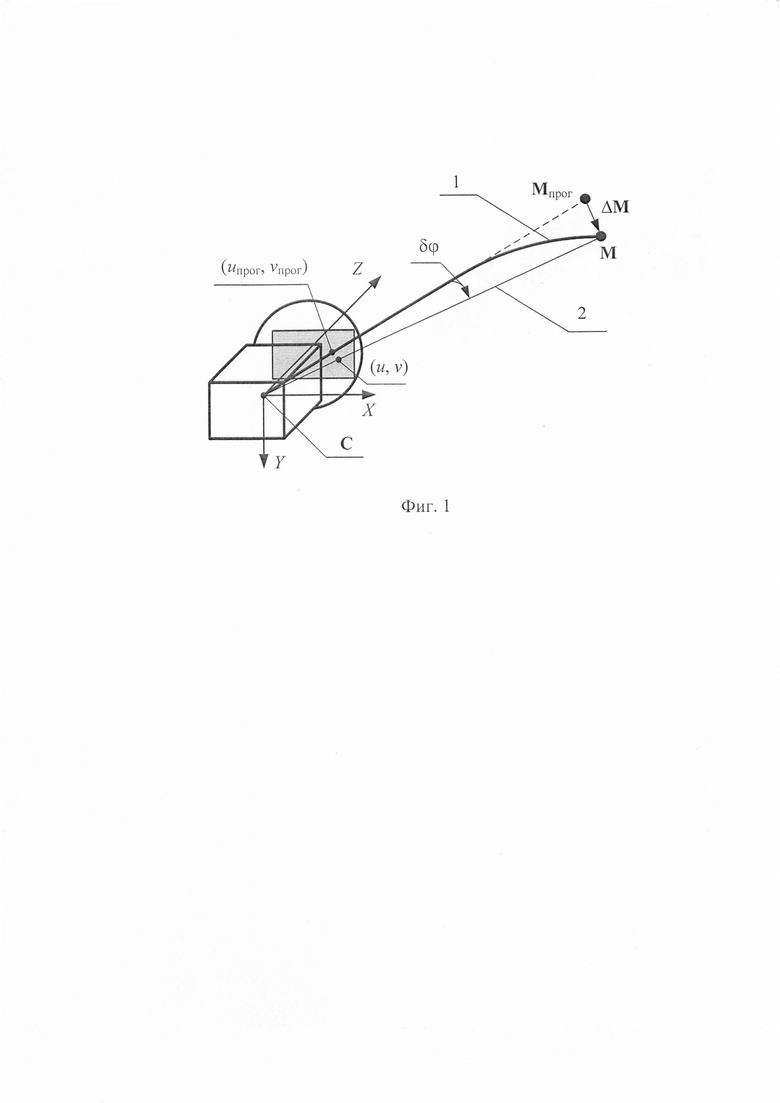
Принятие перечисленных ограничений позволяет отказаться от процедуры перебора при уточнении пространственных координат репера на анализируемом деформируемом объекте 1 и выполнить поиск непосредственно на линии 2 с направляющим вектором v. При этом линия 2 соединяет оптический центр камеры С (см. фиг. 1) с центром проекции репера на плоскости изображения (u, v):

Вектор, соответствующий прогнозируемому положению отметки от репера, вычисленному на основании параметров математической модели проективной камеры и прогнозируемых пространственных координат репера в системе координат камеры Мпрог=[Хпрог, Yпрог, Zпрог], равен
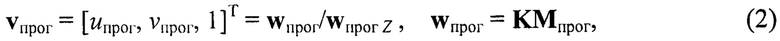
где wпрог Z - последний (третий) элемент вектора wпрог.
Угол между векторами vпрог и v:
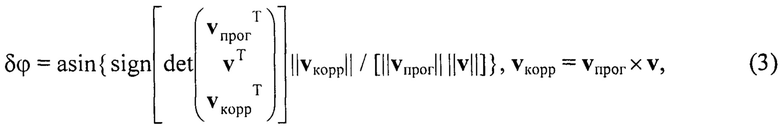
где «×» - символ векторного умножения векторов, ||⋅|| - два-норма вектора, det(⋅) - операция вычисления определителя матрицы, sign[⋅] - функция знака.
Принимая гипотезу о том, что величина деформации жесткого объекта много меньше Zпрог, получим, что δϕ≈0 и, следовательно, справедливо (см. фиг. 1) равенство
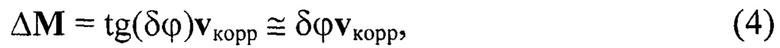
поэтому уточненное положение пространственных координат репера

Таким образом, для уточнения пространственных координат каждой реперной точки необходимо:
- оценить двумерные координаты центра отметки репера в плоскости изображения регистрирующей камеры (u, v);
- вычислить направляющий вектор v на центр репера в системе координат регистрирующей камеры по (1);
- оценить пиксельные координаты для прогнозируемой отметки от реперной точки и соответствующий ей направляющий вектор vпрог по (2);
- вычислить, используя векторное произведение векторов, угол δϕ между векторами vпрог и v с учетом его знака по (3);
- сформировать вектор поправки пространственных координат ΔМ по (4),
- выполнить коррекцию прогнозируемых пространственных координат реперной отметки по (5).
Если же, как в способе прототипа, задача измерений пространственных координат точек объекта реализуется не в системе координат камеры, а в иной рабочей системе координат, то перед применением формулы (2) требуется предварительно выполнить пересчет пространственных координат репера Мраб из рабочей системы координат в систему координат камеры через матрицу трансформации:
Мпрог=[R|t]⋅[Мпрог_рабТ|1]Т,
а скорректированным положением репера в рабочей системе координат считать значение
Мраб=[R|t]-1⋅[МТ|1]Т,
где «А | В» - обозначение операции аугментации, т.е. пристыковки массива В к массиву А справа, a R и t - соответственно матрица поворота и вектор параллельного переноса для перехода из рабочей системы координат в систему координат камеры.
Изобретение относится к области оптических измерений трехмерных координат объектов в пространстве, в частности к фото- и видеограмметрии. Способ измерения пространственных координат точек объекта с высокой продольной жесткостью заключается в том, что на поверхности объекта располагают реперы. При этом на участках ожидаемой минимальной деформации выделяют группу базовых реперов. Далее определяют начальные трехмерные координаты реперов, при нагружении объекта фиксируют его изображение, на котором определяют двумерные координаты образов всех реперов, находят искомые трехмерные координаты всех реперов, при этом последовательно определяют прогнозируемые значения трехмерных координат реперов, используя заданные геометрические связи и исходные трехмерные координаты базовых реперов и/или найденные трехмерные координаты реперов, следующих за базовыми реперами, определяют прогнозируемые значения трехмерных координат каждого репера. Затем производят уточнение трехмерных координат и принимают за результирующие координаты текущего репера результат уточнения, при этом вычисляют направляющий вектор v на центр репера в системе координат регистрирующей камеры, оценивают пиксельные координаты для прогнозируемой отметки от реперной точки и соответствующий ей направляющий вектор vпрог, вычисляют угол δϕ между векторами vпрог и v с учетом его знака, формируют с учетом данного угла вектор поправки пространственных координат ΔM и выполняют уточнение прогнозируемой пространственной координаты репера по формуле М=Мпрог+ΔМ. Технический результат заключается в разработке однократно выполняемой в каждом цикле измерения пространственных координат процедуры уточнения прогнозируемых трехмерных координат точки, не содержащей перебора всех ее возможных положений внутри пространственного элемента объема. 1 ил.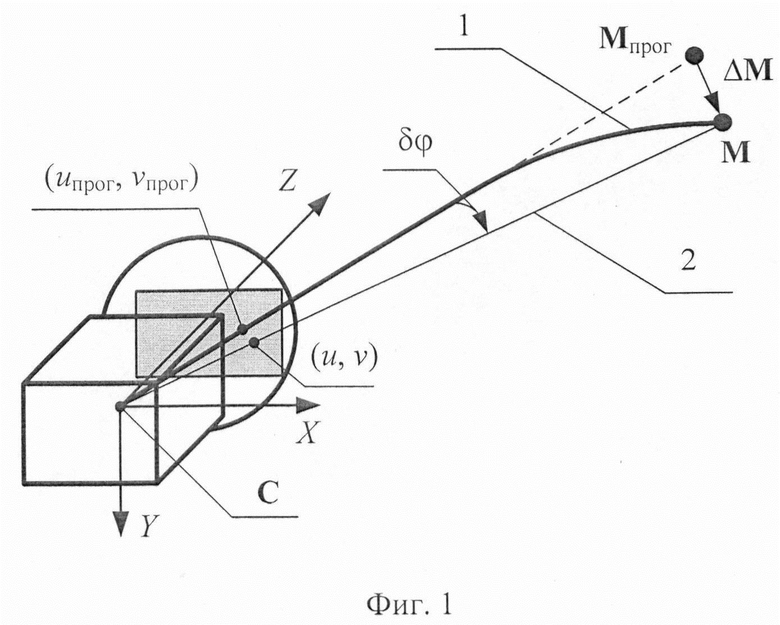
Способ измерения пространственных координат точек объекта с высокой продольной жесткостью, в котором на поверхности объекта располагают реперы, при этом реперы размещают в соответствии с заданными исходными геометрическими связями между ними, на участках ожидаемой минимальной деформации выделяют группу базовых реперов и определяют их начальные трехмерные координаты, при нагружении объекта фиксируют его изображение, на котором определяют двумерные координаты образов всех реперов, находят искомые трехмерные координаты всех реперов, при этом последовательно определяют прогнозируемые значения трехмерных координат реперов, используя заданные геометрические связи и исходные трехмерные координаты базовых реперов и/или найденные трехмерные координаты реперов, следующих за базовыми реперами, определяют прогнозируемые значения трехмерных координат каждого репера, производят уточнение трехмерных координат и принимают за результирующие координаты текущего репера результат уточнения, отличающийся тем, что вычисляют направляющий вектор v на центр репера в системе координат регистрирующей камеры, оценивают пиксельные координаты для прогнозируемой отметки от реперной точки и соответствующий ей направляющий вектор vпрог, вычисляют угол δϕ между векторами vпрог и v с учетом его знака, формируют с учетом данного угла вектор поправки пространственных координат ΔM и выполняют уточнение прогнозируемой пространственной координаты репера по формуле М=Мпрог+ΔМ.
| ТЕНЗОМЕТРИЧЕСКИЙ ДАТЧИК И СИСТЕМА ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННОГО ПОЛОЖЕНИЯ ТАКИХ ДАТЧИКОВ | 2010 |
|
RU2596064C2 |
| СИСТЕМА КОНТРОЛЯ ЛЕТАТЕЛЬНОГО АППАРАТА | 2017 |
|
RU2737766C2 |
| Способ саморегулирования концентрации компонентов электролита | 1989 |
|
SU1696606A1 |
| US 20050008256 A1, 13.01.2005 | |||
| US 9816809 B2, 14.11.2017 | |||
| Кудинов И.А., Павлов О.В., Холопов И.С | |||
| Реализация алгоритма определения пространственных координат и угловой ориентации объекта по реперным точкам, использующего информацию от одной камеры // Компьютерная | |||
Авторы
Даты
2025-02-24—Публикация
2024-03-14—Подача