Изобретение относится к области точного приборостроения и может быть использовано при создании систем начальной ориентации различных объектов на основе использования спутниковых измерений. Известны способы определения начальной ориентации на основе спутниковых измерений, использующие для определения углов ориентации объекта относительно выбранной системы координат (географической или геоцентрической) фазовые измерения спутниковой группировки [Г.И. Емельянцев, А.П. Степанов, Б.А. Блажное, И.В. Семенов. О повышении точности GPS-компаса для малоразмерных объектов // Гироскопия и навигация. 2015. №1. С. 18-28; Э.М. Шохин. Математический анализ фазовых погрешностей в схеме слежения приемника GPS при помехах разного рода // Гироскопия и навигация. 2018. №3. С. 40-53; И.О. Митрахович. Система определения углов ориентации объектов в пространстве на основе метода RTK // Интеллектуальные и сенсорные системы - 2016: Сборник научных трудов по материалам Республиканской научно-технической конференции [Электронный ресурс] / Минск: БИТУ, 2016; В.И. Тяпкин, Е.Н. Гарин. Методы определения навигационных параметров подвижных средств с использованием спутниковой радионавигационной системы ГЛОНАСС / Красноярск: Сиб. федер. ун-т, 2012. 260 с.; Г.И. Емелъянцев, А.П. Степанов, Б.А. Блажное. О начальной выставке и оценке погрешностей измерительного модуля БИНС с использованием спутниковых фазовых измерений // Гироскопия и навигация. 2019. №1. С. 47-60]. Недостатками их являются сложность решения проблемы неоднозначности фазовых определений, связанные с ней существенные вычислительные затраты и критичное влияние шумов фазовых определений на общую точность оценки углов начальной ориентации. Наиболее близким к предлагаемому изобретению является способ, состоящий в вычислении разностей фазовых измерений с последующим их комплексированием с измерениями ИНС и обработкой общего вектора измерений в фильтре Калмана для определения искомых параметров ориентации [D.Kaleev, A. Pereverzev, Yu. Savchenko, A .Silantiev. Error estimation and selection of inertial navigation system parameters for uncoupled integration with multi-antenna systems // 2016 IEEE NW Russia Young Researchers in Electrical and Electronic Engineering Conference (EIConRusNW). P. 414-417]. Недостатками данного способа являются существенные вычислительные затраты, обусловленные двухэтапной процедурой обработки спутниковых измерений, аппаратурные затраты в силу необходимости использования ИНС и низкая точность, обусловленная погрешностями чувствительных элементов ИНС (для которой, в свою очередь, необходима своя начальная выставка).
Заявленное изобретение направлено на решение задач снижения вычислительных и аппаратурных затрат и повышения точности определения начальной ориентации объектов.
Поставленная задача возникает при разработке навигационных систем и систем начальной ориентации различных объектов.
Для обеспечения высокой точности определения начальной ориентации объекта предлагается способ, заключающийся в том, что по показаниям размещенных на жестком основании двух спутниковых навигационных приемников (СИП), симметрично расположенных относительно центра масс объекта на известном расстоянии от него вдоль оси крена, в режиме высокоточного позиционирования определяются координаты обоих СИП в геоцентрической системе координат, по значениям которых определяются координаты центра масс объекта как середины вектора, лежащего между точками расположения СИП, после чего определяется косинус первого угла, образованного в геоцентрической системе координат векторами, лежащими между точкой расположения первого СИП и центром масс объекта и между началом геоцентрической системы координат и центром масс объекта, а также косинус второго угла, образованного векторами, лежащими между точкой расположения второго СНП и центром масс объекта и между началом геоцентрической системы координат и центром масс объекта, по значениям которых, определяемых как отношения разностей скалярного произведения векторов, определяющих положение соответствующего СНП в геоцентрической системе координат и центра масс объекта, и квадрата расстояния центра масс объекта от начала геоцентрической системы координат к произведению расстояния между соответствующим СНП и центром масс объекта на расстояние центра масс объекта от начала геоцентрической системы координат, определяется точный угол тангажа как арксинус половины разности косинусов второго и первого углов, после чего определяется первый косинус угла азимута как угла, образованного в геоцентрической системе координат проекцией вектора, лежащего между точками расположения первого СНП и центра масс объекта, на плоскость горизонта и вектора, лежащего в плоскости горизонта между центром масс объекта и точкой пересечения меридиональной оси географической системы координат с осью вращения Земли, а также второй косинус угла азимута как угла, образованного в геоцентрической системе координат проекцией вектора, лежащего между точками расположения второго СНП и центра масс объекта, на плоскость горизонта и вектора, лежащего в плоскости горизонта между центром масс объекта и точкой пересечения меридиональной оси географической системы координат с осью вращения Земли, определяемые как отношения разностей произведения квадрата расстояния центра масс объекта от начала геоцентрической системы координат на отношение проекций векторов, определяющих положение соответствующего СНП и центра масс объекта в геоцентрической системе координат, на ее ось, совпадающую с осью вращения Земли, и скалярного произведения векторов, определяющих положение соответствующего СНП и центра масс объекта в геоцентрической системе координат, к произведению расстояния между СНП и центром масс объекта на расстояние центра масс объекта от начала геоцентрической системы координат и на косинус угла тангажа, а также на корень квадратный разности с единицей отношения квадрата расстояния центра масс объекта от начала геоцентрической системы координат к квадрату проекции вектора, определяющего положение центра масс объекта в геоцентрической системе координат, на ее ось, совпадающую с осью вращения Земли, после чего определяется точный угол азимута как арккосинус половины разности первого и второго косинусов угла азимута, после чего основание с размещенными на нем СНП выставляется в направлении оси тангажа и по показаниям обоих СНП определяются их новые координаты, после чего определяется косинус первого угла, образованного в геоцентрической системе координат векторами, лежащими между точкой нового расположения первого СНП и центром масс объекта и между началом геоцентрической системы координат и центром масс объекта, а также косинус второго угла, образованного векторами, лежащими между точкой нового расположения второго СНП и центром масс объекта и между началом геоцентрической системы координат и центром масс объекта, по значениям которых, определяемых как отношения разностей скалярного произведения векторов, определяющих новое положение соответствующего СНП в геоцентрической системе координат и центра масс объекта, и квадрата расстояния центра масс объекта от начала геоцентрической системы координат к произведению расстояния между соответствующим СНП и центром масс объекта на расстояние центра масс объекта от начала геоцентрической системы координат, определяется точный угол крена как арксинус половины разности косинусов второго и первого углов.
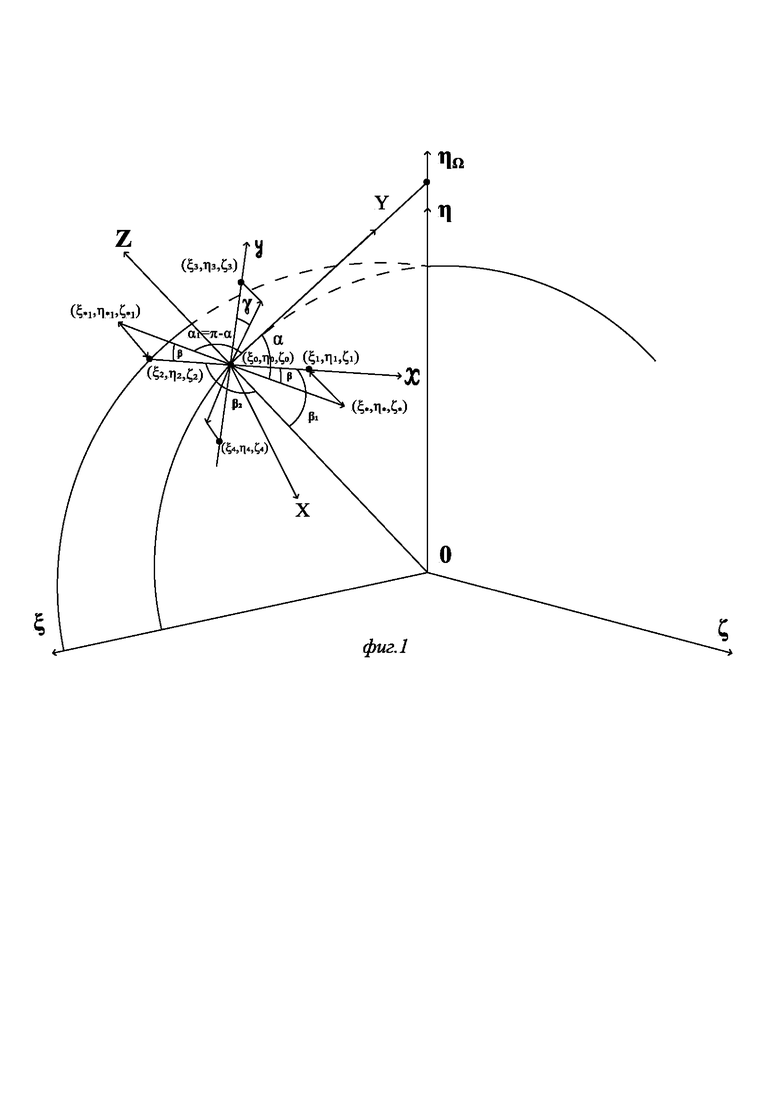
Для описания существа способа определения начальной ориентации используем следующие системы координат (СК) (фиг. 1):
- геоцентрическую СК (ГцСК) 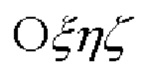 с началом в центре Земли, ось
с началом в центре Земли, ось 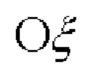 которой лежит в плоскости нулевого меридиана, ось
которой лежит в плоскости нулевого меридиана, ось 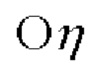 совпадает с осью вращения Земли, а ось
совпадает с осью вращения Земли, а ось 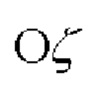 дополняет систему координат до правой,
дополняет систему координат до правой,
- географическую СК (ГСК) OXYZ с началом в центре масс (ЦМ) объекта, ось OY которой лежит в плоскости местного меридиана и направлена на Север (меридиональная ось), ось OZ направлена от центра Земли, а ось ОХ дополняет систему координат до правой,
- приборную СК (ПСК) 0xyz с началом в ЦМ объекта, оси которой при отсутствии углов разворота относительно ГСК совпадают с соответствующими (одноименными) осями ГСК.
В данном способе углы начальной ориентации ПСК, связанной с объектом, определяются по показаниям размещенных на жестком основании двух спутниковых навигационных приемников (СНП), симметрично расположенных относительно ЦМ объекта на известном расстоянии L от него вдоль оси Ох (оси крена) ПСК.
СНП работают в режиме высокоточного позиционирования (в частности, RTK, например, сетевом или инверсном), обеспечивая, тем самым, сантиметровую (при долговременном позиционировании - миллиметровую) точность определения их координат в ГцСК: 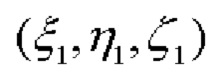 - координаты первого СНП,
- координаты первого СНП, 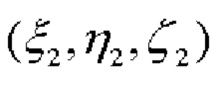 - координаты второго (фиг. 1). Полученные по спутниковым измерениям координаты обоих СНП позволяют определить углы азимута α и наклона относительно плоскости горизонта - тангажа β и крена γ, следующим образом.
- координаты второго (фиг. 1). Полученные по спутниковым измерениям координаты обоих СНП позволяют определить углы азимута α и наклона относительно плоскости горизонта - тангажа β и крена γ, следующим образом.
Сначала по показаниям обоих СНП определяются координаты ЦМ объекта как середины вектора, лежащего между точками расположения СНП:
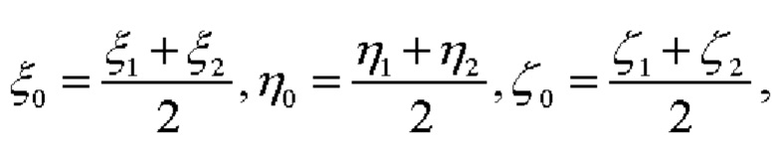
после чего определяется косинус угла β1, образованного векторами  (фиг. 1):
(фиг. 1):
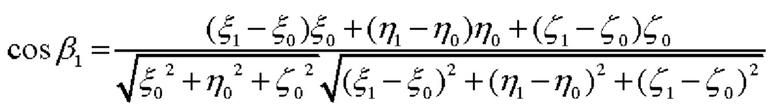
и косинус угла β2, образованного векторами 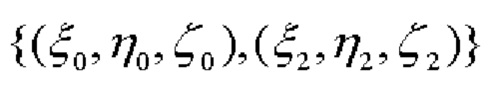 и
и 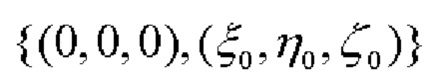 (фиг. 1):
(фиг. 1):
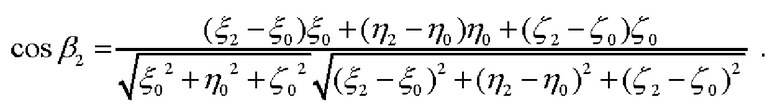
Если ЦМ объекта расположен непосредственно на сфере Земли, то с учетом очевидного соотношения 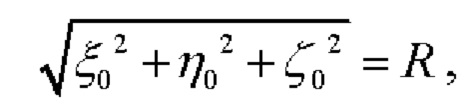 а также того обстоятельства, что значение
а также того обстоятельства, что значение 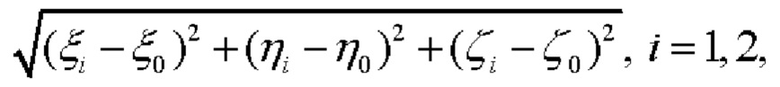 равно известному и неизменному (по условию) расстоянию L между СНП и ЦМ объекта, определение косинусов обоих углов
равно известному и неизменному (по условию) расстоянию L между СНП и ЦМ объекта, определение косинусов обоих углов 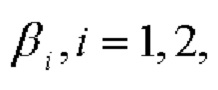 упрощается:
упрощается:
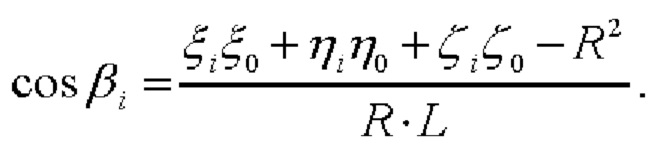
Т.к., несмотря на высокую точность позиционирования, координаты СНП определяются, тем не менее, с некоторой погрешностью (причем, в силу близкого расположения СНП, практически одинаковой для обоих СНП), то результат вычисления косинусов углов βi может быть записан как
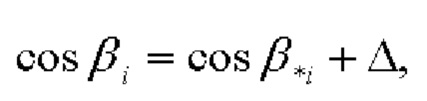
где 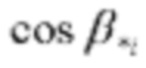 - точное значение косинуса угла βi,
- точное значение косинуса угла βi,
Δ - ошибка оценки косинуса угла βi.
С учетом того, что 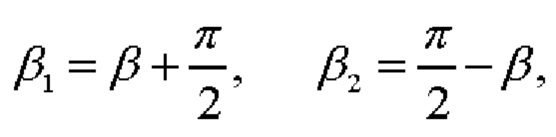 где β - угол тангажа, результат вычисления косинусов углов βi может быть представлен следующим образом:
где β - угол тангажа, результат вычисления косинусов углов βi может быть представлен следующим образом:
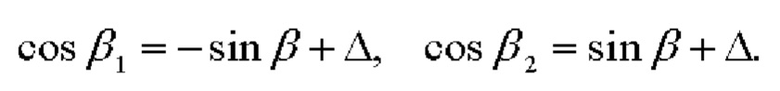
Разность вычисленных значений косинусов углов βi позволяет определить с высокой точностью угол тангажа β как:
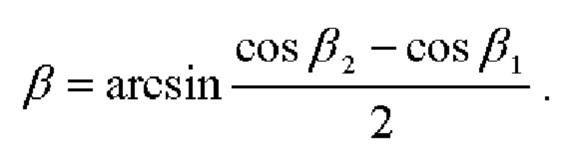
После высокоточного определения угла тангажа β определяется косинус угла азимута α как угла, образованного проекцией 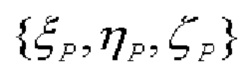 вектора
вектора 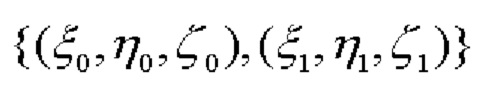 на плоскость горизонта и вектором
на плоскость горизонта и вектором 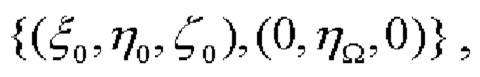 совпадающего по направлению с меридиональной осью OY ГСК и имеющего в качестве координат его начальной и конечной точек, соответственно, координаты ЦМ объекта и точки пересечения оси OY ГСК с осью вращения Земли (фиг. 1). Исходя из фиг. 1 и используя простейшие тригонометрические соотношения, можно показать, что координата ηΩ в данном случае определяется как:
совпадающего по направлению с меридиональной осью OY ГСК и имеющего в качестве координат его начальной и конечной точек, соответственно, координаты ЦМ объекта и точки пересечения оси OY ГСК с осью вращения Земли (фиг. 1). Исходя из фиг. 1 и используя простейшие тригонометрические соотношения, можно показать, что координата ηΩ в данном случае определяется как:
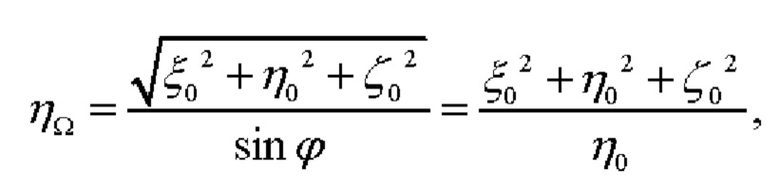
а если ЦМ объекта расположен на сфере Земли, то
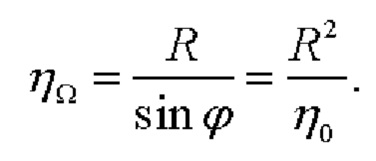
Т.к. координаты  точки проекции точки
точки проекции точки  на плоскость OXJ равны (с учетом коллинеарности векторов
на плоскость OXJ равны (с учетом коллинеарности векторов 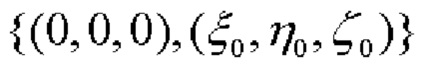 и
и 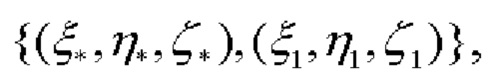 модуль которого равен
модуль которого равен 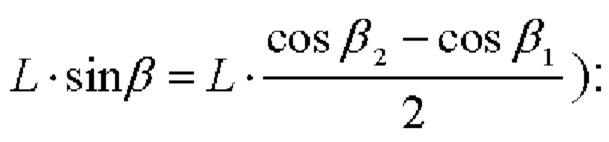
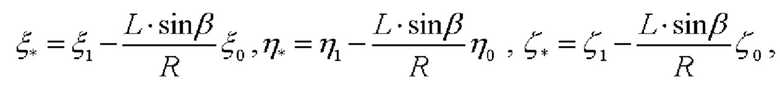
то вектор-проекция 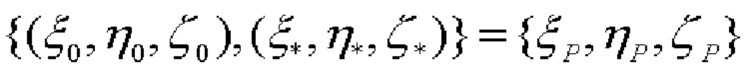 (модуль которого равен Lcosβ), соответственно, определяется как:
(модуль которого равен Lcosβ), соответственно, определяется как:
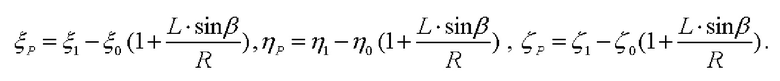
В соответствии с приведенными выше определениями угла азимута α и вектора-проекции 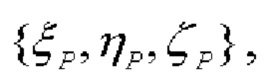 косинус угла азимута αравен (для упрощения записи используем случай размещения ЦМ объекта на сфере Земли):
косинус угла азимута αравен (для упрощения записи используем случай размещения ЦМ объекта на сфере Земли):

Одновременно определяется косинус угла α1, образованного проекцией 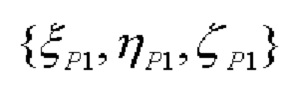 вектора
вектора 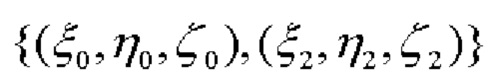 на плоскость горизонта и рассмотренного выше вектора
на плоскость горизонта и рассмотренного выше вектора 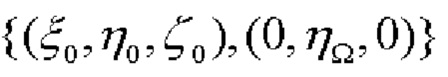 (фиг. 1).
(фиг. 1).
С учетом коллинеарности векторов 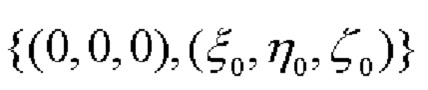 и
и 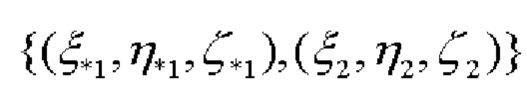 (модуль которого равен L⋅sinβ), координаты
(модуль которого равен L⋅sinβ), координаты 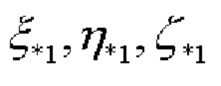 точки проекции точки
точки проекции точки 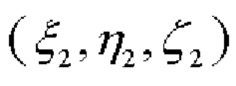 на плоскость OXY равны:
на плоскость OXY равны:
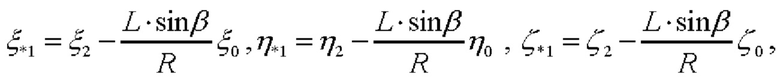
а вектор-проекция 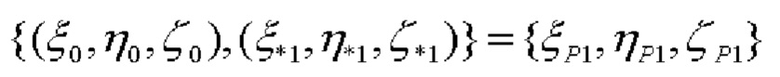 (модуль которого равен Lcosβ), соответственно, определяется как:
(модуль которого равен Lcosβ), соответственно, определяется как:
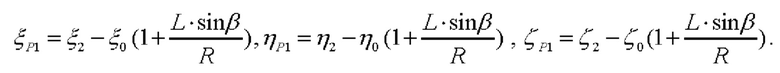
В соответствии с приведенными выше определениями, косинус угла α1 равен:
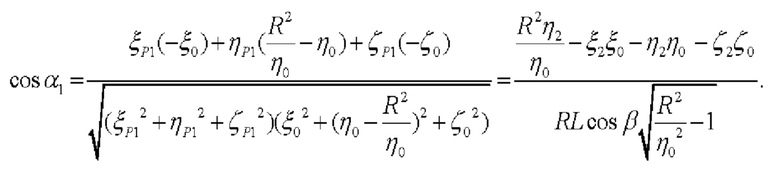
С учетом соображений о погрешностях определения косинусов углов по показаниям СНП, изложенных выше, результат вычисления косинусов углов α1 и α2 может быть записан как:
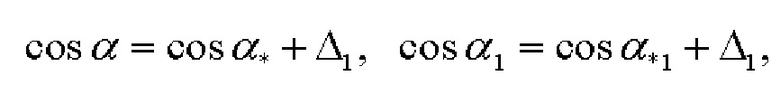
где 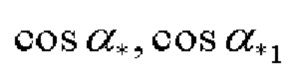 - точные значения косинусов углов
- точные значения косинусов углов 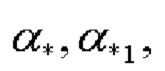
Δ1 - ошибка оценки косинусов углов 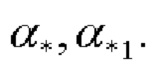
С учетом того, что 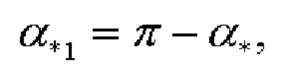 где
где 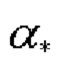 - точное значение угла азимута, результат вычисления косинуса угла
- точное значение угла азимута, результат вычисления косинуса угла 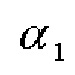 может быть представлен следующим образом:
может быть представлен следующим образом:
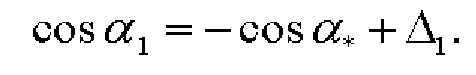
Разность вычисленных значений косинусов углов 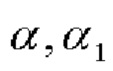 позволяет определить с высокой точностью угол азимута
позволяет определить с высокой точностью угол азимута 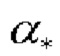 как:
как:
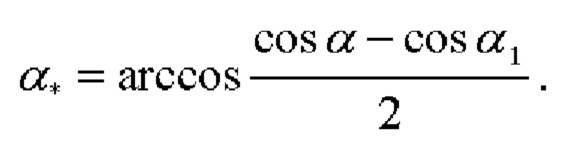
После высокоточного определения углов азимута α* и тангажа β основание, на котором размещены СНП, разворачиваясь относительно ЦМ объекта, выставляется в направлении оси Оу (оси тангажа) ПСК. Далее по показаниям СНП определяются их новые координаты  после чего аналогично определению угла тангажа определяется угол крена γ:
после чего аналогично определению угла тангажа определяется угол крена γ:
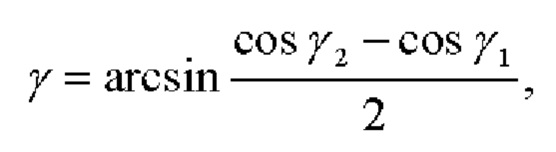
где γ1 - угол, образованный векторами  и
и 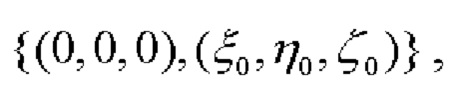
γ2 - угол, образованный векторами 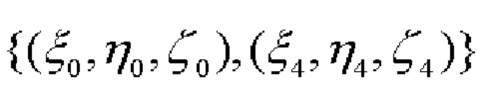 и
и 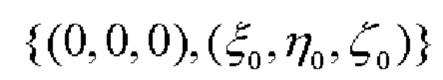 (фиг. 1),
(фиг. 1),
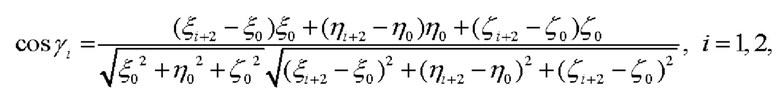
а если ЦМ объекта расположен непосредственно на сфере Земли, то:
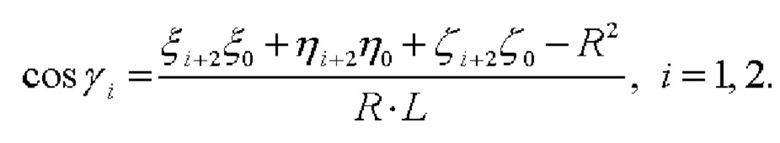
Таким образом, предложенный способ состоит в том, что на первом шаге по показаниям размещенных на жестком основании двух СНП, симметрично расположенных относительно ЦМ объекта на известном расстоянии L от него в направлении оси крена, в режиме высокоточного позиционирования (например, RTK) определяются их координаты в ГцСК: 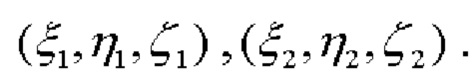 На втором шаге определяются координаты ЦМ объекта как середины вектора, лежащего между точками расположения СНП. На третьем шаге определяется косинус первого угла, образованного в ГцСК векторами, лежащими между точкой расположения первого СНП и ЦМ объекта и между началом ГцСК и ЦМ объекта, а также косинус второго угла, образованного векторами, лежащими между точкой расположения второго СНП и ЦМ объекта и между началом ГцСК и ЦМ объекта. На четвертом шаге определяется точный угол тангажа как арксинус половины разности косинусов второго и первого угла.
На втором шаге определяются координаты ЦМ объекта как середины вектора, лежащего между точками расположения СНП. На третьем шаге определяется косинус первого угла, образованного в ГцСК векторами, лежащими между точкой расположения первого СНП и ЦМ объекта и между началом ГцСК и ЦМ объекта, а также косинус второго угла, образованного векторами, лежащими между точкой расположения второго СНП и ЦМ объекта и между началом ГцСК и ЦМ объекта. На четвертом шаге определяется точный угол тангажа как арксинус половины разности косинусов второго и первого угла.
На пятом шаге определяется первый косинус угла азимута как угла, образованного в ГцСК проекцией вектора, лежащего между точками расположения первого СНП и ЦМ объекта, на плоскость горизонта и вектора, лежащего в плоскости горизонта между ЦМ объекта и точкой пересечения меридиональной оси OY ГСК с осью вращения Земли, а также второй косинус угла азимута как угла, образованного в ГцСК проекцией вектора, лежащего между точками расположения второго СНП и ЦМ объекта, на плоскость горизонта и вектора, лежащего в плоскости горизонта между ЦМ объекта и точкой пересечения оси OY ГСК с осью вращения Земли. На шестом шаге определяется точный угол азимута как арккосинус половины разности первого и второго косинусов угла азимута.
На седьмом шаге основание с размещенными на нем СНП, разворачиваясь относительно ЦМ объекта, выставляется в направлении оси тангажа, после чего по показаниям обоих СНП определяются их новые координаты.
На восьмом шаге определяется косинус первого угла, образованного в ГцСК векторами, лежащими между точкой нового расположения первого СНП и ЦМ объекта и между началом ГцСК и ЦМ объекта, а также косинус второго угла, образованного векторами, лежащими между точкой нового расположения второго СНП и ЦМ объекта и между началом ГцСК и ЦМ объекта. На девятом шаге определяется точный угол крена как арксинус половины разности косинусов второго и первого угла.
Проведенные вычисления при погрешностях 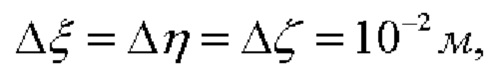 обеспечиваемых СНП в режиме RTK, показали, что при разнесении СНП на L=1 м ошибки определения данных функций не превышают 4⋅10-2, а при L=10 м, соответственно, 4⋅10-3, причем, для всего диапазона углов. При долговременном позиционировании, когда погрешности определения координат равны уже
обеспечиваемых СНП в режиме RTK, показали, что при разнесении СНП на L=1 м ошибки определения данных функций не превышают 4⋅10-2, а при L=10 м, соответственно, 4⋅10-3, причем, для всего диапазона углов. При долговременном позиционировании, когда погрешности определения координат равны уже 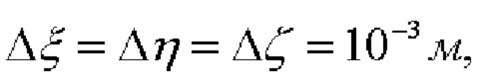 ошибки вычисления данных функций уменьшаются на порядок и не превышают 4⋅10-3 при L=1 м, и 4⋅10-4, соответственно, при L=10 м. При использовании предложенного способа ошибки определения данных функций становятся соизмеримыми с ошибками их компьютерного вычисления, что позволяет использовать предложенный способ для определения начальной ориентации с требуемой для соответствующих объектов точностью (определяемой габаритами объекта и допустимым временем позиционирования) с минимальными на сегодняшний день вычислительными и аппаратурными затратами.
ошибки вычисления данных функций уменьшаются на порядок и не превышают 4⋅10-3 при L=1 м, и 4⋅10-4, соответственно, при L=10 м. При использовании предложенного способа ошибки определения данных функций становятся соизмеримыми с ошибками их компьютерного вычисления, что позволяет использовать предложенный способ для определения начальной ориентации с требуемой для соответствующих объектов точностью (определяемой габаритами объекта и допустимым временем позиционирования) с минимальными на сегодняшний день вычислительными и аппаратурными затратами.
Изобретение относится к области точного приборостроения и может быть использовано при создании систем начальной ориентации различных объектов на основе использования спутниковых измерений. Способ определения начальной ориентации объекта состоит в том, что по показаниям размещенных на жестком основании двух спутниковых навигационных приемников (СНП), симметрично расположенных относительно центра масс объекта на известном расстоянии от него вдоль оси крена, в режиме высокоточного позиционирования определяются координаты обоих СНП в геоцентрической системе координат. По этим значениям определяются координаты центра масс объекта как середины вектора, лежащего между точками расположения СНП, после чего определяется косинус первого угла, образованного в геоцентрической системе координат векторами, лежащими между точкой расположения первого СНП и центром масс объекта и между началом геоцентрической системы координат и центром масс объекта, а также косинус второго угла, образованного векторами, лежащими между точкой расположения второго СНП и центром масс объекта и между началом геоцентрической системы координат и центром масс объекта, по значениям которых определяется угол тангажа. После чего определяется угол азимута, после чего основание с размещенными на нем СНП выставляется в направлении оси тангажа и по показаниям обоих СНП определяются их новые координаты. Далее определяется косинус первого угла, образованного в геоцентрической системе координат векторами, лежащими между точкой нового расположения первого СНП и центром масс объекта и между началом геоцентрической системы координат и центром масс объекта, аналогично определяется косинус второго угла, учитывая новое расположение второго СНП, по значениям которых определяется угол крена. Технический результат – повышение точности определения начальной ориентации объектов. 1 ил.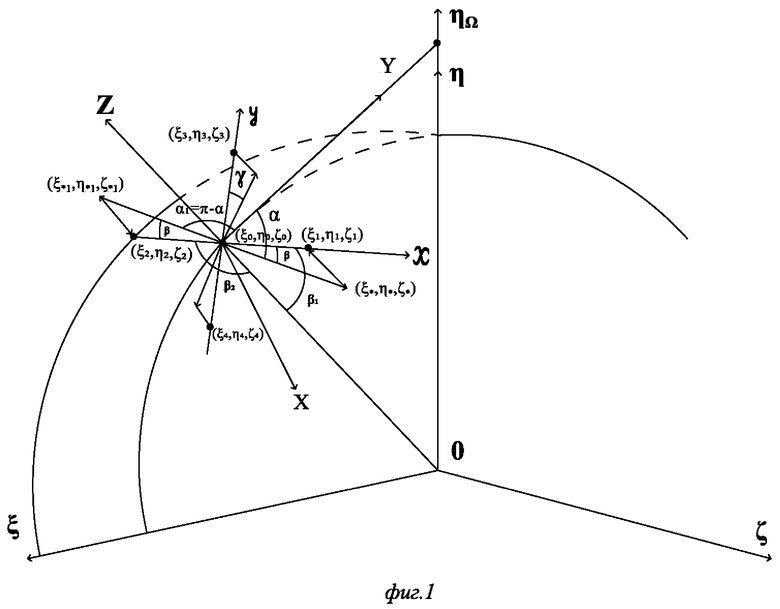
Способ определения начальной ориентации объекта, заключающийся в том, что по показаниям размещенных на жестком основании двух спутниковых навигационных приемников (СНП), симметрично расположенных относительно центра масс объекта на известном расстоянии от него вдоль оси крена, в режиме высокоточного позиционирования определяются координаты обоих СНП в геоцентрической системе координат, по значениям которых определяются координаты центра масс объекта как середины вектора, лежащего между точками расположения СНП, после чего определяется косинус первого угла, образованного в геоцентрической системе координат векторами, лежащими между точкой расположения первого СНП и центром масс объекта и между началом геоцентрической системы координат и центром масс объекта, а также косинус второго угла, образованного векторами, лежащими между точкой расположения второго СНП и центром масс объекта и между началом геоцентрической системы координат и центром масс объекта, по значениям которых, определяемым как отношения разностей скалярного произведения векторов, определяющих положение соответствующего СНП в геоцентрической системе координат и центра масс объекта, и квадрата расстояния центра масс объекта от начала геоцентрической системы координат к произведению расстояния между соответствующим СНП и центром масс объекта на расстояние центра масс объекта от начала геоцентрической системы координат, определяется точный угол тангажа как арксинус половины разности косинусов второго и первого углов, после чего определяется первый косинус угла азимута как угла, образованного в геоцентрической системе координат проекцией вектора, лежащего между точками расположения первого СНП и центра масс объекта, на плоскость горизонта и вектора, лежащего в плоскости горизонта между центром масс объекта и точкой пересечения меридиональной оси географической системы координат с осью вращения Земли, а также второй косинус угла азимута как угла, образованного в геоцентрической системе координат проекцией вектора, лежащего между точками расположения второго СНП и центра масс объекта, на плоскость горизонта и вектора, лежащего в плоскости горизонта между центром масс объекта и точкой пересечения меридиональной оси географической системы координат с осью вращения Земли, определяемые как отношения разностей произведения квадрата расстояния центра масс объекта от начала геоцентрической системы координат на отношение проекций векторов, определяющих положение соответствующего СНП и центра масс объекта в геоцентрической системе координат, на ее ось, совпадающую с осью вращения Земли, и скалярного произведения векторов, определяющих положение соответствующего СНП и центра масс объекта в геоцентрической системе координат, к произведению расстояния между СНП и центром масс объекта на расстояние центра масс объекта от начала геоцентрической системы координат и на косинус угла тангажа, а также на корень квадратный разности с единицей отношения квадрата расстояния центра масс объекта от начала геоцентрической системы координат к квадрату проекции вектора, определяющего положение центра масс объекта в геоцентрической системе координат, на ее ось, совпадающую с осью вращения Земли, после чего определяется точный угол азимута как арккосинус половины разности первого и второго косинусов угла азимута, после чего основание с размещенными на нем СНП выставляется в направлении оси тангажа и по показаниям обоих СНП определяются их новые координаты, после чего определяется косинус первого угла, образованного в геоцентрической системе координат векторами, лежащими между точкой нового расположения первого СНП и центром масс объекта и между началом геоцентрической системы координат и центром масс объекта, а также косинус второго угла, образованного векторами, лежащими между точкой нового расположения второго СНП и центром масс объекта и между началом геоцентрической системы координат и центром масс объекта, по значениям которых, определяемым как отношения разностей скалярного произведения векторов, определяющих новое положение соответствующего СНП в геоцентрической системе координат и центра масс объекта, и квадрата расстояния центра масс объекта от начала геоцентрической системы координат к произведению расстояния между соответствующим СНП и центром масс объекта на расстояние центра масс объекта от начала геоцентрической системы координат, определяется точный угол крена как арксинус половины разности косинусов второго и первого углов.
| СПОСОБ ОПРЕДЕЛЕНИЯ НАЧАЛЬНОЙ ОРИЕНТАЦИИ ОБЪЕКТА | 2020 |
|
RU2754087C1 |
| Способ ориентации космического аппарата | 2020 |
|
RU2735120C1 |
| Способ высокоточного определения навигационных элементов движения судна | 2016 |
|
RU2643072C2 |
| Колосоуборка | 1923 |
|
SU2009A1 |
Авторы
Даты
2025-03-11—Публикация
2024-03-13—Подача