N3
О
С71
оо
Изобретение относится к мгиииностроению н может быть использовано в передаточных механизмах.
Целью изобретения является повышение несущей способности и долговечности передачи за счет равномерного изменения направления линии действия реакции в выс1ней паре.
На чертеже изображена схема заценления зубьев зубчатых колес друг с другом и заценле1 ие каждого колеса с производящим исходным контуром.
Зубчатая передача содержит зубчатые колеса 1 и 2, схема зацепления зубьев которых друг с другом и зацепление каждого колеса с производящим исходным контуром 3 изображена на чертеже. Профили зубьев колес образуются нри их взаимодействии с зубьями производящего исходного контура 3. Начальные окружности колес совпадают с делительными и обозначены щтрихпунктирными линиями. В нолюсе П заценления происходит касание начальных окружностей. В рассматриваемом положении с iiojnocoM И совпадает начало координат, жестко связанных с нроизводящим исходным контуром. Ось Их совпадает с делительной прямой гфоизводя1пего исходного контура, а ось Иу ей нернендикулярна. На главном профиле производяntero исходного контура показапа точка А с координатами х и у. На линии Р|Р-) зацепления ей соответствует точка АО. Отрезок ИАо расположен на нормали к сопряженным Г1рофилям в момент из касания з точке АО и образует с прямой линией, перпендикулярной к линии межосевого расстояния, совнадаюнгей с осью Иу угол а. Величина угла а дости1ает максимума при контакте зубьев колес в нолюсе И и изменяется но линейному закону в функции углов поворота колес. Величина угла а при касании зубьев в нолюсе И принята равной 45°, так как в этом случае величина контактных напряжений будет минимальной. Угол 11рофи;1Я зуба нроизводящего контура в точке, расположенной на делительной прямой и совнадаюнгей в данный момент с нолюсом И, также равен 45°. Угол профиля производяпдего исходного контура для точки, расположенной на прямой, линии, параллельной делительной прямой и отстоящей от нее на расстоянии ha, равен eta. Тогда углы нак.лона касательных, проведенных через уномянутые точки, к оси Их соответственно составят - - и - оса. Если величина угла наклона касательной к профилю зуба производянхего исходно о контура будет из.меняться по линейному закону, то величина угла а также будет изменяться по линейному закону в функции углов поворота колес или то же самое в функции пере.мещения исходного производящего контура. Учитывая, что величина тангенса угла наклона касательной к профилю зуба производящего исход|1ого кон
тура, описываемому уравнением (х), равна значению производной в этой точке, имеем
IFJf
,
X
где ха- координата точки профиля производящего исходного контура, расположенного на прямой линии, параллельной делительной прямой и отстоящей от нее на расстоянии ha, 15равном высоте головки зуба.
Интегрируя уравнение (1), получим
y Stg )dx
Ха
Г
20 -4 (-
0|+С(2)
Ха
Иредлагаем и , тогда величина произвольной постоянной определится как
С - -Inlcosf I,(3)
-fаа I 4 г
а уравнение профиля производящего исходного контура запищется в следующем виде
COS-J(4)
сс, - lcos(f
- ( 4: 1 4 .3)
Ха
Вводя обозначение
jf: K -21-Z1,
Ха
уравнение (4) можно записать как 40v.4.fJ (6)
V i/Щ/чг 1
К lcos(-| -Ь кх)
Иосле преобразований уравнение (6) .можно привести к виду
COSKX - SIHKX
Учитывая, что нри (4) следует
СПЙ
J JХаI .-- (
ha -J
У-, tsinaa I
-d.
Из уравнения (8) можно определить величи-ну Хдкак
(9)
p-|CosT | %1пая 1
Уравнение (7) и соотношения (5) и (9) определяют профили головок и ножей зубьев производяшего исходного контура. При вычислении координат профиля ножек в оотношение (9) величину ha и в уравнение (7) величину х следует подставлять со знаком минус. На чертеже ведичины х, у, ха, ha и радиальный зазор с выражены через коэффициенты х, , ha, с и модуль зацепления т.
Профили зубьев колес передачи определяются как огибающие кривые профилей зубьев производящего исходного контура при зацеплении нарезаемого колеса с инструментом. Пусть заготовка нарезаемого колеса расположена так, что занимает место колеса- 2, ось ее вращения совпадает с осью вращения этого колеса. С заготовкой (колесом 2) жестко связана система прямоугольных координат Х2О2У2, начало которой совпадает с осью вращения колеса 2 (не изображена). На оси вращения колеса 2 также находится начало неподвижной системы координат хоО2уо (не изображена). Задача определения координат профилей зубьев колеса 2 рещается в три этапа. Применительно к зацеплению производящего исходного контура с колесом 2 на первом этапе следует определить координату х в системе координат хПу, жестко связанной с производящим исходным контуром, при которой точка А профиля будет являться точкой контакта. В данном случае можно задаться, координатой X, а координата у определится из уравнения (4) или из уравнения (7) и соотнощений (5) и (9). На втором этапе определяются коодинаты точки контакта в неподвижной системе координат хо02Уп. Координата Хб определится, если найти точку пересечения нормали, проведенной через точку А осью Пх, а координата Уо определится путем переноса начала координат из полюса П в точку О2, расположенную на оси вращения второго колеса (не показана). Тогда имеем,
(10)
УО У - Г2 -(11)
На третьем этапе определяют координаты профиля колеса 2 в системе координат Х2О2У2, жестко с ним связанной. Для этого используют формулы поворота осей координат
Х2 ХоС05ф2 + УоЗ{Пф2 j(12)
У2 -Хо51Пф2 + уоС05ф2. (13)
Величина угла поворота колеса 2 из начального положения в положение, при котором точка будет контактной точкой, определится из уравнения
dy
:i4)
в котором Г2 радиус начальной окружности колеса 2.
Сделав преобразования под знаком логарифма в уравнении (7), получим
5ч ,.
у - rtjcosKx - sinKx. (15)
Дифференцируя уравнение (15), имеем
dy COSKX -f sinKx , ,п ч ,,-4 10-Тх COSKX sinKX -ctg(4-Kx). (16)
Подставив уравнения (15) и (16) и уравнения (10) и (11), имеем
-:Tctg(-Kx)ErifcosKX-sinKxj; (17)
15
КЧI
EtijCOSKX - sinKx - Г2
(18)
Величина ф2 после подстановки уравнений 20 (16) и (15) в уравнение (14) определится какj
ф2 )lnjCOSKX - SinKXJ.
Произведя вычисления по уравнениям (17), (18) и (19) и подставив значения величин хо, УО, ф2 в уравнения (12) и (13), можно определить координаты профиля зубьев колеса 2. Для удобства записи уравнений (12) и (13) сделаем более общие обозначения. Тогда уравнения (12) и (13) примут вид
(20)
X асовф + вз{пф ; (21) Y -а51пф -+- всозф.
Передача работает следующим образом.
При вращении колеса 1 против часовой стрелки его зубья контактируют с зубьями колеса 2 на линии PzPi зацепления, и колесо 2 получает вращательное движение по часовой стрелке.
Формула изобретения
Зубчатая передача с линейным касанием зубьев, содержащая колеса, профиль зубьев которых выполнен криволинейным, угол профиля зубьев переменный с максимальным значением в точках профилей, расположенных на делительных окружностях, совпадающих с начальными окружностями, отличающаяся тем, что, с целью повышения несущей способности и долговечности, кривая в прямоугольной системе координат с началом координат, расположенной на оси колеса, определена
Х асо5ф-|-в51пф; Y -азтф+всозф,
где величины а, в, ф определены из соотнощенийа 4 1Псо5кх-sinKx|ctg(кх); - In/cosKX-sinKX/-г; х--i-ln|cosKX-sinKx|ctg( где X - независимый параметр, имеющий размерность длины и изменяющийся от -Ха до Хд, ) --,Ь ;(1- a - высота головок главных профилей зубьев колес; зубьев колес; а - постоянный параметр, значения которого лежат в пределах 0,349- - 0,524; г-радиус делительной окружности.

| название | год | авторы | номер документа |
|---|---|---|---|
| Зубчатая передача | 1983 |
|
SU1116245A1 |
| КОСОЗУБАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 2002 |
|
RU2222738C1 |
| СПОСОБ НАРЕЗАНИЯ ЗУБЬЕВ НЕЭВОЛЬВЕНТНОЙ ШЕСТЕРНИ ЦИЛИНДРОКОНИЧЕСКОЙ ПЕРЕДАЧИ ВНУТРЕННЕГО ЗАЦЕПЛЕНИЯ | 2008 |
|
RU2364480C1 |
| Червячная передача | 1983 |
|
SU1128020A1 |
| ПРЯМОЗУБАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 1999 |
|
RU2160403C1 |
| Способ изготовления зубчатых колес | 1987 |
|
SU1662775A1 |
| ЭВОЛЬВЕНТНАЯ ЗУБЧАТАЯ КОРРИГИРОВАННАЯ ПЕРЕДАЧА ВНУТРЕННЕГО ЗАЦЕПЛЕНИЯ | 1991 |
|
RU2025614C1 |
| СПОСОБ ОБРАЗОВАНИЯ ЗУБЧАТЫХ ПЕРЕДАЧ ДВУХПОЗИЦИОННЫМ ОБКАТОМ | 2009 |
|
RU2412026C2 |
| ЭВОЛЬВЕНТНАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 1999 |
|
RU2160858C1 |
| Спироидное зацепление | 1980 |
|
SU937827A1 |
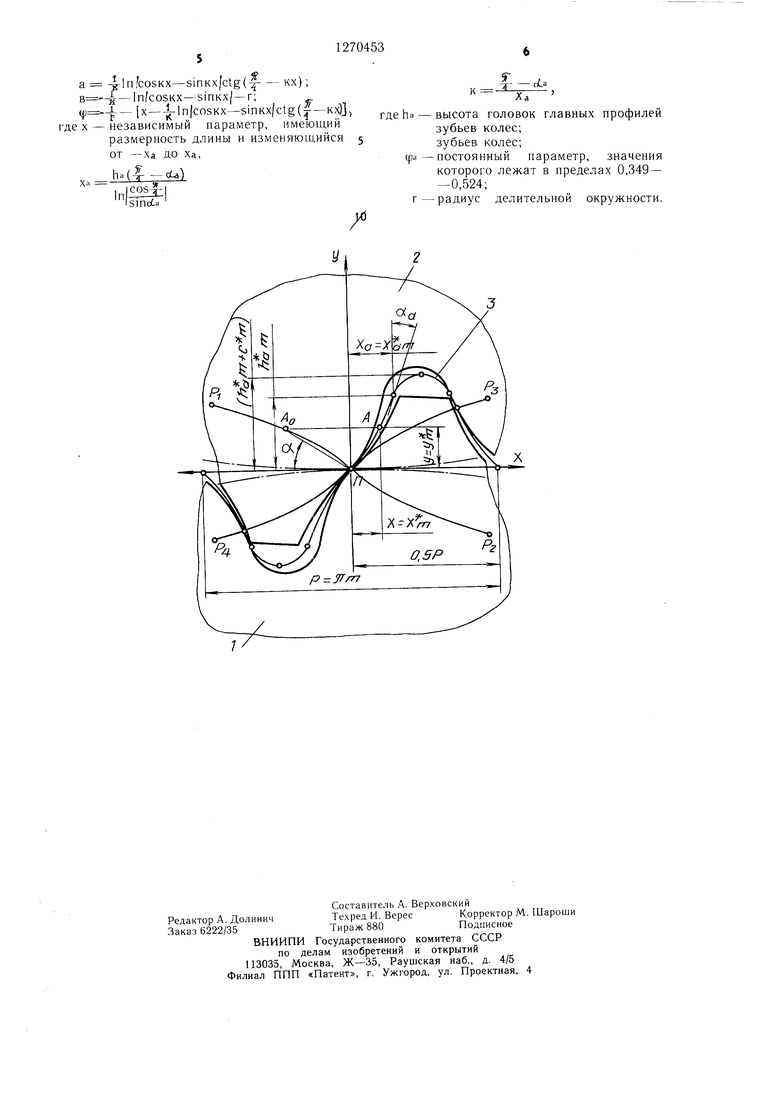
Изобретение относится к машиностроению и может быть использовано в различных отраслях машиностроения в передаточных механизмах. Целью изобретения является повышение несущей способности и долговечности передачи за счет равномерного изменения направления линии действия реакции в высшей паре. В зубчатой передаче с линейным касанием зубьев профиль последних выполнен криволинейным у колес 1 и 2. Угол профиля зубьев переменный и имеет максимальное значение в точках профилей, расположенных на делительных окружностях, которые совпадают с начальными окружностями. Профиль зубьев колес описан кривыми, определенными из условия изменения угла профиля зубьев по линейному закону и функции угла поворота колес. При работе передачи пересопряжение зубьев колес 1, 2 осуществляется по линии зацепления Р|ПР2. 1 ил.


| Зубчатая передача | 1983 |
|
SU1116245A1 |
| Устройство для электрической сигнализации | 1918 |
|
SU16A1 |
Авторы
Даты
1986-11-15—Публикация
1984-12-10—Подача