25
Изобретение относится к вычислиельной технике и может быть использовано в измерительных и вычислительных устройствах.
Цель изобретения - повышение точ- с ности преобразования за счет уменьшения динa шчecкoй погрешности и дисерсии результата преобразования,
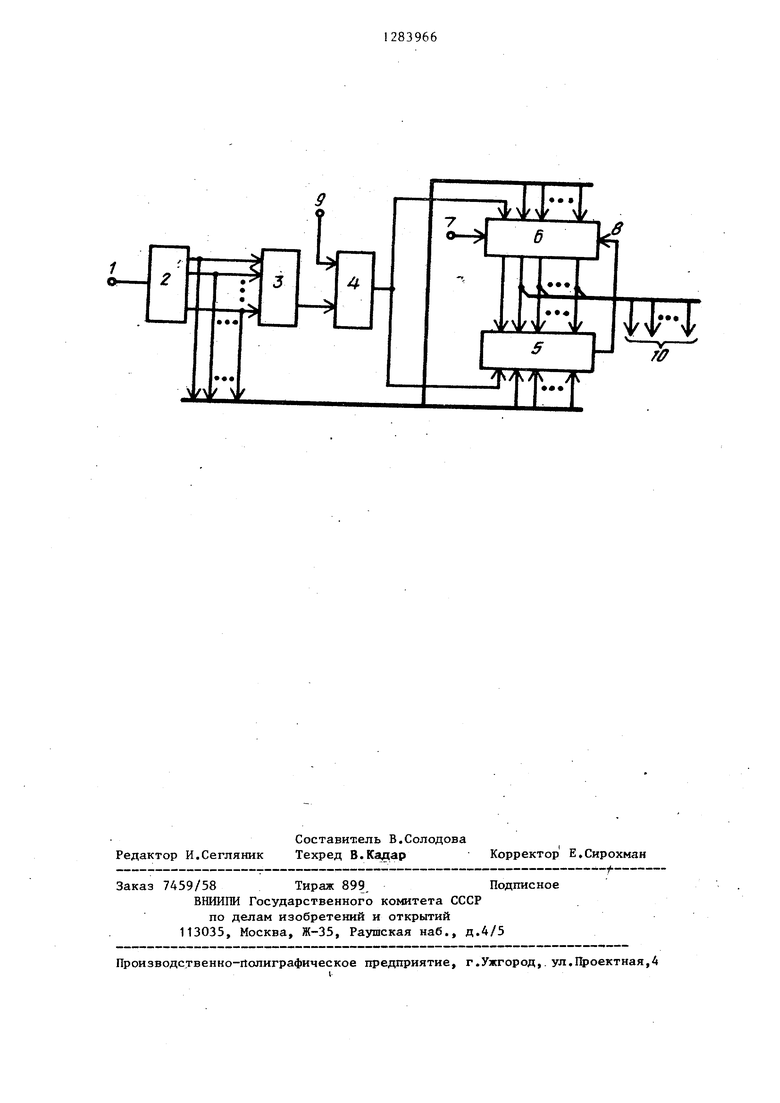
На чертеже представлена блок-схема стохастического аналого-цифрового 10 преобразователя.
. Устройство содержит шину 1 синхронизации, генератор 2 случайных чисел, цифроаналоговьй преобразователь 3 компаратор 4,блок 5 сравнения двоич- 15 ных чисел, регистр 6 со входом 7 начальной установки и входом 8 управле- }шя записью информации, входную шину 9 и выходную шину 10.
Шина 1 синхрониза1дии подключена 20 к управляющему входу генератора 2, выходы которого соединены со входами цифроаналогового преобразователя 3, выход, которого соединен с первым входом компаратора 4, второй вход которого является входной шиной 9. Выход компаратора 4 соединен со входом старшего разряда регистра 6, к остальным входам которого подключены выходы генератора 2, Выходы регистра 6 соединены с первой группой входов блока 5 сравнения двоичных чисел, выход которой подключен ко входу 8 управления записью информагщи в регистр 6, имеющий также вход 7 начальной установки, который является входом установки начального состояния устройства (в единичное состояние всех разрядов регистра 6, за исключением старшего разряда, устанавливаемого в ноль),
Ко входу старшего разряда второй группы входов блока 5 сравнения двоичных чисел подключен выход компаратора 4j .а к остальным входам второй группы входов блока 5 сравнения двоичных чисел подключены выходы генератора 2. Выходы регистра 6, за исключением старшего разряда, являются выходной шиньй 10 устройства.
Устройство работает следующим образом.
В каждом такте под действием импульсов синхронизации генератор 2 вьфабатывает случайное число, кото- 55 рое с помощью цифроаналогового преоб- разователя 3 преобразуется в случайное напряжение, поступающее на первый вход компаратора 4, на второй
35
30
40
-
50
вход 9 компаратора 4 подается входное напряжение U. Если случайное напряжение на первом входе компаратора 4 меньше, чем входное напряжение Ujj на втором входе компаратора 4, то на выходе компаратора 4 вырабатывается сигнал логической единицы.
В начале преобразования регистр 6 переводят в начальное состояние логической единицы во всех разрядах регистра 6, за исключением старшего разряда, устанавливаемого в ноль, подавая соответствукяций управляющий сигнап на вход 7.
В первом такте работы двоичное число с выхода регистра 6 с нулевым старшим разрядом и единичным состоянием остальных разрядов поступает на первую группу входов блока 5 сравнения двоичных чисел, на вторую группу входов которой подается число
х+
-1-«.
где Ч - бинарный
25
0
символ с выхода компаратора 4 в первом такте; Н - случайное число с выхода генератора 2 в первом такте работы.
На выходе блока 5 сравнения двоичных чисел вьфабатывается сигнап логической единицы в том случае, если число, находящееся в регистре 6 и поступающее на первую группу в ходов блока сравнения двоичных чисел,больше числа, поступающего на вторую 35 группу входов блока сравнения двоич30
ных чис ел, т.е.
П -н -1- 1 2
Н,, где i 0
55
40
номер такта. В противном случае на выходе блока 5 сравнения двоичных чисел вырабатывается сигнал логического ноля,
При появлении сигцала логической единицы на выходе блока 5 сравнения двоичных чисел в такте j на вход 8
управления записью информащш регистра 6 придет активный сигнал за- - писи информации, таким образом, в регистр 6 будет записано число nj- - I 1
50
При нулевом состоянии сигнала на выходе блока 5 сравнения двоичных чисел в такте j состояние регистра не изменяется и равно состоянию его
Г
предыдущем такте
1-../
-I- .:,
В первом такте работы устройства на выходе блока 5 сравнения двоичных чисел всегда будет состояние
в регистр 6 запищется
V -г /
312839664
логической единицы, таким образом. Рассмотрим теперь работу схемы в
первом такте. В табл. 2 сведены возможные входные воздействия и соответ- В остальных тактах устройство ствуюпще им выходные состояния для работает аналогично.-д устройства, реализующего как показаТаким образом, в pet HCTpe 6 в но фз нкцию ксинимум, в первом каждом такте i находится минимальное работы.
.+ - Н- и . + ( 2 t 1-1
, а на выходной шине 10 -
из чисел
-I-,-,
удвоенное значение этого минимума.
Докажем теперь, что устройство производит требуемое преобразование
Для этого определим, математическое ожидание числа, вьщаваемого на выходную шину 10 в определенном такте t работы устройства.
При этом считаем, что случайная последовательность с выхода компаратора 4 подчинена распределению Бер- нулли.
Для простоты и наглядности рассуждений обратимся к примеру работы схемы с трехразрядным генератором 2 случайных чисел и будем считать, что X 3/8, где X - двоичный эквивалент и. В табл. 1 даны соответствия выходов компаратора 41. всевозможным случайным числам с выхода генератора 2 для заданного U - X 3/8.
Таблица 1
Здесь и далее считаем, что двоичные числа с выходной шины 10, а также . и лежат в интервале от О до 1.
Таблица 2
15
20
.
30
Математическое ожидание числа, поступающего на выходную шину 10 в
,г первом такте,равно
i Zf
1)
Z.p.
1
(1)
где Z - число с выходной шины 10; t - номер такта; t. разрядность преобразователя
аналог-код; i - номер возможного состояния
выходной шины 10; р. - вероятность появления Z .
на выходной шине 10.
Поскольку любое из возможных сйс- ; тояний шины 10 равновероятно, то
01 ,1
5
i F Отсюда M(Z, t 1)
М
(2)
1
м
irM
.i.f
2 fnZ,
(3)
ы
Для данного числового примера
. „(z,t.,).-i-(-|- + . -I- -I- -I- -I- -i-
8.4-(-i-l . 7 ... 7
8 8 8
+ i) + 3.---1
l.. 8 + ( L + Л.
OLO ° Q Q
8
.|..
8
8
8
+ - +
й) -о +
12839666
,. (.6. .Z.
8 ,-,8 8 8 8
н- -I ,. .
Соответственно дхгя любого X
ч-1
M(Z, ) X +
M
Ji.a.t.
M
(.)
Возможные состояния во втором такте работы устройства показаны в табл, 3, откуда видно, что
М M(Z, ) -I IZI
Таблица 3
Z.
(5)
Для конкретного числового примера Ш, (-l- 5 -l- n .5.п.|-,9. ..IKS.
3 + 1)
.1.3,.(8. -70+-.( 5 /,„ . 6
4 б
6) + -.(6 - 5М + (5
.
40
Для любого заданного X запишем
М-1
M(Z, ) X + - -- рг--- (6)
После анализа возможных состояний ;В третьем такте работы устройства получаем /,.
.(
. 45 1M(Z, ) X + ..
(7)
( - 3) + -1- (У - 2 +
оо
2 -1 +1 - 04
-(7 +52 +52 + 4 ) - - 32 + оо
Z 3 1 -I- I --- . 8 3fiA L я
1 8
3 „, .
2 +
32 +
По индукции запишем выражение ,дпя математического ожидания резуль. тата в любом такте „, . 50
Н-1М-1
Е У
Y
M(z.t) x
PF
--)( +
Е:ХМ 1
М
t-t-i
Отсюда видно, что tim M(Z,t) X,.
.
(в)
(9)
что доказывает вьтолнение предпагае- лой схемой заданного преобразования.
Преобразуем теперь выражение (8) в удобную для его вычисления форму. Для этого рассмотрим член вьфажения (8), равный
Et
М-1
«1
lit
iMilll j: iM-2/ +.,,.i(XM+;l)
Mt
(M-rf + (N-2)+.. . + (ХМ+1-М+М)
, (1 ) (1 --|-)Ч ... .
n - ч 1 М Очевидно, что1
--й- -1 --й-П
Известно, что
tim (1 - -1-) е- М-со М
-IT
Тогда
1 ,t
fiffi (1 - -) е
Отсюда получаем
М-1
t
М
(10) (11)
(12) (13)
Z
Е
.fim е М-со
at
тзг
(М -xM-iH
+ е + ... + е
Выражение (14) представл геометрическую прогрессию
/ , , М-ХМ -1 .
а(1+а+а2+а +...+а ),
t м где а е
Сумма ее равна
1-а
М-,ХМ-1
(1-а ),
Тогда м-1
tim
М-.ОС, - М
t
|И
(M-xw-i)t
(1-е
). (15)
-()
Для достаточно больших матетическое ожидание результата на
.
1283966 10
выходе преобразователя в такте t записывается в виде
1 р
M(Z,t) X + - -тт---гт-« М (, 1 -е -в)
-(м -хм -i)t
(1 + е )Х+В,
(16)
где В - динамическая ошибка.
Известна зависимость математического ожидания результата на выходе следящего интегратора в известном устройстве от числа тактов t t
.t) X - X-e X - XR , O7)
В этой формуле XR является динамической ошибкой.
Найдем отношение динамических ошибок, имеющих место в предлагаемом и известном устройствах.
(M-XM-)|t
(1-е
ХМ d-e )
(18)
Учитьшая, что число тактов работы следящего интегратора обычно выбирается равным
30
t 2 In 2 - М- tn М
(19)
получаем
А .-I- (-1- - -.1- ) X М - М2
(20)
Отсюда видно, что 11
А i 1, для
сех - --Г . т.е. для всех
М М
озможных X.
Таким образом, предлагаемый стохастический аналого-цифровой преобразователь обеспечивает меньшую динамическую ошибку для всех X (U) по сравнению с известньм устройством.
В среднем для X, распределенных равновероятно и равномерно в интервале от О до М-1/М, в предлагаемой схе- ме достигается уменьшение динамической ошибки а раз, где
- TiLf TT
м-ТТ
2М
М
м
2М М-Т
() (М-1) „ м5(м-ТУ
т.е. в два раза меньше.
111283966-п
Оценим теперь дисперсию результа-м -i
та в такте t на выходе предлагаемого (2М+2ХМ-1)Е
устройства Х +i-
D(Z,t) E(Z,t) - M4Z,t) (21) -5
,2 fcKM + i
-....«. .
где E(Z,t) - второй начальный момент, М (24)
равньйТогда
1 Д 1
(2) Г- (22) 10 D(Z,t) E(Z.t) - M2(Z,t) - И-1
Проанализировав табл. 2 и 3, мож- (2М+2ХМ-1) с xM-t-l но записать для описанного примера + GFмТ-
E(2,t).- T fC-|-) 8+ (-|-) -7 +(-|-).7 -и-1
- (4-,а.б . (4-)-б - (-5-) -5 . ir - -- -q i-х V
.()..зч (-|-).4Ч (4-)-4 ° -8-;-5 . (-g-).4--. (-g-)-4 Yin: I
i. И-)8Ч((4
2X 1 / E XM+1 x Z 4т (-i-) вЧ ((4- ) - ЙТ й й
- ( 3)a).7 , a-f-) - (-l-ne . ZZZI
(2M-1) H-1
6 5..
.((-|-)a (-|-).).5t,
ЭПM-tM-1
7 ,.6 „, ,t 30rt f
,(-.,- (.2-).,.4., ,y
M2 Mt M- M /
Запишем это в общем виде (25)
v(7 t) - --- ГХ2 М + 35 Представим вьфажение (25) в удобMtчой для вычисления по аналогии
. .. оумол- + представлением вьфажения (8) в ни ) (м-1) (М-2) -ьде (16)
(y-M-i)р
, (2XLi±3) (м-3) . ... .4o:D(z.t) ..J,,. , „
(M-xM-t)t
, (2Mll).(XM) (23) .(1-е ).
-t + i (M-xM-iK-t -i)
Г,MM
Отсюда получаем, Ь П - о)
7УМ t (1-е)
E(Z,t) -1-г { + ---- Щ (M-xyi-Dt
М Б--ХМ-1., е JT .
(м-1 f . з(м-2) . () --
+ 5(М-3) + ... + (2М-2ХМ-3)(ХМ)Отсюда видно, что
, м-1 . ; ч-t
2ХМl-r, D(Z,t) О
Х2 + -±ii b - xjlii+ „
- (27)
м-tДисперсия результата на выходе
). г(2М-2Е-1) Е следящего интегратора известного
1 „1. устройства даже при t- « имеет
М М конечное значение и не достигает ну13
ля. Дисперсия на вых интегратора равна
D(Z,t
) )
st (Х2+Х) е .
Откуда получаем
Mii5l
м
(29)
Для сравнения D(Z,t) и D (Z,t) найдем Их отношение
Тогда
(ха-х)( - -1. )
.
о , - - -- е М2 М
().-М е ХМ
ХМ 277357
(33)
л. 2
2 + --- е
I Отсюда видно, что | 1, когда X 2,7/М, т.е. дисперсия результата на выходе предлагаемого преобразователя аналог-код меньше дисперсии результата на выходе известного устройства для всех X , кроме и « 2/М.у Причем, чем больше значение входе, т.е. чем больше X, тем больше .
В среднем для X , распределенных равномерно и равновероятно в интервале ОТ О до М-1/М, предлагаемый
1283966
14
преобразователь обеспечивает уменьшение дисперсии результата в раз iB сравнении с известным устройством,
где
М
2(2+ - ) е
(34)
Так, например, восьмиразрядная схема предлагаемого стохастического реобразователя дает среднее уменьение дисперсии результата в 46,6 аза по сравнению со схемой известного устройства для X , распределен- ньк равномерно и равновероятно в ин- тервале от О до М-1/М.
Формула изобретниия
Стохастический аналого-цифровой преобразователь, содержащий блок сравнения двоичных чисел, последовательно соединенные генератор случайных чисел, цифроаналоговый преобразователь и компаратор, второй вход
которого является входной шиной, а вход генератора случайных чисел соединен с шиной стробирования, отличающийся тем, что, с целью повьппения точности преобразования за счет уменьшения динамической погрешности и дисперсии результата преобразования, в него введен регистр со входом начальной установки, который является входом установки начального состояния устройства,
выходы которого соединены соотвегст- венно с первой группой входов блока сравнения двоичных чисел, ко входу старшего разряда второй группы входов которой подключен выход компара
тора, а к остальным входам второй группы входов блока сравнения двоичных чисел подсоединены соответствующие выходы генератора случайных чи45 сел, выход блока сравнения двоичных
чисел подключен к входу управления записью информации регистра, информационный вход старшего разряда которого соединен с выходом компарато50 ра, а остальные информационные входы регистра соединены с соответствующими выходами генератора случайных чисел, выходы регистра, за исключением старшего разряда, являются соот
55 ветственно выходными шинами о






| название | год | авторы | номер документа |
|---|---|---|---|
| Вероятностный интегрирующий преобразователь аналог-код | 1987 |
|
SU1441476A1 |
| Стохастическое устройство для возведения в целую степень | 1981 |
|
SU962941A2 |
| Коррелятор | 1984 |
|
SU1180927A1 |
| Генератор псевдослучайных чисел | 1981 |
|
SU962935A1 |
| Стохастический аналого-цифровой преобразователь | 1986 |
|
SU1332529A1 |
| УСТРОЙСТВО ДЛЯ ДЕТЕКТИРОВАНИЯ ГРУПП ЕДИНИЧНЫХ БИТ И МАКСИМАЛЬНЫХ ГРУПП В БЛОКАХ БИНАРНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ | 2023 |
|
RU2815502C1 |
| Стохастическое вычислительное устройство | 1982 |
|
SU1062700A1 |
| Аналого-цифровой преобразователь | 1985 |
|
SU1336237A1 |
| Преобразователь активной мощности в цифровой код | 1989 |
|
SU1780033A1 |
| Генератор случайных чисел | 1981 |
|
SU1008737A1 |
Изобретение относится к вычислительной технике и позволяет повысить точность преобразования аналог- код за счет использования дополнительной информации о характеристиках вспомогательного случайного процесса от генератора случайных чисел (ГСЧ). При этом аналоговый сигнал U,,, на входе преобразуется с помощью компаратора, на второй вход которого подает- ся случайное напряжение с выхода циф- роаналогового преобразователя, на входы которого поступает случайное число с выхода ГСЧ, запускаемого сигналом синхронизации, в последовательность бинарных символов vj. с вероятностью появления единицы, равной значению входного аналогового сигнала и . В регистр, последовательно соединенный с блоком сравнения двоичных чисел, в каждом i-м такте записывается минима,пьное из чисел ( + 1/2 Н, и П. + 1/2 Н., , где - бинарный символ с выхода компаратора, а Н,-. - случайное число с выхода ГСЧ в тактах i и i-1 соответственно. Математическое ожидание результата на выходной шине, т.е. ha выходе стохастического аналого-цифрового преобразователя при t- где t - число тактов работы схемы, равно M(Z ) X, где х - двоичный эквивалент U. Повьшение точности преобразования выражается в форме уменьшения динамической ошибки и существенного снижения дисперсии результата в сравнении с прототипом. 1 ил. 3 табл. i (Л tc 00 00 со о: О)

| Билинский И.Я | |||
| и др | |||
| Стохастическая цифровая обработка непрерывных сигналов.Рига: Зинатне, 1983, с.12-15, рис | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Корчагин В.Г | |||
| и др | |||
| Измерение вероятностных характеристик случайных процессов с применением стохастических вычислительных устройств | |||
| Л.: Энергоатомиздат, Лен | |||
| отд | |||
| Устройство для видения на расстоянии | 1915 |
|
SU1982A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1987-01-15—Публикация
1985-07-22—Подача