112
Изобретение относится к автоматике и вычислительной технике, в частности к устройствам дискретного преобразования Фурье сигналов (формирования сигналов) и может найти широко применение для построения параллельных спектральных анализаторов.
Цель изобретения - упрощение устройства.
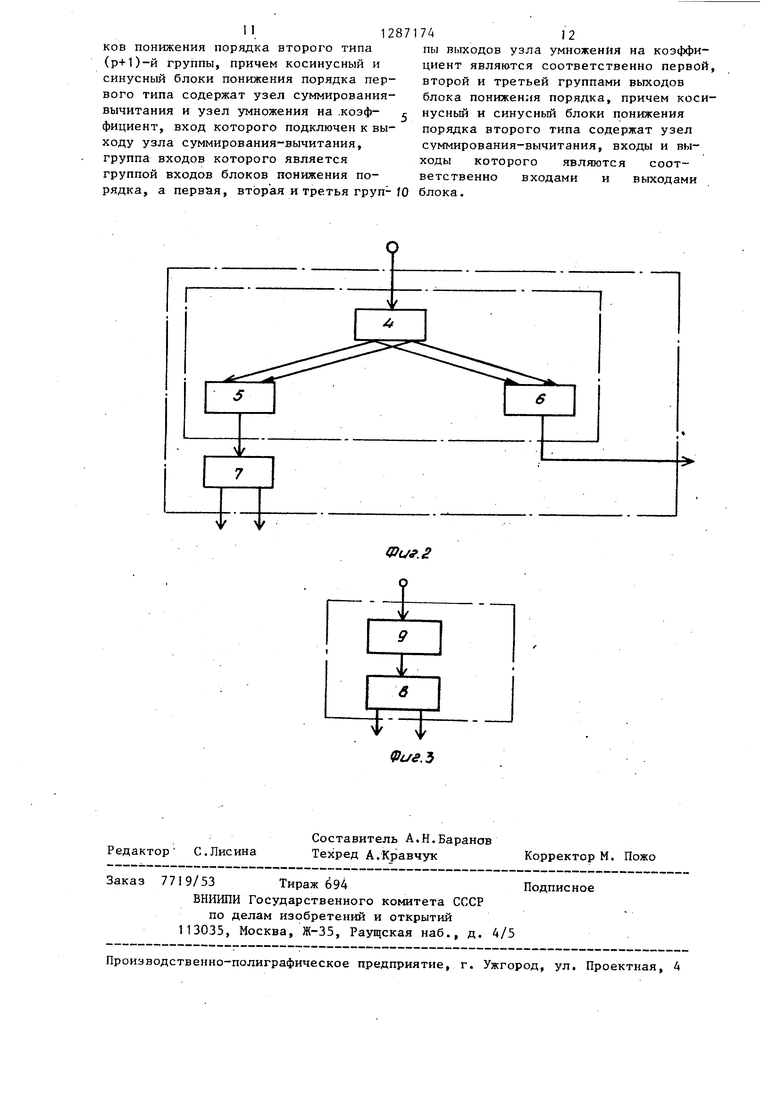
На фиг. 1 изображена блок-схема устройства; на фиг. 2 - блок-схема Косинусного (синусного) блока повышения порядка первого типа; на фиг, 3 - блок-схема косинусного (синусного) блока понижения порядка второго типа
Устройство содержит группы косинусных и синусных блоков понижения порядка первого типа 1,2
и 1-2 -1-2 , группы косинусных блоS
ков понижения порядка второго типа 2 -22-2 -2 и 2g-22-2 -2 и группы 3 блоков суммирования-вычитания.
Косинусный (синусный) блок понижения порядка первого типа (фиг. 2) содержит узел суммирования вычитания состоящий из сумматоров 4 - 6 и узла 7 умножения на коэффициент. Косинусный (синусный) блок понижения порядка второго типа (фиг. З) содержит узел 8 суммирования-вычитания.
Работа уст ройства основывается на следующем алгоритме.
Выражение a(2(2k+1)) для дискретного -синус-преобразования Фурье 2 сигналов обладает следующим свой- ством:.
a(2(2k+1)):i A/l,k)
sirM (1)
где i) 0,1,... ,n; ,1,2,...; 0,1,2,...;
A;(l,k,4)x(l); ,1,...,2 H; AMO,k,4)AV, ( ,k,4)sinll(2k+
+ 1)72 ; A (l,k,)AV, (l.k,W+A, (2;- -l,k,)+2A ,.x( +
.,,,,i, („
,1,.«)2 -I
Соотношение. (l) легко доказывается индукцией по i при любых значениях k и .
Любое целое действительное число из множества, ограниченного интервалом (-2, 2), может быть получено из выражения
74 .2
(2и + 1),
где 0,1,...,п-1; ,1,...,2 -1; ф - знак + или -.
Любое целое действительное число из множества, ограниченного интервалом (-2 , 2), может быть представлено в виде алгебраической суммы возрастающих степеней двойки.
Следовательно, при определенных значениях k и может иметь место равенство
(2k+1) ,.2... ...0..,2,2..., (3) где OioC-i r.. .(0).. .tn.
Для выражения (1), характеризующего дискретное преобразование Фурье от действительной последовательности сигналов х(1) (,1,...,2 -1), при любом k и. справедливы равенства лi
a(242k+1))a(-2 (2k+1));.
a (2.(2k+1))-a4-2(2k+1)). (4)
Определяют способ формирования дискретного преобразования Фурье сигналов х(1). На основании (3) вводят последовательность сигналов ар1 умен- тов
Ф.
Ч : ; 0 „2Ч2 ЧГФ 2%Ыгр.п; t 00o2l5,20,2 ,242
VJ ;0,2 .r.n;
f- , .. . f0-., г .2..2У. ...
2; ... (5) qjj (-Г . . j
. Д-V,
,Z
n 00,2,... ,
: ...2V . 2$. 2... .2
,n ; - . .i
причем 0, 4 of.f, /p, . ., . . . ; e().
Сигналы (функции) a ( V),
fi () f2 1) А/3 Л VV.. , . . . U, I
с учетом указанных свойств и заготовок, использующихся при формировании данных сигналов (функций) от сигналов (аргументов) 4 с меньщими значениями своих индексов, могут быть сформированы циклически.
Нулевой цикл. Сигналы VJ , ..., с учетом (5) можно представить в виде
.();
rO(c.
.0+(Ч Д +0).
Кроме того, учитывая (2) для -V -О,
можно записать
(1,о).л: : сг,.г-:о).
Со) о CIS/
(0)0
Ost CCS)
(f,t.V-0)- (Л -о
. iJ (vS-O)
а (z) 2::А,(1),,.,---:--,
(7)
где ii п. (1)х(1), (6) О Используя указанные свойства и (2),
° СС51(6), закон формирования сигналов а,
т.е. значения сигналов А не зависят
от второго аргумента. Исходя из это- начиная с аргумента „ ° , можно предОо1
можно записать
c(s
с,
ставить в виде
IHC UiQi;
W 0 - - . Г1„- i
0,
0,
(I)L А/ (1,)-, ,.
ыр
Vтu.
-о ,
а-(.,
. 2
где 0,1,
.Ф;
(Vj -0),... через разность (ч -0)
Представляют разности ( f %-0) , .. .. с учетом (5) следующим образом:
«.р
(f,t°-OH(()-()) (4 f
-o)(4 5-o)-.(4,t-4 f;).
OcL
Vz оы.
Кроме того, выбирают такое ,Яk при / 0,1,.. .
сC(S)
чтобы сигналы А . при возрастании
о
второго аргумента не меняли своего значения,, т.е. чтобы были справедливы равенства
).-/;- )
) ф-
, ал
о
35
...А (I,) ... (l,0,(2,+1)),(10) . где k,, 0, 1,.. .; ,1...; oL; --l
Используя (2) с учетом (6), п чают, что l должно удовлетворят условию
0.(11)
Первый цикл. На первом цикле, ря во внимания (9) - (11), закон
ccs). я. мирования сигналов а ( ),
(ffp ),..., (Ч ) можно пре ставить в виде
()iz А. (I);
) ::;« „,-a)3inJ -2-:i|-- i;
2 М.
;(r)i: -A,,«)(4Lz--), .-(„.1„ . па,
где п,) J
A;;;4l)(2,(2k.O)
АГ (1),0 (2k.O)sini- -.
« о-«1о, ccs;
Сигналы А формируются по формулам(2) . при ; ; . ; V о
7174
аЧО) ,„ (I); а,0;
по . . -п
Л
сы, й„, ,,, I(o°d.-0).
а ( v-n --г,
. iJ (vS-O)
а (z) 2::А,(1),,.,---:--,
(7)
„ °
Оо1
0,
(1,)-, ,.
Vтu.
(8)
с,--e
.Ф;
. 2
j -0),..
OoL
(9)
Используя (2) с учетом (6), получают, что l должно удовлетворять условию
0.(11)
Первый цикл. На первом цикле, беря во внимания (9) - (11), закон форccs). я. мирования сигналов а ( ),
(ffp ),..., (Ч ) можно представить в виде
.
« о-«1о(13)
512а.7 1 74
Используя указанные свойства и (2) та , могут быть записаны следую- для сигналов (12), начиная с аргумен- щие формулы:
а(С)&г (,,fS.;-.:;,)cos -j;iif: S),,,
-.4Г «.,;,),ьШ;:1А- 1
a-ч..fJBcosI -2 ;-
,.,A«;4l.))sin ill4-UL-/ (,4)
где ,1,o..;. .
С. -«;;-б).
°rv -M M - 2 Ч Р -Л) (15) А U, vv %d. Vz
Представляют разности (py- ). . {f f - V/ ) - (/ - al° Ь ( Л - 4 (Lp/ - oct разность () Кроме того, выберем такое i ,(16) с учетом (5) следующим образом: чтобы сигналы и при возГф 2 и,ол-Гц,, Л.cfu,,., , .
иг °с dLB DoL рг ooL растании второго аргумента не меняли
.25 своего значения, т.е. чтобы были (Y u, Po) (.p Pi-(o f o ) + (,).; справедливы равенства:
d-f, ОоСoLj} c.j3,.
-){
,2 ° ()) ...;Ч1,2() ... (2Ц+1)); , A;, ; (1,2-Ч/;-%1)) ...ЧТ (I.2( ...A ;;4T,0,(2k, + 1) (17)
, где
k,U,1,...; 0,1,.,.; ,p- ;Q&J.r--),. (18)
1, i or-|9-t „, „ j n 1Второй цикл. На втором цикле для
к. П Z. при л - 5 I , . J
с( S1 W
,, XT ч, ,.,- 35 данных сигналов а С,)
Используя (2) с учетом (15), полу- ctsi
чают что / должно удовлетворятьа ( f.j ),.. ., беря во внимание (16)условию(18), закон формирования имеет вид:
а-Чу./;:: (I);
Р fiF ° .(.Л) 0, 0,
c(s) ( ()соз -2-- Lt - l - A (l)sin.
V7 - ),(jA u;sirx
EL-:: i o4.i&i). (19)
2
.и,-,
C(C) (0)5
A,
-где n n - V, ;
(I)A;; (l,0, .1))ccs21 |. Л- (1,0, (2k, .1)x
. in0(2kii:i)
7rT-i
4::;(l)Ar(l,,.1))).A7 (I,,,(2k,.1))x:
о т 11
. I n0,(). /20-) xsin- h-r --. v2uj
Сигналы AV; , формируются лов () , a (), ..., УЧИ- no формулам (4), (2) при , - ,; тывая предьщущие выводы, можно запи- na i-ou цикле для сигна- сать -следуюиц.й закон формирования: ;
71287.174
(Л-) () Г 1 °
С(5)
а %,
Г Тп ° -(i) +у1 ц1- 0- /0. . с,с, 1Л2 ° - (fLl (%; ) LZ (А,„,. (l)cosJ
scs, . ).. т, А .. sin-- ),
(+J o(ii - 2- где п.п .- J. .формируются на (i-l)-oM цикле, исходя
Значения п Д i-t опреде- JQ выводов по всем предыдущим циклам, ляемые как О .-v./, г-W ... +i,) , аналогично 1 и 2 циклам.
.С ()АГ (L0.-, (2.,,,.l))coslM-lI (-мГ. tl,J ,-,.(2k;., -M))sini - --i2LiIi;
-$- -
Ш ((5;., 2.-42k,., .1)(.,.il) д- (ед-,(2Ь -b1)). (22)
-1 е(с) SCS) ,.
Сигналы А J формируются по из выводов по всем предьщущим циклам, формуле (2), при . ;$ ; аналогично 1 и 2 цикл ам.
.-, . ы . / 25 ... ,
Значения . -( i) .,.+ . )Используя указанные свойства и
, . учитьшая все предыдущие выводы для и , - 2 . при/1 0,1,,,, опре- формируемых сигналов, начиная с аргу- деляются на (1-1)-ом цикле, исходя мента можно записатьc(s; й- -(i/ +y -c .) 0.- (и. )r: (А (1, ());
- . ,-11 (.fi-./rx ,
COS-- - ) (Г, А ,. (1,2
() i
...л,,,.:.„,::-.(а:.::&..),, , ш,
2 ,-...,) „01 , di-1
xvf., -- где i 0,1, ...
С «, (..-,.-..(«,
с («.2- - - - (1).
Далее, если есть аргументы, боль- . (16) и кроме того-, выбирается такое
fit
шие, чем У, (например, учитывая (2), J. чтобы сигналы и А j
ф- d h
имеем: V Ji, .2 , где их при возростании второго аргу,„Ф.,„„ мента не меняли своего знаразности с f , выражаются через разф. ф.чения, т.е. чтобы выполнились
ность ( () аналогично (9), 0 равенства:
А (1.2: -:-Vr ( ( 2k,-H));
(1,2 (.V )) ...A;f (1..,.l), (25)
где k--0,1, ... ; §,0,1,...;. при/ 0,1, ... Используя (2),
4i Z-(в i, +.. . + il., ); ,с учетом (24) получают:
1287174
0$/. Ь-(„ + ...+ ), ), (26) т.е. у , должно лежать в пределах от нуля до значения (i+1)-ro показателя степени двойки без. суммы всех предьдущих ),
(1-)-1)-ый цикл. На (i+1)-oM цикле
для данных сигналов . ), ...
принимая во внимание сказанное, получают закон формирования сигналов;
-Z, «..))cosM.il) „,,« „,
Ka.CZk OJainJl - iii;
о 1 4i
Си (1)АГ (1,0, ..1
x(r,0., H-Osini|-%2k,i1)
))eo
2
h, -1
ССС 5/gl
Сигналы А j j А. ,. формируются
f;i l
ПО формулам- (2), при . ; $ .,; . ; V) ). .
Формула и 3 о б р е т е и. и я
Устройство для дискретного преобразования Фурье, содержащее первую группу из двух блоков суммирования- вычитания, о т л и ч а ю щ е е, с я
тем.
1, что, с целью упрощения устройства, оно содержат п групп косинус- ныз и синусных блоков понижения порядка первого типа (, N - размер преобразования по (2-(-1) (,п) блоков в р-й группе, п групп косинусных и синусных блоков понижения порядка второго типа по (2 -ь2 (-1) блоков в р-й группе и (и-1) групп блоков суммирования-вычитания по ((2-(-1 ) блоков в каждой группе, причем первая группа выхода Р-ГО косинусного блока понижения по- рядка первого типа р-й группы подключена к группе входов (р+1)-го ко- синусного блока понижения порядка второго типа (р+1)-1 группы, вторая и третья группы выходов р-го косинусного блока понижения порядка первого типа р-й группы подключена к груп- пам ВХОДОВ соответственно (р+1 )-го синусного блока понижения порядка . второго типа и (р+1)-го косинусного
С о
0
С,./ .(27)
и далее следующие значения сигнаC{S)
лов а от следующих аргументов с
использованием сигналов А (t)
со),-+аналогично (12), (19), (21) 1,2,...,
i-ro циклов,
где п-;,. - 1/, ;
i1)
)).(2kiil) .0 2 .
428)
0
5
5 0 5
блока понижения .порядка первого типа (р+1)-й группы, причем первая, вторая и третья группы выходов синусного блока понижения порядка первого типа группы подключены к группам входов соответственно (р+1)-го синусного блока понижения порядка второго типа, (р+1)го косинусного блока понижения порядка второго типа и (р+1)-го синусного блока понижения .порядка первого типа (р+1)-й группы, группы выходов i-x (,р) косинусного и синусного блоков понижения порядка второго типа р-й группы подключены к группам входов соответственно i-x косинусного и синусного блоков понижения порядка первого типа (р-|-1)-й группы, группы выходов . косинусного и синусного блоков понижения порядка первого типа р-й группы подключены к группам входов соответственно первого и второго блоков суммирования-вычитания р-й груп- Ьы, группы иыходо суммы и разности первого блока сложения-вычитания подключены к группе входов соответственно первых косинусного и синусного блоков понижения порядка второго типа (рн-1)-й группы, группы выходов суммы и разности второго блока суммирования-вычитания р-й группы подключены к группам входов соответственно вторых косинусного и синусного бло11.12871
ков понижения порядка второго типа (р+1)-й группы, причем косинусный и синусный блоки понижения порядка первого типа содержат узел суммирования- вычитания и узел умножения на .коэф- фициент, вход которого подключен к выходу узла суммирования-вычитания, группа входов которого является группой входов блоков понижения порядка, а первая, вторая и третья груп-/О
7412
пы выходов узла умножения на коэффициент являются соответственно первой второй и третьей группами выходов блока понижения порядка, причем косинусный и синусный блоки понижения порядка второго типа содержат узел суммирования-вычитания, входы и выходы которого являются соответственно входами и выходами блока.




| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для дискретного преобразования Фурье сигналов | 1985 |
|
SU1288717A1 |
| Устройство для дискретного преобразования Фурье действительной последовательности сигналов | 1986 |
|
SU1357974A1 |
| Устройство для определения амплитуды и мощности спектральных составляющих комплексного сигнала | 1985 |
|
SU1309037A1 |
| Устройство для вычисления преобразования Фурье | 1985 |
|
SU1287176A1 |
| Устройство для выполнения преобразования Фурье | 1982 |
|
SU1084807A1 |
| Рекурсивный цифровой фильтр | 1990 |
|
SU1732433A1 |
| Устройство для моделирования линейных систем | 1984 |
|
SU1233182A2 |
| Устройство для вычисления коэффициентов нерекурсивных полосовых фильтров | 1988 |
|
SU1647587A1 |
| Функциональный преобразователь | 1986 |
|
SU1352476A1 |
| Рекурсивный полосовой фильтр | 1984 |
|
SU1287032A1 |
Изобретение относится к автоматике и вычислительной технике, в частности к устройствам дискретного преобразования Фурье, и может найти применение для построения параллельных спектральных анализаторов. Цель изобретения - упрощение устройства. Поставленная цель достигается за счет того, что устройство для дискретного преобразования Фурье содержит группы косинусных и синусных- блоков понижения порядка первого и второго типов 73 1 so 7 72 7 з- з с 1с 2 -1с 2 и 1 2 и 2 и группы 3 блоков су {мирования-вычитания с соответствующими связями между блоками устрой- S ства. 3 ил. (Л ГС 00 Ч 4ib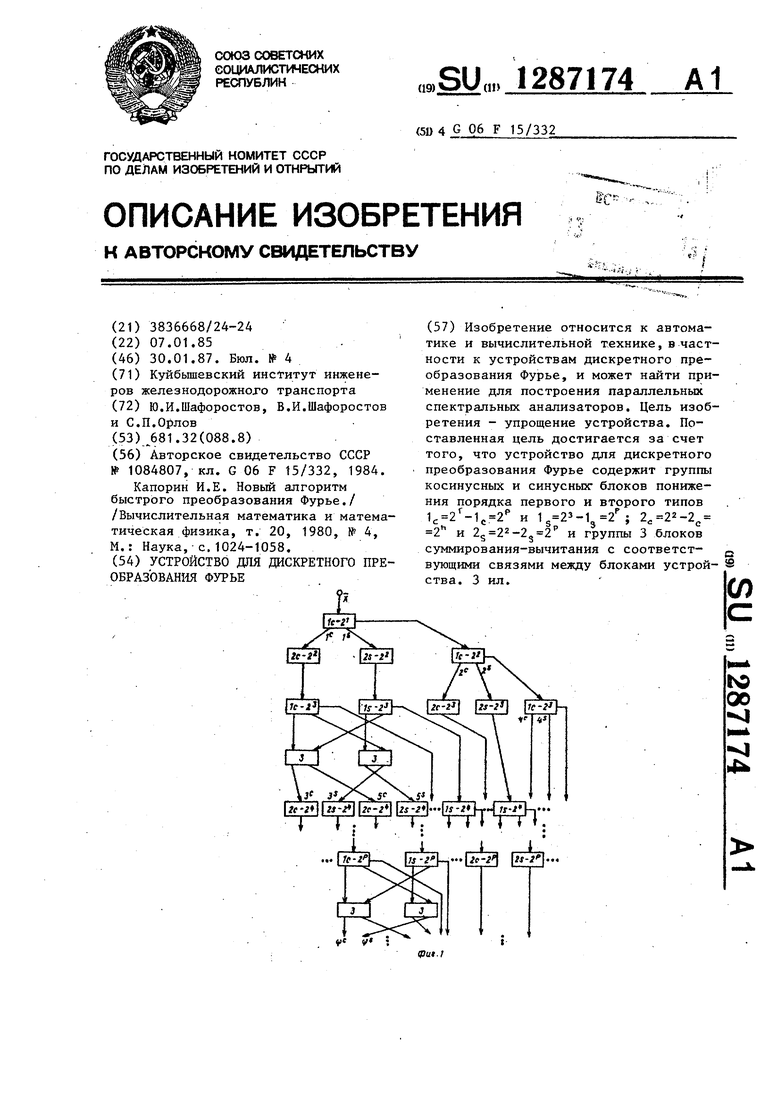
Фс/.2
Редактор С.Лисина
Составитель А.Н.Баранов Техред А.Кравчук
Заказ 7719/53 Тираж 694
ВНИИПИ Государственного комитета СССР
по делам изобретений и открытий 113035, Москва, Ж-35, Раушская наб., д. 4/5
Производственно-полиграфическое предприятие, г. Ужгород, ул. Проектная, 4
Фие.Ъ
Корректор М. Пожо
Подписное

| Устройство для выполнения преобразования Фурье | 1982 |
|
SU1084807A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Капорин И.Е | |||
| Новый алгоритм быстрого преобразования Фурье./ /Вычислительная математика и математическая физика, т | |||
| Прибор для промывания газов | 1922 |
|
SU20A1 |
Авторы
Даты
1987-01-30—Публикация
1985-01-07—Подача