113090372
Изобретение откосится к автомати-ного сигнала (6), который представляке и вычислительной технике, в част-ет из себя функцию дискретного преобности к устройствам для определенияразования Фурье для гармоник целой
амплитудных и мощностных параметровсигнализации при формировании дисспектральных составляющих комплексно- 5кретного преобразования Фурье (7) для
го сигнала, и может широко использо-остальных гармоник,
ваться при построении параллельных Далее, разбивая интервал суммиро спектральных анализаторов.вания в (6) и (7) на два подинтерваЦелью изобретения является упро-ла, получим щение устройства. О , 2
Дпя дальнейших рассуждений исполь- F(2p (;i , (9)
зуют следующие свойства.
Любое целое число из интервала I
0,2 можно получить из соотношения , , , , .
15F((1+4-k) 2 )2
(1+4 k) .
(1)
C;G)-e
Удк 2.
(10)
1VwV 5 Я
Для дискретного преобразования где Cf(i) ZlB(d 2 1)Сь(1)+ Фурье комплексной последовательности +jcl(i) .(11)
сигналов имеет место следующее соот- 7п / ч
„ , „„,,.Выделяя виО) действительную и мнимую
НОШ6НН6
части. получим
F(2-R)F(-R).(2)
Мощности и амплитуды отрицательной F(()-2 )2 и положительной спектральных состав- 25 ляющих гармоник комплексного сигнала равны, т.е.
M(R)M(-R), A(R)A(-R). (3)
Используя свойства (1) и (2), дис- R 2 i;ik 1 кретное преобразование Фурье комплек-30 , . Cg(.i) sin , j сной последовательности сигналов Z(i) можно переписать в виде
, ir;(t4KV 2.
-J-TTTi
)-sin
или
ЛF((1+4k)((1+4k)-2 ) + +jF ((H-Ak)-2b,
(12)
(13)
F((H-4.k)-2b yiZ(i)e , (4)
VS где , Otk62 .
Раскрывая скобки в экспоненциальной функции формулы (4), имеем
где п,. Заметим, что (10), (12) и (13) есть функция дискретного преобразования Фурье комплексной последовательности сигналов Ce(:L) для гармоник, кратньк
(5)
F((1:t4.k)(i)-e
tiO .
тт.;.2
пПе е
Разбивая интервал суммирования в
(5) на 2 подинтервалов и меняя порядок суммирования, получим:
. F(2
F((1j:4 k)- 2
BgOb
(6)
t,M:ll J (7)
B(i)ce
zg.- -vo-e
ot O
Заметим, что значение функции B(i) - есть i-я составляющая комплекс
C;G)-e
Удк 2.
(10)
F(()-2
)-sin
R 2 i;ik 1 , . Cg(.i) sin , j
или
ЛF((1+4k)((1+4k)-2 ) + +jF ((H-Ak)-2b,
где п,. Заметим, что (10), (12) и (13) есть функция дискретного преобразования Фурье комплексной последовательности сигналов Ce(:L) для гармоник, кратньк
40
целой степени двойки.
Мощность и амплитуда любой гармоники с учетом (2) и (3) определяются как - , М ( (1 +4k) 2 ) F ((1 +4k) 2 +
45 ((1+4k)-2 ,(14)
A((1+4k) 2b ((H4k)-2b .(15)
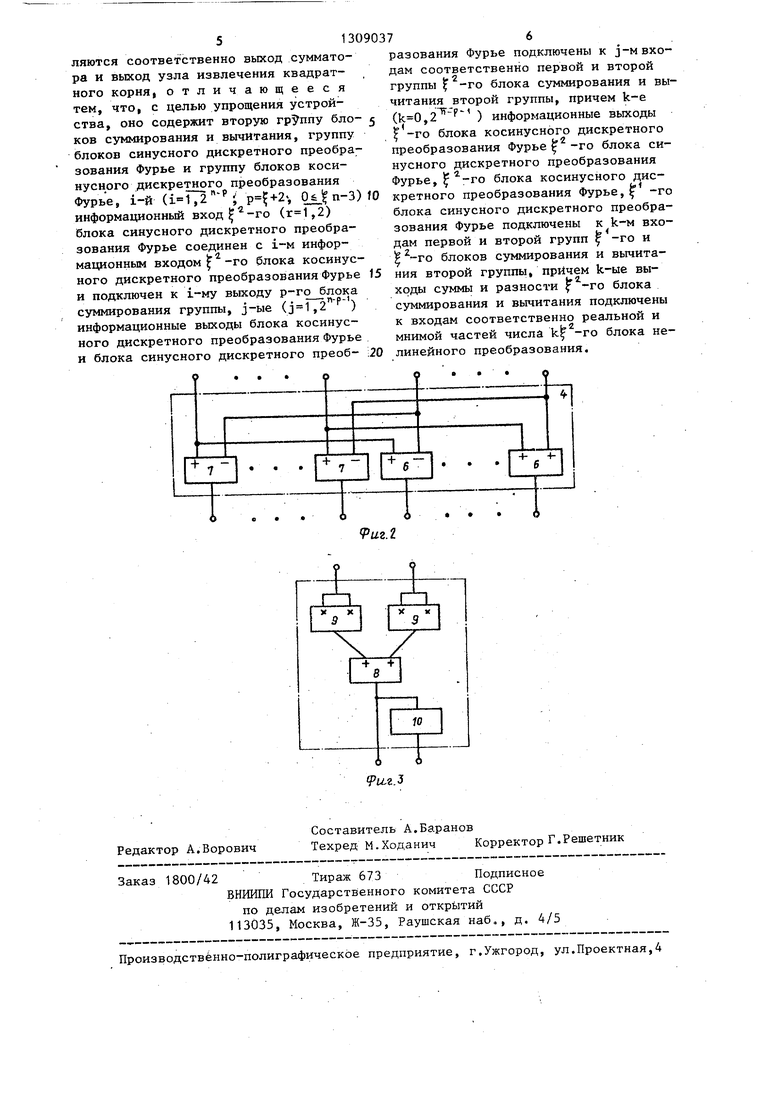
Ha фиг.1 изображена структурная f... схема устройства} на фиг.2 - структура блока суммирования-вычитания; на фиг.З - структура блока нелинейного преобразования.
Рассмотрим схему устройства для , определения амплитуды и мощности
спектральных; составляющих комплексного сигнала.
п-Ярусная схема (фиг.1) имеет две группы по 2 входов, на которые подающие комплексной последовательности сигналов Z(i) () и две группы по ( +1) выходов, на которых формируются амплитуды и мощности спектральных составляющих гармоник входного комплексного сигнала.
Устройство содержит блоки 1 суммирования-вычитания (преобразования
мулам:
Н (k)S(k)+v(k); H(k)S(k)-V(k); ,
и определяют значения дискретного преобразования Фурье для ((l+Ak)
первого рода и блоки 2 суммирования, fO 2)-й и для ((1-4k). 2)-й гармоник имеющие две группы (действительную в формулах (12) и .(13).
и мнимую) по входов и соответ,
Блок 5 нелинейного преобразования предназначен для формирования амплитуды и мощности спектральной состав- , ляющей входного комплексного сигнала и определяет значения сигналов м((1+
ственно две группы выходов, блоки косинусного 3-1 и синусного 3-2 дискретных преобразований Фурье 5 сигналов, имеющие входов и
и Я
2 выходов, блоки 4 суммирования- вычитания алгебраического суммирования, имеющие две группы по 2 входов и две группы по выходов,20 блоки 5 нелинейного преобразования, имеющие два входа и два выхода (р 1,2,...,п, , р - номер яруса схемы).ляющих комплексного сигнала, содерБлок 4 суммирования-вычитания (фиг.2) содержит вычитатели 6 и сум+4k)20 и A((1+4k)-2 в формулах (14) и (15).
формула изобретения
Устройство для определения амплитуды и мощности спектральных составматоры 7. Блок 5 нелинейного преобразования (фиг.З) содержит сумматор
жащее группу из п блоков суммирования (, N - размер преобразования), первую группу из п блоков суммирования и вычитания и N блоков нелинёй- 8, квадраторы 9 и уз.ел 10 извлечения го преобразования, причем i-й вход квадратного корня.30 . (, ) блока суммироБлок 2 суммирования предназначен вычитания первой группы сое- для формирования комплек сной после- входом j-ro блока сумми- довательности сигналов из входной рования группы и подключен к i-му вы- комплексной последовательности сиг- у у,, (j-l)-ro блока суммирова- налов по формуле .35 „цд „ вычитания первой группы, а1-й
выход разности k-ro( ,п-1 j. , блока суммирования и вычитания первой группы подключен к 1-му входу (k+lT- го блока суммирования, а т-й вход (, вход первого блока суммирования и вычитания первой группы является т-м информационным входом - устройства, причем первый и второй выходы S-ro (,N) блока нелинейного преобразования являются выходами соответственно амплитуды и мощности i-й гармоники устройства, при этом блок нелинейного преобразования содержит два квадрата, сумматор и узел извлечения квадратного корня, вход которого подключен к выходу суммато- .ра, первый и второй входы которого подключены к выходам соответственно , первого и второго квадраторов, входы
синусных составляющих в формуле (11). которых являются соответственно входами реальной и мнимой части числа блока нелинейного преобразования, первым и вторым выходами которого яв e4i) e(i)+( +i); Uptn
и определяет значения сумм двух сиг- 40
напов Z(i) и Z( +1) при +1; . п-1 и значении сигналов C(i) (11) в-формулах (9) и (10).
Блок 3-1 косинусного дискретного преобразования Фурье
45
F(k)G(i).cos, . .
Блок 3-2 синусного дискретного преобразования Фурье
( ) HGd). sin ;
и определяет значения косинусных и
Блоки суммирования-вычитания 4 предназначены для формирования двух групп сигналов из входной последова50
мулам:
Н (k)S(k)+v(k); H(k)S(k)-V(k); ,
Блок 5 нелинейного преобразования предназначен для формирования амплитуды и мощности спектральной состав- ляющей входного комплексного сигнала и определяет значения сигналов м((1+
ляющих комплексного сигнала, содер+4k)20 и A((1+4k)-2 в формулах (14) и (15).
формула изобретения
Устройство для определения амплитуды и мощности спектральных составразования Фурье подключены к j-м входам соответственно первой и второй группы -го блока суммирования и вычитания второй группы, причем k-e ) информационные выходы
ляются соответственно выход сумматора и выход узла извлечения квадратного корня, отличающееся тем, что, с целью упрощения устройства, оно содержит вторую бло- 5(,2
ков суммирования и вычитания, группу -го блока косинусного дискретного
блоков синусного дискретного преобра-преобразования Фурье -го блока сизования Фурье и группу блоков коси-нусного дискретного преобразования
нуснрго дискретного преобразованияФурье,-го блока косинусного дисФурье, i-й (,2 J , Ofe п-3) fOкретного преобразования Фурье, -го
информационный вход -го (,2)блока синусного дискретного преобраблока синусного дискретного преобра-зования Фурье подключены к k-м вхозования Фурье соединен с i-м инфор-дам первой и второй групп -го и
мационным входом -го блока косинус- -го блоков суммирования и вычитаного дискретного преобразования Фурье 15ния второй группы, причем k-ые выходы суммы и разности -го блока суммирования и вычитания подключены
информационные выходы блока косинус-к входам соответственно реальной и
ного дискретного преобразования Фурьемнимой частей числа k -го блока неи блока синусного дискретного преоб- .20линейного преобразования.
и подключен к i-му выходу р-го блока суммирования группы, j-ые (,2 )
разования Фурье подключены к j-м входам соответственно первой и второй группы -го блока суммирования и вычитания второй группы, причем k-e ) информационные выходы
(,2
-го блока косинусного дискретного

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для дискретного преобразования Фурье | 1985 |
|
SU1287174A1 |
| Устройство для дискретного преобразования Фурье действительной последовательности сигналов | 1986 |
|
SU1357974A1 |
| Устройство для дискретного преобразования Фурье сигналов | 1985 |
|
SU1288717A1 |
| Устройство для вычисления преобразования Фурье | 1985 |
|
SU1287176A1 |
| Устройство для выполнения преобразования Фурье | 1982 |
|
SU1084807A1 |
| Устройство для моделирования линейных систем | 1984 |
|
SU1233182A2 |
| Цифровой анализатор спектра | 1979 |
|
SU822193A1 |
| Устройство для вычисления коэффициентов нерекурсивных полосовых фильтров | 1988 |
|
SU1647587A1 |
| Рекурсивный цифровой фильтр | 1990 |
|
SU1732433A1 |
| Устройство для выполнения дискретного преобразования Фурье | 1989 |
|
SU1679501A1 |
Изобретение относится к области .автоматики .и вычислительной техники, в частности к устройствам для определения амплитудньпс и мощностных параметров спектральных составляющих комплексного сигнала, и может быть широко использовано при построении параллельных спектральных анализаторов. Цель изобретения - упрощение устройства. Поставленная цель достигается за счет того, что устройство для определения амплитуды и мощности спектральных составляющих комплексного сигиаша состоит из группы блоков 1 суммирования и вычитания, группы блоков 2 суммирования, группы блоков 3-1 косинусного дискретного преобразования Фурье, группы блоков 3-2 синусного дискретного преобразования Фурье, группы блоков 4 суммирования и вычитания и группы блоков 3 нелинейного преобразования. 3 ил. (Л со о 00 2 со I I I
X 7
Редактор А.Ворович
Составитель А.Баранов
Техред М.Ходанич Корректор Г.Решетник
Заказ 1800/42Тираж 673Подписное
ВНИИПИ Государственного комитета СССР
по делам изобретений и открытий 113035, Москва, Ж-35, Раушская наб,, д. 4/5
Производственно-полиграфическое предприятие, г.Ужгород, ул.Проектная,4

| Рабинер Л., Гоулд Б | |||
| Теория и применение цифр овой обработки сигналов | |||
| М.: Мир, 1978 | |||
| Устройство для выполнения преобразования Фурье | 1982 |
|
SU1084807A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1987-05-07—Публикация
1985-12-17—Подача