n- 1
112887172
Изобретение относится к автомати- Далее, используя равенства
ке и вычислительной технике, в част-i . . - /„, ,, , COSC2 +1)Л (2k+1)2 /2 ,. .кости к устройствам дискретного пре-(7)
образования Фурье сигналов, и может t(1) sin -i(2k+1) . 2 /2 , найти применение при построении па- 5 ц. ,
раллельных спектральных анализато- cos(2 -D-fi (2k+1) 2 /2
Цель изобретения - упрощение уст- V / / , (8) ройства и увеличение быстродействия.,
Определим некоторые свойства, ко-}0 , 5). можно записать в ввде торые нужны для дальнейших рассужде- 2 (2k+1 )} b (i) (-1)
„i 1
НИИ.
Любое число из интервала (0,2) ()()
может быть получено из выражения,v
R 242k.1); ,, (1) %гдеЬ,,,( ()-a ();
0,1,...,n-1, ,. i. (10)
aj,,(i)a (i)+a:(2 -i) ,
Дпя косинусного и синусного дис- о i 6 -1
кретных преобразований Фурье дёйст-а , (2 )а (2 ) (ll)
вительной последовательности 2 сиг-20 (i)a(i). налов имеют место следующие соотношения:
( - / Синусное дискретное преобразоваF CR) F (2 -R); ние Фурье действительной последоваF(R) -F(). тельности 2 сигналов X(i ) (i О,
1,..,,2-1) с учетом равенства (1)
: При любых значениях k и v можноимеет вид записать равенство
cosJ- 2-(2 -k-t) + 1) -cos%(2k+ (2k-H),,,
V+130 a --ia 1 (12)
+ 1)/2 . (3) EI X(i)-sinJr i(2k+1)-2V2
1- 1
Косинусное дискретное преобразо- ,,.
. „ „Учитывая то, что
ванне Фурье действительной последо- ,
вательности 2 сигналов X(i) (i sin(2 -i)5i (2k+1)/2
0,1,.., ,) с учетом равенства 35 -sin J i(2k+1), (1) имеет вид
записать в виде
F (2(2k-H)) -,.
(i).cos5Ti(2k.1) 2V- . 40 j t2(2k.1).)
°Учитьшая то, i) з1пЯ .i() - .,где a(i)X(i)-X()j
cos(.) JV(2k-H)/2 - - 4 0,1,...,n-1; ,1,...,
.()
Используя равенства
равенство (4) можно представить вsin( -ilJf (2k+1) 2 виде .,.1 ь 1
.1)l E:a(i) cos Г i.. (2k.: 50 - / ;
.1) °(5)sin( -i)(2k+1)
где а(о)Х(о);. i(2k+1) 2 ,
/.ч 55 равенство (13) можно записать в виде
a(i)bX(i)+X(2 -i)
Hi 2 - -l; 0,1n-1,,1 (2k.1))C (,5)
,..., Ь., (i sinin-i(2k-b1)
n- 1
П Г2- чГ
Ь.,,()а.( )-aj,( - а i)a(i).
- .-1ф
i); 1 s if z - -i;
(17)
(5)
10
(18)
Рассматривают преобразование
(2k+1) J:A(i) sinT5-i(2k+1)/2 ;
i 1
где .. . f5
Вводят соотношения A (i,k)A(i)j 1 6 i J 2.
1, -J+1
A;(i,k)A. (i,k)+A,/2 -i,k)-«- +2-А, (2 +i,k)-cos3T (2k+1)
(.k).
,k) cosTr (2k+1)/2
1 5) i
n
С учетом равенства (3) можно писать A,,,(i Z-k-1)A(i);
A(i,2 -k-1)A,., (i,k) + +A,., (.2 -i,k)-2 A., (
+i,k) cos5t (2k+1)/2
K, -; A-(2
-J
y+1
,,., () -2Aj,,(2 ,k) cosJl (2k+1)/2
Тогда равенство (18) можно записать в виде
п,- )
s 2V2k+1) A(i,k)-sin3 i(2k+ + 1) . (21)
Соотношение (21) доказывается индукцией по V при использовании формулы синуса суммы двух аргументов.. При )П| формула (21) принимает вид
s 242k+1)A (1,k) sin (2k+
+ 1)/2
n. ti
Преобразования (18), а следова- тельно, и (22) можно использовать для реализации равенств (9) и (15). Следовательно, равенства (8)-(11) и (14)- (22) являются теоретическими предпо- сылками для устройства, реализующего дискретное преобразование Фурье дей
10
f5
887174
ствительной последовательности сиг- налов.
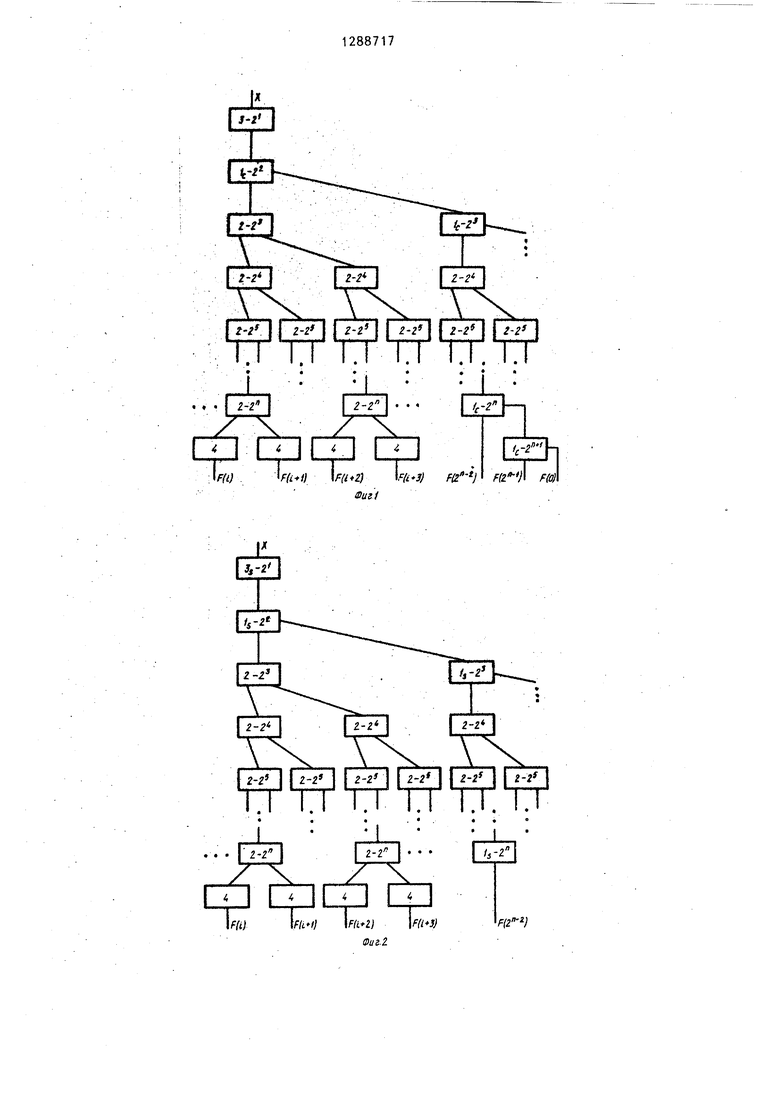
На фиг. 1 и 2 изображены структурные п-ярусные схемы косинусного и синусного каналов устройства для дискретного преобразования Фурье сигналов; на фиг. 3 и А - внутренние структуры блоков суммирования первого рода; на фиг. 5 и 6 - внутренние струк
20
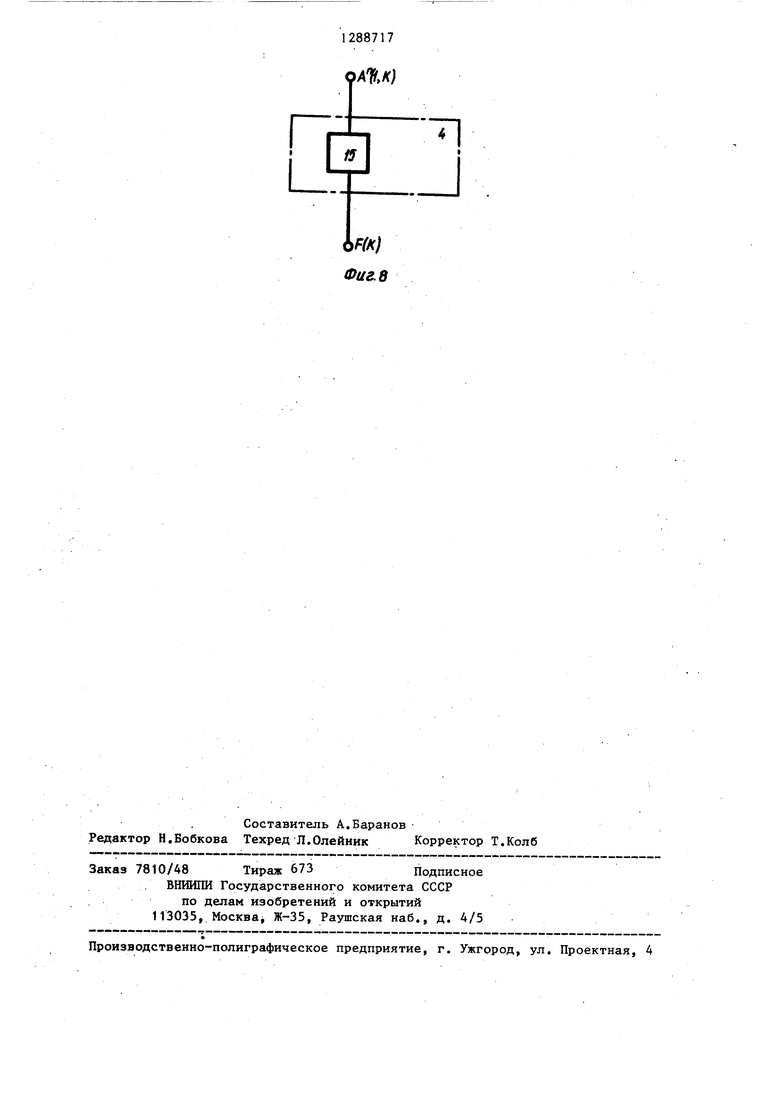
туры блоков суммирования второго рода косинусного и синусного каналов устройства; на фиг. .7 и 8 - -структуры блоков умножения первого и второго родов.
Рассмотрим схему устройства, реализующего дискретное преобразование Фурье действительной последовательности 2 сигналов.
Устройство имеет 2 входов, на которые поступает действительная последовательность сигналов X(L) (,1, ...,), и две группы по 2 выходов, на которых формируются сигналы, соответствующие косинусному и синус- ному дискретным преобразованиям Фурье,, Устройство (фиг. 1 и 2) содержит блок 1 суммирования второго рода, блок 2 умножения второго рода, блок 3 суммирования первого рода, блок 4 умножения первого рода.
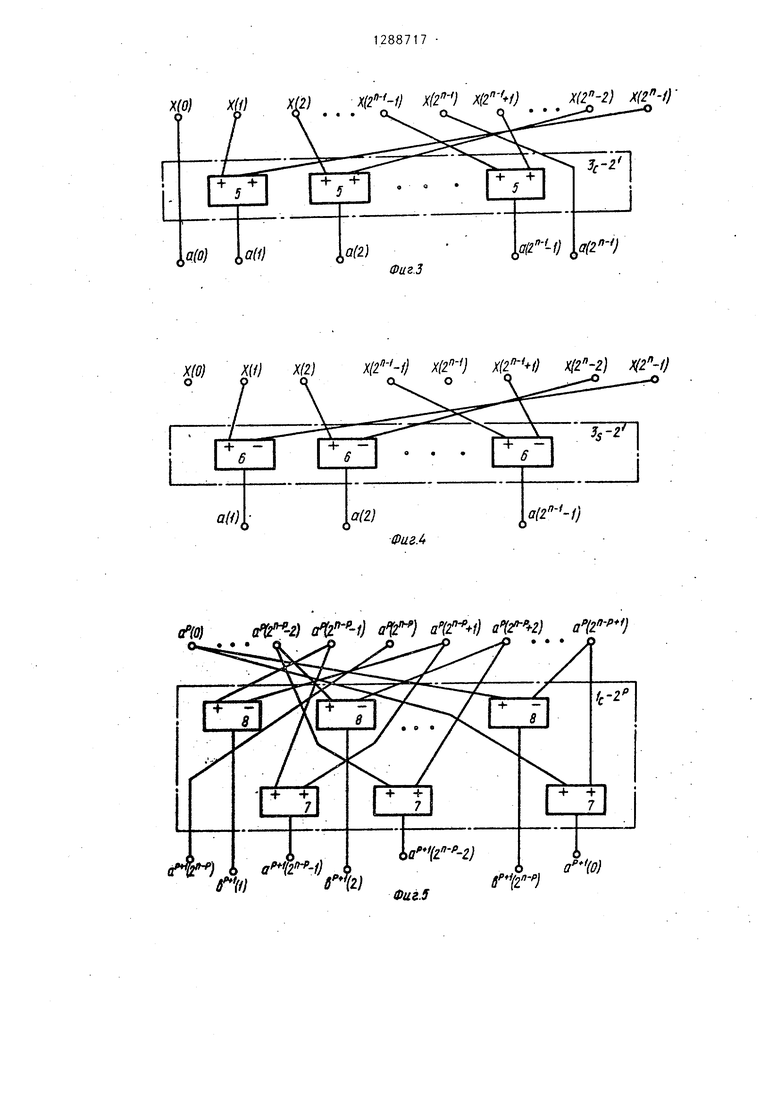
Блок 3, -2 суммирования первого рода косинусный (фиг. 3) и синусный (фиг. 4) состоит из () (двухвхо- довых алгебраических) сумматоров 5 и сумматоров 6. Блок предназначен для формирования сигналов из входной последовательности 2 сигналов по формулам для блока косинусного канала
a(m)x(m)+x(2 -m); m 1,2,... , 2 -1;
а(о)х(о); а( )х( );
для блока синусного канала ,
a(m)x(m)-x(); ,2,... , -1, и определяет значение сигналов a(i) в формулах (8) и (14).
30
35
-40
45
0
5 вательности 2 мулам Блок (фиг. 5) суммирования, второго рода (косинусный) -состоит из
двух групп по (двухвходовых алгебраических) сумматоров 7 и 8. Блок предназначен для формирования двух
из входной последо- сигналов по форельности 2 ам
/
b (m)
(2 - -m)-a();
ельности 2 ам
(m-1))V( -шч-1);
r+1 у„пa -(2 ,2,...,2
)аЧ2 - h-p
);
и .определяет значение сигналов ) и а.,(i) в формулах (10) и (11).
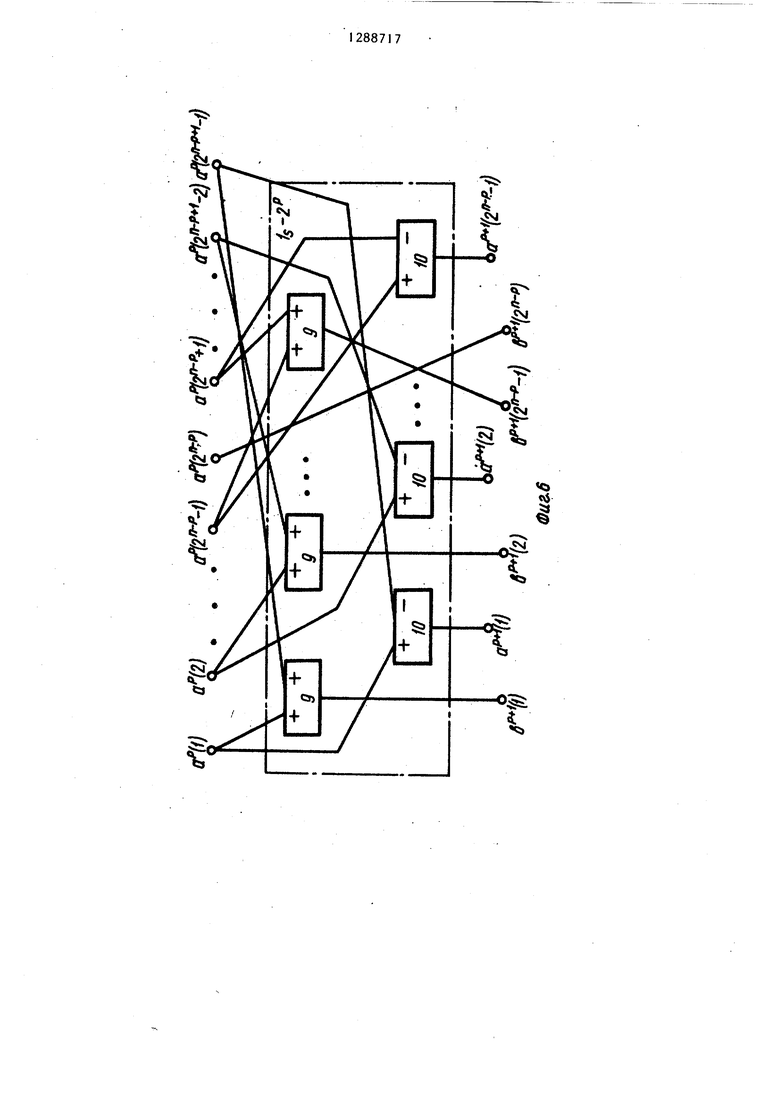
Блок ,j 2 (фиг. 6) суммирования второго рода (синусньй) состоит из двух групп по (2 -t) (двухвхо- довых алгебраических) сумматоров 9 и 10. Блок предназначен для форми- JQ рования двух групп сигналов из входной .последовательности () сигналов по формулам
р+1
b (т)аЧт)+а (2
+1
());
-Р /- -
(т)аЧт)-аЧ2
-т);
-т);
п-(
1,
)
сигналов по формулам
А (m,k)A (m,k)+A ( -m,k) + +2А ( -t-m,k)- cosK.(2k-H)/2 ;
(2.k)A ( ,k)4+2A ( ,k) cos УГ (2k+1) /2 ; A. (m,2 -k-1)A (m,k) + +A ( Hn,k)-2/ (2 +m,k)- x-cos-Jt (2k+1)
A(2 - 2 - - -k-1))--2 /(,k) cos (2k-H)/2
.
и определяет значение сигналов Ay(i,k) и A,(i,2 ) в формулах (19) и (20).
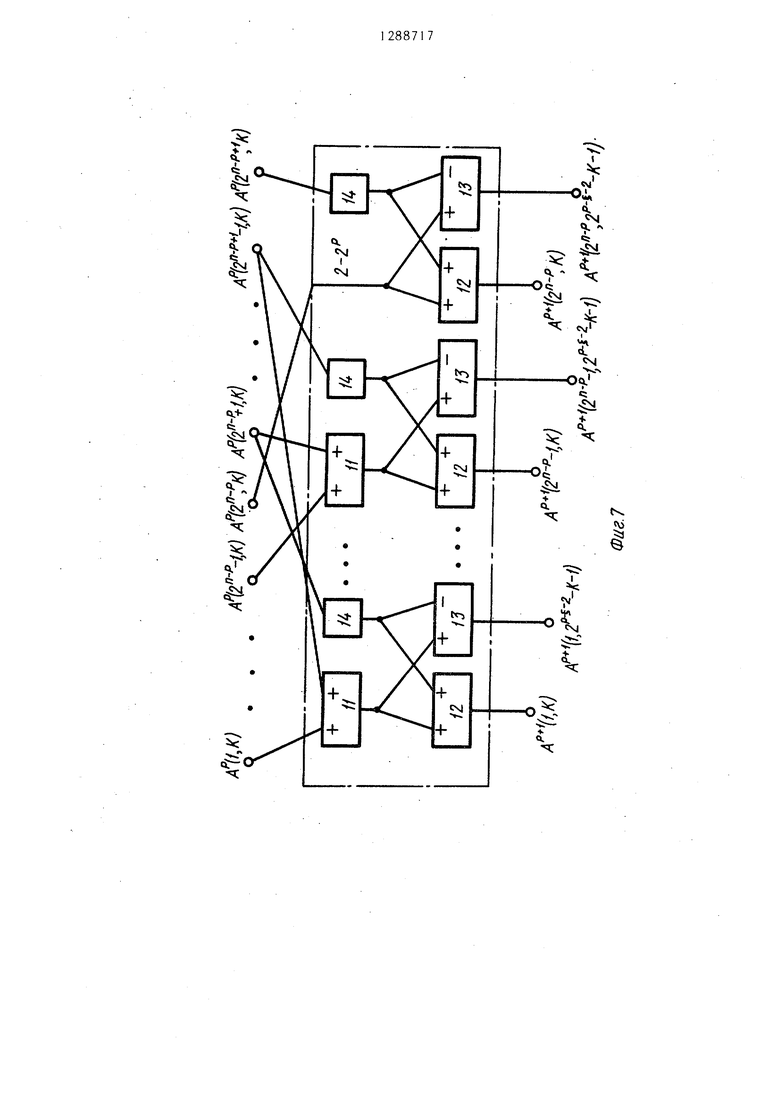
Блок 4 умножения первого рода (фиг. 8) состоит из умножителя 15 с весом ( sinjr (2k+1) для .косинусного канала устройства и с весом sin.li (2k+1) для синусного канала устройства, предназначен для формирования сигналов по формулам: для косинусного канала
15
го-1,2,...,2
и определяет значение сигналов b(i) 20 а,, (i) в формулах (16) и (17).
Блок 2-2 умножения второго рода (фиг. 7) состоит из группы (2 -1) и двух групп по 2 (двухвходовых алгебраических) сумматоров 11-13 и группы 2 умножителей 14 с весом 2 cos ir(2k-H) . Блок 2-2 умножения второго рода предназначен для формирования двух групп сигна.- лов из входной последовательности
25
1288717 -6
F (k) (-1) A (1,k) sinIT(2k+1)/l -«;- для синусного канала устройства F4k)A(1,k) sin3t(2k+1) ;
и определяет значения сигналов F42(k+1)l и FЧ2(2k+1)iи, следовательно , s в формулах (9), (15) и (22).
Из анализа схем (фиг. 1 и 2) видно, что число выходов устройства, а следовательно, и сигналов F (R),F(R) определяется числом блоков 4 умножения первого, рода плюс три (нулевой, ( )-й, (2 )-й сигналы, формируемые блоками 1 -2 сум1 рования второго рода) и равно
К (2 -1) +1; R( -1) 2-И 2 - -1.
Остальные сигналы формируются без увеличения сложности схемьг с учетом равенств (2).
Формула изобретения
Устройство для дискретного преобразования Фурье сигналов, содержащее группу из п блоков суммирования второго рода ( N, N - размер преобразования) , вторая группа выходов р-го (,п) блока суммирования второго рода подключена соответственно к группе входов (р+1)-го блока суммирования второго рода, а первьш и второй выходы группы выходов п-го блока суммирования второго рода являются соответственно (2 )-м и нулевым информационными выходами устройства, отличающееся тем, что, с целью упрощения устройства, оно содержит косинусный и синусньй каналы, каждый из которых содержит блок суммирования первого рода, блок суммирования второго рода, группу блоков умножения первого рода, группу блоков умножения второго рода и группу блоков суммирования второго рода, причем входы блока суммирования первого рода являются группой информационных входов устройства, а выходы блока суммирования первого рода подключены соответственно к входам блока суммирования второго рода, входы i-ro (i ,3,n) блока умножения второго рода
30
35
40
45
50
55
71
подключены к соответствующим выхода первой группы выходов (i-l)-ro блока суммирования второго рода, первая и вторая группы выходов i-гб блока умножения второго рода подклю чены к входам двух (i+1)-x блоков умножения второго рода, а выход п-го блока умножения второго рода подключен к входу блока умножения первого рода, выходы блоков умно- женин первого рода являются, группой информационных выходов устройства, причем блок суммирования первого рода содержит (2 -1) сумматоров, первый и второй входы т-го (т 1,2 -1) сумматора являются соответственно т-м и ()-м входами блока суммирования первого рода, а
i выход ш-го сумматора является т-м выходом блока суммирования первого рода, при этом j-й (,n) блок суммирования второго рода косинусного канала содержит две группы сум маторов, первые входы т-х (, сумматоров первой и второй групп; объединены и являются ( -tn)-M входом блока суммирования второго рода, вторые входы сумматоров первой и второй групп объединены и являются ( +1п)-м входом блока суммирования второго рода, а выходы т-х сумматоров первой и второй групп являются соответственно т-м выходом первой и ( -т)-м выходом второй групп выходов блока суммирования второго рода, причем j-й блок суммирования второго рода синусного канала содержит две
группы сумматоров,первые входыk-x (k 1, -1) сумматоров первой и вто
5
5
0
0
5
0
78
рой групп объединены и являются k-M входом блока суммирования второго рода синусного канала, вторые входы k-x сумматоров первой и второй групп объединены и являются ( -k)-M входом блока суммирования второго рода синусного канала, а выходы k-x сумматоров первой и второй групп являются k-ми выходами соответственно первой и второй групп выходов блока суммирования второго рода синусного канала, при этом.1-й блок умнбжения второго рода содержит три группы сумматоров и группу умножи- телей, первый и второй входы 1-го (,2 -1) сумматора первой группы являются соответственно 1-м и ( -1)-м входами блока умно- жения второго рода, вход s-ro (s 1, ) умножителя группы является ( +s)-M входом блока умножения второго.рода, выход s-ro умножителя подключен к первым входам S-X сумматоров второй и третьей групп вторые входы т-х сз мматоров в.торой и третьей групп являются ( )-м входом блока умножения второго и подключены к выходу k-ro суммато- ра первой группы,1 а выходы т-х (т 1, ) сумматоров второй и третьей групп,являются т-ми выходами соответственно первой и второй групп выходов блока умножения JBToporo рода, блок умножения первого рода косинусного канала выполнен в виде умножителя на (-1) sin il(2k+1) (k 0, ), а блок умножения первого рода синусного канала выполнен в виде умножителя на sin J(2k+1)/2 1
т.тт


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для дискретного преобразования Фурье | 1985 |
|
SU1287174A1 |
| Устройство для определения амплитуды и мощности спектральных составляющих комплексного сигнала | 1985 |
|
SU1309037A1 |
| Устройство для дискретного преобразования Фурье действительной последовательности сигналов | 1986 |
|
SU1357974A1 |
| Цифровой анализатор спектра | 1985 |
|
SU1256044A1 |
| СПОСОБ ПЕРЕДАЧИ И ПРИЕМА СИГНАЛОВ КВАДРАТУРНОЙ АМПЛИТУДНОЙ МОДУЛЯЦИИ, СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ, МАШИНОЧИТАЕМЫЙ НОСИТЕЛЬ И ПРИМЕНЕНИЕ СПОСОБА ДЛЯ СИНХРОНИЗАЦИИ ПРИЕМА СИГНАЛОВ КВАДРАТУРНОЙ АМПЛИТУДНОЙ МОДУЛЯЦИИ | 2005 |
|
RU2286025C1 |
| СПОСОБЫ И УСТРОЙСТВА ПОВЫШЕНИЯ ИНДЕКСА УГЛОВОЙ МОДУЛЯЦИИ | 2012 |
|
RU2493646C2 |
| Усреднитель-анализатор спектра Фурье | 1980 |
|
SU955086A1 |
| Устройство для вычисления коэффициентов фурье | 1977 |
|
SU645163A1 |
| УСТРОЙСТВО ОЦЕНКИ ЧАСТОТЫ ГАРМОНИЧЕСКОГО ЗАШУМЛЁННОГО СИГНАЛА | 2016 |
|
RU2643708C2 |
| БЫСТРОДЕЙСТВУЮЩИЙ МНОГОФУНКЦИОНАЛЬНЫЙ ПРЕОБРАЗОВАТЕЛЬ УГЛА В КОД ДЛЯ УСТРОЙСТВ ЭЛЕКТРОМЕХАНОТРОНИКИ | 1994 |
|
RU2094945C1 |
Изобретение относится к обл-асти автоматики и вычислительной техники, в частности к устройствам дискретного преобразования Фурье сигналов, и может найти применение при построении параллельных спектральных анализаторов . Цель изобретения - упрощение устройства. Поставленная цель достигается за счет того, что устройство содержит группу из п блоков суммирования второго рода, косинусный и си- нусньй каналы, каждый из которых состоит КЗ блока суммирования первого рода, блока суммирования второго рода, группы блоков умножения первого рода, группы блоков умножения второго рода и группы блоков суммирования второго рода. 8 ил. (Л 1ЧЭ 00 00 
4 I
F(i)
)()
Ouz-i
/.-2
fii )
х(о) т ш} ( 4 )(() () ) /()
а(о)
о
а(1)
т Л(/; Х(2)) ) ) )( )()
Фиг.З
а) а () )
Г(2)
Фиг.У
6 )
)
о. 0.
«5
4:
.
г
N
00.
с:
J
ч:
tv
-i
t:
cvj
о.
+
4- с.
ч:
п
)
ff
6W Фиг 8
П
,J

| Способ определения наличия и местоположения неоднородностей в линии передачи электромагнитной волны СВЧ диапазона и устройство для его осуществления | 1981 |
|
SU1084707A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Шафоростов Ю.И | |||
| Новая схема алгоритма быстрого преобразования Фурье: В сб | |||
| Автоматизированные моделирующие системы в технологических задачах | |||
| Куйбьшев, 1984, с.55- 61. | |||
Авторы
Даты
1987-02-07—Публикация
1985-08-01—Подача