В известных аналоговых вычислительных устройствах для воспроизведения функций одной или двух переменных, заданных в виде гра411коБ или таблиц, применяются диодные функциональные преобразователи, построенные на способе суммирования ломаных отрезков, или используется представление функции двух переменных функциями одной переменной. Однако существующие способы построения функциональных преобразователей не позволяют непосредственно и независимо настраивать и изменять апликаты функции, что ограничивает об.гасть применения этих способов.
Предлагаемый способ воспроизведения функций одной или двух переменных, основанный на кусочной аппроксимации, позволяет строить функциональные преобразователи для щирокого класса функций и увеличивать точность их воспроизведения, для чего функцию образуют из ряда элементарных функций (линий, поверхностей) и максимальную или минимальную из них выделяют применением логических схем «ИЛИ и «И. На входы этих схем подаются напряжения, изменяющиеся непрерывно, а на выходе появ.г яются напряжения, которые равны наибольшему или наименьщему из входных напряжений.
Устройство для осуществлеиия предлагаемого способа отличается от известных тем, что для воспроизведения треугольной функции от каждой из двух входных переменных оно содержит функциональные преобразователи, по матричной схеме подключенные к блокам умножения, а выходы последних подсоединены к сумматору.
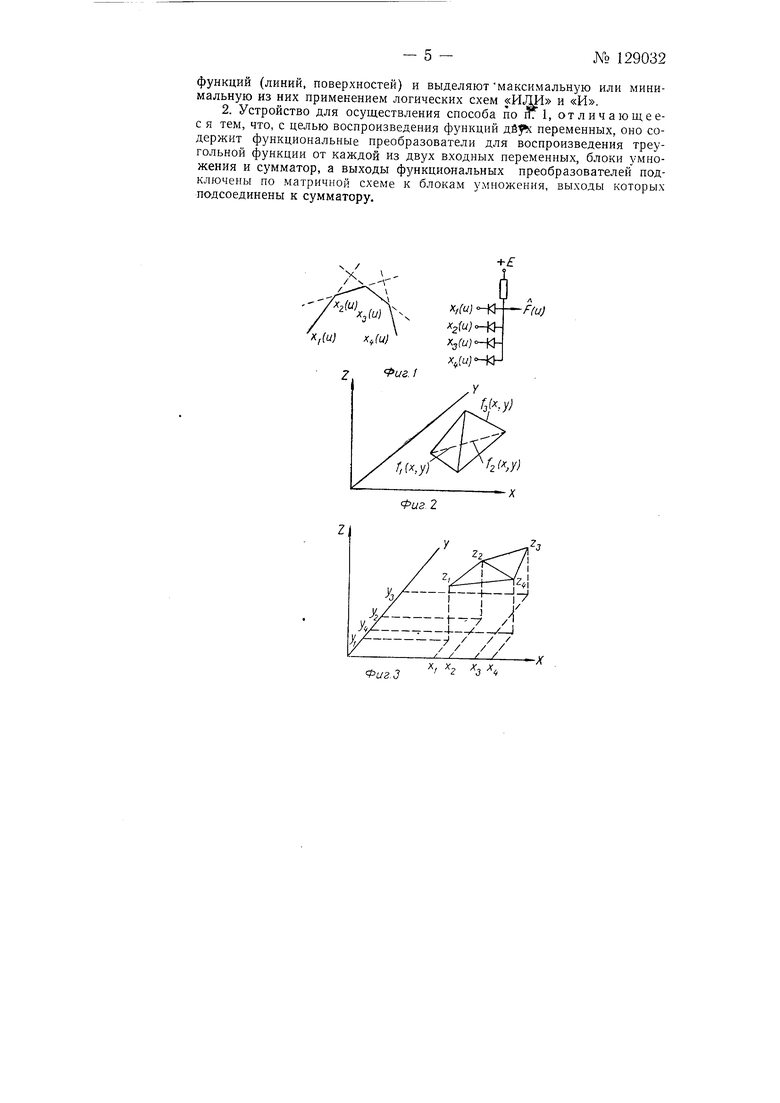
Рассмотрим возможность изображения заданной нелинейной функции одной непрерывной переменной (u) путем ее логического построения из ряда элементарных функций х,(и), у (и) . . . z(u) (в дальнейщем для простоты будем считать их линейными). Кривые, удовлетворяющие условию F (и) О или условию F (и) О могут быть аппроксимированы касательными прямыми соответственно следующим образом:№ щ F 129032- 2 ) OrflSeeM /(ы)-макс yi(«X 2(«) Уn(), ; при fCwj О,преем/(«)-мин A-i(wX JCJ(M:) . л:„(м). ри®|м следу о.щее сокращенное обозначение этих функций: .,;-.«)г-о («); /(V.) Пример построения функции вида Г{и) показан на фиг. 1. Кривые с несколькими экстремумами можно синтезировать с помощью указанных функций и вспомогательной кривой А(и), приходяей через точки F(u)0. Например, если кривая обладает тремя максимумами и двумя минимумами, то она может быть логически выражена следующим обраом: (M) - мин { макс FI(II}, F(u), Р,(ч, A(tt}, Д(и), F.(ii)} макс { мин I/,r«), ЛД«), А(и, А(«). F,(ii F,(u). Таким же образом можно логически образовать функцию с любым числом экстремумов. Ниже рассматривается возможность изображения заданной функции двух переменных (x,y) путем ее логического построения из ряда элементарных функций двух переменных f(x,y); f2(x,y); fz(x, у)В простейшем случае будем считать, что эти элементарные ф нкции являются линейными, то есть f(x,y) 2(х,у)а х+Ь2У+С; /з(л;,.г/)азЛ+ зУ+С и геометрически представляются в виде плоскостей. Путем выполнения логических операций между такими элементарными плоскостями можно осуществить кусочно-плоскостную аппроксимацию заданной поверхности. В качестве примера на фиг. 2 приведена поверхность в виде пирамиды, стоящей на плоскости х, у. Если каждая из боковых граней этой пирамиды выражается функциями fi(x,y); f2(x,y); fz(x,y), то вся поверхность в целом в логической форме выражается: Р(х,у) макс{тп1 fiX,y), ,у), f.(x,y 0. В общем случае, когда функция двух переменных задана в виде некоторого числа точек в пространстве х, у, z к необходимо построить кусочно-плоскостную аппроксимацию заданной поверхности, то это может быть выполнено путем соединения этих точек. В результате будут образованы треугольники (фиг. 3). Если теперь между образованными плоскостями выполнить логические операции «макс и «мин, то получится граненая поверхность, аппроксимирующая заданную функцию двух переменных. Сказанное выше выявляет преимущество предлагаемого способа перед известным методом суммирования для случая немонотонных функций. Значительная часть таких кривых при методе суммирования образуется как малая разность больших величии, что может приводить к неустойчивой работе схемы. При использовании предлагаемого способа разности не образуется, так как каждая точка результирующей кривой создается самостоятельно (образуется только одной из элементарных функций). Ниже описывается вариант построения устройства, реализующего предлагаемый способ воспроизведения функций двух переменных, в котором непосредственно задаются апликаты Zi, Т., Z, . . . . При этом интервалы х и &у между заданными абсциссами и ординатами постоянны.
Интерполяция осуществляется следующим образом. Текущее значение Z внутри четырехугольника с апликатами Zi,j; Zi, .ц.у; Z,+ i,y+i определяется как взвещенная сумма заданных апликат. При этом вес пропорционален произведению текущих координат х и у от заданной апликаты, диаметральной по отнощению к взвещиваемой.
Таким образом
,,) (/-3,.)-f 2/,у + , (/-«J Ру (+ьу«/ (1-8у) +Z,+ b,4, а, (1)
Такая интерполяция приводит к необходимости образования функций а, р, 1-а, 1--р и суммы произведений этих функций.
Рассмотрение перехода от одного интервала к другому показывает, что указанные функции должны быть «треугольными, то есть линейно возрастающими в предществующем интервале, линейно убывающими в последующем интервале и равными нулю во всех остальных интервалах.
Обозначим эти треугольные функции -(х) и Х (у). Общую формулу для аппроксимации двух переменных при заданных апликатах можно записать в следующей форме:
/ j П
Z-. S Z,/.,-,()X,.-,(y)--Z,,,.-.,X,.-,(A-)X;)-Z,+,,/,(x)A,..,()-f (2) -}-Zi+,j+,x)lj(y).
При любых значениях хну все члены этой суммы, за исключением четырех, для которых 0, обращаются в нуаь. Оставшиеся четыре члена образуют интерполяционную формулу (1).
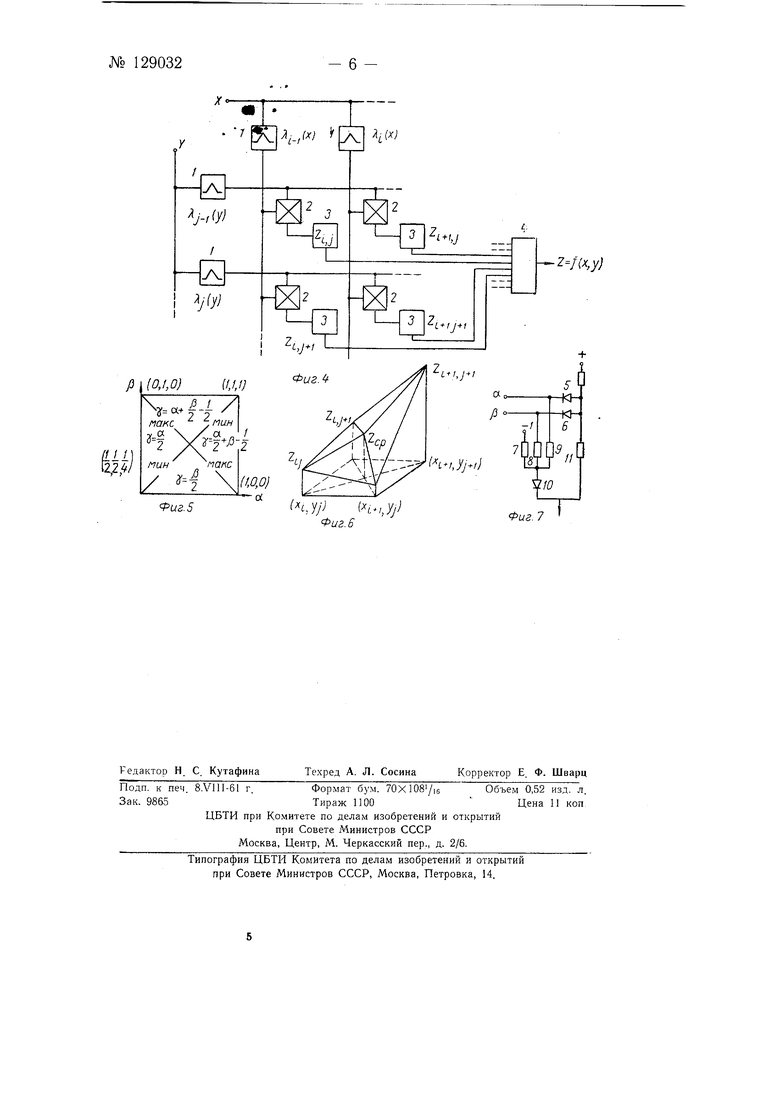
На фиг. 4 показана структурная схема моделирования интерполяционной формулы.
На схеме: / - функциональные преобразователи для воспроизведения треугольных функций; 2-блоки умножения; 3-элементы для задания апликат и 4-сумматор. Выходы функциональных преобразователей подключены по матричной схеме к блокам умножения, а выходы последних - к сумматору.
Если заданы апликаты функции для т абсцисс х и п ординат yjто все устройство для аппроксимации функции двух переменных потребует: п+т треугольных функций, т-п блоков умножения двух переменных, столько же элементов для задания апликат и один сумматор.
Электрические схемы для получения треугольных функций могут строиться на логической основе, как показано выще.
С целью уменьщения числа схем умножения осуществляется кусочно-плоскостная аппроксимация функции путем применения логических операций выбора максимальной или минимальной из двух величин.
Поставим себе задачу осуществить кусочно-плоскостную аппроксимацию функций двух переменных.
Следовательно, интерполяция между четырьмя апликатами
Zij,- Zi+i,j; Zi,j+ и Z,i-i,,-+i также должна быть кусочно-плоскостной. Пусть, как и в случае интерполяционной формулы (1), апликата для
центра четырехугольника Xcp - -i Xi.); (yi-yj+i) есть
средне-арифметическая апликат его верщин, то есть
- 3 -№ 129032
О.Гоу
где ,. Дл- - ,
№ 129032 - 4 1У + 1 (-М ; + l
Кусочно-плоскостная интерполяция получается путем соединения прямыми линиями точки 2, с точками Z,,у Z;,y+/,. 4+лу и ,,+, В целом кусочно-плоскостная аппроксимация функции двух переменных в данном случае образуется в виде граненой поверхности, причем каждая грань представляет собой плоский треугольник, две из вершин которого определяются смежными заданными координатами, а третья - средней координатой.
Кусочно-плоскостная аппроксимация заданной функции может быть получена путем замены в интерполяционной формуле (1) функций а, (1-а)р., (1-р)аи (1-а)(1-j3) на кусочно-плоскостные аппроксимации этих функций. При умножении двух переменных функция изображается поверхностью 2-го порядка. Рассмотрим аппроксимацию такой функции граненой поверхностью в пределах изменения переменных О а 1. О : р 1 и при условии, что в точках , (
. Р -- ; , аппроксимирующая поверхность совпадает
со значениями функции 7 аРНа фиг. 5 показаны координаты совпадающих точек, уравнения граней аппроксимирующей поверхности и ее вид в плане. На ребрах граненой поверхности показано, какие логические операции (макс или мин) должны быть выполнены между двумя соседними гранями.
Можно показать, что уравнение аппроксимирующей поверхности может быть выражено в следующей форме
. 5 J I мип(а.) + макс а-|-3-/), 0 I(-3)
Обозначая приближенное умножение по формуле (3) через Я(а,р) и подставляя его в интерполяционную формулу (1), получим следующее выражение для кусочно-плоскостной интерполяции.
Z Z,,/7tX,i(;),,.i(y)-fZi,,.,-i(-c), XXy)-rZ;+„,.).,.,(у) f
г2,н-ь;+,Я),ХлХ v(y)j
Это выражение изображается поверхностью, изображенной на фиг. 6.
При кусочно-плоскостной аппроксимации функции двух переменных структурная схема, приведенная на фиг. 4, остается прежней, по устройства умножения приобретают другое содержание.
Электрическая схема «умножения по формуле (3) показана на фиг. 7. С помощью диодов 5 к 6 выполняется операция выбора минимального из двух напряжений аир. Сопротивления 7, 8 vi 9 служат дли образования суммы а+р-1. Диод W служит для сравнения этой суммы с нулем. Сопротивление 11 используется для суммирования результатов двух логических операций.
Независимые переменные вводятся в устройство в виде напряжений постоянного тока. Изображаемая функция получается на выходе устройства также в виде напряжения постоянного тока.
Предмет изобретения
1. Способ воспроизведения функций одной или двух переменных, основанный на кусочной аппроксимации, отличающийся тем, что, с целью расщирения класса воспроизводимых функций и увеличения точности их воспроизведения, функцию образуют из ряда элементарных
функций (линий, поверхностей) и выделяютмаксимальную или минимальную из них применением логических схем «ИДИ и «И.
2. Устройство для осуществления способа по гГ1, отличающеес я тем, что, с целью воспроизведения функций переменных, оно содержит функциональные преобразователи для воспроизведения треугольной функции от каждой из двух входных переменных, блоки умножения и сумматор, а выходы функциональных преобразователей подключены по матричной схеме к блокам умножения, выходы которых подсоединены к сумматору.
- 5 -№ 129032



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для построения математических функций | 1959 |
|
SU125051A1 |
| Интерполятор | 1984 |
|
SU1206805A1 |
| Устройство для воспроизведенияфуНКций дВуХ пЕРЕМЕННыХ | 1979 |
|
SU842850A1 |
| Устройство для воспроизведения функций двух переменных | 1977 |
|
SU742972A1 |
| Устройство для воспроизведения функций двух переменных | 1980 |
|
SU905827A1 |
| Электрическое устройство для изображения функции двух переменных | 1960 |
|
SU134458A1 |
| Устройство для воспроизведения функций двух переменных | 1982 |
|
SU1073783A1 |
| Генератор функций | 1984 |
|
SU1275411A1 |
| Гибридный функциональный преобразователь | 1988 |
|
SU1524072A1 |
| Устройство для воспроизведения функций двух переменных | 1976 |
|
SU637827A1 |

+
XfW (uj V Hcb XjfwjHCh x.fwj-WЫ У)
Фиг.
10,/,0)
4-1-2 / ff/KC у I ... a /a „ / 2
папе
у
а-2
ИДО) и
(jy; (i.i,yj)
иг.5
Фиг. 6
,y;
Ln,
3 t-/JyW
Фиг. 7

Авторы
Даты
1960-01-01—Публикация
1959-07-17—Подача