1
(21)4397391/24-24
(22)25.03.88
(46) 23,11.89. Бюл, № 43
(71)Московский авиационный институт им. Серго Орджоникидзе
(72)О.Н.Сахаров и М.И.Чебатко (53) 681.335(088.8)
(56)Авторское свидетельство СССР № 385291, кл. G 06 G 7/26, 1971.
Блок БНА-3. Техническое описание и инструкция по эксплуатации. ПТЗ 073.036-OS ТО, НИИСЧЕТМАШ, 1982. .(54) ГИБРИДНЫЙ ФУНКЦИОНАЛЬНЫЙ ПРЕОБРАЗОВАТЕЛЬ
(57)Изобретение относится к аналоговой и аналого-цифровой (гибридной) вычислительной технике и может применяться при моделировании систем автоматического управления. Целью иэоб- ретения является повышение точности. Гибридный функциональный преобразователь содержит блок 1 преобразования аргумента, блок адресации 3, блок 4 памяти коэффициентов интерполяции, умножающие цифроаналоговые преобразователи 5-10, сумматоры 11-13, блоки умножения 14, 15. В гибридном функциональном преобразователе используется метод кусочно-квадратичной интерполяции заданной функции, причем на каждом участке интерполяции заданная функция определяется как средневзвешенная сумма двух квадратичных полиномов. Это позволяет не только повысить точность воспроизведения функции, но и ее гладкость. 2 ил.
,


| название | год | авторы | номер документа |
|---|---|---|---|
| Гибридный функциональный преобразователь | 1988 |
|
SU1603405A1 |
| Гибридное устройство для воспроизведения функций | 1986 |
|
SU1319049A1 |
| Функциональный преобразователь | 1989 |
|
SU1619321A1 |
| Функциональный декодирующий преобразователь | 1976 |
|
SU696489A1 |
| Устройство для воспроизведения функций двух переменных | 1984 |
|
SU1265805A1 |
| Функциональный преобразователь нескольких переменных | 1986 |
|
SU1387022A1 |
| Устройство для воспроизведения функций двух переменных | 1987 |
|
SU1517046A1 |
| Гибридный функциональный цифроаналоговый преобразователь со сплайновой аппроксимацией n-го порядка | 2016 |
|
RU2628918C1 |
| Функциональный преобразователь | 1985 |
|
SU1304040A1 |
| Устройство для воспроизведения функций двух переменных | 1986 |
|
SU1343428A1 |
Изобретение относится к аналоговой и аналого-цифровой (гибридной) вычислительной технике и может применяться при моделировании систем автоматического управления. Целью изобретения является повышение точности. Гибридный функциональный преобразователь содержит блок 1 преобразования аргумента, блок адресации 3, блок 4 памяти коэффициентов интерполяции, умножающие цифроаналоговые преобразователи 5-10, сумматоры 11-13, блоки умножения 14,15. В гибридном функциональном преобразователе используется метод кусочно-квадратичной интерполяции заданной функции, причем на каждом участке интерполяции заданная функция определяется как средневзвешенная сумма двух квадратичных полиномов. Это позволяет не только повысить точность воспроизведения функции, но и ее гладкость. 2 ил.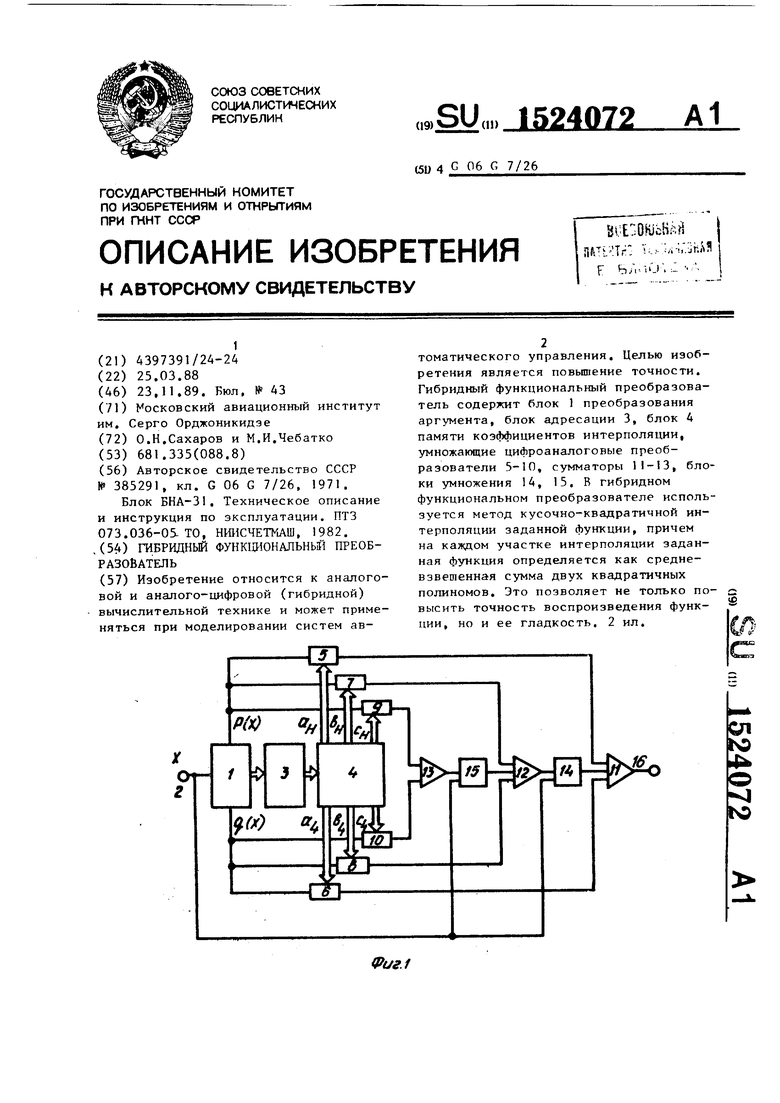
Изобретение относится к аналоговой и аналого-цифровой (гибридной) вычислительной технике и может быть применено, в частности, при моделировании систем автоматического управления ,
Целью Изобретения является повышение точности.
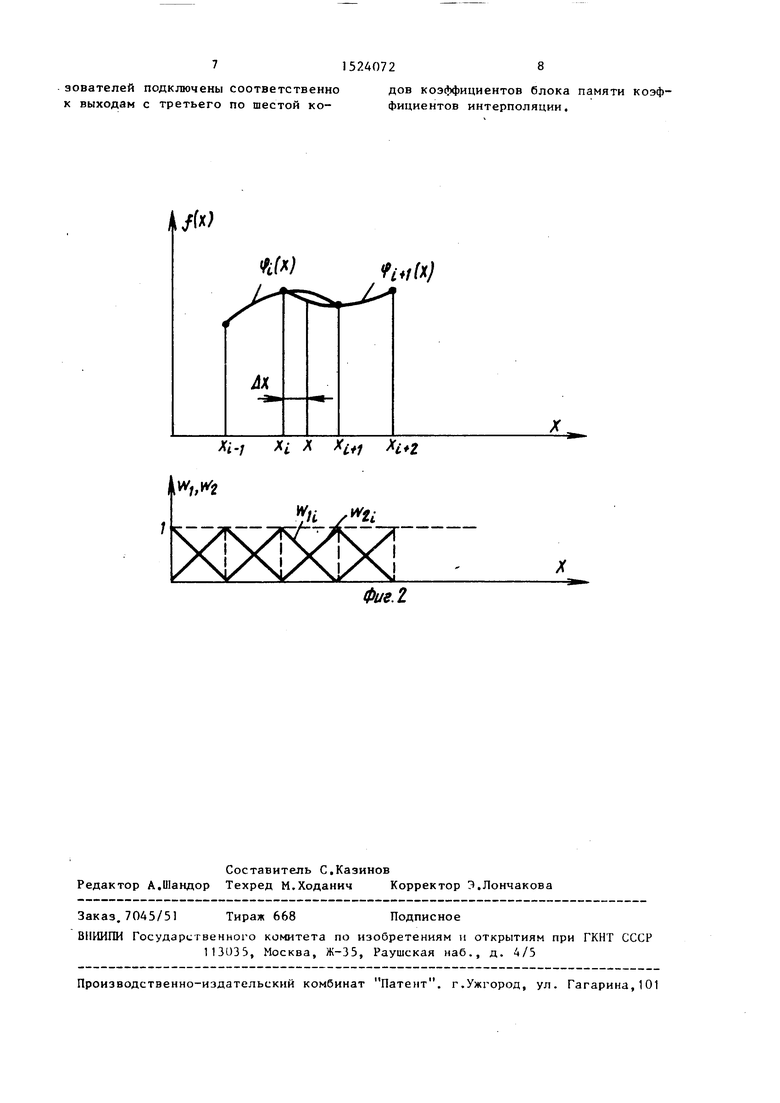
На фиг.1 представлена структурная схема предлагаемого гибридного Лунк- ционального преобразователя; на фиг, 2 - пример интерполяции функции одной переменной на i-M интервале интерполяции «
Гибридный функциональный преобразователь содержит блок 1 преобразования аргумента, вход 2 гибридного функционального преобразователя, блок 3 адре .сации, блок 4 памяти коэффициентов интерполяции, первый 5, второй 6, третий 7, четвертый 8, пятый 9 и шестой 10 умножающие цифро-аналоговые преобразователи, первый 11, второй 12, третий 13 сумматоры, первый 14 и второй 15 блоки умножения и выход 16 гибридного функционального преобразователя.
Устройство работает следующим образом.
Заданная функция f(x) может буть представлена аналитическим выражением или совокупностью дискретных значений f(x;), где ,I|,.,,n - номер точки разбиения по оси х. Закон разбиения оси аргумента равномерный с шагом h. Для каждой точки разбиения строится квадратичный полином (фиг.2) проходящий через опорную точку f(x|) и две соседние с ней точки.
I .
На 1-м участке интерполяции для
любого , х;., заданная функци f(x) определяется как средневзвешенная величина двух квадратичных поли -
номов
f(x) q.,(x).w,; -H Cfi,,(x)-w,; (1)
где L (х) - полином, проведенный черкез точки f(x,-, ), f(x;), f(x;,, );
Ч Jti полином, проведенный через точки f(x),
f (х;, ), f (х, +2 )J весовые коэффициенты.
Полиномы ср; (х) и , (х) опреде ляются следующими выражениями:
Ср;(х) а, + bi X -I- с; , (х) а ; + , + Ъ U, X +с;, х.
где а;, Ь; ,
1 +
, h ; 1 , с j.« - постоянные коэффициенты полиномов -tf; (х) и Lf;4( (х), которые рассчитьшаются при предварительной подготовке функции.
Весовые коэффициенты W и Wg; определяются выражениями:
Т7 1
W,; 1 - ---,
W,
Лх
где Лх х-Х ,
Таким образом, весовые коэффициенты на всем диапазоне изменения переменной X представляют собой треугольные функции (фиг,2), т.е. прямое и противофазное ему приращения аргумента
р(х)
1, при , о, при ,
q(x) ° Р I 1 , при ,
где Хц и Хц - точки разбиения оси х с четными и нечетными номерами.
Для удобства адресации введено понятие четных и нечетных полиномов Ц ц и , проведенных через соответствующие опорные точки х ц и Хц
Cf ац + с„. х, (ц а +Ьц X + Сц. X ,
где а ц, Ъц, Сц - коэффициенты полинома
а ц, Ьц, с - коэффициенты полинома If ц .
Тогда интерполяционное выражение (1) можно записать в виде
f(x) а. р(х)+ау. q(x) + + Ьц-р(х)(хТ+ с.ц. р(х) + + Сц q(x) х х,(2)
На этапе подготовки функционального преобразователя к работе дискретные значения коэффициентов интерполяции записываются в блок 4, который имеет две зоны. В первую зону блока 4 записываются значения а, Ь,, с при i-нечетных, а во вторую зону - значения а , Ь;, при i-чет- ных.
Для воспроизведения функции напряжение, соответствующее входной переменной, подается на вход блока 1 преобразования аргумента, который выра51
батывает двоичный код номера интервала разбиения, т.е. код узлового значения аргумента. В соответствии с этим кодом блок 3 адресации для каждого i-ro интервала вырабатывает два адреса А ц и
Ч
Блок 4 функционального преобразовтеля должен содержать три однотипных блоиа памяти. Каждый из указанных блоков хранит дискретные значени
и
в
в другой
одной зо- зоне, причем их адресные шины соответственно объединены и подключены к выходам блока адресации.
По адресу А ц из первой зоны первого блока памяти считывается код, соответствующий коэффициенту а, из первой зоны второго блока - Ъц, из первой зоны третьего блока - с. Аналогично производится считывание по адресу А(,.
На цифровые входы преобразователей 5, 7 и 9 подаются коды, соответствующие ац, Ъ, с ц а на аналоговые входы - напряжение, соответствующее функции р(х), с прямого выхода блока 1. Аналогично, на цифровые входы преобразователей 6, 8 и 10 подаются коды, соответствующие ац, Ь, и Сц, а на. аналоговые входы - напряжение, соответствующее функции q(x).
Напряжение на выходе сумматора 13 соответствует выражению (х) -
Ci,-q(x), напряжение на выходе блока 15 - выражению р(х)+Сц q(x)J х. Сумматор 12 реализует cyMMv Ь,, р(х) + +Ьц-q(x) + (x)-t-Cj. q(x) , а блок 14 умножает напряжение, соответствующее значению этой суммы на напряжение, соответствующее переменной х.
Напряжение на выходе сумматора 11, соответствующее текущему значению функции, определяемой в соответствии с интерполяционным выражением (2), является выходным напряжением гибридного функционального преобразователя.
Предлагаемый гибридный функциональный преобразователь обеспечивает по- вышение точности до 30% и гладкости воспроизведения функции за счет интерполяции ее средневзвешенной суммой двух квадратичных полиномов.
Формула изобретения
Гибридный функциональный преобразователь, содержащий блок преобразования аргумента, подключенный входом к входу гибридного функционального преобразователя, прямым выходом приращения аргумента - к аналоговому входу первого умножающего цифроаналогового
преобразователя, противофазным выходом приращения аргумента - к аналоговому входу второго умножающего циф0 роаналогового преобразователя, а выходом кода узловых значений аргумента - к входу блока адресации, соединенного выходом с входом блока памяти коэффициентов интерполяции, выходы
5 первого и второго кодов коэффициентов которого подключены к цифровым входам соответственно первого и второго умножающих цифроаналоговых преобразователей, выходы которых сое0 динень соответственно с первым и вторым входами первого сумматора, выход которого является выходом гибридного функционального преобразователя
отличающийся тем, что, с целью повышения точности, в него введены два блока умножения, второй и третий сумматоры и с третьего по щес- той умножающие цифроаналоговые преобразователи, причем первый блок умножения подключен выходом к третьему входу первого сумматора, входом первого сомножителя - к входу гибридного функционального преобразователя и входу первого сомножителя второго
5 блока умножения, а входом второго сомножителя - к выходу второго сумматора, соединенного первым и вторым входами с выходами третьего и четвертого умножающих цифроаналоговых
0 преобразователей соответственно,
а третьим входом - с выходом второго блока умножения, подключенного входом
5
0
второго сомножителя к выходу третьего сумматора, первый и второй входы которого соединены с выходами пятого и шестого умножаюш 1Х цифроаналоговых преобразователей соответственно, причем аналоговые входы третьего и пятого умножающих цифроаналоговых преобразователей подключены к прямому выходу приращения аргумента блока преобразования аргумента, соединенного противофазным выходом приращения аргумента с аналоговыми входами четвертого и шестого цифроаналоговых преобразователей, а цифровые входы с третьего по тестой умножающих цифроаналоговых преобраэователей подключены соответственно дов коэффициентов блока памяти коэф- к выходам с третьего по шестой ко- фициентов интерполяции.
U()
Xi-j )(i л
% ti
Фиг. г

Авторы
Даты
1989-11-23—Публикация
1988-03-25—Подача