jffue.f
Изобретение относится к вычислительной технике и может быть использован в системах диагностирования в качестве источника входных воздействий.
Цел изобретения - увеличение периода формируемых последовательностей.
На фиг.1 приведена схема генератора; на фиг.2 - 4 - примеры реализации преобразователя кодов.
Устройство содер;кит счетчик 1 , преобразователь 2 кодов, блоки 3 умножения, блок 4 сложения, блок 5 деления и регистры 6.
На фиг.1 показан также тактовый вход 7 устройства.
Устройство работает следующим образом.
Перед началом работы все регистры 6 и счетчик 1 устанавливаются в нулевое состояние„ Регистры 6 уста
навливаютс,я в одном из разрешенных состояний. Запрещенными являются, например, состояния L,(L+1),...,
иЗеоыС ,.
(2 - 1) какого-либо из регистров 6. Установочный вход устройства на фиг.1 не показан.
При О на всех выходах преобразователя 2 устройство работает обычным, образом в соответствии с уравнением
f2(t+l) Q(t)T,
где Q (t+l)Q,(t+l)...Q-(t+l)...
...QnCt+l); 57(t) Q,(t)...
V .Q;(tV. ...Q,(t); Qj(t) и Q;(t+l) - содержимое i-ro регистра, i 1,N, соответственно в моменты времени t и (t+1) (до и после прихода соответствующего тактового импульса), а Т - сопровождающая матрица вида

| название | год | авторы | номер документа |
|---|---|---|---|
| Генератор L-ичных последовательностей | 1986 |
|
SU1406586A1 |
| Счетчик | 1986 |
|
SU1422403A1 |
| Генератор цифровых последовательностей | 1987 |
|
SU1513449A1 |
| Запоминающее устройство с контролем информации | 1984 |
|
SU1288758A1 |
| Устройство для деления многочленов | 1986 |
|
SU1483461A1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2776346C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2023 |
|
RU2815485C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2761766C1 |
| Устройство для контроля | 1984 |
|
SU1265994A1 |
| Генератор псевдослучайных последовательностей | 1986 |
|
SU1406738A1 |
Изобретение относится к вычислительной технике и может использоваться в системах тестового диагностирования в качестве источника входных воздействий. Цель - увеличение периода формируемых последовательностей, что достигается благодаря введению в генератор, содержащий N регистров 6, где N - степень образующего многочлена с коэффициентами из поля GF (L),блок 4 сложения, блок S деления, Р-блоков 3 умножения (Р N) , преобразователь 2 кодов, счетчика 1 с соответствующими связями. Устройство формирует L-ричную последователь-, ность длиной т(Ь - I), где m - длина повторяющегося фрагмента управляющего воздействия. 4 ил. i (Л С
-§i.
So
-§iао
О О ... , О О ... О
Счетчик 1 и преобразователь 2 ко- дов вводятся в состав устройства для формирования на последней группе входов блока 4 сложения периодических управляющих воздействий.
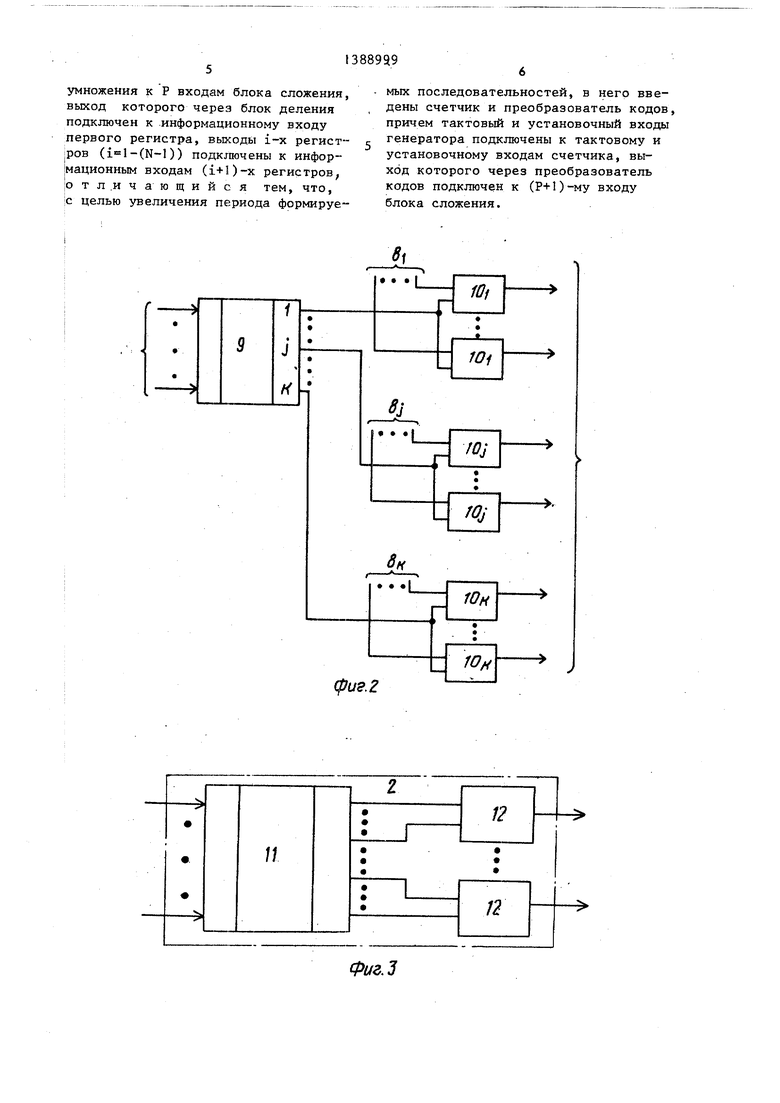
На фиг.2 показана структурная схема преобразователя, формирующего управляющие воздействия произвольного вида, содержащего группы 8. управляющих входов преобразователя, на которых задается код j-ro символа управляющего воздействия, дешифратор 9, элементы И 1 О.
Если в качестве счетчика 1 исполь- зуется, например, трехразрядный счетчик по модулю га 7, а L 5, PCX) - образующий многочлен, примитивный над полем GF (5), период формируемой последовательности становится рав- ньм 8, m (L -I) 7() 168. Для сравнения можно указать, что период пятиричной последовательнос
О ... О
, al а„ GF(L)
0
5
.
5
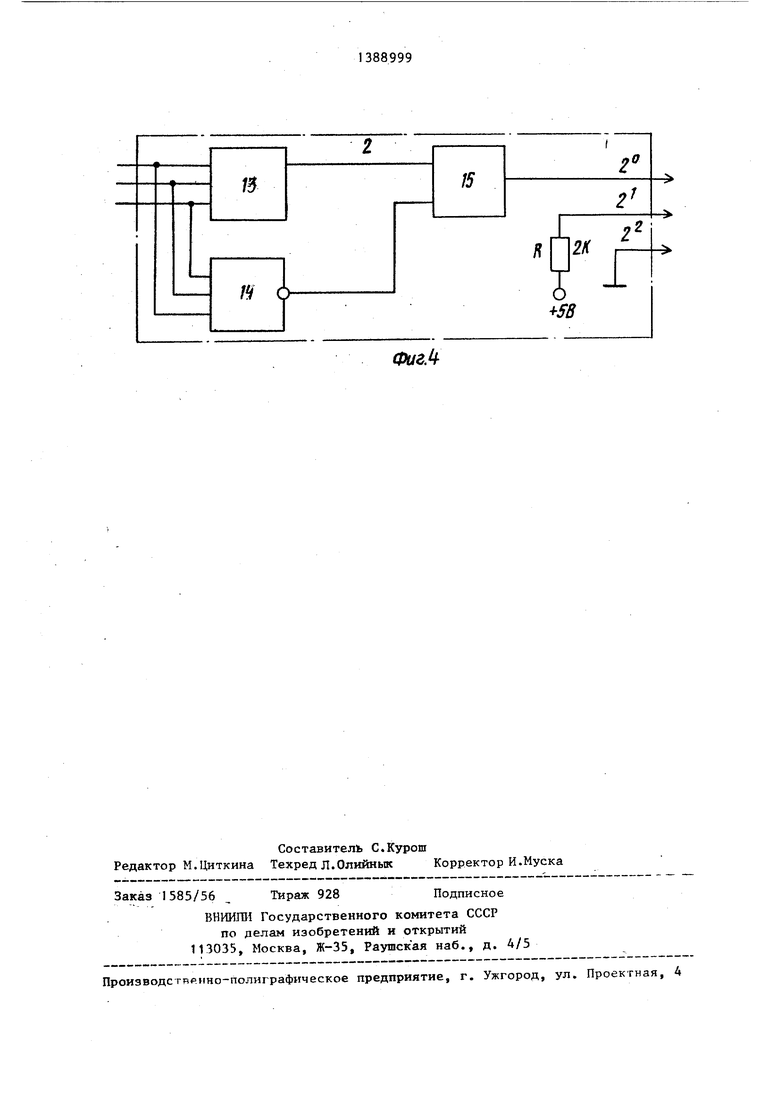
ти, формируемой обычным генератором с таким же количеством последователь- костных злемёнтов (равным 9) , равен лишь S 5- 1 124. С увеличением N разница между Зд и S,, возрастает. Если необходимо сформировать управляющее воздействие определенного вида, то преобразователь 2 имеет вид, показанный на фиг.З, и содержит дешифратор 1 1 и элементы ИЛИ 12, число которых п .
Другой возможный путь - реализация преобразователя 2 на основе ПЗУ, адресные входы которого становятся входами преобразователя, а выходы - вькодами преобразователя. В простейших случаях, при малых m и L, преобразователь 2 кодов можно построить, используя известные методы синтеза комбинационных схем, например, метод диаграмм Вейча.
На фиг.4 показан пример построения преобразователя 2, содержащего дешифратор, который реализован на элементе И 13 и элементе ИЛИ- НЕ 14, элементе ИЛИ 15, формируемое воздействие имеет вид 3222223 (для 3-х разрядного счетчика по модулю 7 и 3).
Рассмотрим периодические свойст- на формируемых последовательностей.
Определение 1.
Последовательность L-ричных чисел поступающих на входы генератора (блоки 3,4,5 и регистры 6), называет ся управляющей последовательностьюAg.
Определение 2.
Повторяющийся фрагмент G управляющей последовательности, где ,Gi.. . .. ,ff ,6-5 GF(L)p 1,m, имеющий минимальную длину m, назьшается элементарным входным воэдействием.
Известно, что устройство, содержащее блоки 3,4,5 и регистры 6, осу- ществл ет деление многочлена последовательностей, поступающих на пселеднюю грзшпу входов блока сложения, на многочлен, инверсный по отношенш к образующему многочлену Ф(X).Не- пользуя это свойство, можно доказать следующие теоремы.
Теорема 1. .
Максимальный период формируемой последовательности равен m(L -1), где N - степень образующего многочлена, примитивного над полем GF(L).
Теорема 2.
Пусть эадан многочлен А(Х) степени п + ft вида
А(Х) 6i,xP( . . .) , Ы-е GF(L), V О, р О - целое.
Ы
Если (n+m) 0(mod(L -I)), то много- член А(Х) делится без остатка на любой многочлен степени N, примитивный над полем GF(L).
Теорема 3. .
Если образующий многочлен Ф(Х) генератора является примитивным над полем GF(L), а н.о.д. ( () ,т) , то формируемая последовательность является последовательностью максимальной длины.
Теорема 4.
Если удовлетворяются условия теоремы 2 И G (X) (где G (X) - многочлен, соответствующий элементарному входному воздействию) делится без остатка на Ф (Х), то нулевое состояние всех регистров генератора одновременно не входит в полное кодовое кольцо децимаций по индексу m состояний генератора.
Теорема 5.
Символы любой формируемой последовательности можно представить в
виде
+ ot; D.d; +... +
m-i ,(0 , -....,D d, ,
гдеоб) е- GF(L);
D - оператор задержки на j тактов ;
d . - i-й элемент последовательности, формируемой под воздействием А , состоящей из фрагментов вида (j
1 О О
0.
ia-1
Таким образом увеличивается период формируемой последовательности до величины ), которая значительно больше периода последовательности, получающейся обычным образом при -Использовании равного количества последовательностных элементов. Следует отметить, что последовательности, формируемые генератором, на входы которого поступают периодические управляющие воздействия, обладают качественно новыми свойствами по сравнению с обычными М-последователь- ностями, которые являются простейшими частными случаями рассмотренных при m 1.
Формула изобретения
Генератор тестовых последовательностей, содержащий N регистров (N - степень образующего многочлена с коэффициентами из поля GF(L)), блок сложения в поле GF(L),блок деления в поле GF(L), Р блоков умножения в поле GF(L) (Р N) ,причем тактовый и установочный входы генератора подключены к тактовым и установочным входам регистров, выходы регистров, соответствующих ненулевым коэффициентам образующего многочлена, подключены через соответствующие блоки
умножения к Р входам блока сложения, выход которого через блок деления подключен к .информационному входу первого регистра, выходы i-x регист- jpoB ((N-l)) подключены к инфор- мационным входам (i.+ l)-x регистров, |о т л .и ч а ю щ и и с я тем, что, 1с целью увеличения периода формируеCpus.Z
П
мых последовательностей, в него введены счетчик и преобразователь кодов, причем тактовый и установочный входы генератора подключены к тактовому и установочному входам счетчика, выход которого через преобразователь кодов подключен к (Р+1)-му входу блока сложения.
Фиг.З
Фиг.

| Гордон, Hagur | |||
| Локализация неисправностей в микропроцессорных системах при помощи шестнадцатиричных ключевых кодов | |||
| - Электроника, 1977, № 5, с.23-33 | |||
| Устройство для контроля двоичных последовательностей | 1983 |
|
SU1116431A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
1988-04-15—Публикация
1986-09-22—Подача