W
Изобретение относится к вычислительной технике и может быть использовано в системах аппаратного контроля вычислительных устройств.
Цель изобретения - расширение функциональных возможностей за счет осуществления обратного преобразования кодов.
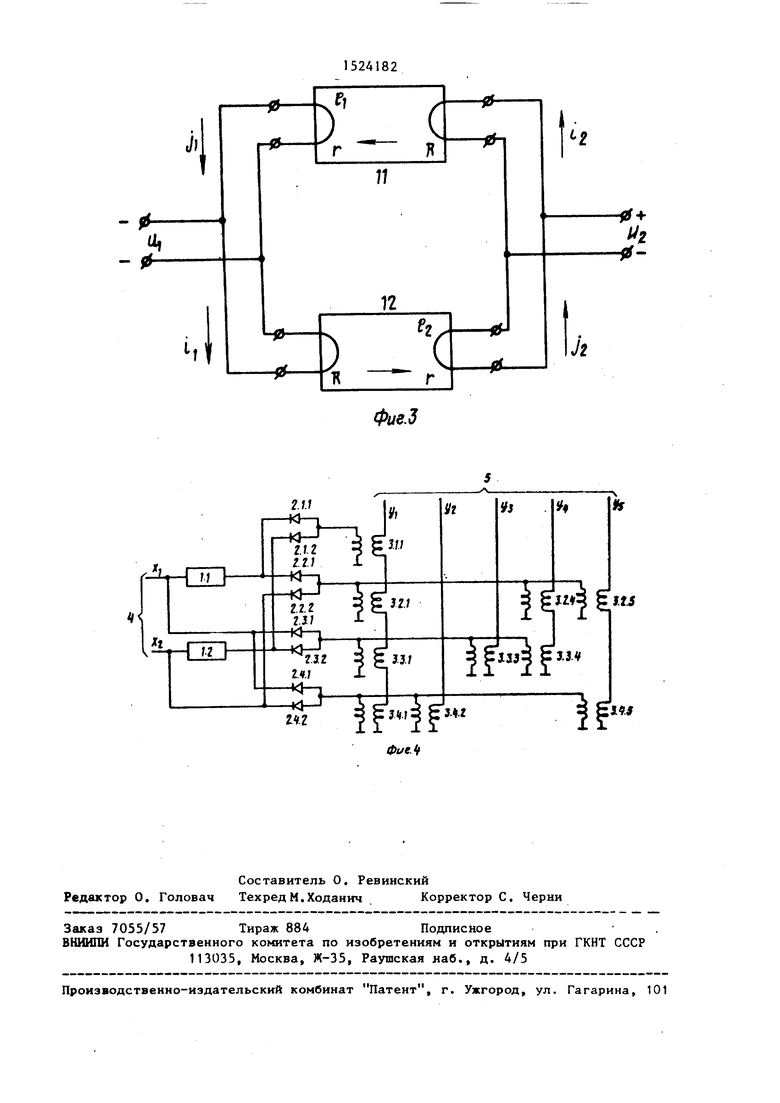
На фиг. 1 представлена функцио- напьная схема преобразователя; на фиг. 2 - элемент НЕ для непрерьшных сигналов; на фиг. 3 - трансформатор; на фиг. 4 - схема преобразователя для конкретного вида преобразования.
Преобразователь кодов содержит К элементов НЕ 1 для непрерывных сигналов (К - число входных логических пе ременных), М групп по К диодов 2 и матрицу 3 размерностью Mxj (J - числ выходных логических переменных, М - число слов входного кода). На фиг. 1 обозначены первые 4 и вторые 5 вьюо- ды.
Элемент НЕ 1 для непрерьшных сиг- налов (элемент НЕЙ) содержит (фиг. 2 первый 6 и второй 7 трансформаторы, источник 8 постоянного напряжения, а также имеет первый 9 и второй 10 выводы.,
Трансформаторы матрицы 3 и элементов 1 являются трансформаторами постоянного тока и могут быть вьтолнены (фиг..3),.например, на первом 11 и втором 12 оптеэлектронных преобразо
вателях. Кроме того, на фиг. 1-4 приняты следующие обозначения: z - потенциал на выходе т-й группы 2.т диодов (,М); у. - потенциал на выводе 5.J (,J); х - потенциал на вы воде 4.k (,K) или на вьшоде k-ro элемента НЕЙ 1 .k; х - потенциал на выводе 10 k-ro элемента ИЕН 1.k; U - напряжение источника 8 постоянного напряжения, входящего в состав элементов НЕН 1, и потенциал, соответствующий логической 1 (потенциал, соответствующий логическому О, равен нулю); х - вектор потенциалов
IJ; X - вектор потенциалов у X
вектор потенциалов
у;;
Z - вактор
потенциалов z,; xl - потенциал на первом вьшоде k-ro диода 2.m.k m-й группы.
Преобразователь функционирует следующим образом.
На вьшодах 4 и 5 присутствуют векторы X и у соответственно, Преобразователь вычисляет вектор у при данном векторе х (.прямое преобразование ) или вычисляет вектор х при данйом векторе у (обратное преобразование) . Зависимость между векторами X и у в обоих случаях описана в табл. 1 истинности
Таблица 1
1
О... 1... О 1 1
М -
Табл. 1 устанавливает связь между векторами хну.
Назовем правую и левую части табл. 1 матрицами G и В соответственно. Обозначим через элемент матрицы G, находящийся в т-й строке и J-M столбце этой матрицы. Матрица G описьшает схему соединения трансформаторов 3.m.j в матрице 3. Точне если
1, то существует трансформато 3.in,j;
s
о, то трансформатор 3.m,j.отсутствует.
5
0 5
0
5
ь.Г
Обозначим через элемент матрицы 6, находящийся в т-й строке и k-M столбце этой матрицы. Матрица В опи- сьшает схему соединения выводов элементов НЕН 1 с входами диодов 2. Точ- lee, если
1, то вывод 9 элемента НЕН I.k соединен с входом k-ro диода 2.jn.k m-й группы;
О, то вывод 10 элемента НЕН соединен с входом диода 2.p.k р-й группы, ,М, pi m; -1, то диоды группы 2.т не соединены с элементом НЕН 1.k (т.е. значение переменной х в т-й строке табл. 1 истинности не определено). Таким образом, т-й строке матрицы В соответствует группа 2.т диодов.
Табл. 1 будем назьюать правильйой, если она удовлетворяет следующим условиям:
gr,j-(0,l), (2)
т.е. матрица G является бинарной;
g
mt
1,
(3)
т.е, жит
первый столбец матрицы G содер- только
А(ь,-ь,
)-о.
(А)
т.е, каждый столбец матрицы В содержит не менее одного О и не менее одной
. )
т.е. матрица В не имеет равных строк
(0,l), (6) т.е. матрица В является бинарной (в каждой строке табл. 1 определены зна чения всех входных переменных);
Д (.)-O, (7)
т.е. в матрице О нет равных строк.
Пример правильной таблицы истинности приведен в табл. 2.
Далее рассматриваются только преобразователи, описываемые правильными таблицами (фиг. 4).
Если рассматривать двоичные коды х и у, представленные в табл. 2, как двоичные числа х и у, то легко устано-35 вить, что эта таблица описьшает функцию у 3х+16.
, Преобразователь (фиг. 4) в режиме прямого преобразования вычисляет зту
трансформатор 3.m.j ет, что
или
Г
G z-y
Из фиг. 1 следу
(12)
(13)
Потенциал на выходе группы 2.т
Zn xJu;(14)
(15)
г, k|U
Из соотношения (11) и условия (6)
функцию, а в режиме обратного преобра- следует, что элементы НЕН 1 обеспе
-
10
к;
а- 15
15241826
ричной обноток- трансформатора соответственно (фиг. 3).
Элемент НЕН 1 (фиг. 2) содержит два трансформатора 6 и 7, напряжения и токи в которых связаны соотношениями
1«1
х-х
- / х«х ,
где 1 8
(10) постоянного
1,.ч
I
20
25
об
ток источника напряжения;
токи первичных обмоток первого 6 и второго 7 трансформаторов;
X -напряжения на первичных обмотках первого 6 и второго 7 трансформаторов; X - напряжения на вторичных обмотках первого 6 и второго 7 трансформаторов.
Соотношения (10) следуют из (8) и (9). Из (10) находим
. (11) Именно в связи с этим данный элемент целесообразно называть элементом НЕ для непрерывных сигналов или сокращенно элементом НЕН.
При преобразователь содержит
трансформатор 3.m.j ет, что
Из фиг. 1 следуили
Г
(12)
G z-y
(13)
Потенциал на выходе группы 2.т
Zn xJu;(14)
(15)
г, k|U
Из соотношения (11) и условия (6)
дует, что элементы НЕН 1 обеспе



| название | год | авторы | номер документа |
|---|---|---|---|
| Табличный преобразователь кодов | 1989 |
|
SU1649669A2 |
| Дешифратор для исправления ошибок | 1985 |
|
SU1305873A1 |
| Многоканальный фотометр | 1987 |
|
SU1492224A1 |
| Скалярный умножитель векторов | 1988 |
|
SU1619254A1 |
| Устройство для решения систем линейных алгебраических уравнений | 1985 |
|
SU1347085A1 |
| Оперативное запоминающее устройство | 1989 |
|
SU1705870A1 |
| Цифроаналоговый преобразователь и способ его настройки | 1985 |
|
SU1324114A1 |
| ПРЕОБРАЗОВАТЕЛЬ КОДОВ ИЗ ОСТАТОЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ПОЛИАДИЧЕСКУЮ | 1973 |
|
SU407301A1 |
| Устройство для контроля линейного объекта управления | 1989 |
|
SU1753454A1 |
| Регулятор для оптимизации управления | 1984 |
|
SU1339492A1 |

Изобретение относится к вычислительной технике. Его использование для аппаратного контроля вычислительных устройств позволяет расширить функциональные возможности за счет осуществления обратного преобразования кодов. Преобразователь содержит матрицу 3 трансформаторов. Благодаря введению диодов 2 и элементов НЕ 1 для непрерывных сигналов один и тот же преобразователь может выполнять как прямое (от выводов 4 к выводам 5), так и обратное выводов (от 5 к 4) выводам преобразование кодов. 1 з.п. ф-лы, 4 ил.
зования вычисляет обратную ей функцию
. (у-16).
Трансформатор является узлом с двуя обмотками, напряжения которых равы, а токи противоположно направлены (в одной обмотке - от начала к концу, а в другой - от конца к началу). Эти напряжения и токи постоянны, и трансорматор может передавать энергию постоянного тока в любом нз двух направлений (из первой обмотки во вто- рую, или наоборот). Этот трансформаор описывается уравнениями
(8) (9)
- напряжение и ток первичной и втогде
е .
. I ii
е e
. . I -i«i
H II
e , 1
45
чивают выполнение равенства
х .Ь|, Х„+()(и-Хц). (16) В режиме прямого преобразования на вывод 5.1 подается потенциал у - и. Кроме того, на вьшоды 4 подается вектор X, соответствующий т-й строке табл. 1, т.е. на каждый вывод 4.k подается потенциал
50
x b«iiu. Из (16) и (17) следует
(17)
55
или
f
т.е.
,,к Ь„ьМ1-Ь к)(-Ьтк)и
, Ги при ,,; о при bpiyrtb v.
K|u °() .
Из условия (5) следует, что пр найдется такое k, при котором Ь|ц,а . При этом из (18) следует, что
0.1
:U. J
min xL..
х
Совмещая (15) i ГО т; (- и при|и т, Далее из (3) и
(19) (19), получают
(20)
(12) получают (21) .
Сравнивая (20) и (21), находят
(22)
Г U при JU т; О при |ц
Из (12) и (22) следует, что (23)
т.е. вектор у соответствует т-й строке табл. 1. Следовательно, если на вьшоды 4 подан вектор х, соответствующий некоторой строке табл..1, то на вьшодах 5 возникает вектор у, соответствующий той-же строке. Необходимым для этого условием является правильность табл. 1 и наличие потенциала у, и.
В режиме обратного преобразования на вьшоды 5 подается вектор у, соответствующий т-й строке табл. 1, т.е. на каждый выход 5.J подается потенци ал
y gmru(24)
Совмещая (12) и (24), находят:
f,, (25)
При з г из (3) ч (25) получают:
21 ,
|W
(25а)
Будем назьгоать таблицу истинности автомата правильной таблицей ранга R, если она равняется правильной, а матрица G имеет ранг R (ранг матрицы равен максимальному числу линейно-независимых строк или столбцов). Далее рассматриваются правильные таблицы ранга М, у которых ранг равен числу М строк. В таких таблицах матрицы G и G имеют ранг М,.Например, в табл.2 изображена правильная таблица ранга .
М1#
Рассмотрим векторы у - у и z
I
Z.
При выполнении условия (24) вектор у совпадает с одним из столбцов матрицы G. Поэтому ранг расширенной
матрицы С равен рангу матрицы С , т.е. равен М.Итак, в уравнении у ранги матриц равны числу М неизвестных z. Следовательно, это уравнение имеет единственное решение. Очевидно, уравнение (13) также имеет единственное решение.
Легко убедиться, что при вьтолне- нии условия (24) вектор с компонентами
5
0
5
(U при ju О при |u
(lo при рМ 26) является решением уравнения (13). Но, решение этого уравнения является единственным. Следовательно, в преобразователе, реализующем правильную таблицу истинности ранга М, при выполнении условия (24) потенциалы Z., принимают значения (26). Из (14) и (26) следует
при|и т; (27) при|и т (28) Из условия (4) следует, что существует jUrm, для которого
xL U-X|cm. (29)
Объединяя (8) и (29), получают и-х ,„-0.. (30)
0
5
0
5
0
5
Объединяя (27) и (3),
Urn
u.
получают (31)
I Из (31) и (16) получают x(.-1) u. .
Затем, учитьшая (6), находят
.u (32) Итак, из (24) следует (32). Следовательно, если на вьшоды 5 подан вектор у, соответствующий некоторой строке табл. 1, то на выводах 4 возникает вектор X, соответствующий той же строке. Необходимым для этого условием является то, чтобы табл. 1 была правильной таблицей ранга М.
Таким образом, табличный преобразователь кодов может вычислять прямую и обратную функции, определенные правильной таблицей истинности ранга М. Применение предлагаемого преобразователя в вычислительных устройствах с аппаратным контролем позволяет уменьшить объем этих устройств за счет совмещения функций прямого и обратного преобразования в одном преобразователе, уменьшить номенклатуру разнотипных узлов (по той же причине), увеличить степень охвата этих устройств аппаратным контролем, так как каждый автомат может быть проконтролирован путем вычисления обратной функции на нем же.
В свою очередь, эти причины увеличивают надежность вычислительных устройств и, как следствие, надежность систем управления, в которых они ис-- пользуются.
Формула изоб
р е т е и и я
. Преобразователь кодов, содержа щий матрицу трансформаторов (М - число слов входного кода, , К - число входных логических переменных, J - число выходных логических переменных) , первые и вторые выводы пер- вичных обмоток всех трансформаторов т-й строки (,М) матрицы соответственно объединены, вторичные обмотки всех трансформаторов j-ro столбца (J I, J) матрицы соединены последовательно и подключены к общей шине, отличающийся тем, что, с целью расширения функциональных возможностей за счет осуществления обратного преобразования кодов, в преобразователь введены М групп по К диодов и К элементов НЕ для непрерывных сигналов, первый вывод к-го элемента НЕ для непрерывных сигналов (,K) соединен с первым вьшо- дом к-го диода т-й группы при равенстве единице к-й входной логической переменной в т-м слове входного кода, второй вывод к-го элемента НЕ для не
0
Q г
5
0
прерывных сигналов подключен к первому вьшоду к-го диода р-й группы (р- Г,М,) при равенстве нулю к-й входной логической переменной в р-м слове входного кода, вторые вьюоды всех диодов т-й группы (т-1,М) объединены и подключены к первым выводам первичных обмоток трансформаторов т-й строки матрицы, вторые вьшоды которых подключены к общей шине, первые выводы элементов НЕ для непрерывных сигналов и первые выводы вторичных обмоток трансформаторов первой строки матрицы явл яются соответственно первыми и вторыми выводами преобразователя.
Фие.2
lf.2
:iw
| Авторское свидетельство СССР 1193825, кл | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Дешифратор для исправления ошибок | 1985 |
|
SU1305873A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
1989-11-23—Публикация
1988-01-04—Подача