Изобретение относится к цифровым вычислительным машинам и может быть использовано в самых различных областях народного хозяйства, где имеется потребность в специализированных вычислителях на основе тейлоровских (Т) преобразователей. ,
Цель изобретения - снижение аппаратурных затрат.
На чертеже представлена схема устройства для вычисления свертки.
Устройство содержит правую треугольную матрицу вычислительных модулей - 1 (i,j), i,,k+1, i+j k+2,2k+2 (k+1 - размерность выходного вектора), выполненных в виде управляемых сумматоров, первую - 2 (i) и вторую - 3 (i) группы регистров, первую (j) и вторую - 5 (j) группы информационных входов, первый - 6 и
второй - 7 управляющие входы, группу выходов - 8 (i).
Управляемые сумматоры и регистры второй группы выполнены п-разрядными, регистры первой группы - 2п-разрядны- ми (п - разрядность элементов входного вектора).
2п-разрядные регистры 2 предназначены для накопления промежуточных результатов вычислений и формирования в нем после п циклов окончательного результата умножения.
n-разрядные регистры 3 предназначены для хранения старших п разрядов соответствующих 2п-разрядных регистров 2, которые являются значениями первых слагаемых управляемых п-разрядных сумматоров 1 диагонали треугольной матрицы управляемых п-раз- рядных сумматоров 1.
сп
со
tsp
СО 4
Управляемые n-разрядные сумматоры 1 предназначены для сложения двух i-разрядных слагаемых.
Операции свертки соответствует выражение
Z(k) -Zx(k-l)YU) I r0
(1)
или при Z(0)X(0)Y(0)
. .. Z(1)X(1)Y(0)+X(0)Y(1)
Z(2)-X(2)Y(0)+X(1)Y(1)+X(0)Y(2)
ZaO-X(k)Y(0)+X(k-iJY(i) + . +
+X(0)Y(k)
Выражение (2) можно представить в виде произведения


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления скалярного произведения двух векторов | 1981 |
|
SU955088A1 |
| Модуль для логических преобразований булевых функций | 1989 |
|
SU1667050A1 |
| Устройство для вычисления булевых дифференциалов | 1989 |
|
SU1777132A1 |
| Устройство для вычисления логарифмов чисел | 1980 |
|
SU932491A1 |
| Устройство для вычисления скалярного произведения двух векторов | 1981 |
|
SU1179369A1 |
| Декодер кода Рида-Маллера первого порядка по максимуму правдоподобия | 1990 |
|
SU1775857A1 |
| Устройство для умножения чисел | 1990 |
|
SU1714595A1 |
| Вычислительный преобразователь информации | 1985 |
|
SU1330642A1 |
| НЕЙРОПРОЦЕССОР, УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ ФУНКЦИЙ НАСЫЩЕНИЯ, ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО И СУММАТОР | 1998 |
|
RU2131145C1 |
| Устройство для вычисления гиперболических функций у = @ и у = с @ | 1990 |
|
SU1735845A1 |
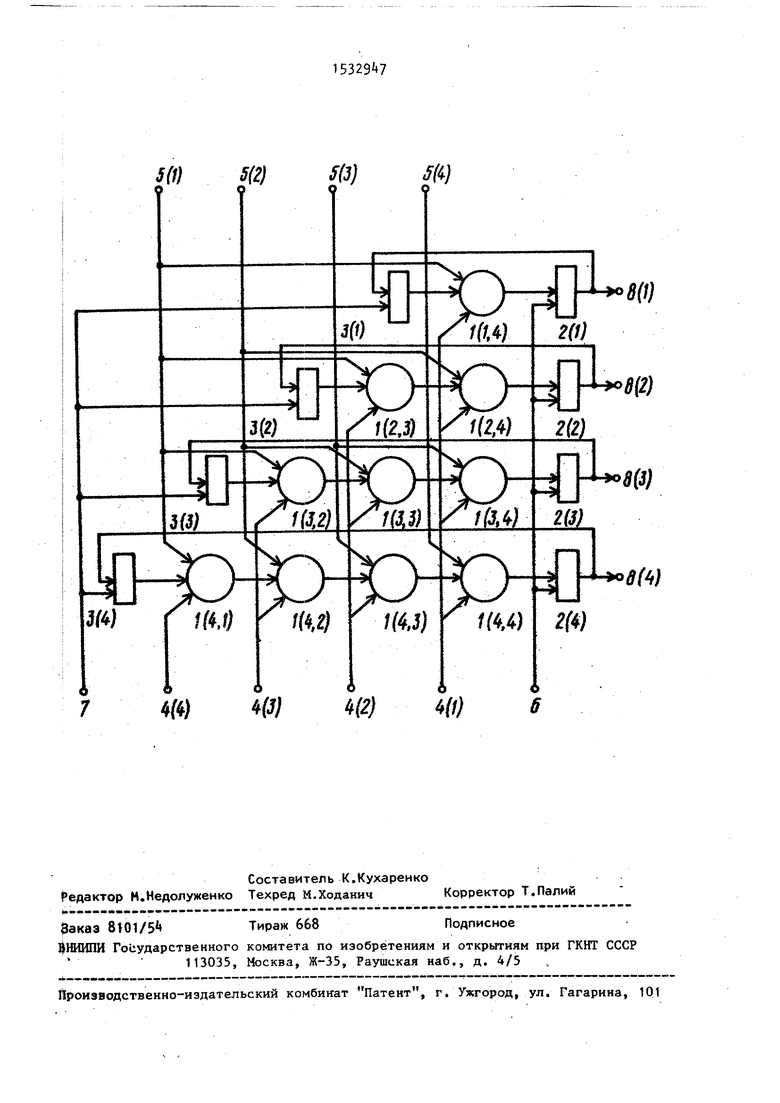
Изобретение относится к цифровой вычислительной технике и может быть использовано автономно или в составе ЭВМ в качестве вычислителя свертки. Цель изобретения - снижение аппаратурных затрат. Результат вычислений образуется через N циклов суммирования операндов, хранящихся в N-разрядных регистрах и подаваемых на информационные входы сумматоров, на управляющие входы которых подаются значения разрядов вторых сомножителей. Особенностью работы устройства является параллельно-поточная организация вычислений. 1 ил.
представляет собой сокращенную ленточную матрицу, столбцами которой являются векторьМС 1 -Х(0) Х(1) Х(2) ...,Х(Ю,где ,k, причем k-й столбец сдвинут на один элемент вниз относительно (k-l)-ro столбца.
Обозначим
Y(0)
Y(D
Z(0) Z(1)
Y(k) Z(k) Сформируем вектор бинарных элементов из m-ых компонент элементов вектора Y lj.
(0) Y4t) Y(2)Y(k), (b)
где ,1, a n-разрядность элементов вектора .
Тогда значения элементов вектора можно определить следующим образом:
i 2- -«x-Mv0+z i (5)
П t- Лiba-LJ И-(, ч
,
Рассмотрим численный пример, когд
k-0,3.
Элементы вектора представим в двоичной форме с четырьмя разрядам (п) после запятой, а элементы вектора X l} представим в десятичной форме.
Пусть Х(0)0.3 Y(0)0.1011 Х(1)0.2 Y(1)0.0101 Х(2)0.7 Y(2)0.11-01 Х(3)0.6 Y(3)0.1001 Согласно выражению (5) на первом шаге получим
для Z(0)X(0)Y(0)2H-bO,,Ol8;
для Z(1)X(1)Y(0)+X(0)Y(1) 2-40,2-1+0,3«l)«0,03;
для Z(2)X(2)Y(0)+X(1)Y(1) + +X(0)Y(2)0,075; для Z(3)X(3 Y(0)4-X(2)Y(1) +
+X(t)Y(2)+X(0)Y(3)0,11.
Определим значения
для Z(0)Z(0)4-X(0)Y(0)0,018+ +2-3-1-0,,05625;
для Z(1)Z(1) + Tx(1)Y(0)+X(0)Y(1)l 0,0925;
для Z(2)Z(2)(2)Y(0)+X(1)Y(1)+
+X(0)Y(2) 0,1625;
для Z(3)Z(3)(3)Y(0)+X{2)Y(1)+
+X(1)Y(2)+X(0)Y(3) 0,1875.
Аналогичным образом определим значения
для Z(0)Z(0)+X(0)Y(0)0,05625;
для Z(1)Z(1)+X(1)Y(0)+X(0)Y(1) 0,1675;, г г г } для Z(2)Z(2)-fX(2)Y(0)+X(1)Y(1) +
+X(0)Y(,2875;
для Z(3)Z(3)+X(3)Y((2)Y(1)+ -Х(1)|(2)+Х(0)(3)
После последнего шага получим конечные значения элементов вектора для Z(0)Z(0)+X(0)Y(,20625;
для Z(O Z(1)(1)(0)-f fX(0)Y(D 0,2675;
для Z(2)Z(2)+X(2)Y(0)+X(1)Y(1b
+X(0)Y(,7875;
для Z(3)Z(3)+X(3)Y(0)+X(2)Y(1)+
+Xd)Y(2)+X(0)Y(3) 0,9625.
Устройство работает следующим образом.
На входы первой группы информационных входов 4(1), М2), МЗ), М1) подаются значения переменных Х(0), Х(1), Х(2), Х(3) соответственно.
На входы второй группы информационных входов 5(1), 5(2), 5(3), 5 СО подаются значения младших разрядов
Y(0), Y(1), Y(2), Y(3) переменных Y(0), Y(1), Y(2), Y(3) соответственно. С подачей сигнала на второй управляющий вход 7 и в 2п-разрядных регистрах 2 образуются значения
Z(0) X(0)Y(0);
Zd)(1)Y(0)+X(0)Y(1)3 Z(2)(2)Y(0)+Xd)Yd) +
+X(0)Y(2) ; Z(3)(3)Y(0)+X(2)Y(1) +
+Xd)Y(2)+X(0)Y(3)
соответственно. После подачи сигнала на первый управляющий вход 6, старши k разряда содержимого 2п-разрядных регистров 2 записываются в соответствующие n-разрядные регистры 3.
В начале второго цикла на входы второй группы информационных входов 5(1), 5(2), 5(3), поступают значения следующих разрядов Y(0), Yd),
Y(2), Y(3) переменных Y(0), Yd), Y(2), Y(3) соответственно. С подачей сигнала на второй управляющий вход 7 в 2п-разрядных регистрах 2 образуютс
значения
Z(0)Z(0)(0)Y(0);
Zd)Zd)))+X(0)Yd)j ; г « г э з Z(2)Z(2)(2)Y(0)+Xd)Yd) +
+X(0)Y(2)} j
Z(3)Z(3)(3)Y(0)+X(2)Yd) +
+Xd)Y(2)+X(0)Y(3)
соответственно. После подачи сигнала на первый управляющий вход 6 старшие Ц разряда содержимого 2п-разрядных регистров 2 записываются в соответствующие n-разрядные регистры 3.
Через четыре цикла на выходах 8(1), 8(2), 8(3), 8Ц) образуются результаты вычислений Z(0), Z(1), Z(2), Z(3) соответственно.
Формула изобретения
Устройство для вычисления свертки, содержащее матрицу (i,j), i,,k+1, (k+1 - размерность выходного векто- pa) вычислительных модулей, причем выход (1,т)-го вычислительного модуля соединен с первым информационным входом (1, т+1)-го вычислительного модуля.
,k+1, ,k, отличающ е е с я тем, что, с целью снижения аппаратурных затрат, матрица вычислитель нь1х модулей выполнена треугольной. (, 2k+2), каждый вычислительный модуль выполнен в виде управляемого сумматора и в устройство дополнительно введены первая и вторая группы регистров, причем информационный вход i-ro регистра первой группы соединен с выходом (i,k+1)-го вычислительного модуля, а управляющие входы всех регистров первой группы соединены с первым управляющим входом устройства, выход 1-го регистра первой группы является i-м выходом группы выходов устройства, выход 1-го регистра второй группы соединен с первым информационным входом (i,i)-ro вычислительного модуля, а информационный вход 1-го регистра второй группы соединен с i-м выходом устройства, управляющие входы всех регистров второй группы соединены с вторым управляющим входом устройства, второй информационный вход (i,j)-ro вычислительного модуля соединен с j-м входом первой группы информационных входов устройства, а управляющий вход (i,j) го вычислительного модуля соединен с n-м входом второй группы информационных входов устройства (n i+j-k-1).
sm
т
w
°t{2)
°aM
| Kung H.T., Ruane L.M., Yen I.W.L | |||
| A two level pipelined systolic array for convolutions | |||
| Proc | |||
| Conf | |||
| on VLSI syst | |||
| and comput., oct | |||
| Приспособление для изготовления в грунте бетонных свай с употреблением обсадных труб | 1915 |
|
SU1981A1 |
| Springer - Verlag, 1981, p.255-26, fig-1 | |||
| Авторское свидетельство СССР № , кл | |||
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1989-12-30—Публикация
1988-05-30—Подача