Устройство для перевода числа, представленного в системе остаточных классов, в полиадическую систему счисления Советский патент 1991 года по МПК H03M7/18 

Изобретение относится к автоматике и вычислительной технике, в част- .ности, к вычислительным машинам и устройствам, функционирующим в систе- ме остаточных классов (СОК, и является усовершенствованием устройства по авт.св. № 652556.

Цель изобретения - расширение функциональных возможностей за счет преобразования числа, представленного в системе остаточных классов, в двоичный код.

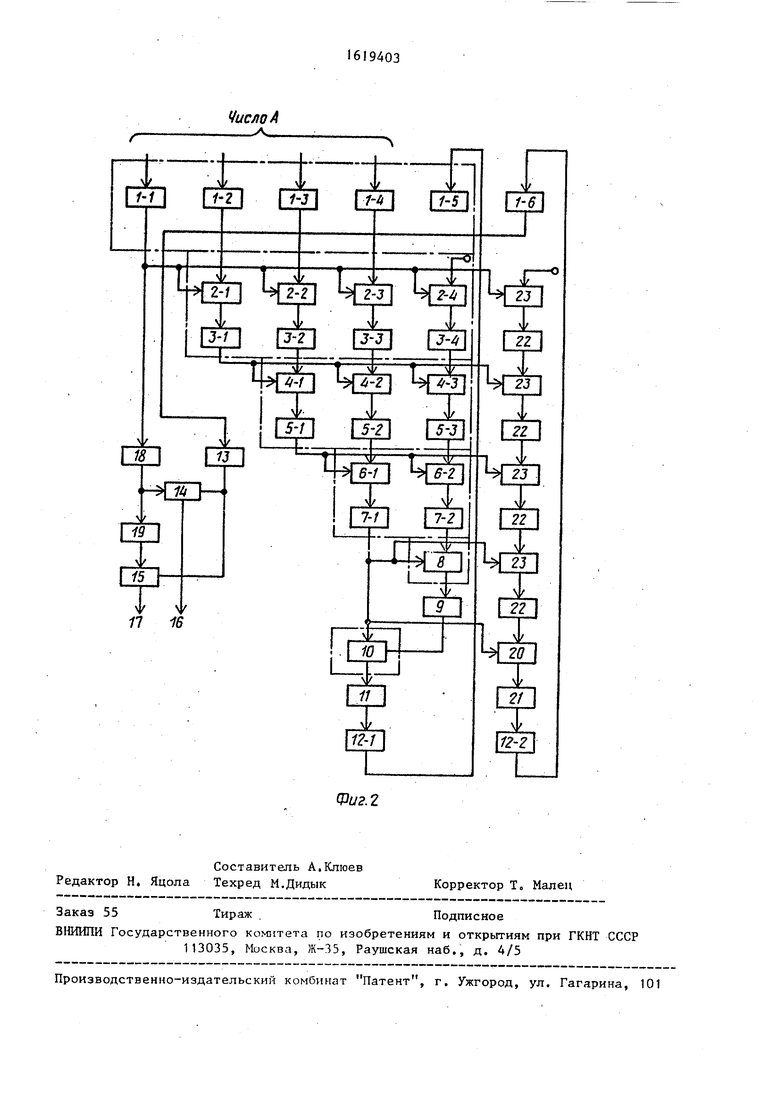
На фиг. 1 представлена схема устройства для перевода числа, представ- ленного в системе остаточных классов, в полиадическую систему счисления; на фиг.2 - пример реализации устройства для перевода числа, представленного в системе остаточных классов, в полиадическую систему счисления для .

Устройство содержит входные регистры 1-1 - l- (3n+2)t первую ступень матриц элементов И 2-1 - 2-п, первую группу элементов ИЛИ 3-1 - 3-п, вторую ступень матриц элементов И 4-1 - 4-(п-1), вторую группу элементов ИЛИ 5-1 - 5(п-1), (п-1)-ю ступень матриц элементов И 6-1 и 6-2, (п-1)-к группу элементов ИЛИ 7т1 и 7-2, n-ю ступень матриц элементов И 8, n-ю группу элементов ИЛИ 9, элемент И ,10, элемент ИЛИ 11, преобразователь 12-1 ,полиадического кода в двоичный, допол нительный преобразователь 12-2 полиадического кода в двоичный код, второй элемент ИЛИ-НЕ 13, первый дополнительный элемент И 14, второй допол

0

5

с

.,-

0

5

0

нителышй элемент И 15, выходы 16 и 17 признака минимального числа и признака максимального числа устройства соответственно, первый элемент ИЛИ-НЕ 18, элемент НЕ 19, матрицу элементов И 20, блок 21 элементов ИЛИ группу блоков 22 элементов ИЛИ и группу матриц элементов И 23.

Известное устройство позволяет осуществить расширение диапазона представления числа А в СОК, т.е. по известным остаткам числа A(tf| ,,..,), соответствующим некоторым (модулям Р,РЈ,... р,; определяет значение остатка 0( п.ц этого же числа для другого основания Pf,41 (дополнительного) . Если в качестве дополнительного основания р n-н выбрать число рп-и Р-, где т - основания (i-1, п+), Р -диапазон представления чисел в СОК, ар;- вэаимо- простые числа, то остаток по основанию Рцлц равен двоичному коду числа, для которого получаем расширение диа- пазона

Пусть остаток в СОК, основаниями которой выбраны числа Р ,Рг ,...РП задано число A(tft, #2,... ,0fn) , лежащее в интервале Ј0,РЦ. Необходимо найти вычетЛп по дополнительно введенному модулю Для этого согласно алгоритму в разряде по модулю р , остаток по которому необходимо получить, записывается 0; в разрядах по модулю Р,, и РП41 параллельно вычисляются величины ап.(и Q (А - коэффициент полиадической системы счисления).

1619403

SCЈi (modpn)-0(

Pt

(modPn)

Изобретение является усовершенствованием устройства по авт. св. № 652556, относится к автоматике и вычислительной технике и может быть использовано в вычислительных маши

Pn-,

(modpn,,)-o;(;

Q

P«fl-1

. lj-2) rt 2

где od(- -r - для ,3,.. ,riP -1До)

при0(; «;;

Wn-и U(aft4-Q) (modPru,), где tf й-н остаток числа А по основанию Г Иц.1

при § ,П р- (mod pn.. ) .

,,1l|-t

Таким образом можно получить двоич ный позиционный код числа А, заданного в СОК из интервала (О, Р-1),

ПриоЈт, 0 возможны два случая. Если остатки по каждому основанию равны нулю, то , но есль (, а.остаток, например, по первому основанию не равен нулю, то , так как oi „и (Р-1) (mod (P-1)) 0. Исходя из рассмотренного алгоритма, можно предположить, что при его технической реализации возможно проведение ряда этапов двух различных немодульных операций на однотипных узлах устройства

На фиг,1 в качестве основной системы взяты n оснований, соответствующие входным регистрам 1-i (,n), в качестве дополнительных - соответ- ствует регистрам 1-(п+1), 1-(п+2). Во входных регистрах по каждому основанию представлены остатки числа А. Код числа А принимается на входные регистры 1-i. На входном регистре 1(п+1) получаем расширение представения числа А, на входном регистре 1-(п+2) - двоичный позиционный код числа. Функционирование устройства по передаче остатка в дополнительные регистры 1-(п+1), 1-(п+2) роисходит по одному алгоритму, поэтоу при рассмотрении работы устройства остаточно разобрать действия, котоые происходят при получении остатка о модулю Рп+2. Этот случай является

(modPn);

-a

(П-2)

n-i

0dPn41 ).

,

предельным случаем расширения диапазона с некоторыми ограничениями, но 20 позволяет с небольшими нарушениями однородности структуры устройства получить результат еще одной немодульной операции. Сигналы на выходах элементов ИЛИ-НЕ 18 и 13 будут в том 25 случае,когда остатки в соответствующих регистрах 1-1 и 1-(п+2) будут равны нулю. Каждой матрицей элементов И 23 выполняется действие (o/;-0/t)iaod р-, причем с tfn«r° 30 Каждый элемент ИЛИ 3 групп и блок 22 элементов ИЛИ выполняет действие:

(,) mod Pn(p--) а( и т.д. Элемент И 10 определяет результат 35 (an-i Q)m°d Ph.,, а матрица элементов И 20 определяет результат (an.,--Q)x

mod . Блок 21 элементов ИЛИ определяет P4XP2 ... Prix()

mod Pn nt2

40 Рассмотрим работу устройства (фиг.1) для двух случаев. Первый случай - при ,Р-2, а второй при и , В первом случае устройство работает следующим образом. Код

45 числа А, для которого нужно получить двоичный позиционный код (расширение по модулю рП4. Р-1) поступает на регистры 1-i (,n). С выхода этих per гистров остатки по основаниям Р,Р„,

50 jPfl поступают на соответствующие входы элементов И матриц первой ступени 2-j(,n+l). Пройдя через усеченную матрицу элементов И, код исходного числа, преобразованный в

5 полиадическую систему счисления по

основаниям Р4,РеРи и р оступает на матрицу элементов И 20, с выхода которой через блок 21 элементов ИЛИ поступает на вход преобразователя

716194038

12-2, преобразующего полиадическийJ. Ч.7-1ПЧ -,

код числа А в остаток по основанию2 -moa V-)-J - ,

С выхода преобразователя 12-2.р

остаток передается на входной регистр г (mod 209)2 - ; 1-(п+2), Это и будет двоичный пози- .Э

ционный код числа А, Одновременно.

с этим на входном регистре l-(n-H)чг (mod 209)25 - ; получаем вычет tf nt) по другому допол-- г

нительному основанию аналогичным об- ю.р

разом.у (mod 209)2, - ;

При , oii rt 0 с выходов эле- Ч

ментов ШШ-НЕ 18 и 13 поступают сигна- В этом случае о (mod 209). лы на входы элемента И 14 и на выхо- Пример, Пусть необходимо

де 16 признака минимального числа бу- J5определить двоичный позиционный код

дет сигнал. Если , то Oi, #), ачисла , если А(1,2,4,1).

тогда сигнал будет на выходе 17 признака максимального числа..

Рассмотрим пример конкретного вы- На вход Регистра 1-1 (фиг.2) пополнения операции преобразования кодов 20ступает число на вход регистра из системы остаточных классов в двоичный} 2 число 2 на ВХ°Д регистра 1-3 - позиционный код. В качестве основнойчисло 4 и на вход Ре™стра 1-4 - чис- системы возьмем основания , ,ло 1 , разряды регистров 1-6будутв , , а в качестве дополнитель-нулевом состоянии. Дальнейшая запись по ных и Рб 2-3 5 7 209. В этом 25определению вычитов числа А по осно- случае - диапазон представленияваниям и является в не- в данной СОК0 Выбор (Р-1) некоторой степени формальной по отноше- случаен, ибо он объясняется требова-нию к фиг.2, но в достаточной степени нием того, чтобы Р6 и р (i-1,5) взаим-отражает функционирование устройства но просты, а также тем, что в данном 30при прохождении кода исходного числа случае легко определяются и соответ-А через усеченную матрицу элементов И, ственно технически реализуются следую-не требуя более детальных схем уст- щие мультипликативные величины:ройства.

Остаток числа А по основанию ) а - П Р; (mod РП+ ), тогда tfm| Ј(an,, -6)mod Р„, , где8 (rood ll)210(mod ll) l(mod И);

if (mod 209)2JO(mod 209) 1 (mod ye.(0-4) mod

5

Ck-1- (0-18 ) mod .

6

1-6

Таким образом в шестом регистре получают двоичный позиционный код числа .

При А(0,0,0,0)0 на выходе 16 признака минимального числа будет сигнал, а при А(1,2,Д,6)210-1 209 будет сигнал на выходе 17. Использование устройства позволяет унифицировать немодульные операции СОК - расширение диапазона представления чисел и преобразование в двоичный код.

формула изобретения

Устройство для перевода числа, представленного в системе остаточных классов, в полиадическую систему счисления по авт. св. № 652556, о т- личающееся тем, что, с целью расширения функциональных возможностей за счет преобразования числа, представленного в системе остаточных классов, в двоичный код, оно содержит (п+2)-й регистр, матрицу элементов И, блок элементов ИЛИ, первый и второй дополнительные элементы II, до- . полнительный преобразователь полиадического кода в двоичный код, первый и второй элементы ИЛИ-НЕ и элемент НЕ, группу матриц элементов И и группу блоков элементов ИЛИ, причем выходы разрядов первого входного регистра соединены с соответствующими входами

6

10

15

20

первого элемента ИЛИ-НЕ, выход которого соединен с первым входом первого дополнительного элемента И и через элемент НЕ - с первым входом второго дополнительного элемента И, выход которого является выходом признака максимального числа устройства, выходы разрядов (п+2)-го входного регистра соединены с соответствующими входами второго элемента ИЛИ-НЕ, выход которого соединен с вторым входом второго .дополнительного элемента И и с вторым уходом первого дополнительного элемента И, выход которого является выходом признака минимального числа устройства, выходы группы матрицы элементов И соединены с соответствующими входами блока элементов ИЛИ, выход которого соединен с входом дополнительного преобразователя полиадического кода в двоичный код, выход которого соединен с входом (п+2)-го входного регистра, выходы разрядов первого входного регистра и выходы первых элементов ИЛИ групп соединены соответственно с первыми группами входов матриц элементов И группы, выходы группы которых соединены с соответствующими входами 30 блоков элементов ИЛИ группы, соответственно, выходы разрядов выхода k-ro блока элементов ИЛИ (,..n-l) соединены с второй группой входов (k-H)-u матрицы элементов И группы, выход первого элемента ИЛИ (п-1)-й группы и выхода разрядов выхода последнего блока элементов ИЛИ группы соединены соответственно с первой и второй труп- - памн входов матрицы элементов И.

25

35

Число А v

Wi-л ч

I 4

I w Т . .Т . Y .

№3 Ч22 Ч2Ш

16

гт

11 Mil

V

ч

I 45-1

V

i

ЕЗ SI

v

аду

X

LU

сю