(54) ПРЕОБРАЗОВАТЕЛЬ ПОЛИАДИЧЕСКОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ


| название | год | авторы | номер документа |
|---|---|---|---|
| Преобразователь кодов из системыОСТАТОчНыХ КлАССОВ B дВОичНыйпОзициОННый КОд | 1979 |
|
SU813408A1 |
| Устройство для перевода чисел из системы остаточных классов в полиадическую | 1977 |
|
SU605209A1 |
| ПРЕОБРАЗОВАТЕЛЬ КОДА ИЗ СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ В ПОЛИАДИЧЕСКИЙ КОД | 1972 |
|
SU328448A1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| НЕЙРОННАЯ СЕТЬ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2008 |
|
RU2400813C2 |
| Устройство для перевода числа, представленного в системе остаточных классов, в полиадическую систему счисления | 1989 |
|
SU1619403A2 |
| УСТРОЙСТВО КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ ИНФОРМАЦИИ | 2011 |
|
RU2475838C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЕЛ ИЗ КОДА СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ В ПОЛИАДИЧЕСКИЙ КОД | 2001 |
|
RU2187886C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ПОЛИАДИЧЕСКОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2258257C2 |
| Логарифмирующее устройство | 1976 |
|
SU634272A1 |

1
Изобретение относится к вычислительной технике и может быть использовано в вычислительных устройствах для ускоренного перевода чисел, закодированных в полиадической системе счисления, в систему остаточных классов (СОК).
Известен преобразователь двоичного кода в код с любым другим основанием, использующий принцип преобразования кодов на сумматорах и логических элементах, содержащий пирамидальные сумматоры всех разрядов числа с новым основанием 1.
Недостатками известного преобразователя являются сложность устройства, невысокое быстродействие и значительный объем оборудования.
Наиболее близким по технической сущности к предлагаемому является преобразователь двоичного кода в код системы остаточных классов, содержащий входной регистр, матричные сумматоры, матрицу преобразования двоичного кода в промежуточный непозиционный код 2.
Однако известный преобразователь имеет низкое быстродействие и обладает значительным объемом оборудования.
Цель изобретения - повышение быстродействия устройства.
Указанная цель достигается тем, что в известный преобразователь, содержащий входной регистр и матричные сумматоры, 5 дополнительно введены дешифраторы и ключи, причем выходы первой, второй и третьей групп разрядов входного регистра подключены соответственно ко входам первого, второго и третьего дещифраторов, выходы
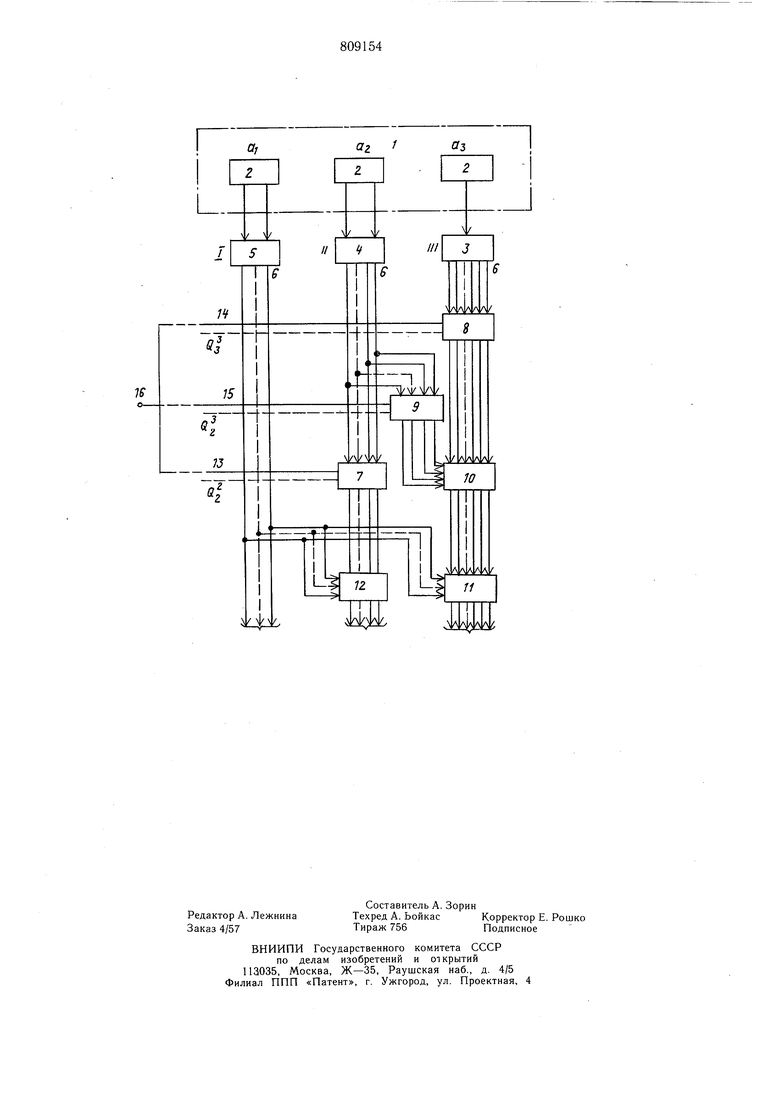
первого дешифратора подключены к входам первых групп первого и второго матричных сумматоров, выходы второго дешифратора через первый и второй ключи подключены соответственно- ко входам второй группы.первого матричного сумматора и входам первой группы второго матричного сумматора, выходы третьего дешифратора через третий ключ подключены ко входам второй группы третьего матричного сумматора, выходы которого соединены со входами второй группы второго матричного сумматора, выходы первого и второго матричных сумматоров и. первого дешифратора соединены с выходом устройства, управляющие входы ключей соединены со входом устройства. В полиадическом коде п-разрядное число А может быть представлено в виде: ,.-...anQK, (i) Qt+1 (,НХ1 1,г,...п) Тогда ,taiPlta5P,Pit.,.,H,...PnM. (г) где числа Pi, Рг,..- fn, - основания полиадического, кода. Пусть числа PI, Рг,...Рп, служат одновременно основанием системы остаточных классов (СОК) и полиадического кода. Пред ставление числа А в полиадическом коде можно записать в виде A (ai,Qi,-.-an). Диапазоны чисел однозначно представлены в построенных указанным образом СОК и полиадическом коде совпадают. Поэтому можно говорить о наличии однозначного соответствия между множеством представлений чисел в СОК A W,)o(i,...ti;,rAeo{: pesl ACmodPt), (Ul,2,...ti.)(А) и множеством представлений чисел в полиадическом коде . /(ai,aj.,...an) (5) Пусть известно представление числа А в полиадическом коде (5). Требуется найти его представление в СОК. Так как основания в СОК постоянны, то представление чисел Qi,Qz.-- Qn в СОК известны q,(M.--i), (q.o,,.Q), Cl3--(0,O.QLQj), Q..(0,0,...0,). Тогда из формулы (1) следует, что цифры , ota оСа можно найти следующим образом: в(, а, (mod PI), (woolP2)j 5 a,4aiql -aiQ|(tr,od Pj), o( c(,Qi(+...taaQn x РП). Если взять схему преобразователя полиадического кода в код системы остаточных классов для трех модулей (, Рг 3, РЗ 5), то, исходя из выражений (6), для выбранной системы модулей числа Qi, Q2 и РЗ можно представить в виде: Q 1 (1,1,1), Qa 2 (0,2,2), (0,01), а числа ai, dz. и d согласно выражению (7) можно представить в виде: d ttimodPi, c/i ai + az2modPz, ai + 2 a2-I-QjmodPa. Ha чертеже представлена схема преобразователя полиадического кода в код СОК. Преобразователь содержит входной регистр 1 с блоками 2 разрядов, дешифраторы 3, 4 и 5, которые предназначены для преобразования значения разрядов числа, представленного в полиадическом коде в код позиция-число, выходы б, представляющие остатки чисел по основаниям выбранной системы, ключи 7, 8 и 9, предназначенные для формирования произведений коэффициентов полиадического кода (cxi) и чисел Q (где 1 2, 3,...п); матричные сумматоры 10, 11 и 12, предназначенные для суммирова ни.я по соответствующему модулю значений произведений, полученных на выходе ключей, вход 13, соответствующий значению числа Qa, вход 14, соответствующий значению числа Рг, 15, соответствующий значению чисел Qz, Qj и Qj. Блоки 2 разрядов необходимы для хранения чисел, представленных в полиадическом коде. Преобразователь работает следующим образом. Код числа А, для которого необходимо получить представление в СОК, принимается на блоки 2 входного регистра 1, причем коэффициенты ai представлены в двоичной форме. Сигналы с выхода регистра поступают на вход дешифраторов 3, 4 и 5. На выходе дешифраторов образуется код позиция-число. Выходной сигнал дешифратора 5 есть остаток ai числа А по основанию Р| и поступает на выход и на вход матричных сумматоров 11 и 12. Выходной сигнал дешифратора 4 поступает на информационный вход ключей 7 и 9. Выходной сигнал дешифратора 3 поступает на информационный вход ключа 8. На управляющие входы ключей 7, 8 и 9 поступают соответственно коды чисел Qa, Qj, Qz (входы 13, 14 и 15). На выходах ключей формируются следующие сигналы: ключ 7 - сигнал, соответствующий значению Ч-гРг (mod Р) ключ 8 - сигнал, соответствующий значению QsQl (modPs) ключ 9 - сигнал, соответствующий значению ctzQz (modP;). Сигналы с выходов поступают на один из входов матричных сумматоров. Так, с выхода ключа 7 сигнал поступает на один из входов матричного сумматора 12. На вторые входы сумматора 12 поступает сигнал с выхода дешифратора 5. В сумматоре происходит сложение величинами QiQz по модулю Рг. Выходное значение сумматора 12 есть представление остатка числа А по модулю Сигналы с выхода ключей 8 и 9 поступают на вход сумматора 10, в котором формируется сумма слагаемых ctjQs + -f ajQa (mod РЗ). Выходной сигнал сумматора 10 поступает на входы сумматора 11, а на другие входы этого сумматора поступает сигнал с выхода дещифратора 5. Выходной сигнал сумматора 11 есть представление числа А по модулю Pj. Таким образом, на выходе преобразователя формируются сигналы, соответствующие представлению числа А в СОК. Если устройство реализовано на комбинационных элементах, то преобразование числа осуществляется за один такт при любом количестве модулей, при этом входы 13, 14 и 15 замкнуты (на чертеже показано пунктиром) и управляющий сигнал, соответствующий числам Qa, Qz, Qs поступает на вход 16. Если преобразователь реализован на интегральных схемах, то ему присуще простота и больщая надежность. Время преобразования определяется суммарной задержкой сигнала в блоках 3, 8, 10 и 11. Пример. Пусть известно представление числа А в полиадическом-коде А( 1,0,2). Найти представление числа в СОК. На вход регистра поданы коэффициенты Qi в двоичной форме А (01, 00, 010). На выходе преобразователь получает сигналы, соответствующие числу А в СОК, А (1, 1, 3). причем число А представлено в однопозиционном коде. Если требуется представить значения остатков в двоичной форме, то необходимо на выходе преобразователя включить щифраторы, которые представляют собой набор элементов ИЛИ, (преобразование числа для приведенного примера на чертеже показано пунктирными линиями). Использование предлагаемого изобретения в вычислительных мащинах позволяет повысить быстродействие за счет уменьшения времени выполнения операций сложения, вычитания и умножения, сокращает объем оборудования. Реализация преобразователя на интегральных схемах обеспечивает экономический эффект. Формула изобретения Преобразователь полиадического кода в код системы остаточных классов, содержащий входной регистр и матричные сумматоры, отличающийся тем, что, с целью повышения скорости вычислений, в него дополнительно введены дещифраторы и ключи, причем выходы первой, второй и третьей групп разрядов входного регистра подключены соответственно ко входам первого, второго и третьего дешифраторов, выходы первого дещифратора подключены к входам первых групп первого и второго матричных сумматоров, выходы второго дешифратора через первый и второй ключи подключены соответственно ко входам второй группы первого матричного сумматора и входам первой группы второго матричного сумматора, выходы третьего дешифратора через третий ключ подключены ко входам второй группы третьего матричного сумматора, выходы которого соединены со входами второй группы второго матричного сумматора, выходы первого и второго матричных сумматоров и первого дешифратора соединены с выходом устройства, управляющие входы ключей соединены со входом устроиства. Источники информации,. принятые во внимание при экспертизе 1.Авторское свидетельство СССР № 315176, кл. G 06 F 5/02, 1969. 2.Авторское свидетельство СССР № 525947, кл. G 06 F 5/02, 1974 (прототип).
Oj
аг /
сгз
Авторы
Даты
1981-02-28—Публикация
1979-04-13—Подача