со
с


| название | год | авторы | номер документа |
|---|---|---|---|
| Образец для испытания материалов на термомеханическую усталость | 1988 |
|
SU1539590A1 |
| Образец для испытания материалов на термическую усталость | 1986 |
|
SU1381372A1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ РОТОРА ЛОПАТОЧНОЙ МАШИНЫ | 1991 |
|
RU2047464C1 |
| ЖЕЛЕЗНОДОРОЖНОЕ КОЛЕСО (ВАРИАНТЫ) | 1994 |
|
RU2116204C1 |
| ПРОДЛЕНИЕ СРОКА СЛУЖБЫ ДИСКА СИЛОВОЙ ТУРБИНЫ, ПОДВЕРЖЕННОГО КОРРОЗИОННОМУ ПОВРЕЖДЕНИЮ ПРИ ЭКСПЛУАТАЦИИ (ВАРИАНТЫ) | 2018 |
|
RU2737127C1 |
| Токоподвод электровакуумного прибора | 1979 |
|
SU836705A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕРМОПРОЧНОСТИ ПОЛЫХ ОБОЛОЧЕК | 2005 |
|
RU2287808C1 |
| Способ установки токопроводов электрической печи сопротивления для графитации углеродных изделий | 1990 |
|
SU1753221A1 |
| УСТРОЙСТВО ДЛЯ ИССЛЕДОВАНИЯ МАЛОЦИКЛОВОЙ ТЕРМОУСТАЛОСТИ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ В ГАЗОВЫХ ПОТОКАХ | 2013 |
|
RU2546845C1 |
| Коническое зубчатое колесо для испытаний на контактную усталость | 1989 |
|
SU1795330A1 |

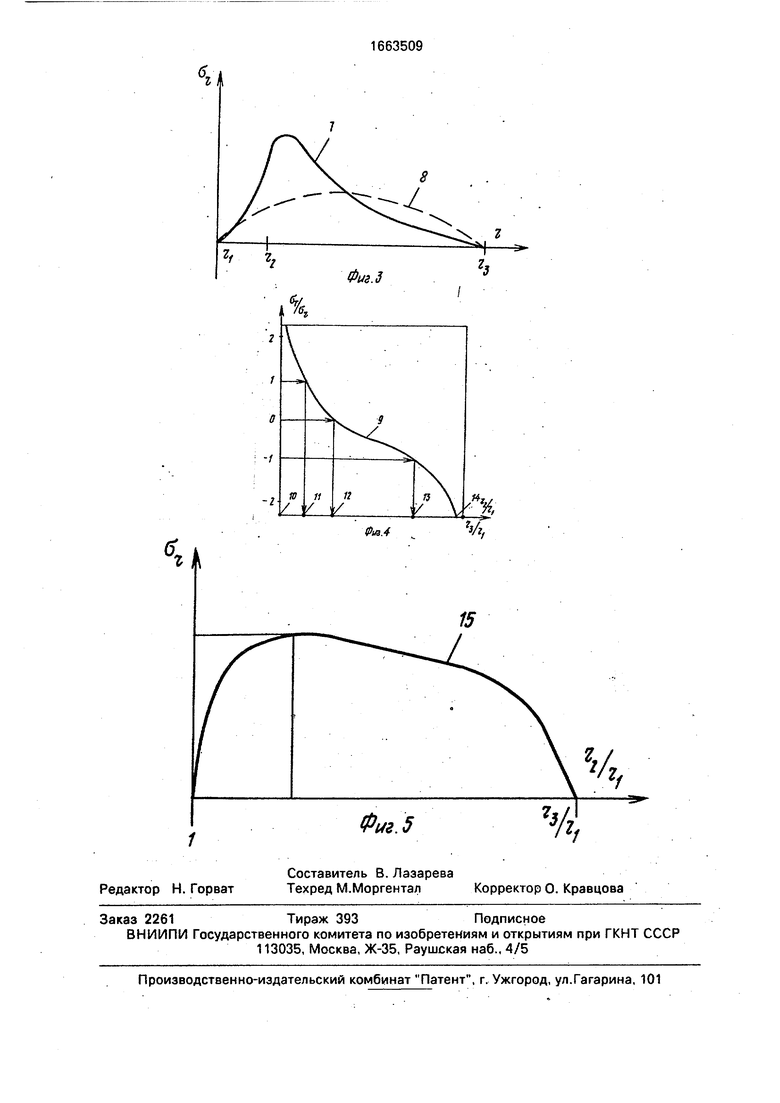
Изобретение относится к технике испытаний на прочность. Цель изобретения - расширение технологических возможностей путем определения расположения максимума радиальных термических напряжений при одних и тех же перепадах температур. Образец выполнен в виде кольца с наружной и внутренней цилиндрическими поверхностями. Часть торцевых поверхностей выполнена в виде параболлоидов, сужающихся к оси, а часть в виде гиперболлоидов, расширяющихся к оси. Образец размещают в камере и обдувают газовым потоком с заданной температурой. В образце возникают термические напряжения, величина которых зависит от геометрических размеров и термодинамических параметров. Усталость материала определяют по количеству теплосмен до появления трещин. Выполнение торцев в виде сопрягающихся поверхностей вращения дает возможность определять наиболее опасное сочетание величины главных напряжений и температуры. 5 ил.
Изобретение относится к испытательной технике, в частности к испытаниям на прочность.
Цель изобретения - расширение технологических возможностей путем определения расположения максимума радиальных термических напряжений при одних и тех же перепадах температур,
На фиг. 1 представлен пример выполнения образца, поперечное сечение, (п - внутренний радиус кольца, га - расстояние от центра кольца до минимальной толщины образца, гз - наружный радиус кольца, 1,1 - параболлическая часть торцовой поверхности, 2,2 - гиперболическая часть торцовой поверхности, 3 - боковая поверхность, 4 - внутренняя поверхность); на фиг. 2 - распределение тангенциальных 0У термических напряжений вдоль радиуса при тепловом воздействии на внутреннюю поверхность кольца в момент охлаждения (кривая 5 - для
заявляемого образца, кривая б - для образца-прототипа); на фиг. 3 - распределение радиальных о термических напряжений вдоль-радиуса кольца (кривая 7 - для заявляемого образца, кривая 8 - для образца- прототипа); на фиг. 4 - распределение
- °г соотношений главных напряжении - в образцах для определенного ЬМИн в зависимости от расположения его вдоль радиуса кольца (кривая 9); на фиг. 5 - огибающая максимумов радиальных напряжений для множества образцов с одинаковой минимальной толщиной образца Ьмин в зависимости от расположения минимума толщины образца вдоль радиуса (кривая 10).
Испытания проводят следующим образом.
Обрззец размещают в испытательной камере (не показана) и обдувают, например, через центральное отверстие газовым потоON О 00
сл о ю
ком, температуру которого изменяют по заданной программе. В результате воздействия газового потока на образец в нем возникают термические напряжения, величина которых зависит от геометрических параметров образца и термодинамических параметров газового потока. Под воздействием циклических термических напряжений в испытуемом образце возникают трещины. Термическую усталость образца определяют по количеству теплосмен до появления трещин на рабочем участке, т.е. в месте, где достигается наиболее опасное для исследуемого материала сочетание величин главных напряжений и температуры. Необходимый режим изменения теплового и напряженного состояния материала задают путем выбора параметров образца Ьмии, п, га, гз, k и п, а также программой-теплового воздействия.
Как видно из фиг. 2 (кривая 5), тангенциальные термические напряжения в кольце при неравномерном прогреве достигают максимумов по абсолютной величине, но противоположных знаков на боковой 3 и внутренней 4 поверхностях, достигая нулевого значения внутри тела образца. При соответственно одинаковых перепадах температур между внутренней и наружной поверхностями внутренних и наружных радиусов максимумы тангенциальных термических напряжений будут близкими по величине, несмотря на различие в толщине образцов и в характере изменения толщины по радиусу.
Радиальные напряжения имеют другой характер распределения по радиусу кольца: на внутренней 4 и боковой 3 поверхности они равны нулю, а внутри тела образца достигают максимального значения. Максимум радиальных термических напряжений в кольце постоянной или монотонно изменяющейся толщины существенно ниже максимума тангенциальных термических напряжений. Увеличение радиальных напряжений за счет увеличения перепада температур неизбежно приводит к увеличению и тангенциальных. Толщина образца, если она изменяется пропорционально, не влияет на величину как тангенциальных, так и радиальных термических напряжений. Например, изменение коэффициента пропорциональности К между толщиной b и радиусом г не изменит величины термических напряжений в образце-прототипе. Если толщина образца изменяется вдоль радиуса немонотонно, как показано на фиг. 1, величина максимума радиальных термических напряжений (кривая 7 на фиг. 3) может быть значительно выше. Максимум
радиальных напряжений в образце может быть больше максимума тангенциальных, Кроме того, расположение максимума радиальных термических напряжений относи;
тельно центра образца существенно зависит от расположения минимума толщины.
Таким образом, несмотря на то, что термические напряжения вызываются нерав0 номерностью распределения температур по телу кольца и их величина в основном связана с величиной перепада температур, в образце предлагаемой формы имеется возможность управлять величиной и рас5 положением максимума радиальных термических напряжений при одних и тех же перепадах температур, а следовательно, примерно при тех же величинах тангенциальных напряжений
0
Как видно из фиг. 4, кривая 9 при испытании кольцевого образца на термическую усталость материал подвергается воздействию термических напряжений при соотно5 шениях главных напряжений - от -°° до
Or
+ оо. Однако разрушение в образце-прототипе происходит, как правило, при одноосном напряженном состоянии в месте
0 действия максимальных тангенциальных напряжений, т.е. на внутренней или боковой поверхности, где радиальные термические напряжения равны нулю. Это объясняется тем, что максимум тангенциальных термиче5 ских напряжений при монотонном изменении толщины образца вдоль радиуса значительно превышает максимум радиальных термических напряжений. Таким образом для большинства материалов наиболее
0 опасным является максимум тангенциальных напряжений.
Образец позволяет моделировать разрушение от термической усталости при любом заданном соотношении главных
5 напряжений ov/crr практически всех известных материалов. Изменяя величину и рас- пояожение максимума радиальных термических напряжений при одном и том же перепаде температур и величине макси0 мума тангенциальных термических напряжений, можно получить разрушение на любом заданном (для конкретного материала) расстоянии от центра образца, т.е. при любом заданном соотношении главных на5 пряжений.
В точке 10 (кривая 9, фиг. 4) произойдет разрушение при одноосном тангенциальном растяжении (Or/Oi-:- - °°); в точке 11 - при всестороннем двуосном растяжении ( OT/OT ra 1); в точке 12 - при одноосном
радиальном растяжении (От/Or 0); в точке 13 - при чистом сдвиге (ОУ/ОГ -1); в точке 14- при одноосном тангенциальном сжатии (От/(7г - оо).
Величина и расположение максимума радиальных термических напряжений зависит от величины и расположения минимума толщины образца, но место расположения максимума радиальных напряжений не совпадает с местом расположения ми- нимума толщины, а место разрушения образца не совпадает с точкой максимума радиальных напряжений, тем более с точкой минимума толщины образца. Образец разрушится в том месте, где сочетание ве- личин главных напряжений и температуры окажется наиболее опасным для данного типа материала.
Необходимый для заданного режима нагружения закон распределения толщины образца вдоль радиуса, т.е. величина и расположение минимума или наоборот максимума толщины в свою очередь задается соответствующим выбором параметров К и п параболлоидов и гиперболлоидов торцо- вых поверхностей.
Форма образца обеспечивает возможность использования простых дифферени- цальных уравнений при расчете теплового состояния материала
1 d frn + кПЧсГГ
ji + 7Ж
для параболлоида b krn где г - текущий радиус;
Т - температура материала;
t- время;
у - коэффициент температуропроводгп+1
°t - для параболлоида (3)
г (п г
ov г -для гиперболлоида (4)
ности материала;
- it -ft-rS и
для гиперболлоида brn k,
а также при расчете напряженного состоя-
ния
d (о г +1) rndr
J-n
Интегрирование этих уравнений с учетом дополнительных условий (уравнений совместности деформаций, а также урав- нений, связывающих деформации и напряжения) дает расчетные формулы для определения термонапряженного состояния образца, т.е. образец относится к простейшим телам вращения, которые можно
5 Ю 15
20 25
30
35
40
45
50
55
рассчитывать с помощью аналитических выражений с высокой степенью точности.
Поскольку параметры К не входят в дифференциальные уравнения, выбор их величины не влияет на возможность аналитического расчета термонапряженного состояния, т.е они могут быть выбраны различными не только для параболлоида и гиперболлоида, но и для различных (1 и 1, 2 и 2) торцовых поверхностей, т.е. профиль кольца может быть несимметричным, как показано на фиг. 1.
Параметры п входят в уравнения и они должны быть одинаковы, по крайней мере в одних и тех же пределах интегрирования, т.е. для обоих (1 и 1, а также 2 и 2) торцовых поверхностей. В разных пределах интегрирования параметры п могут отличаться, т.е. параметры параболлоида могут отличаться от параметров гиперболлоида.
Выбор геометрических параметров п, Г2, гз и Ьмин, а также параметров Ki, Ki1, K2, К2 , ni и П2 осуществляют исходя из заданного режима испытаний и параметров газового потока, а также достаточно плавного сопряжения параболической и гиперболической частей торцовых поверхностей. Параметрами режима испытаний могут быть значения температур, главных термических напряжений 7г и ог и градиента этих параметров по сечению образца и во времени.
Выбор геометрических параметров осуществляют с помощью номограмм, отражающих их взаимосвязь с термонапряженным состоянием и между собой. Для уменьшения числа номограмм могут использовать- .ся безразмерные параметры теории подобия физических процессов 7г/аг, г2/п, Ьмин/П и др. Номограммы строят путем расчета теплового и напряженного состояния серии образцов при нескольких фиксированных значениях геометрических параметров. Например, на фиг. 4 кривая 9 отражает зависимость Oj/ffr от га/п при фиксированных Ьмин и всех коэффициентов К, по которой можно определить на каком расстоянии от центра образца необходимо обеспечить разрушение, чтобы оно произошло при заданном соотношении главных напряжений. По графику, приведенному на (фиг. 5, кривая 15) можно определить значения радиальных напряжений для выбранного 7г/Ог И Ьмин.
Таким образом, выбирая закон изменения толщины кольца вдоль радиуса, в заявляемом образце возможно обеспечить разрушение при любом соотношении главных напряжений. При выполнении торцовых поверхностей в виде сужающихся к центру параболлоидов и расширяющихся к центру гиперболлоидов в образце достаточно точно определяется тепловое и напряженное состояние материала благодаря возможности применения аналитических методов расчета.
Формула изобретения Образец для испытания материалов на термическую усталость, выполненный в виде кольца с внутренней и наружной цилиндрическими поверхностями, часть каждой из торцовых поверхностей которого имеет форму параболлоида и описывается урав«т
Фиа.2
нением вида b k-rn, где b - текущая координата, г - расстояние от оси; k, n - постоянные коэффициенты, отличающийся тем, что, с целью расширения технологических возможностей путем определения расположения максимума радиальных термических напряжений при одних и тех же перепадах температур, другая часть каждой из торцовых поверхностей имеет форму гиперболлоида, описываемого уравнением вида Ьт К, где К - текущая координата, и сопрягающегося на каждом торце с соответствующей поверхностью параболлоида.
8
:s 2
| Кипятильник для воды | 1921 |
|
SU5A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
Авторы
Даты
1991-07-15—Публикация
1989-06-05—Подача