На фиг. 1-2 приняты следующие обозначения: r(t) - текущий радиус кристалла, г0 - заданный диаметр цилиндрического кристалла, R - радиус тигля, гз - радиус затравки, V0 - скорость вытягивания кристалла, M(t), m(t), /и (t) - массы расплава в тигле плотностью р, кристалла плотностью р$ и мениска плотностью р соответственно в момент измерения, Mf - постоянная масса флюса плотностью pr, Hf(t) - переменная толщина флюса, отсчитываемая от фронта кристаллизации до верхней границы флюса, h{t) - текущая высота мениска, h0 - стационарная высота мениска, соответствующая цилиндрическому кристаллу диаметром 2г0, H(t) - высота расплава в тигле от дна тигля до основания мениска, /(t), а (т.) - углы наклона боковой поверхности и мениска относительно вертикали, Ј - постоянный угол роста, T3(t)- переменное время запаздывания, характеризующее время образования сечения кристалла, выходящего из-под слоя флюса в момент измерения, f(t) - текущая длина вытягиваемого кристалла
Способ реализован на автоматизированной ростовой установке, оснащенной датчиком веса, задатчиками и регуляторами мощности нагрева и скорости вытягивания, ЭВМ совместно с интерфейсным модулем. Регулирование диаметра кристалла согласно способу проводят посредством управления температурой нагрева и скоростью вытягивания монокристалла по отклонению скорости изменения измеряемого веса монокристалла и связанного с ним мениска от известной заданной величины в ходе разра- щивания. По окончании формирования начального конуса стабилизацию диаметра выращиваемого монокристалла осуществляют регулятором состояния, использующим восстановление с помощью наблюдателя величины переменных состояния - отклонения радиуса кристалла и высоты мениска от известных стационарных значений,
В тигель ростовой установки помещают исходную шихту, например арсенида галлия и порошок оксида бора. После расплавления и образования слоя защитной жидкости из оксида бора вручную осуществляют затравливание и включают автоматический режим регулирования диаметра выращиваемого монокристалла
В любой момент времени датчиком фиксируется вес
Р (t) (t) + / (t) - Fa(t) + const, (1) где g - гравитационная постоянная;
константа характеризует постоянный вес оснастки кристаллодержателя.
10
15
20
25
30
35
40
45
50
Выталкивающая сила Архимеда определяется выражением
Fa(t)-gi/(mfft)+/«(t)),(2)
где щ const;
mt(t) - масса кристалла, находящегося под слоем флюса к моменту времени t.
Если m(t) mt(t), другими словами, кристалл не вышел из-под флюса, то из (1) и (2) следует
P(t)g(1-J7)M(t),(3)
где М (t) mf (t) + /и (t) в соответствии С законом сохранения масс. Если m(t) больше m${t), т.е. кристалл выходит из-под флюса, из (1) следует
P(t) (t) + /г (t) -1, (mf (t) + p (t))
- -g (1 - J) M (t) + g 17 m {t - r3) (4) где M(t) m (t) + /i (t);
mf (t) m (t) - m (t - Гз).
Уравнения (З), (4) характеризуют структуру реального сигнала P(t) весового датчика, используемого для сравнения с программным заданием, дифференцируемого, а также запоминаемого на время Тз.
При весовом методе контроля текущего состояния динамической системы как наблюдаемой величиной, так и программным значением служит производная веса. Таким образом, программное задание должно рассчитываться как
Kt) -gd-)M(t),(5)
P(t) -g (1 - rj) M (t) + g t) - r3(t) (6)
Здесь и далее знаком л обозначаются программные значения.
Формула (5) верна до выхода конуса из- под флюса, а (6) - в более общем случае до окончательного выхода конуса из-под флюса
Вытягивание с постоянной скоростью кристалла любой формы, отличной от прямого кругового цилиндра, приводит к нелинейному во времени изменению его радиуса r(t) и веса. При расчета программного задания можно непосредственно воспользоваться результатами, основанными на использовании подходящей функции угла разращивания /3(г). Конечные формулы для переменной скорости кристаллизации Vc(t) и скорости изменения уровня расплава в тигле Й(1), входящих в выражения m(t) лръ г2 (t)Vc (t) и M (t) - пр R2H (t),
v ,..frpft V.
V рй рзгЧ гЧ Мм МрДОЦР
H(t) - V0 - V0 - (hr1 + h1 fr ) Vctg Д (8) Алгоритм программного задания при переходе к дискретному времени Т0 можно представить следующим рекуррентным расчетом.
На первом шаге принимаем п гз, I 1, k 1 (определение счетчика k дается ниже), на l-том шаге по заданной зависимости /3(г) находим /3i /(n), по известным формулам 4,5 рассчитывают текущую высоту мени- ска: hi(n, ), вычисляют текущую скорость кристаллизацииГУс Vc(n, ), вычисляют очередной радиус кристалла:
П+1-ГЗ+ То У Vcitg #,
длину выросшего кристалла h Т0 2 Vci,
i
текущую массовую скорость кристаллизации MI птг/Э| R Hi, общий прирост взвеши- ваемой массы MI Т0 У Mj, текущую массу
мениска /л пр п г hi (n, ) + пр a2 cos- (Ј+$) вычисляют и запоминают на тз массу выросшего кристалла: (п Mi - fi.
Поскольку в данном способе кристаллизации принципиально важным является определение времени запаздывания тз (т.), зависящего от переменной высоты флюса Hf(t) с известной начальной загрузкой Mf, прежде чем закончить описание расчета программного задания дадим, формулы расчета времени запаздывания.
Для нахождения1 Hf (отсчитывается от фронта кристаллизации) рассмотрим общий объем в тигле известного радиуса R под флюсом (фиг. 1). Поскольку до выхода затравочного кристалла из-под флюса верно соотношение
л (t) + h (t) W, (t) + VMt) +
+ Wfo + W3,(9)
где W fi (t)//oi - объем мениска:
Wmf ITU/PS - объем кристалла, выросшего на величину l(t) / Vc(t) dt;
о
Wfo Mf//9f const - объем флюса;
Wa я - (t) - объем затравки радиуса гз,
находящихся под флюсом, уравнение (9) с учетом условия баланса масс дает
Hf(t)
1
я(Р2гз2)1
мЈ)+Ј11 г Јл
I А/01 L Рь
+ Wfo-Jrr32l(t)- ГС2Ь . (10) -J R - гз
В момент выхода вершины конуса в газовую фазу l(t) Hf(t) и Л/з 0, откуда
н,(,)-1-Г +2 Г1-fi.il jrR2 L L -IJ
+ Hf0-h(t),(11)
+ Hfo - h (t), где Hf0 Mf/jrR2 pi.
Hf (t)
№
С выводом части кристалла из-под флюса (фиг. 1) в (6) необходимо учитывать запомненные ранее рассчитанные значения mtft - Г3):
1 Гм(0-тгЕ-та) ,(0,
tfR2LЛ
j+Hfc-hft).(12)
Таким образом, приняв за начало отсчета момент затравливания, необходимо вычислять и запоминать длину l(t) и массу
растущего кристалла гл J m (t) dt. Если на
о
очередном шаге вычислений выполняется условие i(t) Hf (t), другими словами кристалл начинает выходить из-под флюса, необходимого по запомненным значениям и уравнению (12) восстановить гз (t). Условием правильности определения гз в программном задании (6) является l(t) - l(t - тз) Hf(t).
Продолжим алгоритм рекуррентного расчета программного задания.
Вычисляем толщину флюса Нл:
Нг,а-для Hfi I,- по формуле; (101 Э - для Hfi 1| по формуле: (11) В - для Нп h по формуле (12)
0
5
0
5
0
5
Программное задание до момета выполнения условия, другими словами до выхода конуса из-под флюса, вычисляется по формуле f./ч
Pi g (1 - q) Mi
пр выполнении условия в- по формуле
Р, g(1 )Mi+ g J/mi-k,(13)
где k гз/То
Здесь счетчиком k дискретных отсчетов времени То определяется длина запоминаемого массива данных. Если найденное значение Гз не равно целому числу тактов дискретизации Т0, то в нашем запомненном массиве не нейдется значения m(t - гз|), соответствующего расчитанному времени задержки. Поэтому необходимо найти два ближайших запомненых значения массы кристалла, соответствующих целой части времени запаздывания rail и 1 и далее найти некоторое среднее значение между m ( ) и m ( -1). Способ нахождения среднего в общем случае может быть различен, но в приближении линейного изменения m(t) между соседними тактами дискретизации искомое значение определится как mi (t - гзО (1 - в) m( )+ Е m ), где Ј I li-Hf, ,/VoTo - определяет весовые коэффициенты при вычислении среднего значения m, (t -гзО.
Уравнение (1) определяет структуру реального сигнала весового датчика. Соответ- ственно рассчитанное с помощью приведенных зависимостей нелинейное программное задание (13) должно совпадать с реальным весовым сигналом для мо- метов времени t IT0. При вычитании из реального сигнала весового датчика программного нелинейного сигнала (13) и последующего дифференцирования получают сигнал выходного отклонения, используемый для регулирования текущего диаметра кристалла, с помощью параметрически оптимизируемого PID-регулятора в ходе раз- ращивания до выхода на заданный диаметр кристалла.
Выбор оптимальной структуры и настройки PID-регулятора (в общем случае двухканального) определяется по модели динамики кристаллизации и модели наблюдения при весовом контроле. Математическая модель малой размерности для способа Чохральского с жидкостной герметизацией основана на использовании трех законов сохранения: i) - баланса тепла на фронте кристаллизации, И) - сохранения массы кристаллизуемого вещества и Hi) - сохранения угла роста1
AiGi(t)-AsGs(t)psl-vc(t); M(t) + m(t)+«(t)0; r((t)tg/5(t),
(14)
где A(,Ae - теплопроводности расплава и кристалла;
G|, Gs - градиенты температуры в мениске и кристалле вблизи границы раздела фаз;
PS - плотность твердой фазы;
L - теплота азового перехода;
Vc(t) V0 - H(t) - h(t) - скорость кристаллизации;
M(t), rh (t), /i (t) - скорости изменения масс кристалла, связанного с ним мениска расплава и основной части расплава в тигле соответственно.
f(t) - скорость изменения радиуса кристалла;
/ а - е - угол наклона изотропной боковой поверхности кристалла с вертикалью;
е- угол роста (фиг. 1).
Линеаризация этих трех законов сохранения (14) с учетом переменного угла наклона боковой поверхности кристалла /3 (г) О (фиг. 1) позволяет описать динамику нестационарной кристаллизации системой неавтономных дифференциальных уравнений:
0
д г (t) /Vr (t)J r (t) + An ( h (t)+ + Afi (t) 6 h (t) + A1H (t) д H(t) +Av (t) 6 V0; 5 ft (0 /W (t) 6 r (t) + Аъь (t) д h (t) - -6 H(t) +6V0 (t) + AM (t)dT(t); 0H(t) /Wft)dr(t)+AHr(t)ar(t) + + AHfi(t)(5h(t) + AHV(t)6Vo(t). f15)
В качестве естественных переменных состояния рассматриваются вариации (отклонения) радиуса кристалла д r(t), высоты мениска д h (t) и уровня расплава в тигле д H(t) относительно известных программных значений. Только две переменных состояния xi 5г и xi oh могут быть
5 выбраны в качестве независимых, а б Т #1 и (5 Vi - в качестве компонентов входного вектора возмущений Q(t), так что в матричной записи модель процесса кристаллизации имеет вид
ГхЛ , Гьц 012 wil /ш xaj + Ь21 b22J uuj {16)
или более компактно
X(t) A(t)X(t)+ (B(t) Q(t).(17)
Влияние управления на динамику переходных процессов учитывается добавлением в (17) вектора управления U Ui, имеющего своими компонентами искомые
управления Ut AT(t) и Ua AV0 (t) в Т- и V-каналах обратной связи.
X(t) A(t) X (t) + (В (t) (Q (t) - U(t)) (18) Неавтономная модель малой размерности, определяемая уравнениями (18), характеризует динамику переходных процессов при малых отклонениях от исходного состояния при нестационарной кристаллизации, например при росте начального или конечного конусов. Режим формирования требуемой геометрии кристалла в этом случае можно назвать режимом слежения за нелинейным программным заданием.
Автономная модель процесса кристаллизации с постоянными коэффициентами
ass возникает при исследовании задачи стабилизации диаметра цилиндрического кристалла с исходным круговым сечением радиуса Го. В этом случае наклон боковой поверхности /8 (т.) 0 и стационарная скорость кристаллизации равна VCo V0 - H0(t), где H(t) -ps r02V0/ o R2 -/9s r02); R - радиус тигля. Линейная автономная модель для режима стабилизации запишется
ГхЛ . Гаи аи fxil , fb О 1Гил . .
X2j 312322 X2J 021 D22J UJ2J
или более компактно в виде
X(t) AX(t)+ В u(t).(20)
л
Выходное отклонение Y(t) P(t) - P(t)
может быть представлено в стандартном матричном виде с использованием переменных состояния
Y(t) Yi(t) + Y2(t - гз) CiX(t) + D i Q (t) + + C2X(t - Гз) + D2 Q(t - Тз) (21) Это уравнение является моделью наблюдения при весовом контроле.
Параметрически оптимизируемые PID- регуляторы используют информацию толь- ко об отклонениях выходного сигнала датчика от программного задания. Простота введения интегральных составляющих закона регулирования позволяет обеспечить с помощью подобных регуляторов нужную степень астатизма, запас устойчивости замкнутой системы в обычном способе Чох- ральского, Повышение степени астатизма в первую очередь требуется для обеспечения точного отслеживания нелинейного про- граммного задания в режиме формирования конусов. Очевидно, что задача синтеза управления для обычного способа Чохраль- ского практически совпадает для способа Чохральского с жидкостной герметизацией если формирование конуса происходит полностью под флюсом. В этом случае уравне- ние наблюдения (21) упрощается и определяется в виде
Y(t) Yi(t) Ci(t)X(t)+Di(t)Q(t). (22) В уравнениях (21) и (22) в отличие от обычного способа Чохральского появляется известный заранее множитель (1 - /). При анализе замкнутого состояния вектор входных воздействий Q (t) необходимо заме- нить на вектор Q (т) - U(t) где U(t) - определенный выше вектор управления Вследствие медленного изменения параметров модели (16), (22) при анализе динамики кристаллизации применимо прибли- жение замороженных коэффициентов, позволяющее считать постоянными компоненты матриц за достаточно длительные времена формирования переходных участков кристалла. Переходя к изображениям Лапласа в управлении модели (16) и в уравнении наблюдения (22), получим матричные передаточные функции объекта в замкнутом состоянии;
X(s) (sl-Ay1B Q(s) - U(s) + (sl-Ay O); Y(s) C(sl-A) TB+ (s)-U(s) + + C(s1-A) 1X(0),(23)
где I - единичная матрица (2 2).
Ненулевые начальные условия Х(0) О, а также Q & 0 могут рассматриваться как начальные отклонения (возмущения) и входные возмущения объекта Как и ранее, тепловую инерционность отклика объекта на управляемые изменения мощности нагрева
AN(t) (инерционность температурного Т-ка- налауправления)учтем введением дополни тельной передаточной функции
Ui(s) WT(s)AN(s)(24)
Например, для типичного температурного отклика объекта на ступенчатое изменение мощности Д N(t) AN01(t), аппроксимируемого функцией AT(t) ku АМ0 (1- exp(-at)), где а -декремент затухания, имеет WT(S) aku/(s+a). Далее под управлением ui(t) необходимо рассматривать функцию, задаваемую уравнением (24)
Коррекция тепловой инерционности сводится к введению коротких форсирующих воздействий по мощности нагрева тигля в пределах одного такта управления.
При двухканальном управлении регулирование диаметра выращиваемого монокристалла в ходе разращивания осуществляют посредством управления температурой расплава и скоростью вытягивания монокристалла, причем управляющее воздействие по скорости вытягивания как на стадии разращивания, так и на стадии стабилизации диаметра вырабатывают пропорционально отклонению скорости изменения веса вытягиваемого монокристалла от заданной, не используя в законе регулирования отклонения по весу и второй производной этого измеряемого отклонения по весу. Оптимально настроенный параметрический регулятор позволяет точно воспроизводить заданную геометрию конусной части кристалла и осуществлять без- ударный переход к управлению по состоянию в режиме стабилизации диаметра кристалла.
До окончательного выхода сформированного конуса из-под флюса управление проводится по-прежнему с помощью параметрического регулятора, при этом текущим вариациям геометрии кристалла, характеризуемым величинам д т (t) и dji (t), однозначно связанными с введенными переменными состояния, будут соответствовать известные величины управлений U(t). Возможность запоминания этих величин, исключение ошибки неточного определения программного задания с началом выхода цилиндра из-под флюса, а также постоянство параметров объекта управления позволяют определять его текущее состояние, используемое для расчета управления по этому состоянию.
Синтез управления на стадии стабилизации диаметра основан на использовании эквивалентного наблюдателя типа Люен- бергера, восстанавливащего текущие переменные состояния при одновременном
использовании памяти конечной длины, требуемой для запоминания и последующего использования восстановленных переменных состояния, а также известных управляющих воздействий. Решение зада- чи синтеза оптимального регулятора по состоянию может быть найдено при соблюдении следующих условий: I) - автономная модель, определяемая уравнениями (19), (21), адекватно описывает реальный объект в режиме стабилизации диаметра, II)- имеется точная информация о величине управления, совпадающего на входе в реальный объект и наблюдатель. Второе условие |иожет быть удовлетворено по результатам анализа и коррекции тепловой инерционности объекта, описанных выше.
Рассмотрим также осуществление способа в дискретном времени, реализуемом в управляющей ЭВМ. Для времени дискретиза- ции То в пренебрежении задержкой на съем и обработку информации в ЭВМ дискретная модель процесса представляется в виде
X(k 4-1) ФХМ + f (Q(k)- U(k)),
Y (k) СХ (k) + D (Q (k) - U (k)) + (25)
+ Ci X (k - n) 4- Di () - U (k-n))
где n тз (t)/To;
00
Ф(То) ехр(АТ0) Ј (ATo)Vv;
f(To) (Ф- I)1AB - известные числовые значения для выбранного объекта управления, включающего параметры режимов вы- ращивания и известные константы материала;
I - единичная матрица соответствующей размерности.
Отклонения системы от заданных ста- ционарных условий роста интерпретируются наблюдателем как отклонения начальных условий Х(0) 0 в очередной такт съема информации. При настройке регулятора эти начальные возмущения представляются в классе детерминированных возмущений, аппроксимируемых ступенчатыми функциями X(0)X(k) ConstnpHkT0 t(k-M)T0, .
Эквивалентный наблюдатель представляется следующей системой уравнений:
i(k+1) (k) + fU(k) + уДеГЮ
Y(k) С%) ypU(k)Ч G х (к-тУ+ О и (к-m
Ae(k))-y(K),
л 4(26)
где X(k), Y(k) - восстановленные значения
переменных состояния и наблюдаемой величины:-
0 5-
0
5
0
5
Q 5
0
5
Н - матрица связи объекта с наблюдателем.
Время запаздывания в наблюдателе m не совпадает с реальным временем задержки n и превращается в подстроенный параметр. Учитывая этот факт, ошибку восстановления переменных состояния Дх- (k+1) X (k+1) - X(k+1) следует определять как
AX(k+1) -HC)AX(k)t- HCi(X(k-n) - X(k-m)) + HDi(U(k-n) - U(k-m)) (27). Ошибка восстановления (27) определяется от скорости сходимости наблюдателя без
учета задержки в выходном сигнале lim (
НС) AX(k) 0 и of погрешности, связанной с выбором дискретного времени запаздывания m относительно действительного значения дискретного времени п. Скорость сходимости наблюдателя определяется выбором корней характеристического уравнения
det(zl- Ф+ НС) 0.(28)
По теореме разделения динамика замкнутого состояния определяется набором полюсов характеристического уравнения системы det()det(zl -Ф+ НС) 0. причем искомые матрицы наблюдателя Н и регулятора состояния U(k) -KX(k) могут быть найдены раздельно. Числовые значения матрицы коэффициентов Н находятся заранее из решения уравнения (28). Аналогично оцениваются значения матрицы К, уточняемые далее в процессе эксплуатации регулятора. Восстановленные значения переменных состояния рассчитываются по известным входному U(k) и выходному Y(k) сигналам объекта управления согласно формулеА
Я (k+1) (Ф-НС)Х(Ю + (f-HD)U(k)- -HCiX(k-m)-HDiU(k-m)+ HY(k). x (29)
Анализ ошибки измерения Д е (k) Aei(k) + Ae2(k-m) указывает на необходимость минимизации ее составляющей Д 62(k-m) путем выбора из памяти запомненных значений X(k-m) и U(k-m), причем глубина поиска в массивах X и U может быть различной.
Рассмотрим подробнее определение времени запаздывания m применительно к режиму стабилизации диаметра кристалла.
В ходе стабилизации диаметра монокристалла, вследствие возникающих возмущений кристаллизационного процесса-его форма может изменяться случайным образом и не может быть предсказана заранее, в отличие от режима разращивания, в котором его форма и время запаздывания рассчитываются в соответствии с программным заданием. В предлагаемом способе время
запаздывания гз и, соответственно, связанную с ним запаздывающую составляющую в измеряемом весовом сигнале удается учесть путем использования наблюдателя реального процесса и запоминенных вое- становленных переменных состояния.
В первом приближении время запаздывания после перехода к управлению по состоянию, т.е. после полного выхода конуса из-под флюса, можно оценить по формуле тзо Hfo/Vco, где Hfo - толщина флюса при стационарной кристаллизации строго цилиндрического кристалла диаметром 2г0. Расчетная стационарная высота флюса массой Mr const, полученная из решения систе-
мы двух уравнений Hf0 Hf0 + h0 и /cf1 Mf
тг R 2 Hp - я г2, h0 + я a2 r0 cos к - л r0Hf0 равна
Hfo Mf/яг/Of (R 2 - r0 2) - а2 г0 cos e/(R2 - - r02) - h0 .(30)
В общем случае, с учетом вариаций толщины флюса Hf (фиг. 1,2), отсчитываемой от трехфазной линии до его верхнего уровня д Hf, вызываемых возмущениями объемов мениска д W/ и кристалла д Wc, а также скорости кристаллизации 5 Vc величина времени гз (t) тзо + б гз (t). Вариации высоты флюса о Hf и времени запаздывания дтз в текущей момент времени можно опреде- лить, рассматривая суммарный объем, заключенный между границами расплава и флюса:
W WM + Wmf+ Wf0,(31)
где Np ц/р - текущий объем мениска;
Wmf mf/PS - объем кристалла под флюсом;
Wfo Mf//0f - постоянный физический объем флюса. Поскольку
W - W0 + 5 W(t0) W0 + JlR2(d Hf (to) + + 5h(t0);
VV-VW 3w(to) + PTV 5r(to) + +//hdh(to));(32)
для поправки к фиксированному для данных условий кристаллизации времени запаздывания ГЗО
3Ho)4p((to-)(t0-)(Ы,
°°3(34)
где А2 1/тг Vco (R2- r02).
Уравнение (34) можно переписать, используя переменные состояния xi д г, Х2 д h и управление по скорости вытягивания U2 д V0:
ЈM4H2c,x,(,y2(V)-1TR1 J°U,,
(35)
ГД6С1
- 1I9
C2 pi fih - n R - известные численные значения.
Таким образом, вариация времени запаздывания определяется величинами запоминаемых предыдущих переменных состояния Х(т.о-тз)и управления Ui в случае использования скоростного канала, причем используются восстановленные значения переменных состояния.
Переходя к дискретному времени t Т0, где Т0 - время дискретизации, используемое в цифровой системе управления, можно представить алгоритм вычисления текущего значения гз (I) следующим образом.
Предполагая, что к -тому моменту времени известны значений переменных
состояния и управлений, где (i-1),
необходимо вычислить для некоторого значения k величины
б гз (I) А2 ci Xi (m) + А2 С2 Х2 (т) -л R 2 То
U2
(36)







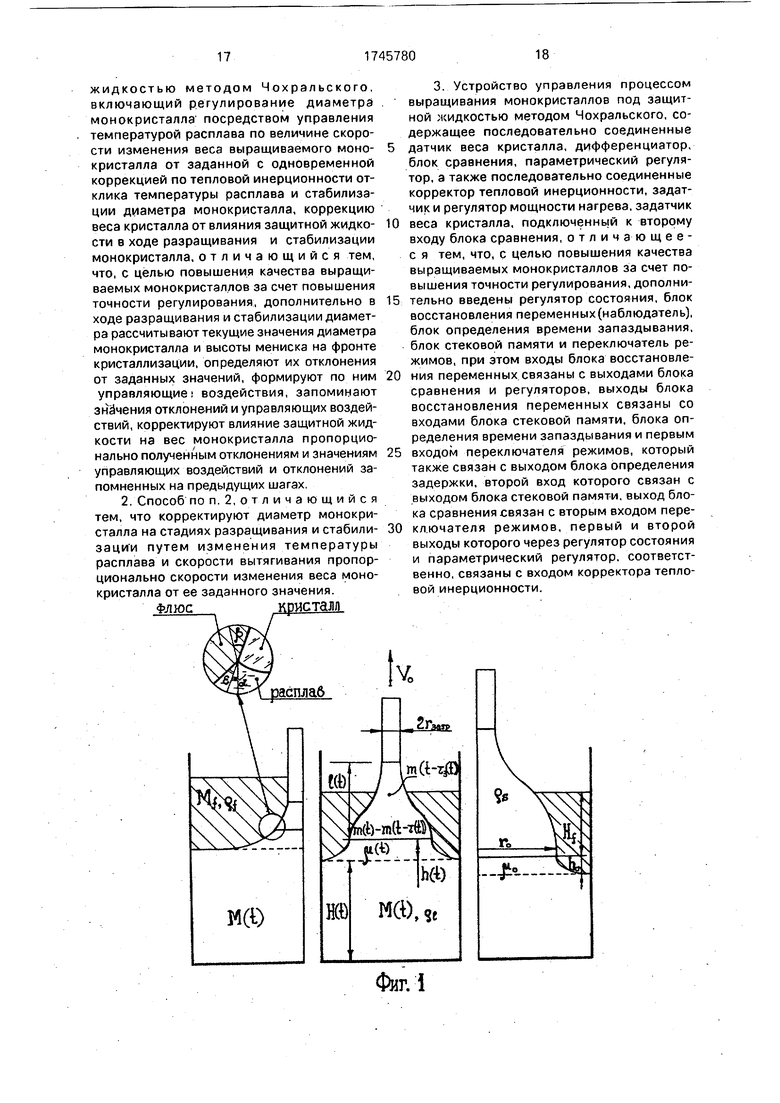
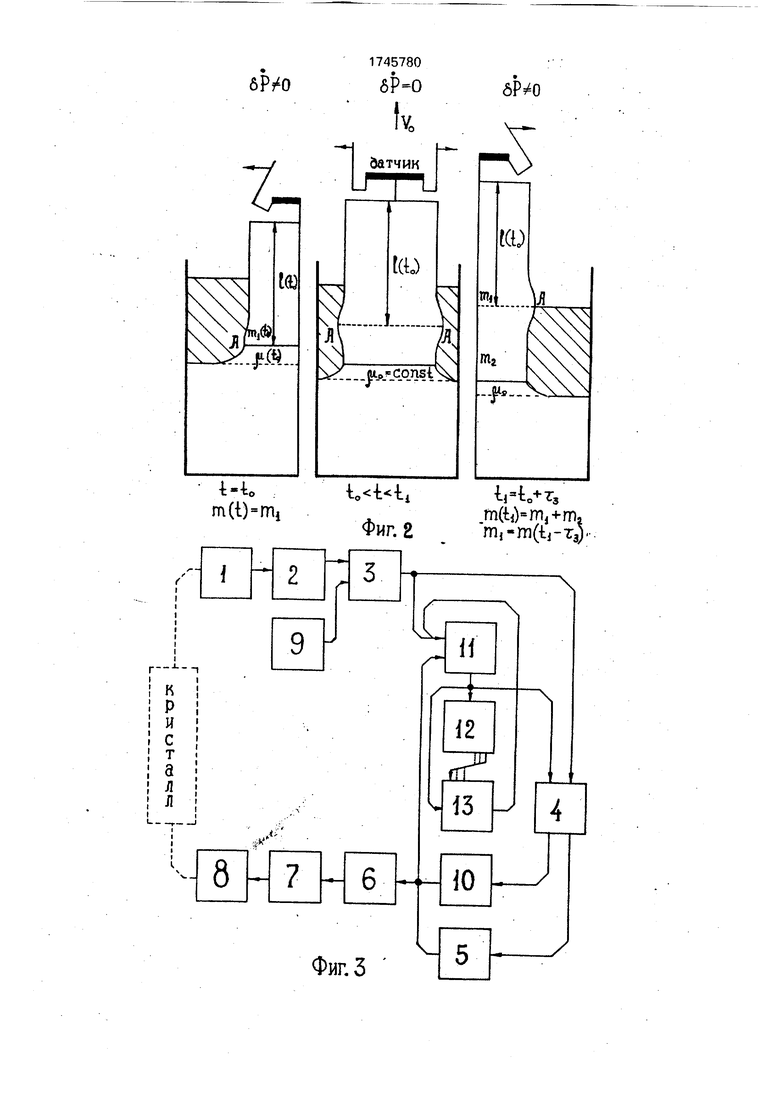
Использование1 изобретение относится к области автоматического выращивания монокристаллов в установках с весовым методом контроля. Сущность: способ состоит в регулировании диаметра выращиваемого Изобретение относится к выращиванию монокристаллов под защитной жидкостью способом Чохральского и может быть использовано для управления процессом кристаллизации на ростовых установках с весовым методом контроля Известны способы, а также устройства управления процессом выращивания монокристаллов под защитной жидкостью методом Чохральского Целью изобретения является улучшение качества выращиваемых монокристалмонокристалла посредством управления температурой расплава и скоростью вытягивания монокристалла по отклонению скорости изменения веса кристалла от заданной величины - на участке разращивания монокристалла, и по состоянию - на участке стабилизации диаметра монокристаллов, для чего используют восстановление переменных состояния с помощью модели процесса кристаллизации и вырабатываемых управляющих воздействий. Кроме того, в ходе всего процесса производится коррекция влияния защитной жидкости на весовой сигнал. Устройство, осуществляющее способ управления, обеспечивает восстановление переменных состояния - радиуса монокристалла и высоты менисча расплава, в наблюдателе Люенборгера, коррекцию влияния защитной жидкости с помощью блока стековой памяти и блока определения задержки, и управление температурой расплава и скоростью вытягивания монокристалла с помощью параметрических регуляторов и регуляторов состояния. 2 с.п. и 1 з.п. ф-лы, 5 ил, лов за счет повышения точности регулирования диаметра. На фиг. 1 представлена схема, поясняющая особенности процесса выращивания монокристаллов под защитной жидкостью методом Чохральского в режиме формирования конуса; на фиг. 2 - то же, в режиме стабилизации диаметра; на фиг. 3 - управляющее устройство, на фиг. 4 - устройство для двухканального управления по температуре и по скорости вытягивания кристалла; на фиг. 5 - функциональная схема блока наблюдателя. 2 СП XI 00 О
О О
Wmt-PeJ ™W XVpsJ W.(t)dt
VЈ
to
+ J A ,
4о-°з
(33)
где to - текущий момент времени измере- ния, причем to тз (to);
Vc Vco + б Vc - переменная скорость кристаллизации.
Из совместного решения (31), (32) нетрудно получить окончательное выражение
0
5
и целую часть от расчетного времени запаздывания
n(k) ((0)/Т0 (37)
В общем случае поиск по k продолжается до тех пор, пока не выполнится условие n m (n+ 1). Очевидно, что этот поиск необходимо осуществлять вблизи значений k i - m0, где m0 тзо/Т0. Уточненные значения переменных состояния в (36) необходимо рассчитывать по формуле
5(i-k) (1 - Б) И (т) + е & (т-1)(38)
где е - вещественный остаток, вычисляемый по формуле (37).
После нахождения очередного значения k необходимость дальнейшего хранения использованных значений переменных состояний и управлений отпадает. Необходимо отметить также, что в случае использования одноканэльного управления по температуре управляемые вариации скорости вытягивания ui 0 и формула (36) упрощаются.
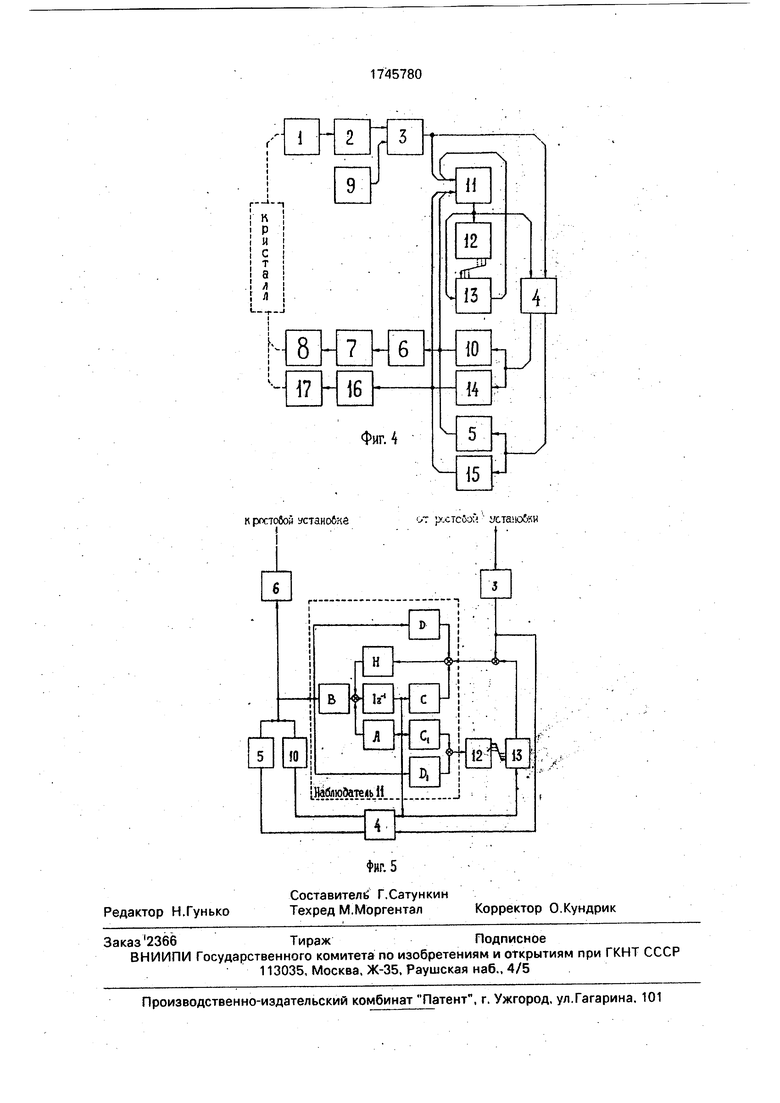
Управляющее устройство содержит последовательно соединенные датчик 1 веса кристалла, дифференциатор 2, блок 3 сравнения, переключатель 4 режимов, параметрический регулятор 5, корректор б тепловой инерционности, задатчик 7 мощности нагрева, нагреватель 8. задатчик 9 веса кристалла, подключенный к второму входу блока сравнения, регулятор 10 состояния, подключенный к второму выходу переключателя режимов параллельно параметрическому регулятору, цепь последовательно соединенных наблюдателя 11, блока 12 стековой памяти, блока 13 определения задержки, причем входы наблюдателя подключены к выходам блока сравнения и регуляторов 5 и 10, а выход дополнительно соединен с вторым входом переключателя 4 режимов и с вторым входом блока определения задержки, выход которого, в свою очередь, подключен к первому входу наблюдателя 11. Кроме того, устройство может содержать дополнительные регулятор 14 состояния параметрический регулятор 15, включенные параллельно регуляторам 5,10. и последовательно с ними соединенные задатчик 16 скорости с управляемым приводом 17 вытягивания, причем выходы регуляторов 14, 15 также связаны с входом наблюдателя 11
Устройство работает следующим образом.
В процессе выращивания датчик 1 веса фиксирует вес кристалла и связанного с ним мениска расплава находящегося вместе с частью кристалла в слое защитной жидкости. Производная сигнала датчика 1 веса, определяемая в дифференциаторе 2, поступает в блок 3 сравнения одновремненно с заданием, формируемым задатчиком 9 веса. Вырабатываемый блоком 3 сравнения сигнал отклонения проходит в наблюдатель 11 и переключатель 4 режимов. По сигналу отклонения и текущемиу управлению, поступающему с выходов регуляторов 5 или 10, наблюдатель 11 восстанавливает текущие значения переменных состояния. В блоке 11 наблюдателя включающем сумматоры, известные матричные элементы А, В, С, D, Ci, Di, H, масштабирующие входные и выходные сигналы а также линию 18 задержки, на один такт основного времени дискретизации сьема выходной информации с ростовой установки (аналог интегратора в непрерывном времени в случае аналогового
исполнения наблюдателя) воспроизводится динамический переходной процесс, соответствующий реальному переходному процессу в ростовой установке. Сигналы, определяемые величинами восстановлен0 ных переменных состояния, совместно с сигналом управления, промасштабирован- ным коэффициентами матрицы Di, поступают на вход блока 12 стековой памяти, где сохраняются необходимое время, опреде5 ляемое количеством разрядов регистров этого блока и тактовой частотой управления. Сигналы с выхода наблюдателя 11 поступают и в блок 13 определения задержки, где формируются сигналы, пропорциональные
0 длине выросшего монокристалла и текущей толщине защитной жидкости. В результате их сравнения определяется разряд регистров блока 12 стековой памяти, в котором содержатся задержанные (запомненные)
5 предыдущие значения переменных состояния и управления, необходимые в данное время для коррекции влияния защитной жидкости. Пропорциональный им сигнал с выхода блока 13 совместно с текущим вы0 ходным сигналом блока 3 поступает на первый вход наблюдателя 11. Скорректированные таким образом сигналы, соответствующие текущим значениям переменных состояния, поступают на второй вход пере5 ключателя 4 режимов. Переключатель 4 режимов передает поступающие на него сигналы отклонения или сигналы, соответствующие текущим переменным состояния, либо на параметрический регулятор 5 либо,
0 по достижении кристаллом заданного диаметра, на регулятор 10 состояния соответственно. Формируемое на выходах регуляторов 5 или 10 управление поступает в наблюдатель 11 для последующего цикла
5 восстановления и в корректор 6 тепловой инерционности, После корректора 6 управление проходит в задатчик 7 мощности нагрева, который соответственно управляющему сигналу изменяет температуру на0 гревателя 8. В ответ на изменение температуры диаметр монокристалла меняется в нужную сторону.
Аналогично осуществляется изменение скорости вытягивания кристалла в устрой5 стве, содержащем дополнительные регуляторы 14, 15, задатчик 16 скорости и управляемый привод 17 вытягивания. Ф о р м у л а и з о б р е т е н и я 1. Способ управления процессом выращивания монокристаллов под защитной
жидкостью методом Чохральского, включающий регулирование диаметра монокристалла посредством управления температурой расплава по величине скорости изменения веса выращиваемого моно- кристалла от заданной с одновременной коррекцией по тепловой инерционности отклика температуры расплава и стабилизации диаметра монокристалла, коррекцию веса кристалла от влияния защитной жидко- сти в ходе разращивания и стабилизации монокристалла, отличающийся тем, что, с целью повышения качества выращиваемых монокристаллов за счет повышения точности регулирования, дополнительно в ходе разращивания и стабилизации диаметра рассчитывают текущие значения диаметра монокристалла и высоты мениска на фронте кристаллизации, определяют их отклонения от заданных значений, формируют по ним управляющие воздействия, запоминают значения отклонений и управляющих воздействий, корректируют влияние защитной жидкости на вес монокристалла пропорционально полученным отклонениям и значениям управляющих воздействий и отклонений запомненных на предыдущих шагах.
Флюскристалл
&РА)
.-, /
1745780
6Р-0
к рогтобой астанобхв
Иаблюаате«ь Н
Редактор Н.Гунько
Фиг. 5
Составители Г.Сатункин Техред М.Моргентал
Заказ 2366
Тираж
ВНИИПИ Государственного комитета по изобретениям и открытиям при ГКНТ СССР 113035, Москва. Ж-35, Раушская наб., 4/5
-Т р .СТСбЭЙ УСТШЮбКИ
А
Корректор О.Кундрик
Подписное

| Riedling К | |||
| Autoromous liquid encapsulated Czochralskl (LEG) growth of single crlstal GaAs by intelligent digital control | |||
| - I | |||
| Cristal Growth, 1988, 89, p | |||
| Способ получения твердых неплавких и нерастворимых продуктов уплотнения формальдегида с фонолами | 1925 |
|
SU435A1 |
| Патент США № 4397813, кл | |||
| Способ обработки медных солей нафтеновых кислот | 1923 |
|
SU30A1 |
Авторы
Даты
1992-07-07—Публикация
1988-11-17—Подача