Изобретение относится к цифровой вычислительной технике и может бьгть использовано в специализированных устройствах цифровой обработки сигналов, работающих в модулярной арифметике, системах счисле- ния остаточных классов или использующих арифметику в полях Галуа.
Известно устройство, предназначенное для йычис лбнШ суммы чисел по моду- лю 2т-1 и соде ржЪщее m элементов НЕРАВНОЗНАЧНОСТЬ, m элементов ИЛИ- НЕ, m элементов И, m элементов ИЛИ, m элементов РАВНОЗНАЧНОСТЬ и соответствующие связи 1.
Наиболее близким по технической сущности и выполняемым функциям к предложенному является арифметическое устройство, реализующее сложение и вычитание чисел и содержащее генератор импульсов, элемент И, регистр первый и второй счетчики, схему сравнения и соответствующие связи 2.
Недостатком указанных технических решений является невозможность суммирования данных по произвольному модулю без изменения структуры устройства, что определяет ограниченные функциональные возможности.
Предлагаемое техническое решение позволяет устранить указанный недостаток и тем самым расширить класс решаемых инженерных задач.
Цель изобретения - расширение функциональных возможностей за счет суммирования данных по произвольному модулю.
Указанная цель достигается тем, что в устройство, содержащее генератор импульсов, первый счетчик, второй счетчик, первую схему сравнения и регистр, причем первый вход (вход запуска сумматора сое- динен с первым входом (входом запуска) генератора импульсов, выход которого соединен с первыми (счетными) входами первого счетчика и второго счетчика, выход первой схемы сравнения соединен со вто- рым входом (входом останова) генератора импульсов, второй вход сумматора (вход первого слагаемого) соединен с третьим (первым информационным) входом первой схемы сравнения, второй (информацион- ный) вход которой соединен с выходом первого счетчика, третий вход (вход второго слагаемого) сумматора соединен со вторым (информационным) входом второго счетчика, введены дополнительно триггер и вто- рая схема сравнения, причем выход генератора импульсов соединен с первым входом (входомразрешения записи) триггера, с первыми входами (входами разреше- iiMfl) первой схемы сравнения и второй
схемы сравнения, выход первой схемы сравнения соединен со вторым входом (входом разрешения записи) регистра, выход которого является выходом сумматора, выход второго счетчика соединен с первым (информационным) входом регистра и со вторым (первым информационным) входом второй схемы сравнения, третий (второй информационный) вход и выход которой соединены соответственно с четвертым входом (входом задания модуля) сумматора и со вторым (информационным) входом триггера, выход которого соеди-нен с третьим входом (входом сброса) второго счетчика.
Суть предлагаемого подхода заключается в реализации оптимальной математической модели вычислений суммы по модулю k в рамках ограничений бинарной элементной базы; критериями оптимальности модели являются количество арифметических и логических операций, а также функция роста операционной сложности при увеличении размерности задачи (параметра значности k).
В основу данного изобретения положены следующие математические модели работы компонентов устройства и их взаимодействия в процессе функционирования.
Под многозначной функцией алгебры логики понимается логическая функция f(xi, Х2,..., хп), аргументы которой определены на
множестве Ek {0, 1-1} и такая, что f(xi.
Х2,..., xn)Ek.
Операция сложения по модулю k представляется в виде многозначной функции алгебры логики f(xi, Х2) xi + Х2 (mod k), где xi и Х2 переменные функции (суммируемые операнды). Любая многозначная функция алгебры логики описывается вектором значений (столбцом таблицы истинности) X х(о), хС1)...„ x(k ;УЗТ. Элементы вектора
хх(о)x(k Ч где х{|)е 6TFT, I - 0, k -T
являются значениями функции на упорядоченных в лексикографическом порядке наборах переменных. Формальное соответствие между элементами вектора значений ли многозначной функцией алгебры логики f(xt, хг) xi + ха (mod k) показано в табл.1.
Теоретически посылки, положенные а основу настоящего изобретения, состоят в следующем.
Для ёектора значений )Г функции f(xi, Х2) xi + Х2 (mod k), интерпретируемого как дискретный сигнал, существует оптимальный базис дискретного преобразования Фурье, который удовлетворяет критериям теоремы Карунена-Лозвз. Матрица преобразования S k в этом базисе формируется по правилу, приведенному, например, в работе Р.Х.Садыхова, П.М.Чеголина, В.П.Шмерко Методы и средства обработки сигналов в дискретных базисах. - Мн.: Наука и техника, 1987.
Sk2
ko.o. ki,o,..., kk-i.(x) Kk ko.1.kl,ikk-l,if®Kk
k-l
t-« k-i
ko.k-1, kl.k-1kk-1,
Л
w
)Kk
где fyj-je K|. Причем (I, j)-u элемент u pnub/Kk 1 формируется следующим
рицы зом:
формируется следующим
где г - второй разряд k-ичного представления параметра I;
xi xi (mod k) при Х2 0, а при Х2 О 5 соответствует циклическому отрицанию переменной xi X2 раз. Операции сложения и умножения в соотношении (5) выполняются в обычной десятичной арифметике.
Вектор спектра Фурье S, полученный в 10 результате преобразования функции f(xi, xa) xi + Х2 (mod k) в базисе S kz, имеет вид:
Г о 1 о о... of.
15 с учетом этого соотношение (5) представляется в виде




| название | год | авторы | номер документа |
|---|---|---|---|
| Модуль для вычисления логических производных | 1989 |
|
SU1730617A1 |
| Устройство для реализации быстрых преобразований в базисах дискретных ортогональных функций | 1985 |
|
SU1292005A1 |
| Устройство для реализации быстрых преобразований в базисах дискретных ортогональных функций | 1983 |
|
SU1115060A1 |
| Устройство для вычисления логических производных многозначных данных | 1990 |
|
SU1837277A1 |
| Устройство для реализации быстрых преобразований | 1986 |
|
SU1416981A1 |
| Устройство для распознавания на линейность булевых функций | 1990 |
|
SU1756879A1 |
| Цифровой обнаружитель-измеритель частоты | 1989 |
|
SU1797127A1 |
| Генератор систем базисных функций Аристова | 1990 |
|
SU1748146A2 |
| Генератор систем базисных функций аристова | 1990 |
|
SU1753465A2 |
| Устройство для вычисления спектра Фурье | 1983 |
|
SU1121678A1 |
Изобретение относится к цифровой вычислительной технике и может быть использовано в специализированных устройствах цифровой обработки сигналов, работающих в модулярной арифметике, системах счисления остаточных классов или использующих арифметику в полях Галуа. Целью изобретения является расширение функциональных возможностей за счет суммирования данных по произвольному модулю. Сумматор содержит счетчики 1,2, схемы сравнения 3, 4, триггер 5, генератор импульсов 6 и регистр 7, 4 ил , Зтабл. у 1 Ё 00 N Ю О 00 -т 1 Результат v суммирования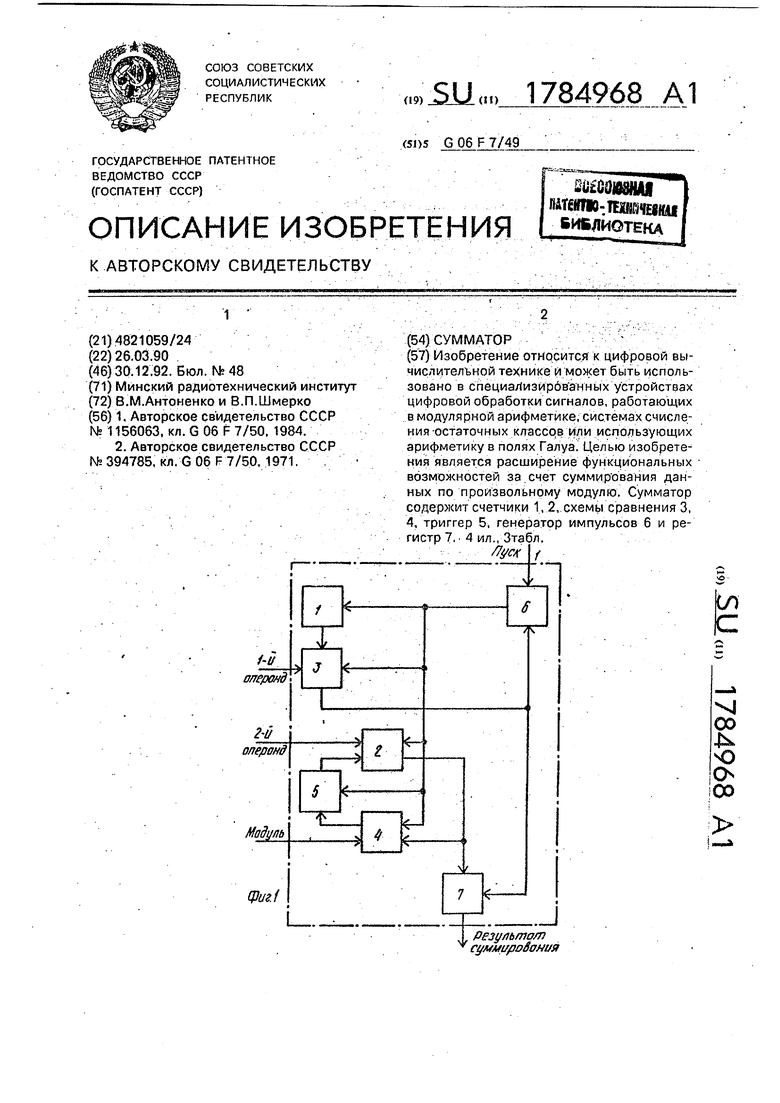
Ь 1 - 1J - (2)
t
где I I (mod k) при t 0, а при t 5 О соответствует циклическому отрицанию параметра 11 раз.
Таблица истинности функции циклического отрицания показана в табл.2. Заметим, что в соотношении (2) операция возведения в степень выполняется в десятичной аоифметике. Значения элементов матрицы Kk определяются из матричного уравнения
(k-1)2 Ik.(3)
л
Kk
где ik - единичная матрица размерности k x k.
Дискретное преобразование Фурье функции f(xi, Х2) xi + Х2 (mod k) в базисе S fez определяется в матричном виде следующим образом:
/
3(1/(k-lf)Sk 5 (4)
где 1/(k-1)2 - нормирующий, множитель, S k - базис дискретного преобразования Фурье, матрица размерности k2 x к2;
Ј S10 5гоS(k 1)T - вектор спектра
Фурье - результат дискретного преобразования Фурье фуНКЦИИ Т(Х1, Х2) Х1 + Х2
(mod k) в базисе S k (фиг.4).
Элементы s 1 (1 0,) вектора спектра Фурье Јf являются коэффициентами арифметико-логической формы (S - формы) представления функции вида:
k2 - 1 г
f(xi.x2) S(X) Ј S(i)Јi,(5)
к2-1 / $ 4
f(xi, х2) - S(X) - 2 S0)1 0x1 1xi + i « о
2Ь-1
X2А2 %
+ Oxi + .,. Oxi xi (mod k),
25
то есть
кг л
f(xi, X2) xi -t- X2 (mod k) xi (mod l), (6)
Изменяя базис дискретного преобразования Фурье в соотношении (4), можно синтезировать множество различных форм представления функции сложения по модулю f(xi, ха) xi + Х2 (mod k). Из множества получаемых решений наиболее приемлема (с точки зрения технической реализации)
S-форма, описываемая соотношением (б), которое является математической моделью .функционирования заявляемого объекта.
Следует заметить, что большинство математических моделей, положенных в
основу функционирования известных устройств, - частные случаи излагаемого подхода.
Поясним суть данного подхода на примере.
Пример. Выполним дискретное преобразование Фурье функции сложения по модулю 3, f(xi, Х2) хуь Х2 (mod 3), заданной вектором значений Г 0 1 2 1 2 0 2 О , в базисе S ka5(/2г)
55
Подставив элементы вектора S в выражение (5), получим
029I
k2 -1 х2 Хг Хг
f(xi,x2) s(x) Ј sfSi-oxi-Mxi +
i Ј X S S
Oxi + Oxi + Oxi + Oxi + OKI + Oxi + Oxi 3).
Матрица S з2 в соответствии с выражением (1) формируется следующим образом:
Зз2
ko.o, ki.o, k2, ko.i,Oki,i,ki.
N,2. kl,2, k2.
Поскольку матрицы Кз (t 0,2), согласно (2) и (3) имеют, вид
200
-3 4-1 1-2 1
002 4-1-3 -2 1 1
020
-1-3 4
1 1 -2
то
40ОООООО О
-6 в-г ооо-оо о
г-4-гоооОо о
-& а ооо -г о g о
Ч Ъ -4 t 3 -4 -и (б -а б -3 г -I - 4 -8
20000204 О -34-4 .( V2 -6 8
4 г -г I г 2 -4
Таким образом, функция f(xi, ха) xi + ха (mod 3) принимает вид
& f(xi, x2)y(mod3).
В справедливости полученного выражения нетрудно убедиться, подставив значения переменных xi и ха. Например, при xi - 1 и Х2 2 получим
Хе 2 л
f(xi, ха) $1 -1 2 - 0 (mod 3),
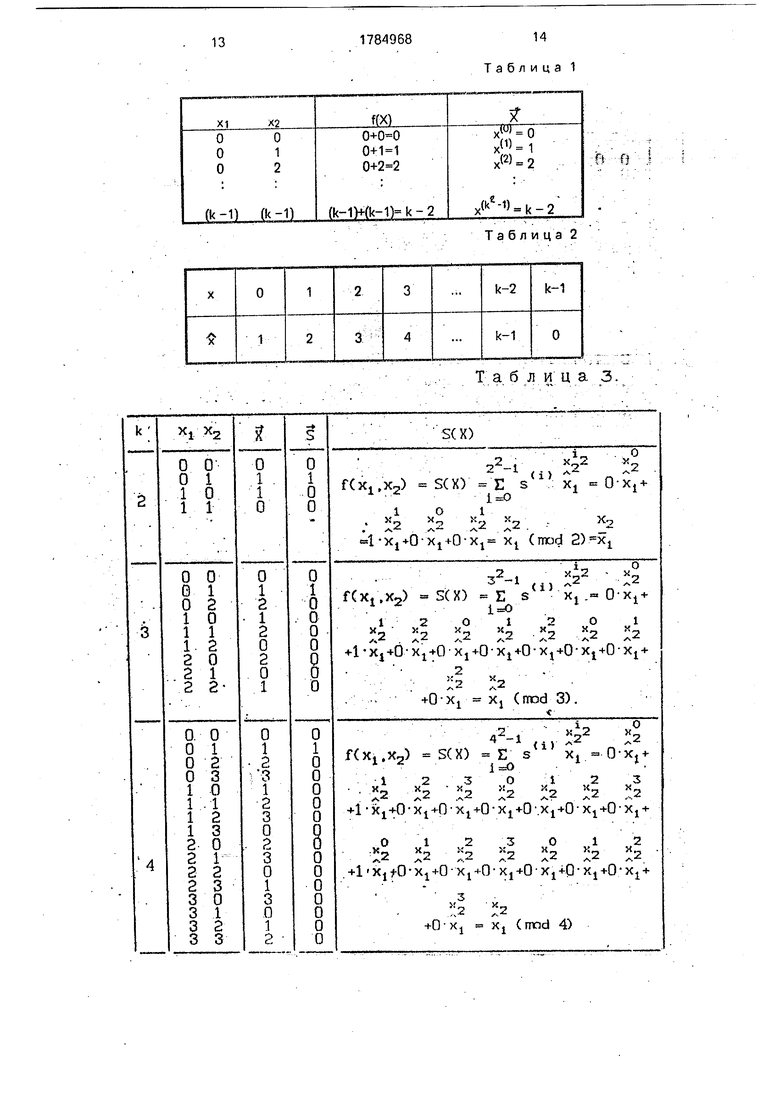
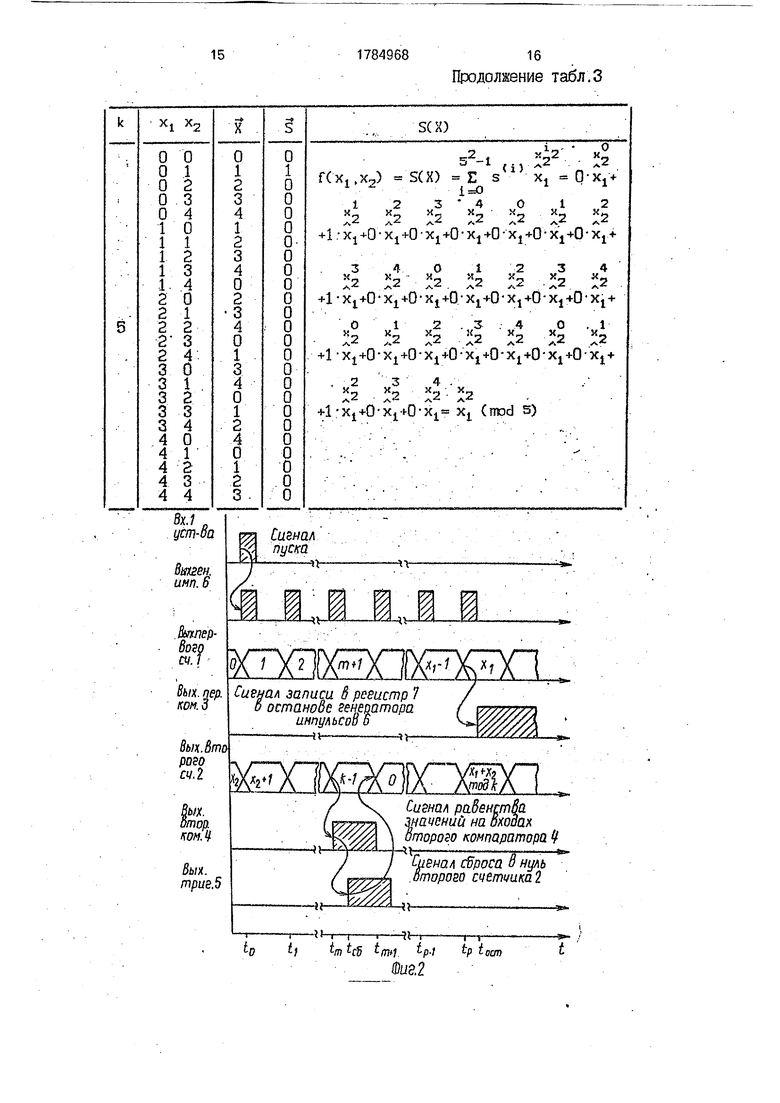
что соответствует значению функции f(xi, ха) xi + Х2 (m&d 3), при xi 1 и Х2 2. В табл.3 показаны векторы значений функции f(xi, ха) xi + Х2(mod k) при k равно м
2, 3, 4 и 5, а также соответствующие им векторы спектров Фурье аналитическое представление исходной функции в виде S- формы.
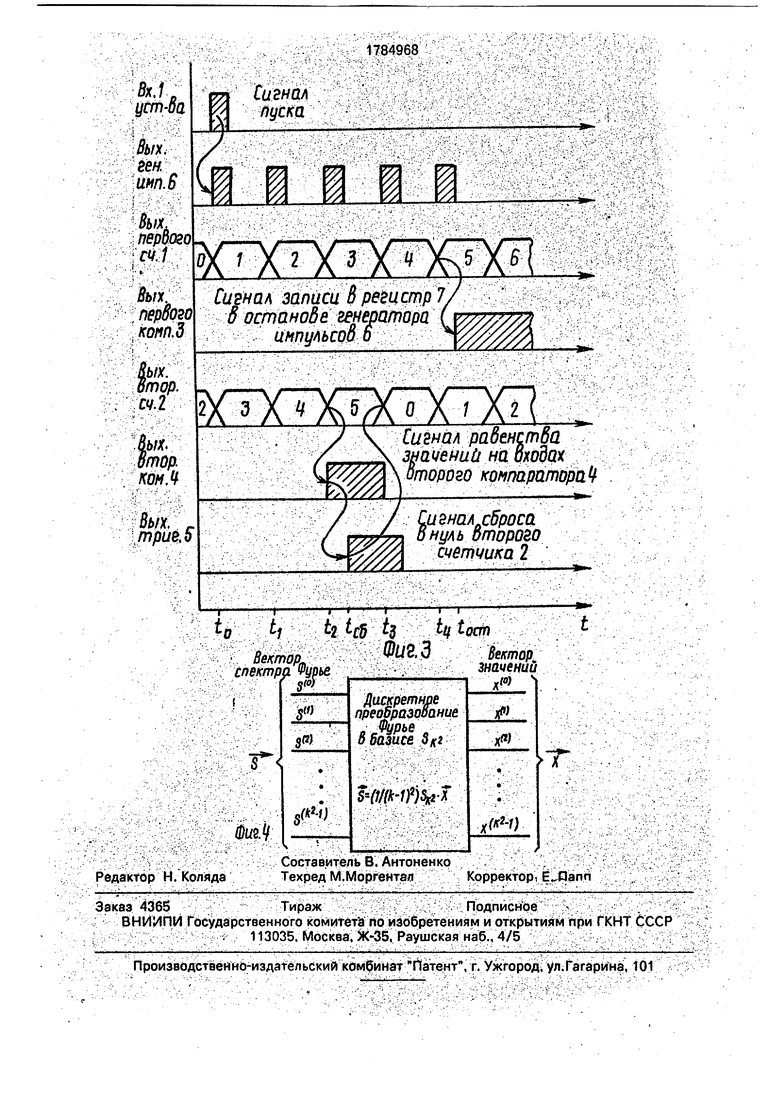
На фиг.1 представлена структурная схема устройства; на фиг.2 - временная диаграмма функционирования устройства; на фиг.З - временная диаграмма функционирования устройства при xi 5, Х2 2 и k 6; на
фиг.4 - обобщенная схема вычисления дискретного преобразования Фурье в базисе
Sk2.
Сумматор по модулю k содержит первый счетчик 1, второй счетчик 2, первую схему сравнения 3, вторую схему сравнения 4, триггер 5, генератор импульсов 6 и регистр 7, выход которого является выходом устройства (выходом результата суммирования), причем первый вход устройства (вход запуска) является первым входом (входом запуска) генератора импульсов 6, выход которого соединен с первыми входами (входами синхронизации) второй схемы сравнения 4, триггера 5, второго счетчика 2,
первой схемы сравнения 3 и первого счетчика 1, информационный выход которого соединен со вторым выходом первой схемы сравнения 3, причем третий вход первой схемы сравнения 3 является вторым входом
устройства (входом первого слагаемого), а выход первой схемы сравнения 3 соединен со вторыми входами (входами управления) генератора импульсов б и регистра 7, первый вход которого подключен к выходу второго счетчика 2 и второму входу второй схемы сравнения 4, причем третий вход второй схемы сравнения 4 является четвертым входом (входом задания модуля) устройс - ва, а выход второй схемы сравнения 4 соо
динен со вторым входом триггера 5, выход которого соединен с третьим входом (входом сброса) второго счетчика 2, второй вход которого является третьим входом устройства (входом второго слагаемого).
Первый счетчик 1 - суммирующий счетчик с коэффициентом счета 2S-1 (S log2k, где - наименьшее целое число, большее или равное ) - предназначен для подсчета числа тактов работы устройства. Первый
вход первого счетчика 1 является суммирующим входом. В качестве первого счетчика 1 может быть использована микросхема К155ИЕ5.
Второй счетчик 2 - суммирующий с ко5 эффициентом счета 2S-1 (S ogak предназначен для формирования результата суммирования. Сброс второго счетчика 2 в состояние 00...02 осуществляется по переднему фронту сигнала на первом входе при
высоком логическом уровне напряжения логическом уровне напряжения на третьем входе. Начальное состояние второго счетчика 2 соответствует двоичному эквиваленту числа ха на его выходе, суммирование осуществляется по переднему фронту сигнала на первом входе. В качестве второго счетчика 2 может быть использована микросхема К155ИЕ7.
Первая схема сравнения 3 предназначена для сравнения двоичных кодов, поступающих на ее первый и второй информационные входы, а также формирования сигналов записи в регистр 7 и останова генератора импульсов б по заднему фронту сигнала на первом входе.
Вторая схема сравнения 4 предназначена для сравнения двоичных кодов, поступающих на ее второй и третий входы, Формирование сигнала на выходе второй схемы сравнения 4 осуществляется при равенстве сигналов на втором и третьем входах по переднему фронту сигнала на первом входе.
В качестве первой схемы сравнения 3 и второй схемы сравнения 4 могут быть использованы микросхемы К555СП1.
Триггер 5 - триггер D-типа - предназначен для формирования сигнала сброса второго счетчика 2 в нулевое состояние. Формирование высокого логического уровня напряжения на выходе триггера осуществляется при высоком уровне напряжения (логической единице) на втором входе по заднему фронту сигнала на первом входе. В качестве триггера 5 может быть использована микросхема К155ТМ2.
Генератор импульсов 6 предназначен для формирования сигналов (прямоугольных импульсов) с постоянным периодом следования, равным одному такту работы устройства. Пуск генератора импульсов 6 осуществляется сигналом на его первом входе, а останов - по переднему фронту сигнала на втором входе. В качестве генератора импульсов 6 может быть использована микросхема К155АГЗ.
Регистр 7 предназначен для хранения результатов вычислений, поступающих на первый информационный вход. Запись в регистр 7 осуществляется по переднему фронту сигнала на втором входе. В качестве регистра 7 может быть использована микросхема К155ИР1.
Сумматор по модулю k в совокупности рассматриваемых компонентов работает следующим образом.
Временная диаграмма работы сумматора показана на фиг.2.
Предварительно первый счетчик 1 и триггер 5 устанавливаются в нулевое состояние; на второй и третий входы устройства подаются соответственно двоичные эквива- 5 ленты первого и второго операндов xi и Х2 (xi k-1. X2 k-1), а на четвертый вход устройства - двоичный эквивалент числа k-1; второй счетчик 2 устанавливается в начальное состояние, соответствующее значению
0 второго операнда Х2 на информационном выходе счетчике.
В момент времени t0 на первый вход сумматора (вход запуска) подается высокий логический уровень напряжения, по пере5 днему фронту которого осуществляется запуск генератора импульсов 6. На выходе генератора импульсов 6 формируется последовательность импульсов, которые поступают на первые входы первого счетчика
0 1, второго счетчика 2, первой схемы сравнения 3, второй схемы сравнения 4 и триггера 5. По переднему фронту импульсов на первых входах (входах суммирования) первого счетчика 1 и второго счетчика 2 осуществля5 ется переключение счетчиков в состояние, соответствующее двоичным эквивалентам значений Qi + 1 и Qa + 1 соответственно на информационных выходах счетчиков (Ch и Оз - предыдущие значения на информэци0 онных выходах первого и второго счетчиков соответственно).
В момент времени tm (m xi - 1) когда на информационном выходе второго счетчика 2 формируется двоичный эквивалент
5 числа k-1 (фиг.2), на выходе второй схемы сравнения 4 формируется высокий логический уровень напряжения. В результате этого по заднему фронту импульса на первом входе триггера 5 в момент времени tC5 на
0. выходе триггера 5 формируется высокий логический уровень напряжения, который поступает на третий вход (вход сброса) второго счетчика 2.
В момент времени tm+i по переднему
5 фронту импульса на первом входе второго счетчика 2 происходит переключение второго счетчика 2 в состояние 00...02.
Функционирование устройства с момента времени tm+2 по tp (р xt - 1) анало0 гично его функционированию с момента
времени t0 по tm. .
В момент времени tp, когда на выходе
первого счетчика 1 формируется двоичный
эквивалент числа XL на выходе первой схе5 мы сравнения 3 формируется высокий логический уровень напряжения, являющийся признаком конца работы устройства, по переднему фронту которого в моменту времени toci осуществляется запись информации
(значения xi + Х2 (mod k)) в регистр 7 и останов генератора импульсов б.
Таким образом, на выходе устройства (выходе результата суммирования) формируется результат вычислений - значение xi + Х2 (mod k). Рассмотрим работу устройства при вычислении суммы по модулю k 6 значений xi 5 и Х2 2 в соответствии с математической моделью (6).
Временная диаграмма функционирования устройства для данного случая показана на фиг.З.
Предварительно первый счетчик 1 и триггер 5 устанавливаются в нулевое состояние; на второй и третий входы устройства подаются значения хч 5 и ха 2 (в двоичных кодах) соответственно, а на четвертый вход устройства - двоичный эквивалент числа k - 1 5; второй счетчик 2 устанавливается в состояние, соответствующее двоичному эквиваленту числа ха 2 (0. 01 Оа) на информационном выходе.
После пуска генератора импульсов б. по переднему фронту импульсов на первых входах первого счетчика 1 и второго счетчика 2, на выходах счетчиков формируются двоичные эквиваленты значений 1 (О.„012)и Х2 + 1 - 3 (0...0112) (в момент времени to), 2 (0.. ОЮз) и ха + 2 4 (0.. 01002) (в момент времени ti).
В момент времени ta на информационных выходах первого счетчика 1 и второго счетчика 2 формируются двоичные эквиваленты значений 3 (0...0112) и Х2 + 3 5 к-1 (0...01012). В результате это го на выходе второй схемы сравнения 4 формируется высокий логический уровень напряжения, поступающий на второй вход триггера 5. По заднему фронту импульса на первом входе триггера в момент времени tee (фиг.З) на выходе триггера формируется высокий уровень напряжения (логическая единица), который поступает на третий вход (вход сброса) второго счетчика 2.
В момент времени ta no переднему фронту импульса на первом входе второй счетчик 2 переключается в состояние 0...002 (Ою). а первый счетчик 1 - в состояние 0...01002 (4io). Поскольку в момент времени t4 на выходе первого счетчика 1 формируется двоичный эквивалент числа 5 xt (0...0101з). на выходе первой схемы сравнения 3 по заднему фронту импульса на ее первом входе формируется высокий логический уровень напряжения, по переднему фронту которого происходит останов генератора импульсов 6 и запись значения xi + Х2 1 (mod б) (0...012). сформировавшегося на информационном выходе второго счетчика 2, в регистр 7. В результате этого на выходе устройства в момент времени tocr
формируется значение xi + Х2 1 (mod 6).
Таким образом, предлагаемое техническое решение обеспечивает расширение функциональных возможностей за счет суммирования данных по произвольному модулю, что позволяет расширить класс решаемых задач.
Ф о р м у л а и з о б р ете н и я Сумматор, содержащий генератор импульсов, первый и второй счетчики, первую
.схему сравнения и регистр, причем вход запуска сумматора соединен с входом запуска генератора импульсов, выход которого соединен со счетными входами первого и второго счетчиков, выход первой схемы
сравнения соединен с. входом останова генератора импульсов, вход первого слагаемого сумматора соединен с первым информационным входом первой схемы сравнения, второй информационный вход
которой соединен с выходом первого счетчика, вход второго слагаемого сумматора соединен с информационным входом второго счетчика, отличающийся тем, что, с целью расширения функциональных возможностей за счет суммирования по произвольному модулю, он содержит триггер и вторую схему сравнения, причем выход генератора импульсов соединен с входом разрешения записи триггера, с входами
разрешения первой и второй схем сравнения, выход первой схемы сравнения соединен с входом разрешения записи регистра, выход которого является выходом сумматора, выход второго счетчика соединен с информационным входом регистра и с первым информационным входом второй схему сравнения, второй информационный вход и выход которой соединены соответственно с входом задания модуля сумматора и с информационным входом триггера, выход которого соединен с входом сброса второго счетчика.
«о
rr
5 с; Ю
т
х со о ч- со г15
178496816
Продолжение табл.3
Шпал fiytKpi
2
Сигнал записи В 7,
8 оста нодё генератора п :;.; : импулъсъ&и
ЫХ.
faop.
ш
2
bit
шр. ком Л
ГШ с
триъ,$
o ti k ttf Ј3 ttfiocfri
ВехтоьФЧЪЭ
спектра щвье
S(0
...,. , :. .
№
pemi преббраювание «.Фурье а В базисе Зкг
зна
з®
5
S
О
/ Л 2
Сигнал равенства значений нц мода Второго крипаратора.
Сиёнал.сброса о нуль второго счетчика 2
Вектор значений
м
Ж
хУ
Т
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Сумматор по модулю 2 @ -1 | 1984 |
|
SU1156063A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО | 0 |
|
SU394785A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| операнд операнд Модуль фиг( | |||
Авторы
Даты
1992-12-30—Публикация
1990-03-26—Подача