синхронизации блока задержки и второго, третьего и четвертого регистров памяти, второй делитель, первый вход которого соединен с выходом счетчика импульсов, второй вход соединен со вторыми входами первого делителя и блока сравнения и является входом коэффициента деления, третий сумматор, выход которого является выходом цифрового нерекурсивного фильтра, а также первый, второй, третий и четвертый вычислительные блоки, первые входы которых соединены с выходом второго делителя, вторые входы соединены соответственно с выходом первого сумматора, второго регистра памяти, третьего регистра памяти и четвертого регистра памяти, а выходы соединены с соответствующими входами третьего сумматора..
Принцип работы предлагаемого цифрового нерекурсивного фильтра основан на предварительном группировании отсчетов, осуществляемом с помощью второго сумматора и первого регистра памяти. Последующая обработка цифрового сигнала сводится к цифровой фильтрации с последующей квадратичной интерполяцией по четырем узлам, причем предварительное группирование от- счетов.создает тот же эффект, что и увеличение числа звеньев в фильтре прототипа, а изменение числа предварительно группируемых отсчетов (Nrp) позволяет электронным путем управлять интервалом памяти предлагаемого устройства, кроме того в предлагаемом устройстве при операции цифровой фильтрации в блоке умножителей используются весовые блока, имеющие общий вход задания коэффициента умножения (индивидуального для каждого весового блока), благодаря этому обеспечивается управление формой весовой функции в процессе работы цифрового i нерекурсивного) фильтра. Используемая в цифровом нерекурсивном фильтре операция квадратичной интерполяции позволяет восстановить частоту следования отсчетов сигнала, до исходной (т.е. той, что была на входе), причем с целью увеличения точности квадратичная интерполяция осуществляется по четырем узловым точкам с помощью второго, третьего, четвертого регистров памяти, второго делителя, первого, второго, третьего и четвертого вычислительных блоков и третьего сумматора, счетчик импульсов и блок сравнения, используются для синхронизации цирфового нерекурсивного,фильтра.
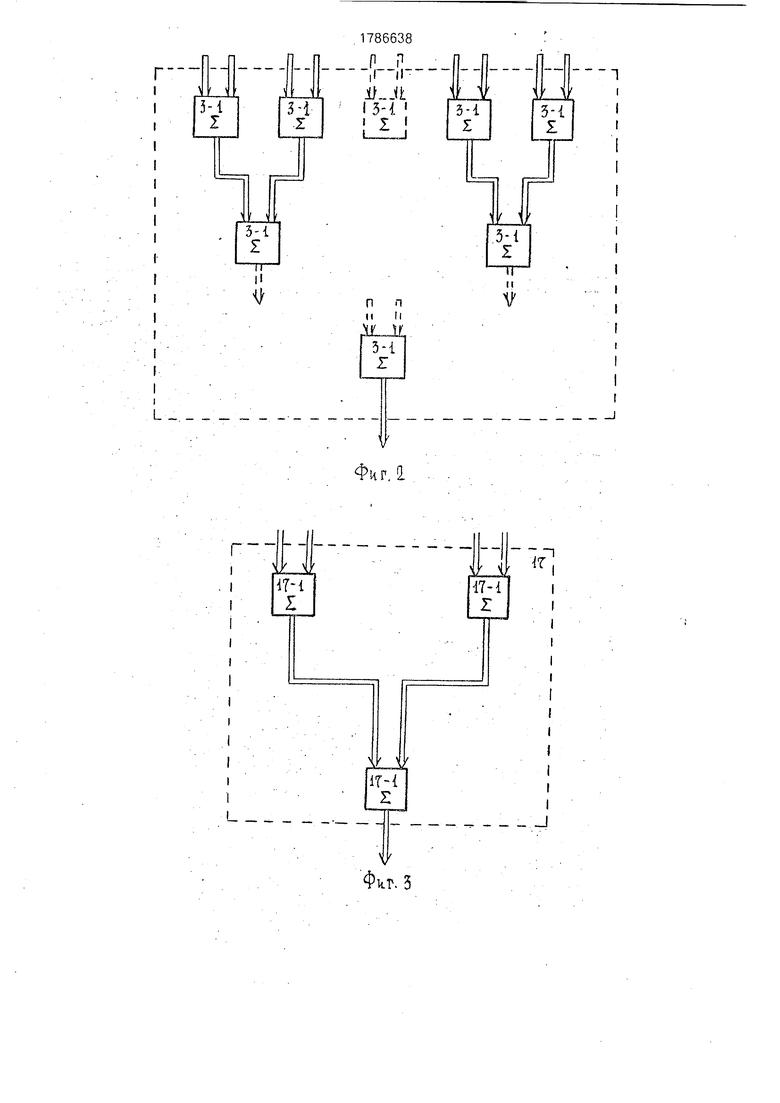
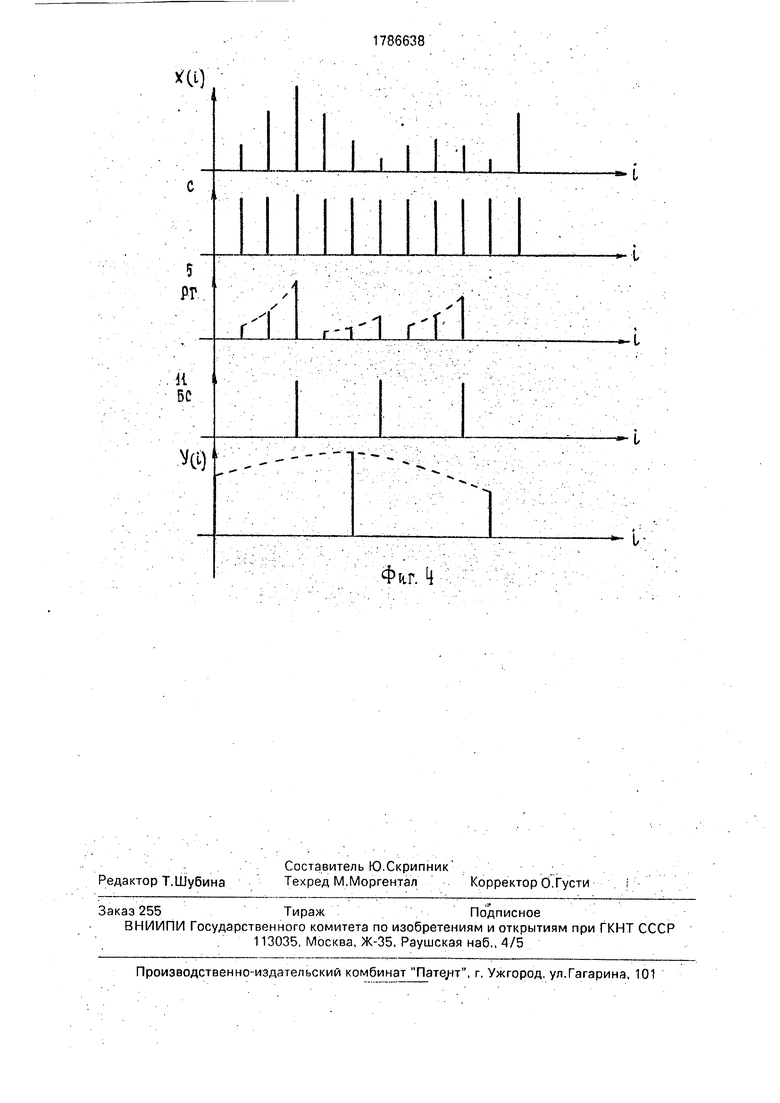
Сущность изобретения поясняется чертежами, где на фиг.1 показана структурная схема цифрового нерекурсивного фильтра, на фиг.2 показана структурная схема первого сумматора, на фиг.З показана
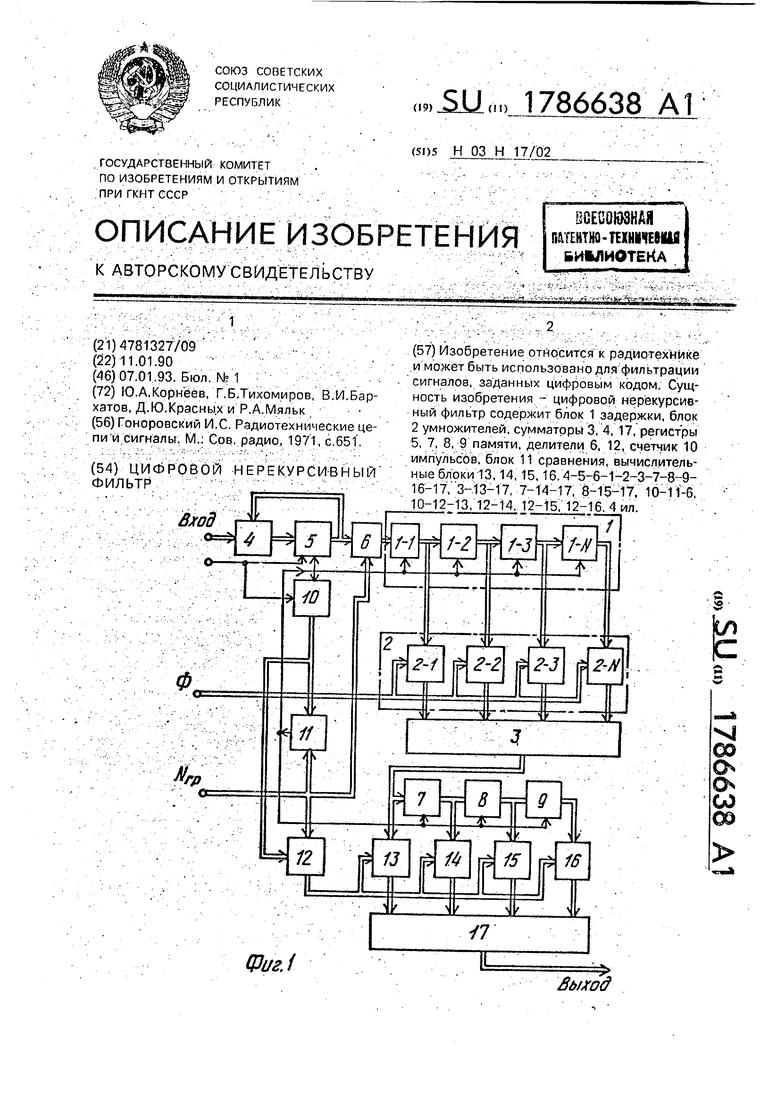
структурная схема третьего сумматора: на фиг.4 показаны диаграммы работы цифрового нерекурсивного фильтра. Многоразрядные связи обозначены двойными линиями, одноразрядные - одинарными. 5Цифровой нерекурсивный фильтр (фиг. 1) содержит:
1 - блок задержки, состоящий из регистров памяти 1-1,..., 1-N;
2 - блок умножителей, состоящий весо- 0 вых блоков 2-1,..„2-N;
3 - первый сумматор;
4 - второй сумматор; . 5 - первый регистр памяти;.
6 - первый делитель; 5 7 - второй регистр памяти;
8 - третий регистр памяти;
9 - четвертый регистр памяти;
10 - счетчик импульсов;
11 - блок сравнения; 012 - второй делитель,
13 - первый вычислительный блок;
14 - второй вычислительный блок; 15-третий вычислительный блок; 16 - четвертый вычислительный блок; 5 17 - третий сумматор.
Первый сумматор (фиг.2) содержит кас- кадно соединенные двухвходовые суммато-.
ры. - , ...: . . .
Третий сумматор (фиг.З) содержит три 0 двухвходовыхрумматора.
На фиг.4 приняты следующие обозначе-:, ния: - . , ::-h-V;
x(i)-дискретный сигнал, подаваемый на вход цифрового нерекурсивого фильтра; 5 с-синхросйгналы, подаваемые насййХ- ровход цифрового нерекурсивного фильтра ; 5РГ - сигналы на выходе первого регистра памяти 5; - .. - ;; -..
11БС - сигналы на выходе блока срав- 0 нения 11;.
y(i) - сигналы на выходе первого сумматора 3.
Цифровой нерекурсивный фильтр содержит первый регистр памяти 5, последо-4 0 вательно соединенные блок задержки 1, блок умножителей 2, второй вход которого является входом задания коэффициентов умножения (весовой функции фильтра), и : первый сумматор 3, а также последователь- но соединенные второй 7, третий 8 и четвер- 5 тый 9 регистры памяти, а также второй сумматор 4, первый вход которого является ; информационным входом цифрового нерекурсивного фильтра, а выход - соединен с информационным входом первого 5 регистра памяти, первый делитель 6, первый вход . которого соединён с выходом первого 5 регистра памяти и со вторым входом второго 4 сумматора, а выход соединен с информаионным входом блока задержки, последоательно соединенные счетчик 10 импульов, информационный вход которогоо оединен с входом синхронизации первого регистра памяти и является тактовым вхр- ом цифрового нерекурсивного фильтра и блок 11 сравнения, выход которого сбедм- нен с входом установки в ноль счетчика им-: пульсов 10 и первого 5 регистра памяти и с входами синхронизации блока задержки и второго 7; третьего 8, и четвёртого 9 рёгист- ров памяти, второй.12 делитель, первый вход которого соединен свыходомi счетчика импульсов 10, второй вход соединен Со BTOL рыми входами первого 6 делителя и блока 11 сравнения и я вл яетЬя входов к6д:Ффици- ёнта деления (группировагйия), третий 17 су мма тор,; выход которого является; выходомцифрового нерекурсивнРгб фильтра, а также первый 13, второй 14, третий 15 . и четвертый .16 вычислительные блоки, пер вые входы которых соединены.-f с выходом втором 12 делителя; вторые ixoflbi СоедйнеИ ны соответственное выходом первого3 сумматора, Ёторого 7, третьего 8 и четвертого 9 регистра, памяти, а выходы соединены с со- Ьтветствующими входами третьего 17 сум - матора, - -.;- -:/;/1 1..,:-. : : - - .. , : .-... .,
, Блок умножителей 2 состоит из весовых блоков 2-1,...,2-N, которые реализуются на интегральных цифровых .микросхемах постоя иных запоминающих устройств (ПЗУ). В этом случае первымУвёсового блока 2-1 явля- ется первая часть; адресных вхШов сЬответ- ствующей .ему микросхемы ПЗУ, вторым - управляющим входом весового блока 2-i является вторая часть адресных входов этой микросхемы ПЗУ, а выходом весового блока 2-1 являются информационные выходы этой микросхемы ПЗУ, причем коды, записанные в ПЗУ блока умножителей 2 определяются, пользователем в соответствий с требуемой весовой функцией, а таблица истинности ПЗУ расчитывается в соответствии с трёбу- емойвёс овой функций, а таблица истинности ПЗУ расчитЙёается в соответствии с выражением: :.. : :: - . ...., л -- .; : ; (birA2.A1 У (А2,)))У .(1) где А1 - число, подаваемое на первую часть (младщих) адресных входов ПЗУ (первый вход весового блкоа 2-I); А2 - число, подаваемое на вторую часть (старших) адресных входов ПЗУ (второй вход весового блока 2- I); Р(А1) - разрядность числа (двоичного), подаваемого на первый вход весового блока 2-I; значение записываемого веса, определяемого числом, подаваемым на второй вход весового блока 2-I, причем ,,,,N; N - число регистров памяти 1-k; ent - операция округления до целого числа; V -.
операциия логического ИЛИ, . - операция арифметического умножения; D-число,
снимаемое с информационного,выхода ПЗУ (выход весового блока 2-1); 5 Пример расчёта таблицы истинности.
Допустим разрядность числа, подавае- могЬ на первый вход весового блока 2-1 . Р(А1)8, разрядность 4исла, подаваемого на второй вхЬд весовргб,блока 2-Г Р(А2)5, тог- 10 да в соответствий с формулой (1) таблица : истинности рассчиты вается следующим об pS30f :: ±: : ; ;
: ; В да н н ой та бл и Цё все в ел йч и н ы за п и с а - |Ы в шестнадцатйричнбм виде, прмчем зна- 15 чения Ь1,А2 ;;-А задаётс пользрвателем. в Г соот в ётст вии с требуемой в ёс.рв.ой.. ; цией цифрового нере1курсйвнЬго фильтра. ; , Первый дёлитёль;б реализуется не пО- стоян;ном апо;ми а ю щём стр рй твё и 0 представляет собой управляемый арифме-:
: тический делители, причем на первую часть
; адресных входов ПЗУ (первый;вхоД первого делителя 6) подается входная информация (число), а наг вторую: Часть адресных входов 25 ПЗУ (второй вход делителя б) подаётся уп- .. : равляющая информация (второй число) и с . информациоййых выходов ПЗУ снимается ; /выходная информ ацйй; причем таблица ис- :; тинности всбответствйи с выражением: 30 .-.- -i . - (2) ..;.
::: А1 - ч ислб,;П:6йав аГёмое на первую часть адресных входов ПЗУ (первый вход пёрвбгр; : делителя б); Яуу;; : ;г д-:: :;Д :. .; :: А2 - чйс лб, подаваемое на itbpyto часть 35 адресных входов ПЗУ (второй вход первого
делителя.6); : - ;$ -i: ; .--. ; ent - one рация округления до целого
:л .чй сла; -..-/ 1:: -.;
.. - операциҐ арйфмётйчес кого умно40 ЖёНИЯ; :;;::%.;.:; Д ; / :..; :/ 1 .- /:: . :; . ;
р - ;число, снимаемое с информационного выхода ПЗУ (выход первого делителя
fi -..-.- - .. . .... .. . .- -. - -. : .fy - V V VV: .- - ..-....: :.-. ; .... ;, Расчёт таблицы истинности осущёств- 45 ляётся аналЬгйчйо вышеприведенному niDH
;;: Дм ёр У ; : ; ; Используемый второй делитель. 12 и вычислительные блоки 13-16 реализуются на интегральных цифрйвьгхмикросхемах ПЗУ и 50 служат в описываемом цифровом нерекурсивном фильтре для вычисления специальных функций вида: ; .
(A1,A2), .. (3) . где А 1 - число, подаваемое на первую часть 55 адресных входов ПЗУ (первый вход блока
ПЗУ); :: ;: . . . :
А24- число; подаваемое на вторую часть адресных входов ПЗУ (второй вход блока ПЗУ);.
f - символ специальной функции;
D - число, снимаемое с информационного выхода ПЗУ )выход блока ПЗУ).
В описываемом цифровом нерекурсивном фильтре используются блоки ПЗУ, в которых записаны следующие «оды: второй делитель 12.
(A1 /A2) вычислительный блок 13
(A1.A2.(A2-1)/4) :вычислительный блок 14.
.. (A1.A2.(A2-5)/4j, . вычислительный блок 15
. (А1 .(А2-1).(А2+4)/4), вычислительный блок 16
D-ent(A1.A2.(A2-1)/4), ....(8) где А1.- число, подаваемое на первый вход вычислительного блока; ;. . -А2 -.число, подаваемое на второй вход вычислительного блока; .... :
ent-- операция округлетя до целого числа; .
... .;- D - число, снимаемое с выхода вычислительного блока, . .... v . : Разрядность At, А2, D определяется разрядностью входных/данных, поступаю- щих на первый вход второго Сумматора 4 и
.разрядностью управляющих данных, поступающих на второй вход блока сравнения 11. . Все остальные блоки цифрового нерекурсивного фильтра реализуются на. интегральных цифровых микросхемах серий К155 и К555 в стандартном включении..Устройство работает следующим обра зом. На вход устройства подается дискретный цифровой сигнал x(i) (фиг.4), каждый отсчет которого сопровождается синхроимпульсом с (фиг.4). Входной сигнал подается
на первый вход второго сумматора 4, который совместно с первым регистром памяти 5 осуществляется накапливающее суммиро- вание; поступающего сигнала в цифровом виде. Процессшкапливающего суммирования состоит в последовательном суммировании ряда отсчетов с последующим обнулением и повторением указанной п ро- цёдуры (эпюра 5РГ на фиг.4). Количество
группируемых отсчетов задается кодов Nrp, который, подается на второй вход блока сравнения 11. Счетчик импульсов 10, совместно с блоком сравнения 11, образует счетчик с переменным коэффициентом деления входных синхроимпульсов с, причем на выходе блока сравнения 11 формируется импульс 11 БС (фиг.4). Когда код 1МГр совпадает с текущим кодом на выходе счетчика 10
(фиг.4), изменяющего свое состояние на +1 с приходом каждого синхроимпульса, им - пульс с выхода блока сравнения 11 обнуляет счетчик 10 и первый регистр памяти 5 (эпю- 5 ра 5 РГ на фиг,4). Первый делитель б выполняет функцию номиров кй сйгна7}а (кода), поступающего на его первый вход, причем нормирующей величиной является код величины Nrp, поступающий на. второй вход
10 первого делителя 6, Работа первого делителя 6 описывается формулой (2). С выхода первого делителя 6 сигнал поступает на информационный-вход блока задержки Т и записывается в-него импульсом 11БС(фиг.4)с
15 выхода блока сравнения 11.Блок задержки представляет собой цепочку последовательно соединенных регистров памяти 1-i, первый вход которых является информационным, а второй вход - синхррв20 ходом. Импульсы, поступающие с выхода блока сравнения 11 на синхровход блока задержки обеспечивают продвижение информации со входа каждого регистра памяти 1-i на его выход, благодаря чему
25 обеспечивается одновременное получение
последова тёльН ости задёржэ ннь х друКЬтносителько друга на один такт отсчетов.
Каждый из задержанных отсчетов домножз:
ется на соответствующий песрвой множи30 тель в весовых блоках, ,.2-j . блока умножителей 2. Полученные задержанные Ътсчет ы, дбмйожённые н а соотв етствую щие весовые множители суммируются в первом сумматоре 3. Таким образом, для нерекур35 сивного фильтра сигнал, поступающий на.
, вход регистра 1-2 блока задержки 1 и сигнал, снимаемый с выхода первого сумматора 3, связаны выражением:
yi(nT)
;
bi х1((п-)Т),
(9)
где х1(пТ) - сигнал, подаваемый на вход регистры 1-2 блока задержки 1, bj -значения весовых коэффициентов, записанных в соответствующие весовые блоки 2-j;
у1(пТ) - сигнал, на выходе первого сум- матора 3. . ....
Весовая функция нерекурсивного фильтра описывается выражением:
V(i
пт) i t
bi.1((n-|).T),
55f 1. (10) где1(п-1) .
(0, п±
х1(пТ) - это сигнал на выходе регистра группирования 1-1, полученный путем труп(11)
(12)
пирования Nrp - отсчетов входного сигнала (x(nT)j (поступающего на первый вход второго сумматора 4) с последующей нормировкой в первом делителе 6, и фиксацией в регистре группирования .1-1, описываемый следующим выражением:
Nrp - 1 I- : -
x1(nT) x(Nrp.iH-k); или
.- k о .. :;. ..-
:.- Nrp-v --: : : -:;:
х1((п-1)Т Ј x((Nrp(n-l)+k)T,
у ;..;;.; -.,.;..:. ... k о .: . . : . .;.;., , . ;-.л;::- ... :,,,где Nrp - группируемое число входных отсчетов (задается на втором входе блока сравнения 11) ;:;; ;; /;.,/. - .. ;.-....
I .-номер регистра памяти 1-1 блока задержки 1,...-.:..,л;-.; С:: . - :. - . ; Ы - весовой коэффициент; : -:. :: ,-г
Тогда, подставляя (12) и (9) получим: ;.-,;N Nrp -I - .;.-,; :.:;-:.;-.
..: . Yl(nT) Ј bi( 2 x ((NrP (n-l)+K)Tfe
: . ; , . 1 . ,. к - о.; :., :, ... . (P)
Пояснить физический . формулы (13) можно следующим образом. ;j ;- .;:-;
Допусти .м. , тогда-формула 25 (1 3) станбв йгся аналогичной фор- ч : муле (9), интервал памяти ц ифрЬг О вбгр нерекурсивного фильтра будет равен N, где N - Число регистров памяти 1-i циф-у рового нерекурсивного фильтра, а вёЬЬвая 30 функция будет описываться формулой (10). Допустим , тогда формула (13) примет ид;:;:; -; ;у -::; ;::0;.
/о укпт) | ь, fi -iff :1 i3fi ; ti4
а весовая функция будет описываться выр а- : жёниё м: ,:: л- -.:i-i : у ..; .:. :::,, . . V.:.
V(nT) | b,lp(n-l)T)+1((2(ri-l)+1)T), ;40
. fi, -. :-- : :f ..: :- :. - где 1(2(n-l)T)y ;;;; V : ; ч Л : Г /
-.;..:.:- V. (o,n/). ;V; :;-;rV;;; -;::/lv- ; г;
Это значит, что протяженность, весовой 45 функции V(nT) и, ел ёдб вётел ь но , интервал .памяти цйфроврто нерекурбйвного фильтра возрос в два рааз и стал равен 2.N, где N - это число регистров памяти 1-i блока задержки Т. Рассуждая аналогично, получим, что 50 при некотором произвольном значении Nrp- . интервал памяти .описываемого цифрового нерекурсивного фильтра будет равен:
.N, (16) где L- интервал памяти цифрового нерекурсивного фильтра; ..
N-количество регистров памяти;
Nrp - число группируемых отсчетов.
Таким образом.осуществлял предварительное группирование Nrp отсчетов в соответствии с формулой (11) и лишь затем
35
55
осуществляя процесс цифровой фильтрации в соответствии с формулой (9) удается получить структуру цимфрового нерекурсивного фильтра, обладающего возможностью изменения протяженности его весовой функции и, следовательно, интервала памяти в широких пределах не прибегая к дополнительным аппаратурным (и энергетическим) затратам, причем благодаря использованию управляемых весовых блоков 2-j (умножителей) при операции цифровой фильтраций можно дискретно изменять (выбирать) форму весовой функции, (вход Ф на фиг, 1 - показывает номер сглаживающей функции). В результате предварительного группирования отсчётовГ входного сигнала, .ча стЬта-следования обсчетов с выхода первого сумматора 3 по ртноШёнию к частоте следования входных отсчетов уменьшилась в Nlrp раз поэтому дл я восстановления ис- . ходной частоты следования отсчетов-на выг ходе цифрового рекурсивного фильтра, необходимо провести процесс интерполяции. В описываемом цифровом нерекурсивном фил ьтре тгроЦ есс интерполяции-. ocyaiectB jieTCflrd помощью второго делите-, ля. 12, вычислительных блоков 13-16, регистров пймяти 7-8 и третьего сумматора 17. Квад ратачйая интерполяция осуществляется по четырём узловым точкам y(i) ;(фиг.4), причем первая, вторая и третья узлЪвые точки служат для расчета первого полинома, а вторая третья и четвёртая точки служат для расчета второго полинома. После расчета г1олйном6в в указанйьгх узловых точках расчитывается их среднее арифметическое по формуле.; -i ;:i:/;- -t: :;V : -; :-- v-:: : :-: --:
l3(F51+P2)/2,
(17).
причем полином Р используется для расчета промежуточных значений между второй и третьей узловыми точками. Такая процедура позволяет повысить точность интерполяции; по сравнению :с квадратической интерполяцией по трём узловым точкам, .: .. В общем виде для случая квадратичной интерполяции по первым трем точкам (см. Бронштейн И.Н., Семендяев К.А., Справочник по математике, М.: Наука, 1981, с.663) имеем: , .:- -.-.-,--. . ,- .: . - ., ....
-::: (х-х2)(х-хз): ; .
У (xl -х2)(х1 -хЗ) +-. у2(х-х1 )(х-хЗ) , -.- ( х2 - xl ) ( х2 - хЗ )
уЗ(х-х1)(х-х2) рсЗ -х1 )(хЗ -х2 )
.08)
Принимая , и (0), (j) получим, что
, ,
(Nrp), (2Nrp). Тогда
Принимая Vi -гт- -1, получим p.Sfplv.f vr-lb 1
)- о .:,1
(ii-0-.Цг- . ;
Принимая Vi -гт- -1, получим p.Sfplv.f vr-lb 1
.:,1






| название | год | авторы | номер документа |
|---|---|---|---|
| Адаптивный цифровой фильтр | 1987 |
|
SU1494212A1 |
| Специализированный процессор для цифровой фильтрации | 1989 |
|
SU1631558A1 |
| Устройство для вычисления коэффициентов нерекурсивных полосовых фильтров | 1988 |
|
SU1647587A1 |
| Цифровой перестраиваемый полосовой фильтр | 1982 |
|
SU1166274A1 |
| Нерекурсивный цифровой фильтрдециматор | 1984 |
|
SU1195420A2 |
| Цифровой нерекурсивный фильтр | 1986 |
|
SU1350826A2 |
| Нерекурсивный цифровой фильтр-дециматор | 1986 |
|
SU1354394A1 |
| Устройство для цифровой фильтрации | 1987 |
|
SU1483606A2 |
| Цифровой интерполирующий фильтр | 1988 |
|
SU1653132A1 |
| Многочастотный цифровой фильтр | 1987 |
|
SU1474827A1 |
(21)
;; (мгрл)-jv(/-2Nrp),
.- . .л - . Т
:: ЗДГ--;... . .:
: + lMЈMizJ pJ
.Л:; :;:,Ч 2 Nrp / ...;..,.,:
Для полученного полинома P1(j), величина j изменяется в пределах от 0 до (2Nrp- 1) с шагом 1. Аналогично для второго полинома и второй, третьей и четвертой узловых точек имеем: : -
. (х-хЗ)(х-х4) Л , ;/.. ; У (х2 -хЗ)(х2 -х4) ;;:
л:. Г:у3 (х - х2) (х - х4;},: У
: .;:/ ( хЗ - х2 ) (хЗ - х4 ). .;,--..;.. .
V ;у4(х -х2 )(х -хЗ) ,г ,.(х4 -х2)(х4 -хЗ)
(22)
Принимая , и (0). (j) получим, чтчто : .... .- .. . -.. ,.
. , . .. ;-:Vv.. (23) -:- ,: ,:.;Л v: - -W: (24) .. , v : . :. (25)
;; (Nrp). ::: Г::: :.-. (26) (2Nrp) .. j ;: ;..; (27) Тогда . ,., ., ;.- : : .- -; :V;; :: . .:..:: ;
P20
.S(NrpKj-2Nrp)(j-3Nrp)
. S(2Nrp)()(j-3 Nrp)
:r-.V.
+
rp
, S(3Nrp)(j-Nrp(j-2Nrp:)
(28)
Для полученного полинома P2(j) величина j изменяется в пределах от Nrp до 3Nrp-1; тогда в соответствии с формулой (18) получим:. : .
. гШ+ШЬ
(
x( Vi -5 ) V, ( Vi - 1 ) . (30)
Так как для полученного полинома величина j изменяется в предела от Nrp до 2Nrp, а величина Vi изменяется в пределах от 0 до
. . .. -.Л .. .. . .
1 с шагом тп- . Причем с выходов четверто0
5
0
5
0
5
0
5
k I
- , -NrP ... ...... , .. . ......... .,
ro 9, третьего 8 и второго 7 регистров памяти снимаются узловые отсчёты S(0), S(IMrp) и S(2Nrp) соответственно; а с выхода первого суммато ра 3 снимается узловой отсчет S(3Nrp), которые подаются на пе рвые вхоД1н четвертого 16, третьего 15, второго 14 и первого .1.3. вычислительных блоков соответственно. Функциональное назначение вычислительны блоков 16-13 состоит в вычислении первого, втбрбгб , tpetber o H четвертого слагаемых .собт ветств ённо с формулой (30), причем переменная Vr, используется в каждом слагаемом формулы (30) и рассчитыва.ется во втором делителе 12, а затем подаётся на вторые входы каждого вычислительного блока 13-1.6. Текущее значение/переменной Vi рассчитывается во втором делителе 12 в соответствии с формулой (4), причем на первый вход второго делителя 12 подается текущее значение кода изменяющего своё состояние от 0 до Nrp-1, а на второй вход второго делителя 12 подается значение Nrp с управляющего входа
ЦИФРОВОГО НерекурСИВНОГО фИЛЬТра. В COOT;
ветствии с формулой (30) текущие значения, первого, второго , третьего и четвертого слагаемых рассчитывается вычислительными блоками 16, 15, 14, 13 соответственно, а коды, записанные в вычислительные блоки 16г13 рассчитываются по формулам (8), (7), (6), (5) соответственно. . . -..,: С выхода третьего сумматора снимается текущее значение полинома, рассчй- танного по формуле (30) и подается на вьгход цифрового интерполяционного фильтра. .. Изобретение может быть применено в устройствах цифровой обработки сигналов, при адаптивной цифровой фильтрации.
Использование предложенной совокупности блоков и связей по сравнению с прототипом существенно . расширяет
функциональные возможности, а именно осуществление операции группирования в цифровом нерекурсивном фильтре, обеспечивает расширение интервала памяти цифрового, нерекурсивного фильтра .и его весовой функции без увеличения количества его звеньев, изменение величины группирования отсчетов Nrp позволяет электронным путем в широких пределах перестраивать интервал памяти цифрового нерекурсивного фильтра без дополнительных аппаратурных и энергетических затрат. Изменение в широких пределах и нтервалгг памяти и весовой функции фильтра эквивалентно регулировке амплитудно-частотной характеристики фильтра, - ; :: ; ; - :, Ф о р м у л а и so б р ё т и я Г Цифровой нерекурсивный фильтр, содержащий первый регистр памяти, последовательно соединенные блок задержки, блок умножителей, второй вход кбторого является входом задания коэффициента умножения и первый- сумматор, а также последовательно соединенные второй, тре- тий и четвертый регистры памяти, о т. л и ч а- ю.щ и и с я тем, что, с целью упрощения -регулировки амплитудно-частотной характеристики, введены второй сумматор, первый вход которого является информационным входом цифрового нерекурсивного фильт- ра, выход соединен с информационным
входом первого регистра памяти, первый делитель первый вход которого соединен с выходом первого регистра памяти и вторым входом второго сумматора, а выход соединен с информационным входом блока задержки, последовательно соединенные счетчик импульсов, информационный вход которого соединен с входом синхронизации первого регистра памяти и является тактовым входом цифрового нерекурсивного фильтра, и блок сравнения, выход которого соединен с входом установки в О счетчика импульсов и первого регистра памяти и входами синхронизации блока задержки второго, третьего и четвертого регистров памяти, второй делитель, первый вход которого соединен с выходом счетчика импульсов, второй вход соединён с вторыми- входами первого делителя и. блока сравнения и является входом коэффициента деления, третий сумматор, выход которого является выходом цифрового нерекурсивного фильтра, а также первый, второй третий и четвертый .вычислительные блоки, первые входы кото-, рых соединены с выходом второго делителя, вторые входы соединены.соответственно с выходом первого сумматора, второго регистра памяти, третьего регистра памяти и четвертого регистра памяти, а выходы соединены с соответствующими входами третьего сумматора:; -;..-.-. ..-... Фнг. 1
Фиг. 3
(i)
Фиг. 4
Авторы
Даты
1993-01-07—Публикация
1990-01-11—Подача