Учебное пособие по математике Советский патент 1993 года по МПК G09B23/02 

Изобретение относится к демонстрационным приборам, в частности к средствам обучения, и может быть использовано при изучении математики в высших учебных заведениях.

Известно учебное пособие по математике, выбранное в качестве прототипа, содержащее коробку с прозрачным планшетом, окантованным намагниченным материалом, на котором нанесена прямоугольная система координат,, источник света, набор прозрачных пластин, каждая из которых имеет намагниченную кромку, стержень, шарнир- но закрепленный на планшете в начале координат, и планку, свободно установленную на стержне перпендикулярно ему. Пособие позволяет иллюстрировать метод градиента решения задач линейного программирования.

Недостатком известной конструкции является отсутствие зримой модели целевой функции, что значительно сужает дидактические возможности пособия. Обучаемые не могут наблюдать проекционнуюсвязьобласти допустимых решений с соответствующей зоной на целевой функции, не могут видеть возрастание (убывание) целевой функции и точку ее экстремума. В силу этого, учебное пособие не позволяет иллюстрировать многие ключевые положения теории линейного программирования.

Целью изобретения является расширение дидактических возможностей пособия и улучшение наглядности обучения путем обеспечения возможности демонстрации понятия целевой функции.:

Указанная цель достигается при помощи прозрачной пластины для моделирования целевых функций, а также при помощи прямых, усеченных призм, имитирующих проекционную связь определенной области допу- стимых решений с соответствующей зоной на целевой функции, Сопоставительный анализ с прототипом позволяет сделать вывод, что заявляемое учебное пособие отличается тем, что оно имеет средство моделирования линейных функций двух переменных в виде прозрачной пластины для

сл

гагяД

представления целевой функции, имеющей стрелочный указатель направления возрастания или убывания целевой функции и ползунок - имитатор линии равного значения, и набор модифицированных по форме прямых, усеченных призм для имитации проекционной связи области допустимых решений с соответствующей зоной на целевой функции, предназначенных для установки на планшете, закрепляемых на основании и на пластинах, имеющих намагниченную кромку, при этом прозрачная пластина для представления целевой функции установлена на планшете посредством оси расположенной в начале координат, а осно вания призм имеют намагниченный участок для закрепления на пластинах.

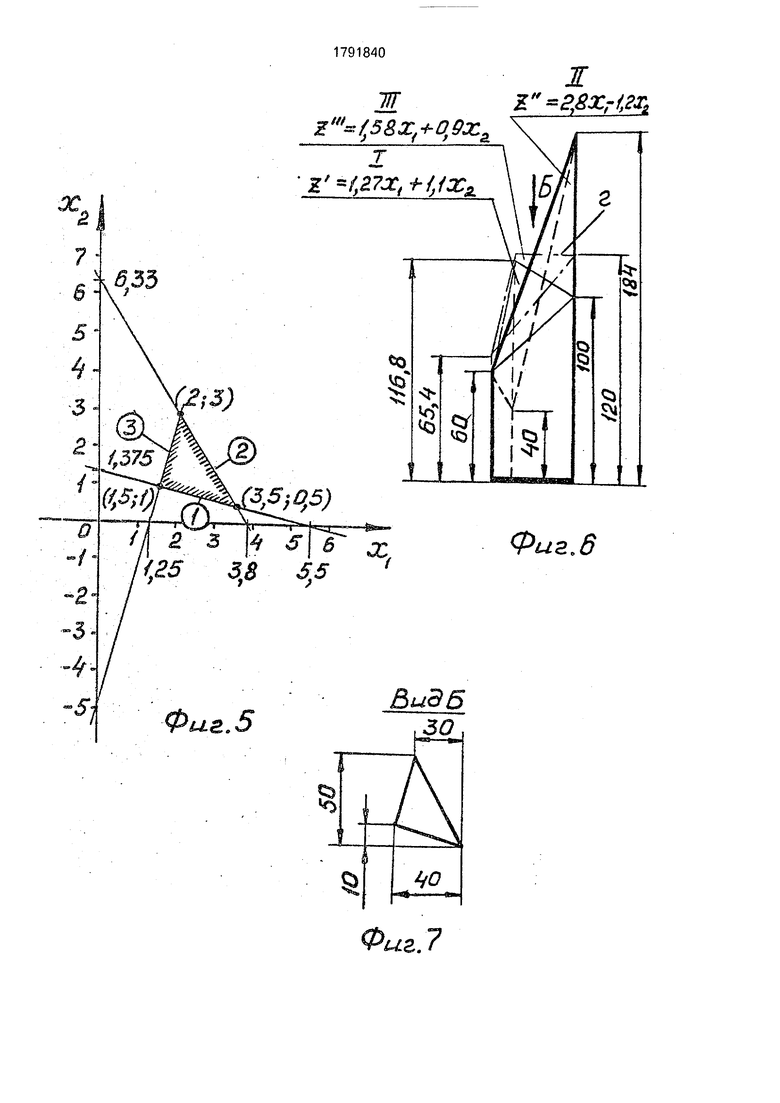
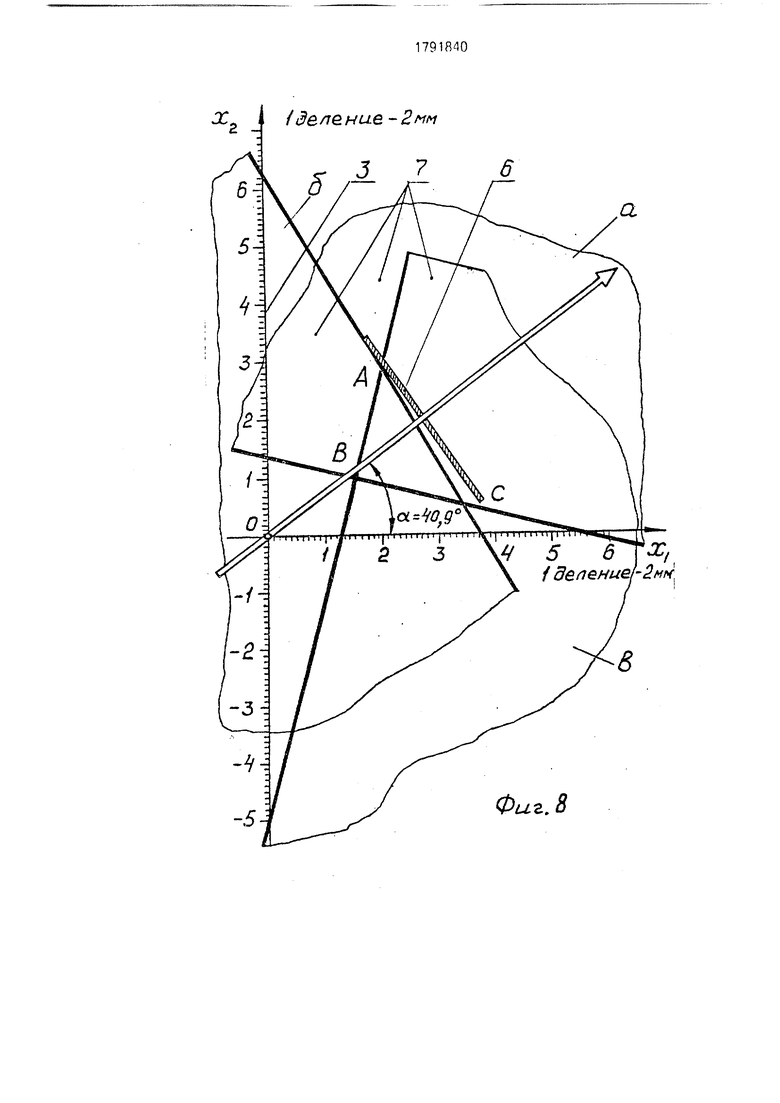
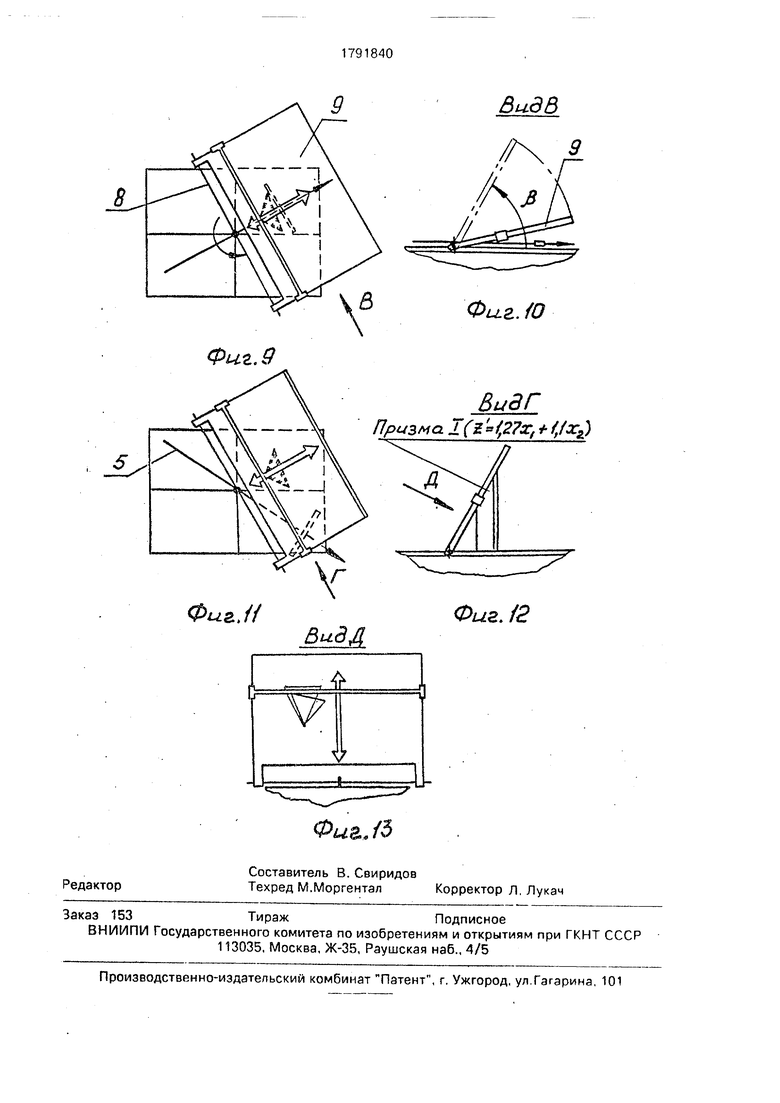
На фиг.1 показано пособие, вид спереди; на фиг.2 - то же, вид слева: на фиг.З - то же, вид сверху; на фиг.4 - разрез А-А на фиг.2; ка фиг.5- проектный расчеттреуголь- .ной призмы; на фиг.6 - набор из трех треугольных призм; на фиг.7 - вид по стрелке Б на фиг.6; на фиг.8 - взаимодействие элементов пособия при определении совокупности неотрицательных переменных xi и ха в конкретной задаче линейного программирования; на фиг.9 - поворот пластины до совмещения стрелочного указателя с направлением стержня; на фиг.10 - поворот пластины вокруг оси на угол фиг,11 - положение стержня вне области допустимых решений; на фиг.12 - установка треугольной призмы на планшете; на фиг.13- фиксация точки максимума целевой функции.

Устройство содержит коробку 1 с прозрачным планшетом 2, на котором нанесена прямоугольная система координат 3, источник света 4, шарнирно закрепленный на планшете в начале координат стержень 5, планку 6, свободно установленную на стер- жне перпендикулярно ему. и набор пластин 7. Прозрачный планшет 2 имеет намагниченную окантовку (на фиг.З окантовка показана жирными линиями), каждая из прозрачных пластин 7 имеет намагниченную кромку (на фиг.8 намагниченные кромки показаны жирными линиями). Намагниченная окантовка и намагниченные кромки предназначены для фиксации прозрачных пластин 7 на прозрачном планшете 2.

Кроме стержня 5, в начале координат шарнирно крепится ось 8, вокруг которой может поворачиваться прямоугольная прозрачная пластина 9, моделирующая целевые функции двух переменных. На пластине 9 нарисован стрелочный указатель (показывает возрастание или убывание целевой

-

функции), пересекающий начало координат и направленный по нормали к оси 8. На пластине 9 имеется ползунок 10 - имитатор линии равного значения линейной формы.

5 Пособие снабжено набором модифицированных по форме прямых, усеченных призм с основаниями, имеющими намагниченный участок. Намагниченные участки служат для закрепления призм на прозрачных пласти10 нах7.

Стержень 5 предназначен для показа направления градиента целевой функции, а планка 6 - для показа линий уровня целевой функции.

15 Моделируя целевые функции и располагая набором призм с необходимой модификацией формы, можно осуществлять наглядную геометрическую интерпретацию задач линейного программирования в

20 трехмерном пространстве, иллюстрируя в процессе обучения многие ключевые положения теории линейного программирования. Круг дидактических задач при этом не ограничивается и может быть расширен

25 обучающим. Соответственно, пополняемым будет и набор модифицированных по форме прямых, усеченных призм,

Пусть, например, перед обучающим стоит дидактическая задача: показать, что ре30 шение задачи линейного программирования

Z cixi + C2X2 max

Э11Х1 + 312X2 2 Ь1 321X1 + 322X2 S b2

35 аз 1x1 + аз2Х2 Ьз

находится в одной из вершин многоугольника допустимых решений. Требуется показать также, что линейная форма одного вида достигает максимума в какой-то одной вер40 шине области допустимых решений, а линейная форма другого вида - в другой вершине. Обучаемым необходимо, кроме того, продемонстрировать существование множества решений.

45Эти сложные для умозрительного понимания вопросы можно рассмотреть, имея в наборе модифицированных по форме призм три треугольные призмы чьи основания идентичны одной и той же области допусти50 мых решений, а наклоны верхних граней различны и соответствуют неодинаковому наклону к началу координат трех неодинаковых целевых функций.

Размеры, необходимые для изготовле55 ния призм, можно определить, выполнив проектный расчет, который заключается в следующем.

Вначале задаются целесообразной совокупностью неотрицательных переменных

xi и Х2 а вершинах треугольника допустимых решений (фиг.5). Затем формируют ограничения, используя уравнения:

К -Х21

хт-х1 Xj2 x12-Kxi1;

х,.-4

где X i, Х 2 отрезки, отсекаемые на координатных осях прямыми, представляющими собой ограничения;

х11, х12 и х21, Х22 - координаты вершин треугольника допустимых решений, причем вершин, принадлежащих одной и той же стороне треугольника допустимых решений;

j - номер стороны треугольника допустимых решений, j 1, 2, 3 (фиг.5).

Определяют коэффициенты при переменных и свободные члены ограничений

ам Х 2;а|2-Х 1;Ь (2)

i 1.2, 3.

Задаются целесообразными длинами Z и Z каких-либо двух боковых ребер каждой из призм, Длины боковых ребер призмы в принятом масштабе равны значениям целевой функции в вершинах треугольника решений.

Решая систему уравнений

Z C1X1 + С2Х2, (3)

Z С1Х1 + С2Х2,

находят коэффициенты ci и С2 при переменных целевой функции.

Здесь xi и Х2 - координаты вершин треугольника допустимых решений.

Подсчитывают длину третьего ребра;

Z С1Х1 + С2Х2,(4)

Полученные в результате проектного расчета призм размеры даны на фиг.б и 7.

В соответствии с фиг.б, 6 и уравнениями 1-4 имеем систему ограничений . - 1,375x1-5,5x2 -7,56;

6,33x1 +3,8x2 24;

-5xi + 1,25x2 -6,25, и три целевые функции

Zi 1,27xi + 1,1 Х2;

Z2 2,8xi-1.2x2;

2з 1,58x1 + 0,9 Х2.

Учебное пособие работает следующим образом.

Пластину 9 устанавливают вдоль оси Х2 в вертикальное положение. Пластину а располагают на планшете так, чтобы ее намагниченный край проходил через точки xi 5,5 и Х2 1,375. Пластину b устанавливают так, чтобы намагниченный ее край прошел через точки xi 3,8 и Х2 6,33, намагниченный

край пластины b проходит через точки xi 1,25 и Х2 - 5.

Намагниченные края пластин образуют треугольник ABC, представляющий собой 5 область допустимых решений, Так как этот треугольник (и только он) закрыт всеми тремя пластинами, то при подсвете лампой 4 он будет самым темным участком на планшете 2. Это позволяет отчетливо видеть область 10 допустимых решений и облегчает работу с ней при пользовании прибором.

Определяют градиент первой целевой функции

15. dZi т dZi т

grad Zi - i +-г-1 j; oxi dx2

(5)

gradZi 1,271-.- 1,1 j. Находят угол а, который направление 20 t градиента образует с направлением оси х;

tg О-

dZi dZi dX2 dxi

(6)

tga 1,1/1.27 -0,866, откуда а 40,9°.

Устанавливают стержень 5 под углом а. 40,9° к оси XL а планку б перемещают по стержню 5 до крайней вершины области допустимых решений, т.е. до точки А. Координаты этой точки (xi 2, Х2 3) должны являться решением поставленной задачи.

Находят угол / между направлением градиента и направлением возрастания собственно целевой функции;

0

tg/3

Zi

cIZi dxi

dZi

dX2/

dZiV

dxij

+

dZi)2 dx2J

(7)

tg /S 2,8/( Y 1,272 + 1,12) 1,68, откуда /5 59,2°.

45

В положении, близком к горизонтальному, поворачивают пластину 9 вокруг шарнира так, чтобы нарисованный на пластине 9 стрелочный указатель совпал с направлени- 0 ем стержня 5. Затем пластину 9 поворачивают вокруг оси 8 на угол / - угол наклона : целевой функции к началу координат, В ; этом положении прозрачная пластина Q представляет линейную целевую функцию 5 Zi 1,27xi + 1,1 Х2.

Поворачивая стержень 5, устанавливают его так, чтобы он не пересекал область допустимых решений. На планшет 2 устанавливают призму, соответствующую целевой функции Zi 1,27 xi + 1,1 Х2. Основание

призмы должно совпадать с самым темным участком (треугольником допустимых решений), В этом положении призму закрепляют на основании, имеющем намагниченный участок, и на пластинах, имеющих намагни- ценную кромку.

Если углы а и ft подсчитаны правильно, верхняя наклонная грань призмы соприкоснется с плоскостью пластины 9. Наблюдают проекционную связь области допустимых решений с соответствующей зоной на целевой функции. Перемещая ползунок 10 до наиболее удаленной вершины наклонной грани призмы, фиксируют точку максимума целевой функции. Убеждаются, что точка максимума проецируется именно в вершину многоугольника (в данном случае, треугольника) допустимых решений.

Используя формулы (5, 6 и 7), выполняют аналогичные действия, располагая вначале на области допустимых решений призму, соответствующую 7.2 2,8 xi -1,2 Х2, а затем призму, соответствующую Zo 1,58x1 + 0,9x2.

В первом случае, перемещая ползунок 10, .убеждаются, что -различные линейные формы достигают максимума в разных вершинах одной и той же области допустимых решений. Во втором случае наблюдают бесчисленное множество решений - ползунок 10 совпадает с одной из ciopohf(стороной г треугольника, представляюа,его собой наклонную грань призмы (фиг.6 и 13). Все точки, принадлежащие стороне г являются точками максимума целевой функции.

Положительный эффект заявляемого учебного пособия; зримая модель целевой функции в сочетании с различными по форме усеченными призмами позволяет изучать теорию линейного программирования в различных дидактических аспектах, улучшая одновременно наглядность обуиения.

Формула изобретения Учебное пособие по математике, содержащее коробку с прозрачным планшетом, окантованным намагниченным материалом, на котором нанесена прямоугольная система координат, источник света, набор прозрачных пластин, каждая из которых имеет намагниченную кромку, стержень, шарнир- но закрепленный на планшете в начале координат, и планку, свободно установленную на стержне перпендикулярно ему, отличающееся тем, что, с целью расширения дидактических возможностей и улучшения наглядности обучения путем обеспечения возможности демонстрации понятия целевой функции, оно имеет средство моделирования линейных функций двух переменных в виде прозрачной пластины для представления целевой функции, имеющей стрелочный указатель направления возрастания или убывания целевой функции и ползунок- имитатор линии равного значения, и набор модифицированных по форме прямых, усеченных призм для имитации проекционной связи области допустимых решений с соответствующей зоной на целевой функции, предназначенных для установки на планшете, закрепляемых на основании и на пластинах, имеющих намагниченную кромку, при этом прозрачная пластина для представления целевой функции установлена на планшете посредством оси, расположенной в начале координат, а основания призм имеют, намагниченный участок для закрепления на пластинах.

Фиг. 9

Изобретение относится к демонстрационным приборам и может быть использовано при изучении теории линейного программирования и позволяет расширить дидактические возможности известного, улучшить наглядности обучения. Сущность 2 изобретения состоит п наличии дополнительного средства моделирования линейных функций двух переменных в виде прозрачной пластины для представления целевой функции, имеющей стрелочный указатель направления возрастания или убывания целевой функции, и ползунок- имитатор линии равного значения, а также в наличии набора модифицированных по форме прямых, усеченных призм для имитации проекционной связи области допустимых решений с соответствующей зоной на целевой функции.13 ил.

Фи&М

ВиВЛ

Фиг. /2