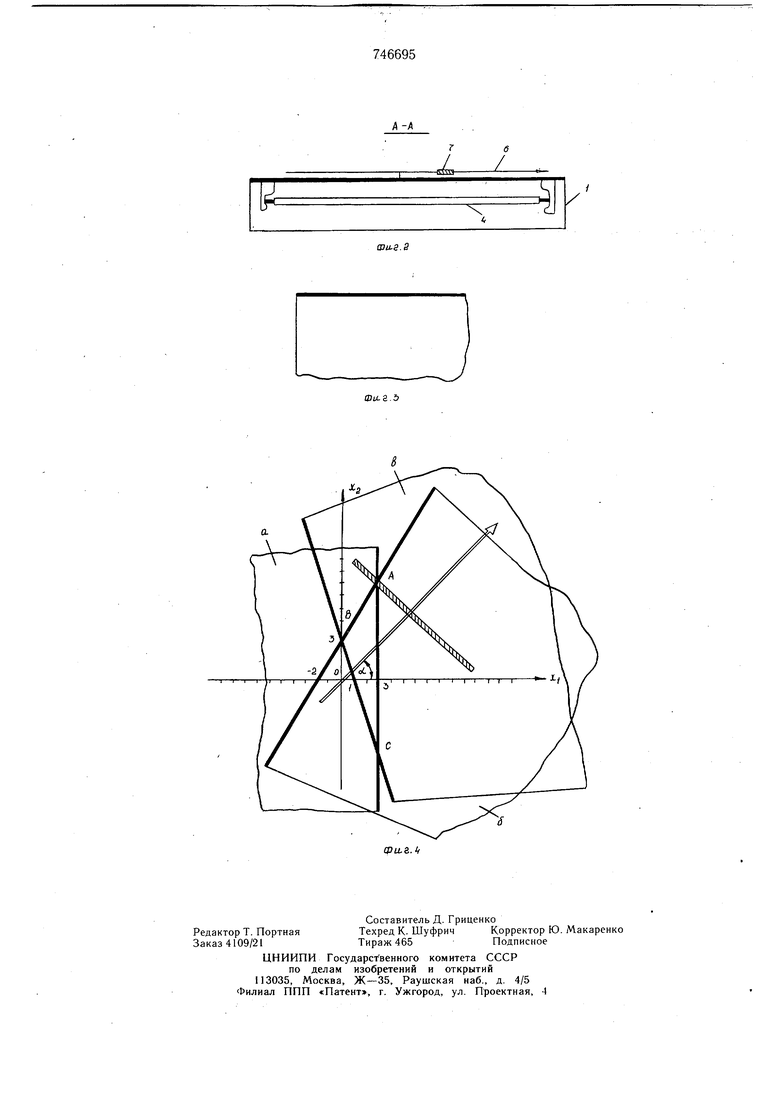
(54) УЧЕБНОЕ ПОСОБИЕ ПО МАТЕМАТИКЕ Изобретение относится к учебным пособиям по математике и может быть использовано в учебном процессе в высших учебных заведениях. Известно учебное пособие по математике, содержащее коробку с прозрачным планшетом, на котором нанесена прямоугольная система координат, источник света, набор прозрачных пластин, позволяет иллюстрировать решение системы двух линейных уравнений 1. Однако оно не дает возможности иллюстрировать метод градиента решения задач линейного программирования. Цель изобретения - расширение диапазона решаемых задач путем обеспечения наглядной иллюстрации метода градиента решения задач линейного программирования. Для достижения этой цели пособие снабжено стержнем, шарнирно закрепленньтм на планшете в начале координат, и планкой, свободно установленной на стержне перпендикулярно ему, а прозрачный планшет и одна сторона каждой из прозрачных пластин окантована намагниченным материалом. На фиг. .1 представлен-, пособие, общий вид; на фиг. 2 - разрез А-А на фиг. 1; на фиг. 3 - прозрачная пластина; на фиг. 4 пример работы пособия. Учебное пособие по математике содержит коробку 1 с прозрачньш планшетом 2, на котором нанесена прямоугольная система координат 3, источник света 4, шарнирно закрепленный на планшете в начале координат стержень 5, планку 6, свободно установленную на стержне перпендикулярно ему, и набор пластин 7. Прозрачный планшет 2 и одна из сторон каждой из прозрачных пластин 7 окантованы намагниченным материалом (на фиг. 1 и 3 окантовки показаны жирными линиями). Намагниченные окантовки предназначены для фиксации прозрачных пластин 7 на прозрачном планшете 2. Учебное пособие позволяет наглядно иллюстрировать метод градиента решения следующей задачи линейного программирования. Найти совокупность неотрицательных переменных Xi и хг, удовлетворяющих систему ограничений aiiXi + в 02 I X, + вг , + апгхг вщ при которых целевая функция Z + + СгХг достигает экстремума (максимума или минимума). Каждая пластина 7 предназначена для закрывания на планшете 2 множества решений одного из неравенств системы ограничений, т.е. используется m пластин. Стержень 5 предназначен для показа направления градиента целевой функции, а планка 6 для показа линий уровня целевой функции. Ярижер.ОпреДеЛяют совокупТйость неотрицательных переменных х и xj, удовлетворяющих системе ограничений л:, 3 -Зх, + 2.х:г 6 У V -Зл;, -Х2 -3 j при которых линейная целевая функция Z 2xi + 2x2 достигает максимума. Пластину а располагают на планшете параллельно оси ху, так, чтобы ее намагниченный край проходил через точку х 3. Пластину б устанавливают так,, чтобы намагниченный ее край проходил через точки Xi -2 и Xz 3, намагниченный край пластины 8 проходит через точки Xi ц xz 3. Намагниченные края пластин образуют треугольник ABC, представляющий собой область допустимых решений. Так как этот треугольник (и только он) закрыт всеми тремя пластинами, то при подсвете лампой 4 он будет самым темным участком на пл,аншете 2. Определяют градиент целевой функции ff;- + -3V 2 + J Находят угол а, который образует направление градиента с направлением igd -|- t , откуда d 45°. d KI Устанавливают стержень 5 под углом d 45° к оси Х{, а планку 6 перемешают п) стержню 5 до крайней вершины области допустимых решений, т.е. до точки А. Координаты этой точки (х 3, xz 7,5) являются решением поставленной задачи. Формула изобретения Учебное пособие по математике, содержащее, коробку с прозрачным планшетом, на котором нанесена прямоугольная система координат, источник света и набор прозрачных пластин, отличающееся тем, что, с целью расширения диапазона решаемых задач путем обеспечения наглядной иллюстрации метода градиента решения задач линейного программирования, оно снабжено стержнем, шарнирно закрепленным на планшете в начале координат, и планкой, свободно установленной на стержне перпендикулярно ему, а прозрачный планшет и одна сторона каждой из прозрачных пластин окантованы намагниченным материалом. Источники информации, принятые во внимание при экспертизе 1. Авторское свидетельство СССР № 2000915, кл. G 09 б 23/02, 1967.
- А

| название | год | авторы | номер документа |
|---|---|---|---|
| Учебное пособие по математике | 1990 |
|
SU1791840A1 |
| Наглядное пособие по математике | 1990 |
|
SU1805489A1 |
| НАГЛЯДНОЕ ПОСОБИЕ ПО МАТЕМАТИКЕ | 2000 |
|
RU2166212C1 |
| Устройство для обучения основам оптимизации | 1980 |
|
SU875441A1 |
| Учебное наглядное пособие по математике | 1950 |
|
SU88175A1 |
| Учебное наглядное пособие по математике | 1949 |
|
SU88988A1 |
| УЧЕБНЫЙ ПРИБОР ПО МАТЕМАТИКЕ | 1998 |
|
RU2127451C1 |
| Учебное пособие по математике | 1980 |
|
SU1061172A1 |
| Учебный прибор по математике | 1986 |
|
SU1370661A1 |
| Демонстрационный прибор по математике | 1982 |
|
SU1075291A1 |



Авторы
Даты
1980-07-05—Публикация
1978-06-15—Подача