Настоящее изобретение относится к способам наведения летательных аппаратов на радиоизлучающие воздушные объекты, в частности к способам наведения летательных аппаратов при использовании угломерных двухпозиционных радиолокационных систем.
В авиации обширный класс воздушных объектов составляют объекты, на которых размещаются источники радиоизлучений. Наблюдение за такими радиоизлучающими объектами (РИО) может осуществляться на основе приема сигналов, излучаемых их радиоэлектронными средствами, с помощью угломерных двухпозиционных радиолокационных систем [Белик Б.В., Белов С.Г., Верба B.C. и др. Авиационные системы радиоуправления / Под ред. B.C. Вербы, В.И. Меркулова. - М.: «Радиотехника», 2014, стр. 187-212].
Эффективность применения угломерных двухпозиционных систем (УДПРЛС) во многом зависит от способа управления летательными аппаратами (ЛА), на которых размещаются приемные позиции (ПП) этой системы. Обусловлено это тем, что в процессе управления изменяется взаимное пространственное положение ЛА и РИО, в значительной степени влияющее на условия наблюдения и точность определения местоположения радиоизлучающих объектов [Дрогалин В.В., Ефимов В.А., Меркулов В.И. и др. Способы оценивания точности определения местоположения источников радиоизлучения пассивной угломерной двухпозиционной бортовой радиолокационной системой // Успехи современной радиоэлектроники. Зарубежная радиоэлектроника, 2003, №5, стр. 22-38].
При применении УДПРЛС, как правило, необходимо одновременно решать две задачи, а именно: задачу наведения ЛА на РИО и задачу траекторного управления ЛА для создания наиболее благоприятных условий для высококачественного радиолокационного наблюдения за РИО. В связи с этим разрабатываются способы, предусматривающие решение задачи управления процессом наблюдения с одновременным наведением на РИО. При этом наиболее сложной является организация управления ЛА при наличии опасных зон для полетов. К опасным зонам для полетов, в частности, относятся зоны интенсивного самолетовождения, районы с опасной метеообстановкой (грозы, смерчи, тайфуны), участки с действующими вулканами, запретные зоны для полетов ЛА.
Известно несколько способов наведения двух самолетов по курсу в горизонтальной плоскости [Патент РФ №2256870, 20.07.2005. Бюл. №20; Патент РФ №2262649, 20.10.2005. Бюл. №29; Патент РФ №2308093, 10.10.2007. Бюл. №28], согласно которым наводящийся на РИО самолет, называемый в дальнейшем для краткости первым ЛА, управляется в соответствии с одним из существующих способов самонаведения, а второй самолет - второй ЛА выводится на прямую, ортогональную линии визирования первый ЛА-РИО и проходящую через РИО, на которой существуют наилучшие условия для радиолокационного наблюдения за РИО.
Недостатками данных способов наведения являются большая продолжительность выхода второго ЛА на ортогональную линию визирования первый ЛА-РИО и невозможность обеспечения обхода опасных зон. В результате не гарантируется безопасность полета второго ЛА.
Наиболее близким аналогом (прототипом) к заявленному является градиентный способ управления ЛА по курсу в УДПРЛС, в котором управление вторым ЛА организуется таким образом, чтобы ошибка определения местоположения РИО в любой момент времени была минимально возможной [Меркулов В.И., Чернов B.C. Анализ методов наведения двухпозиционными пассивными системами воздушного базирования на источники радиоизлучения // Успехи современной радиоэлектроники, 2013, №7, стр. 35-37]. При реализации этого способа используются алгоритмы траекторного управления, полученные на основе теории принятия решений в одношаговых задачах оптимального управления с использованием градиентных методов нелинейного программирования. Данный способ не обеспечивает непосредственного решения задачи обхода опасных зон, но на его основе может быть разработан модифицированный способ проекции градиента, устраняющий указанный недостаток, имеющий место в процессе наведения второго ЛА при градиентном способе.
Отмеченный недостаток приводит к снижению эффективности применения УДПРЛС. Поэтому задачей настоящего изобретения является разработка способа управления ЛА по курсу в угломерной двухпозиционной радиолокационной системе, обеспечивающего самонаведение первого ЛА на РИО и создание вторым ЛА благоприятных условий для проведения радиолокационных наблюдений за РИО, в максимальной степени свободного от недостатка прототипа.
Поставленная задача достигается тем, что используют способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе, заключающийся в том, что измеряют значения пеленгов РИО на двух ЛА, прямоугольные координаты местоположения ЛА и их курсы, между летательными аппаратами осуществляют взаимный обмен результатами измерений пеленгов РИО, прямоугольных координат и курсов ЛА, оценивают прямоугольные координаты РИО и расстояния до РИО от летательных аппаратов, выбирают первый ЛА, осуществляют самонаведение первого ЛА на РИО, формируют параметр управления Δ2г вторым ЛА в соответствии с градиентным способом, в котором согласно изобретению дополнительно находят расстояние до опасной зоны ΔД, на основе полученной оценки расстояния определяют принадлежность текущего местоположения второго ЛА к опасной или безопасной зонам полетов, находят проекцию градиента ошибки местоопределения РИО на границу опасной зоны, рассчитывают требуемый курс ψ2пг полета второго ЛА вдоль границы опасной зоны, формируют параметр управления Δ2мпг вторым ЛА для полета вдоль границы опасной зоны в соответствии с модифицированным способом проекции градиента по соотношению:

где ψ2 - курс второго ЛА;
 - производная ΔД по времени;
- производная ΔД по времени;
κ пг - весовой коэффициент по курсу;
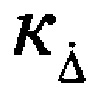 - весовой коэффициент;
- весовой коэффициент;
κ м - весовой коэффициент по ΔД и скорости его изменения,
и отклоняют органы управления второго ЛА по курсу с использованием параметра управления Δ2г для градиентного способа при нахождении второго ЛА в безопасной зоне и соответственно параметра управления Δ2мпг для модифицированного способа проекции градиента при нахождении ЛА на границе или внутри опасной зоны.
Благодаря введению, дополнительно по сравнению с прототипом, новой процедуры формирования параметра управления вторым ЛА успешно решается задача оптимизации условий радиолокационного наблюдения РИО при наличии опасных зон для полетов, что обеспечивает высокую точность наведения первого ЛА на РИО и существенное повышение живучести УДПРЛС в целом.
На фиг. 1 представлена упрощенная структурная схема возможного варианта УДПРЛС, реализующей предлагаемый способ управления.
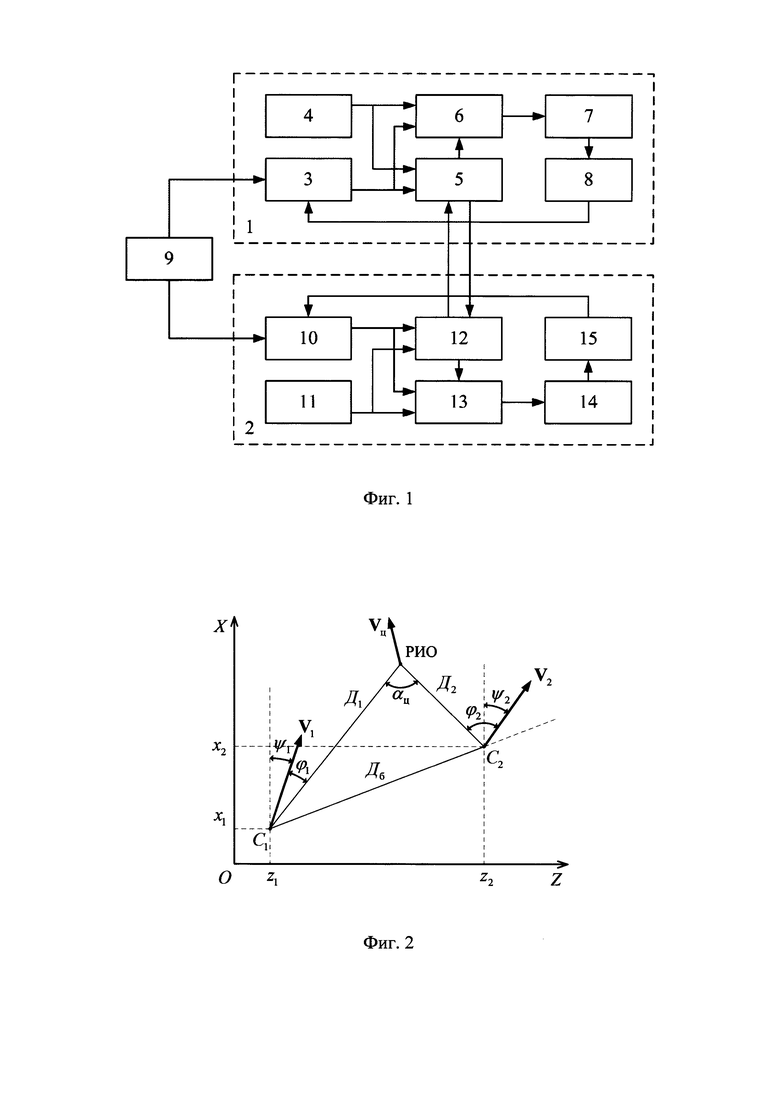
На фиг. 2 изображена геометрия взаимного расположения РИО и летательных аппаратов в горизонтальной плоскости.
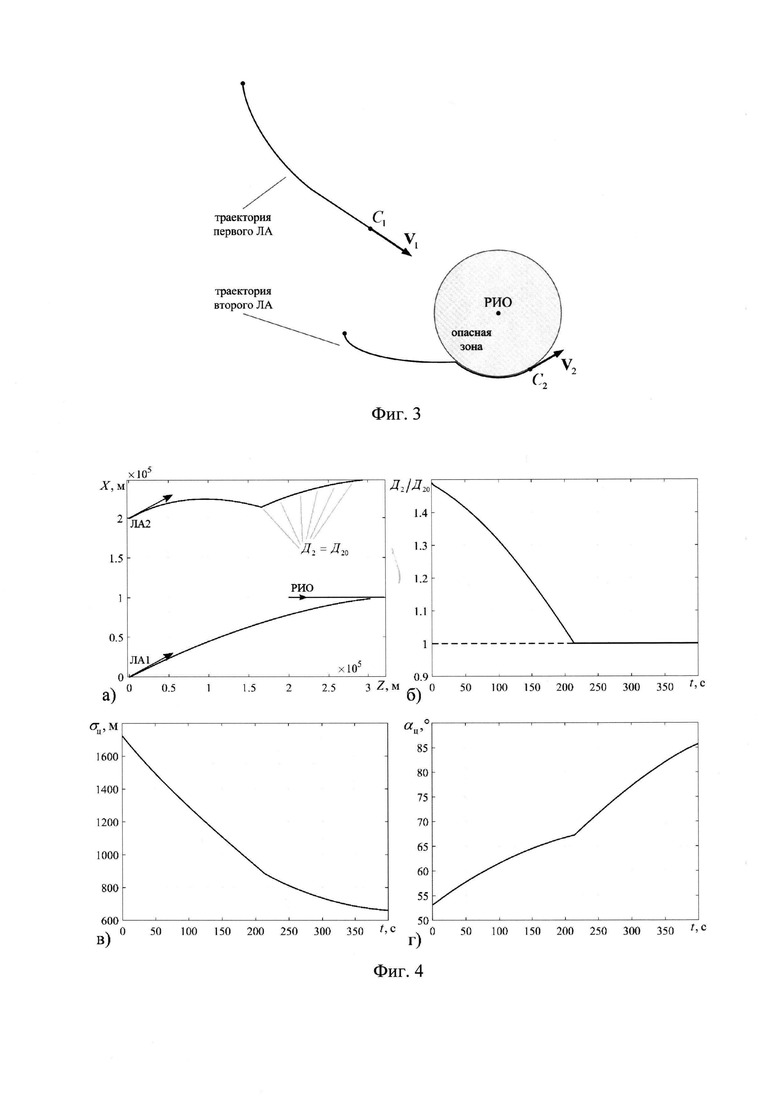
На фиг. 3 показаны типовые траектории движения ЛА при наличии опасной зоны для полетов.
На фиг. 4 приведены результаты моделирования процесса наведения двух ЛА и графики, иллюстрирующие характер изменения во времени важнейших показателей эффективности функционирования УДПРЛС.
Рассмотрим возможный вариант функционирования УДПРЛС при использовании заявленного способа управления летательными аппаратами по курсу.
В состав УДПРЛС (фиг. 1) входят первая и вторая ПП 1 и 2. ПП являются подвижными и размещаются соответственно на первом (8) и втором ЛА (15). Каждая ПП содержит одинаковый состав оборудования: угломер РЛС 3 (10), навигационную систему 4 (11), аппаратуру передачи данных 5 (12), вычислительную систему 6 (13) и систему автоматического управления 7 (14).
На фиг. 2 первый ЛА обозначен точкой С1, а второй ЛА - точкой С2. Заявленный способ обеспечивает оценивание координат РИО zц, хц в неподвижной невращающейся прямоугольной системе координат ZOX и расстояний до РИО от ЛА Д1 и Д2 (фиг. 2). Вектор первичных наблюдаемых параметров включает углы пеленгов РИО ϕ1 и ϕ2 в точках пеленгации, совпадающих с местами нахождения ЛА С1 и С2, а также прямоугольные координаты z1, х1 и z2, х2 и курсы ψ1, ψ2 летательных аппаратов С1 и С2.
Источник радиоизлучения, пространственно совпадающий с РИО 9 (фиг. 1), формирует радиосигналы, принимаемые в первой и второй ПП 1 и 2. Источником радиоизлучения могут быть различные радиоэлектронные системы, установленные на РИО. Угломеры 3 и 10, называемые также пеленгаторами, измеряют пеленги РИО ϕ1 и ϕ2 в каждой ПП. Навигационные системы 4 и 11 определяют местоположение летательных аппаратов z1, х1 и z2, х2 в прямоугольной системе координат и курсы ψ1, ψ2. Измеренные значения пеленгов РИО, прямоугольных координат и курсов ЛА с помощью аппаратуры передачи данных 5 и 12 передаются с одной позиции на другую. В вычислительные системы 6 и 13 поступают результаты измерения пеленгов РИО в двух позициях, прямоугольных координат и курсов ЛА. В вычислительных системах осуществляется формирование оценок прямоугольных координат РИО zц, хц и расстояний от ЛА до РИО Д1 и Д2, процедура получения которых подробно рассмотрена в [Дрогалин В.В., Ефимов В.А., Меркулов В.И. и др. Алгоритмы оценивания координат и параметров радиоизлучающих целей в угломерных двухпозиционных бортовых радиолокационных системах // Информационно-измерительные и управляющие системы, 2003, т. 1, №1, стр. 4-22] и [Верба B.C., Меркулов В.И., Дрогалин В.В. и др. Оценивание дальности и скорости в радиолокационных системах. Ч. 3 / Под ред. B.C. Вербы, В.И. Меркулова. - М.: «Радиотехника», 2010, стр. 382-396].
На основе заложенных в вычислительные системы критериев назначения летательных аппаратов выбирается первый ЛА для перехвата РИО, например ближайший к РИО, и второй ЛА, который обеспечивает наилучшие условия радиолокационных наблюдений РИО. В вычислительных системах вырабатываются параметры управления летательными аппаратами в зависимости от задач, возлагаемых на каждый ЛА.
Управление первым ЛА С1 при наведении на РИО может выполняться на основе любого из известных способов самонаведения, описанных в [Меркулов В.И., Чернов B.C., Гандурин В.А., Дрогалин В.В., Савельев А.Н. Авиационные системы радиоуправления: учебник для военных и гражданских ВУЗов и научно-исследовательских организаций / Под ред. В.И. Меркулова. - М.: Изд. ВВИА им. проф. Н.Е. Жуковского. 2008, стр. 85-94], например путем наведения в наивыгоднейшую упрежденную точку встречи либо способом прямого наведения.
Управление вторым ЛА направлено на минимизацию ошибок оценивания координат РИО и на обеспечение облета опасных зон. Алгоритмы траекторного управления вторым ЛА могут быть получены на основе следующих соображений.
Прежде всего следует учитывать, что траектория полета второго ЛА должна состоять из двух участков (фиг. 3). На первом участке, где отсутствует опасная зона для полетов, может применяться любой из известных способов траекторного управления наблюдением в УДПРЛС. Наиболее целесообразным является использование градиентного способа траекторного управления в силу таких его качеств, как максимально быстрое уменьшение ошибок местоопределения РИО в процессе наведения и наименьшее удаление летательных аппаратов друг от друга в пространстве. На втором участке второй ЛА должен обходить опасную зону, поэтому при разработке алгоритмов его траекторного управления необходимо учитывать соответствующие ограничения.
Оптимизация взаимного расположения ЛА и РИО на первом участке полета, осуществляемого на основе градиентного способа [Меркулов В.И., Чернов B.C. Анализ методов наведения двухпозиционными пассивными системами воздушного базирования на источники радиоизлучения // Успехи современной радиоэлектроники, 2013, №7, стр. 35-37], предусматривает организацию движения второго ЛА по специальной траектории. Параметры этой траектории определяются алгоритмом, полученным на основе градиентного способа поиска минимума целевой функции. Градиентом функции q(х), обозначаемым grad q(x) или ∇q(x), называется вектор, величина которого определяет скорость изменения функции q(х), а направление совпадает с направлением наибольшего возрастания этой функции. Вектор -∇q(x), указывающий направление наибольшего убывания функции q(х), называется антиградиентом функции q(х). Пусть n-мерный векторный аргумент х=(x1,…,xn) определяет состояние управляемого объекта (второго ЛА). Тогда градиент функции будет представлять вектор-столбец вида

Стратегия градиентного способа представляет собой последовательность шагов, каждый из которых содержит две операции:
1) определение направления наибольшей крутизны спуска, т.е. направления антиградиента функции q(х);
2) перемещение в выбранном направлении на заданное расстояние.
Математически стратегия градиентного способа получается, если перемещение Δxi на каждом шаге вдоль каждой из n осей будет пропорционально составляющей градиента ∂q(x)/∂xi в направлении этой оси.
В нашем случае градиент целевой функции является двухмерным (n=2).
В качестве целевой функции при траекторном управлении вторым ЛА в горизонтальной плоскости выбирается средняя квадратическая ошибка (СКО) местоопределения σц РИО, которая в случае одинаковых ошибок пеленгаторов σα1=σα2=σα приемных позиций С1 и С2 определяется следующим соотношением [Верба B.C., Меркулов В.И., Дрогалин В.В. и др. Оценивание дальности и скорости в радиолокационных системах. Ч. 3 / Под ред. B.C. Вербы, В.И. Меркулова. - М.: «Радиотехника», 2010, стр. 379-381]:

где αц - угол пересечения линий визирования из ПП на РИО (фиг. 2).
Для нахождения аналитического выражения требуемого курса необходимо взять частные производные 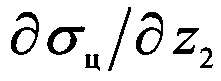 и
и 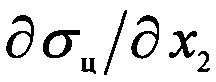 целевой функции σц по прямоугольным координатам z2 и х2.
целевой функции σц по прямоугольным координатам z2 и х2.
После вычисления частных производных требуемый курс ψ2г второго ЛА и параметр управления Δ2г им рассчитывают по формулам:

Однако выражение целевой функции σц (2) в явном виде не зависит от этих координат, поэтому его преобразуют к виду, удобному для нахождения градиента целевой функции. Необходимые для этого соответствующие уравнения связи определяются соотношениями [Меркулов В.И., Чернов B.C. Анализ методов наведения двухпозиционными пассивными системами воздушного базирования на источники радиоизлучения // Успехи современной радиоэлектроники, 2013, №7, стр. 36]:

где  - площадь треугольника С1 РИОС2;
- площадь треугольника С1 РИОС2;
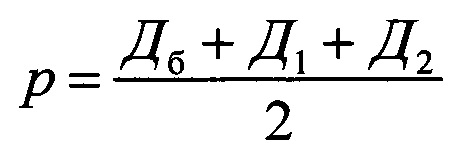 - полупериметр этого треугольника;
- полупериметр этого треугольника;
 - расстояние между ПП (фиг. 2).
- расстояние между ПП (фиг. 2).
Здесь индексы 1, 2 означают принадлежность к первой и второй ПП соответственно.
Если подставить выражения (4) в (2), то получим зависимость СКО σц от прямоугольных координат РИО и ЛА. Для нахождения аналитического выражения градиента целевой функции необходимо взять частные производные  и
и  . Опуская промежуточные выкладки, окончательно получим:
. Опуская промежуточные выкладки, окончательно получим:

где Δx1, Δz1 и Δx2, Δz2 - разности прямоугольных координат первого и второго ЛА соответственно и РИО:

После подстановки частных производных (5) и (6) в (3) можно вычислить значения для угла ψ2г.
Отметим, что при выполнении вычислительных операций по нахождению требуемого значения курса ψ2г в формулы (5), (6) необходимо подставлять полученные результаты измерений прямоугольных координат летательных аппаратов и сформированные в вычислительной системе 13 (фиг. 1) оценки прямоугольных координат zц, хц РИО и расстояний Д1 и Д2.
Алгоритм (3) траекторного управления вторым ЛА обеспечивает получение наибольшей скорости убывания среднего квадрата ошибки местоопределения РИО и, тем самым, удовлетворяет предъявленным требованиям. Достоинство данного алгоритма состоит в том, что убывание среднего квадрата ошибки местоопределения радиоизлучающей цели обеспечивается не только за счет изменения угла αц, как в различных вариантах ортогонального способа наведения, но и в результате целенаправленного уменьшения расстояния Д2. В то же время рассматриваемый градиентный способ управления не учитывает ограничения на траекторию движения второго ЛА при выходе его в опасную для полетов зону.
Для оценки принадлежности местоположения второго ЛА к опасной либо безопасной зонам необходимо знать расстояние от него до опасной зоны. В качестве примера опасной зоны для полетов второго ЛА рассмотрим область пространства вокруг РИО, представляющую круг с известным радиусом Д20, центр которой совпадает с РИО. В этой зоне полет второго ЛА по соображениям безопасности считается недопустимым. Следовательно, ЛА С2 не должен приближаться к РИО на расстояние, меньшее, чем Д20.
Расстояние ΔД до опасной зоны, отсчитываемое по линии, соединяющей РИО и второй ЛА, между вторым ЛА и окружностью с радиусом Д20, центр которой совпадает с РИО, рассчитывается по формуле:

Второй ЛА находится в безопасной зоне при условии, что ΔД>0, на границе опасной зоны при ΔД=0 и внутри опасной зоны при ΔД<0.
После выхода второго ЛА в район опасной зоны полета необходимо перейти с градиентного на другой способ наведения, учитывающий имеющиеся ограничения на траекторию полета второго ЛА, задаваемые допустимой областью нахождения второго ЛА. В этом случае алгоритмы траекторного управления могут быть найдены на основе способа проекции градиента целевой функции [Меркулов В.И., Миляков Д.А., Чернов B.C. Градиентные методы траекторного управления летательными аппаратами в двухпозиционной пассивной системе наведения воздушного базирования с повышенной точностью определения местоположения источников радиоизлучения // Информационно-измерительные и управляющие системы, 2015, т. 13, №5, стр. 17-22].
В общем случае под допустимой областью G понимается область n-мерного пространства, в которой выполняются ограничения, наложенные на переменные xi, i=1,2,…,n. В начальный момент времени второй ЛА находится в допустимой области G.
В случае выхода на границу области G в некоторой граничной точке х(k), k=0,1,2,…, движение в направлении антиградиента - ∇q(x(k)) может вывести ЛА за пределы допустимого множества. Поэтому антиградиент проецируется на линейное многообразие М, аппроксимирующее участок границы в окрестности точки х(k). Двигаясь в направлении проекции вектора -∇q(x(k)) на многообразие М, отыскивают новую точку х(k+1), в которой q(x(k+1))<q(x(k)), принимают х(к+1) за исходное приближение и продолжают процесс.
Для выбранного примера опасной зоны в виде круга с радиусом Д20, центр которой совпадает с РИО, допустимая область G для ЛА С2 может быть охарактеризована ограничением-неравенством вида
Д 20-Д2≤0.
Для случая ограничений подобного типа в [Меркулов В.И., Миляков Д.А., Чернов B.C. Градиентные методы траекторного управления летательными аппаратами в двухпозиционной пассивной системе наведения воздушного базирования с повышенной точностью определения местоположения источников радиоизлучения // Информационно-измерительные и управляющие системы, 2015, т. 13, №5, стр. 17-22] на основе способа проекции градиента получен алгоритм траекторного управления, в котором требуемый курс полета ЛА С2 рассчитывается по формуле

Здесь  - составляющие вектора проекции антиградиента в прямоугольной системе координат ZOX, в которых
- составляющие вектора проекции антиградиента в прямоугольной системе координат ZOX, в которых

Частные производные  и
и  целевой функции σц, входящие в выражения для составляющих d1 и d2, определяются соотношениями (5) и (6) соответственно.
целевой функции σц, входящие в выражения для составляющих d1 и d2, определяются соотношениями (5) и (6) соответственно.
После подстановки частных производных (5) и (6) в (8) требуемое значение угла ψ2пг может быть окончательно представлено в следующем виде:
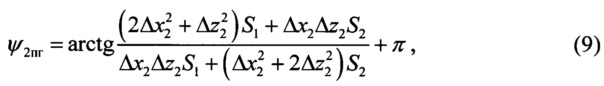
где 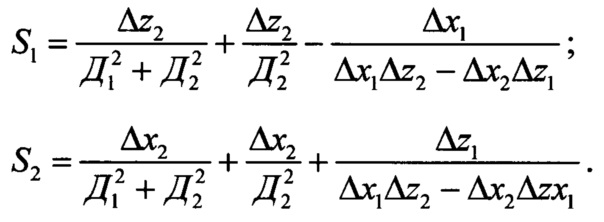
Алгоритм (9) позволяет рассчитывать требуемое направление полета ЛА, соответствующее положению вектора проекции антиградиента в точке текущего местоположения второго ЛА. Однако способ проекции градиента с использование (9) обладает существенным недостатком.
Спецификой алгоритма (9) является тот факт, что для всех пространственных точек, находящихся на луче, проходящем через РИО и точку текущего местоположения ЛА, значения требуемого курса ψ2пг являются одинаковыми. При этом полет ЛА будет осуществляться по окружности, радиус которой определяется значением расстояния между РИО и ЛА в текущий момент управления по способу проекции градиента. В общем случае значение этого радиуса может быть не равно Д20.
Объясняется это тем, что даже при условии начала управления по способу проекции градиента в точке, где выполняется равенство Д20-Д2=0, второй ЛА в силу свойственной ему инерционности может выйти из допустимой области и оказаться в опасной зоне. Аналогичная ситуация может сложиться в результате воздействия и других дестабилизирующих факторов, например из-за воздействия ветра на ЛА при наведении его на наземный РИО.
Таким образом, особенность способа проекции градиента состоит в том, что он в принципе позволяет определять направление требуемого движения ЛА в точке пересечения луча, проходящего через РИО и точку текущего местоположения ЛА, с окружностью радиуса Д20, но не обеспечивает при этом вывода ЛА в данную точку, находящуюся на границе опасной зоны. Поэтому необходимо иметь такой алгоритм траекторного управления, который бы одновременно обеспечивал также движение второго ЛА по границе опасной зоны полета, представляющей собой перемещающийся в пространстве синхронно с РИО круг с заданным радиусом Д20. Подобный алгоритм траекторного управления должен включать две составляющие. Первая составляющая, формируемая на основе способа проекции градиента, должна задавать требуемое направление движения второго ЛА по окружности заданного радиуса Д20, а вторая составляющая - обеспечивать удержание ЛА на самой окружности при движении по ней.
Модификация способа проекции градиента сводится к следующему.
Для движения ЛА по границе опасной зоны применительно к рассматриваемой ситуации параметр управления при полете по окружности целесообразно задавать в виде:

где ΔД - расстояние до опасной зоны, определяемое выражением (7);
 - скорость изменения этого расстояния во времени;
- скорость изменения этого расстояния во времени;
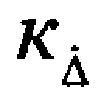 - весовой коэффициент.
- весовой коэффициент.
Второе слагаемое в (10) необходимо для повышения точности и устойчивости управления ЛА на траектории.
По существу расстояние ΔД характеризует боковое отклонение ЛА от окружности с радиусом Д20, отсчитываемое по линии, соединяющей центр окружности и второй ЛА.
Для реализации алгоритма (10) необходимо оценивать ΔД и 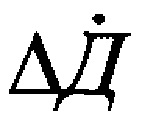 . Оценки расстояния от второго ЛА до центра окружности и скорости его изменения во времени вырабатываются в вычислительной системе ЛА в процессе реализации операций оценивания расстояний от РИО до ЛА, методика выполнения которых подробно изложена в [Верба B.C., Меркулов В.И., Дрогалин В.В. и др. Оценивание дальности и скорости в радиолокационных системах. Ч. 3 / Под ред. B.C. Вербы, В.И. Меркулова. - М.: «Радиотехника», 2010, стр. 382-396].
. Оценки расстояния от второго ЛА до центра окружности и скорости его изменения во времени вырабатываются в вычислительной системе ЛА в процессе реализации операций оценивания расстояний от РИО до ЛА, методика выполнения которых подробно изложена в [Верба B.C., Меркулов В.И., Дрогалин В.В. и др. Оценивание дальности и скорости в радиолокационных системах. Ч. 3 / Под ред. B.C. Вербы, В.И. Меркулова. - М.: «Радиотехника», 2010, стр. 382-396].
В соответствии со способом проекции градиента параметр управления ЛА, характеризующий несоответствие требуемого и фактического курсов, определяется выражением

в котором ψ2пг - требуемое значение курса, рассчитываемое по формуле (9);
ψ 2 - текущее значение курса второго ЛА.
Объединяя (11) и (12), для участка полета ЛА в районе границы опасной зоны и внутри ее, окончательно получим:

где κпг - весовой коэффициент по курсу;
κ м - весовой коэффициент по боковому отклонению и скорости его изменения.
Следует отметить, что численные значения весовых коэффициентов κпг, 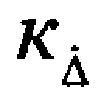 и κм подбирают заранее при моделировании процесса наведения ЛА, чтобы обеспечить заданные показатели эффективности функционирования УДПРЛС.
и κм подбирают заранее при моделировании процесса наведения ЛА, чтобы обеспечить заданные показатели эффективности функционирования УДПРЛС.
Алгоритм (12) обеспечивает реализацию предложенного способа решения задачи траекторного управления наблюдением, начиная с момента достижения границы опасной зоны вторым ЛА. Данный способ назовем модифицированным способом проекции градиента.
В свою очередь полет ЛА до границы опасной зоны осуществляется по градиентному способу в соответствии с алгоритмом (3).
Параметры управления (3) и (12) используют для изменения направления движения вторым ЛА в горизонтальной плоскости. Для этого параметр управления подают в канал бокового управления системы автоматического управления 14 (фиг. 1) второго ЛА, где он суммируется с сигналами, обеспечивающими повышение устойчивости и стабилизацию углового положения ЛА 15 в пространстве. Операция преобразования параметра управления в отклонение рулевых органов ЛА является стандартной и приведена, например, в [Авиационные системы радиоуправления. Т. 2. Радиоэлектронные следящие системы / Под ред. А.И. Канащенкова, В.И. Меркулова. - М.: «Радиотехника», 2003, стр. 337-339].
Для оценки качества и эффективности функционирования предложенных алгоритмов траекторного управления вторым ЛА на основе модифицированного способа проекции градиента было проведено математическое моделирование на ЭВМ процесса наведения летательных аппаратов. Частные результаты имитационного моделирования процесса наведения ЛА приведены на фиг. 4. В качестве гипотетических начальных условий выбраны: координаты первого ЛА z1=0 км, х1=0 км, скорость первого ЛА V1=800 м/с; координаты второго ЛА z2=0 км, х2=200 км, скорость второго ЛА V2=800 м/с; координаты РИО zц=200 км, хц=100 км, скорость РИО Vц=300 м/с. Первый ЛА наводится по методу пропорционального наведения, РИО движется прямолинейно. Радиус опасной зоны - Д20=150 км. Наведение ЛА на РИО осуществляется в заднюю полусферу.
На фиг. 4 введены следующие обозначения. ЛА1 - первый ЛА; ЛА2 - второй ЛА; РИО - радиоизлучающий объект. На фиг. 4, а отображены траектории движения двух ЛА и РИО, где буквами обозначены начальные положения объектов, а векторами - их скорости. На фиг. 4, б приведена зависимость Д2/Д20 отношения Д2 расстояния от второго ЛА до РИО к радиусу Д20 опасной зоны от времени. На фиг. 4, в показана зависимость СКО определения координат РИО σц от времени при условии, что угловая ошибка σα=15'. Фиг. 4, г иллюстрирует график изменения угла αц триангуляционного треугольника от времени, который приближается к αц≈90°, что и обеспечивает уменьшение СКО (2) определения местоположения РИО, иллюстрируемого фиг. 4, в.
Как видно из фиг. 4, б, приблизительно в момент времени t=215 с второй ЛА приближается на опасное расстояние Д20=150 км к РИО, после чего, в отличие от наведения по градиентному способу, начинает двигаться таким образом, чтобы не входить в опасную зону. На фигурах 4, а, 4, б и 4, г данный момент можно отличить по характерному излому соответствующих кривых. На фиг. 4, а видно, что после перехода второго ЛА на наведение по модифицированному способу проекции градиента он начинает двигаться по траектории, близкой к окружности с радиусом Д20, центр которой перемещается вместе с РИО. Из фиг. 4, б следует, что второй ЛА достаточно точно выдерживает границу опасной зоны. Фиг. 4, в демонстрирует уменьшение ошибки местоопределения РИО в процессе наведения.
Результаты экспериментальных исследований предложенного способа управления подтверждают возможность значительного улучшения точности оценивания координат и параметров движения РИО, что повышает эффективность применения угломерной двухпозиционной системы наведения в тактических ситуациях с существованием опасных зон полета. При наведении по модифицированному алгоритму проекции градиента наблюдается устойчивый полет второго ЛА вдоль границы опасной зоны.
Таким образом, предложенный способ управления летательными аппаратами по курсу в УДПРЛС обеспечивает решение задачи оптимизации взаимного положения наводимых ЛА и РИО, направленной на минимизацию ошибок оценивания координат и параметров движения РИО для любого момента времени, при наличии ограничений на траектории полетов второго ЛА. Использование заявленного способа, разработанного на основе концепции траекторного управления наблюдением, обеспечивает существенное повышение живучести угломерной двухпозиционной радиолокационной системы наведения за счет предотвращения входа второго ЛА в опасную зону. Тем самым, снимаются ограничения на тактические ситуации, присущие прототипу.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ ПО КУРСУ В УГЛОМЕРНОЙ ДВУХПОЗИЦИОННОЙ РАДИОЛОКАЦИОННОЙ СИСТЕМЕ | 2006 |
|
RU2308093C1 |
| СПОСОБ НАВЕДЕНИЯ ЛЕТАТЕЛЬНЫХ АППАРАТОВ НА ИСТОЧНИК РАДИОИЗЛУЧЕНИЯ В ДВУХПОЗИЦИОННОЙ ПАССИВНОЙ РАДИОЛОКАЦИОННОЙ СИСТЕМЕ | 2004 |
|
RU2262649C1 |
| СПОСОБ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ ПО КУРСУ В УГЛОМЕРНОЙ ДВУХПОЗИЦИОННОЙ РАДИОЛОКАЦИОННОЙ СИСТЕМЕ | 2004 |
|
RU2256870C1 |
| ИНФОРМАЦИОННО-ВЫЧИСЛИТЕЛЬНАЯ СИСТЕМА БЕСПИЛОТНОГО САМОЛЕТА-ИСТРЕБИТЕЛЯ | 2010 |
|
RU2418267C1 |
| СПОСОБ КОМБИНИРОВАННОГО НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА | 2014 |
|
RU2586399C2 |
| СПОСОБ СКРЫТНОГО САМОНАВЕДЕНИЯ САМОЛЕТОВ НА ВОЗДУШНЫЕ ОБЪЕКТЫ | 2009 |
|
RU2408845C1 |
| УГЛОМЕРНО-КОРРЕЛЯЦИОННЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ НАЗЕМНЫХ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ | 2011 |
|
RU2458358C1 |
| СПОСОБ ТРАЕКТОРНОГО УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ С ОБЛЕТОМ ЗОН С НЕБЛАГОПРИЯТНЫМИ МЕТЕОРОЛОГИЧЕСКИМИ УСЛОВИЯМИ | 2011 |
|
RU2490170C2 |
| СПОСОБ ПЕРЕХВАТА ПРИОРИТЕТНОЙ ЦЕЛИ, ОБЕСПЕЧИВАЮЩИЙ СРЫВ НАВЕДЕНИЯ ИСТРЕБИТЕЛЕЙ СОПРОВОЖДЕНИЯ | 2020 |
|
RU2742737C1 |
| СПОСОБ САМОНАВЕДЕНИЯ ЛЕТАТЕЛЬНЫХ АППАРАТОВ НА ГИПЕРЗВУКОВЫЕ ЦЕЛИ | 2009 |
|
RU2408847C1 |
Изобретение относится к технике управления летательными аппаратами (ЛА) и может найти применение в системах наведения ЛА на радиоизлучающие воздушные объекты с использованием угломерных двухпозиционных радиолокационных систем. Техническим результат – расширение функциональных возможностей на основе оптимизации условий радиолокационного наблюдения радиоизлучающего объекта (РИО). Для этого на основе измерений пеленгов РИО на двух ЛА, прямоугольных координат и курсов ЛА, осуществления между ЛА взаимного обмена результатами измерений оценивают прямоугольные координаты РИО и расстояния до него от ЛА, выбирают первый ЛА и осуществляют его наведение на РИО одним из известных способов, находят боковое отклонение второго ЛА от границы опасной зоны, представляющей окружность с заданным радиусом, определяют местоположение второго ЛА относительно границы опасной зоны и формируют параметр управления второго ЛА согласно градиентному способу при нахождении второго ЛА в безопасной зоне и согласно модифицированному способу проекции градиента при его нахождении на границе или внутри опасной зоны, отклоняют органы управления второго ЛА по курсу с использованием соответствующих параметров управления для градиентного способа и модифицированного способа проекции градиента. 4 ил.
Способ управления летательными аппаратами по курсу в угломерной двухпозиционной радиолокационной системе, заключающийся в том, что измеряют значения пеленгов радиоизлучающего объекта (РИО) на двух летательных аппаратах (ЛА), выступающих в качестве первой и второй приемной позиции (ПП), прямоугольные координаты местоположения и курсы ЛА, между ЛА осуществляют взаимный обмен результатами измерений пеленгов РИО, прямоугольных координат ЛА и их курсов, оценивают прямоугольные координаты РИО и расстояния до РИО от ЛА, выбирают первый ЛА, осуществляют самонаведение первого ЛА на РИО, формируют параметр управления Δ2г вторым ЛА согласно градиентному способу, отличающийся тем, что дополнительно находят расстояние до опасной зоны ΔД, на основе полученной оценки расстояния ΔД определяют принадлежность текущего местоположения второго ЛА к опасной или безопасной зонам полетов, находят проекцию градиента ошибки местоопределения РИО на границу опасной зоны, рассчитывают требуемый курс ψ2пг полета второго ЛА вдоль границы опасной зоны, формируют параметр управления Δ2мпг вторым ЛА в соответствии с модифицированным способом проекции градиента для полета вдоль границы опасной зоны по соотношению:
 ,
,
где ψ2 - курс второго ЛА;
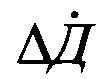 - производная ΔД по времени;
- производная ΔД по времени;
κпг - весовой коэффициент по курсу;
 - весовой коэффициент;
- весовой коэффициент;
κм - весовой коэффициент по расстоянию ΔД и скорости его изменения,
и отклоняют органы управления второго ЛА по курсу с использованием параметра управления Δ2г для градиентного способа при нахождении второго ЛА в безопасной зоне и соответственно параметра управления Δ2мпг для модифицированного способа проекции градиента при нахождении ЛА на границе или внутри опасной зоны.
| Меркулов В.И., Чернов B.C | |||
| Анализ методов наведения двухпозиционными пассивными системами воздушного базирования на источники радиоизлучения // Успехи современной радиоэлектроники, 2013, 7, стр | |||
| Скоропечатный станок для печатания со стеклянных пластинок | 1922 |
|
SU35A1 |
| СПОСОБ КОМАНДНОГО НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА НА НАЗЕМНЫЕ ЦЕЛИ | 2009 |
|
RU2408846C1 |
| Верба B.C., Меркулов В.И., Дрогалин В.В | |||
| и др | |||
| Оценивание дальности и скорости в радиолокационных системах | |||
| Ч | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| B.C | |||
| Вербы, В.И | |||
| Меркулова | |||
| - М.: "Радиотехника", 2010, стр | |||
| Зеркальный стереовизир | 1922 |
|
SU382A1 |
| УСТРОЙСТВО СОПРОВОЖДЕНИЯ МАНЕВРИРУЮЩЕЙ ЦЕЛИ | 2004 |
|
RU2292061C2 |
| Ботуз С.П | |||
| Позиционные системы программного управления подвижными объектами | |||
| - М.: ИПРЖ "Радиотехника", 1998 | |||
| Выбрасывающий ячеистый аппарат для рядовых сеялок | 1922 |
|
SU21A1 |
| АППАРАТУРА ПРИЕМА И РЕАЛИЗАЦИИ ЦЕЛЕУКАЗАНИЯ | 2002 |
|
RU2236666C2 |
Авторы
Даты
2018-07-09—Публикация
2017-03-15—Подача