Известна техническая и математическая модель искусственного нейрона [1-4]. Первая модель предложена в работе [1]. Позже [2], на основе таких моделей нейронов, реализованы первые искусственные нейронные сети (персептроны) для решения задач распознавания изображений букв. Подобные искусственные нейроны используются в качестве функциональной единицы всех современных искусственных нейронных сетей [3, 4] и представляют собой устройства с несколькими входами и одним выходом. Входные сигналы, поступая на входы, перемножаются с соответствующими весовыми коэффициентами, суммируются и преобразуются функцией передачи, в качестве которой может использоваться пороговая, линейная, сигмоидальная, гиперболическая и др. [3, 4]. Такая модель нейрона позволяет, хотя и достаточно грубо, воспроизводить некоторые из функций естественного нейрона. Объединяя искусственные нейроны в слои и сети, в совокупности с алгоритмами обучения, можно добиться приемлемого решения нейронной сетью сложных задач, не поддающихся адекватной формализации [3, 4].
Известна модель простейшего персептронного нейрона с двумя входами, парой весовых коэффициентов, сумматором и активационным блоком [3, 4]. Достоинством такой модели является возможность реализации ею большинства логических булевых функций. Так, для двух переменных, согласно [5], существует набор из 16 функций алгебры логики.
Наиболее близкой по техническим возможностям к предлагаемой модели нейрона является модель простейшего персептронного нейрона с двумя входами, парой весовых коэффициентов, сумматором и активационным блоком [6], устраняющая проблемы нереализуемости логической функции неравнозначности. Модель нейрона, реализующая логическую функцию неравнозначности, содержащая два входа, сигналы x1 и x2, принимающие значения 0 или 1, с которых перемножаются с соответствующими весовыми коэффициентами ω1 и ω2, где ω1=1, а ω2=-1,и поступают на сумматор, причем s∈(-l, 0, 1), где s - сумма с выхода сумматора, s=x1ω1+x2ω2, отличающаяся тем, что сумма s преобразуется в активационном блоке модульной функцией активации вида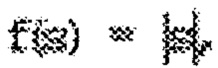 а затем пороговой функцией
а затем пороговой функцией
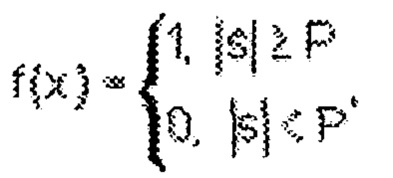
где Р - величина порога, Р=0,5, f(x) - функция на выходе нейрона. Данная модель устраняет проблемы нереализуемости логической функции неравнозначности, оставляя нерешенным вопрос разделения линейно неразделимых классов объектов. Однако она, как и все перечисленные выше модели выполняет функцию линейного разделения классов с помощью гиперплоскости, построенной в многомерном континуальном пространстве.
Предлагаемый способ управления реакцией нейропроцессора (НП) на входные сигналы направлен на устранение рассмотренного недостатка (проблемы разделения линейно неразделимых классов объектов) известных моделей нейрона. Аппроксимация многомерных функций позволяет учитывать нелинейные свойства поверхности разделения классов объектов в N-мерном континуальном пространстве. На основе экспериментальных или теоретических данные о поведении НП в заданных точках многомерного континуального пространства его параметры настраиваются путем обучения на исчисление реакции во всей области поиска решений.
В патентуемом способе управления реакцией нейронного процессора (НП) на входные сигналы (стимулы) x1, x2,…, xN в каждую ячейку запоминающего устройства (ЗУ) НП записывают кортеж значений параметров 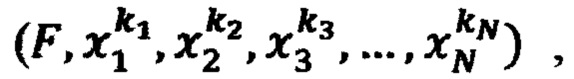 где F - фиксированное значение реакции НП на комбинацию значений стимулов
где F - фиксированное значение реакции НП на комбинацию значений стимулов 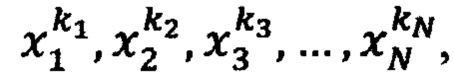 комбинации значений стимулов в ЗУ получают перебором значений каждого воздействия xi из возрастающей последовательности фиксированных значений
комбинации значений стимулов в ЗУ получают перебором значений каждого воздействия xi из возрастающей последовательности фиксированных значений 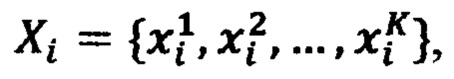 где K - количество фиксированных значений стимулов xi, из соседних значений последовательности Xi в ЗУ образуют K-1 интервалов по каждому стимулу, перебором интервалов по всем переменным x1, x2, …, xN образуют (K-1)N подобластей Ω* в области Ω определения реакции НП F(x1, x2, …, хN), на N входов НП подают стимулы
где K - количество фиксированных значений стимулов xi, из соседних значений последовательности Xi в ЗУ образуют K-1 интервалов по каждому стимулу, перебором интервалов по всем переменным x1, x2, …, xN образуют (K-1)N подобластей Ω* в области Ω определения реакции НП F(x1, x2, …, хN), на N входов НП подают стимулы 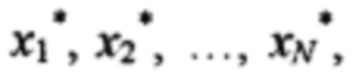 определяют принадлежность поданных сигналов некоторой подобласти Ω*, ограниченной интервалами
определяют принадлежность поданных сигналов некоторой подобласти Ω*, ограниченной интервалами 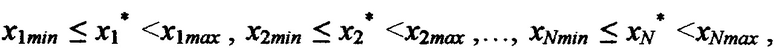 где x1min, x1max, x2min, x2max, …, xNmin, xNmax - ближайшие значения стимулов из последовательностей Xi, i изменяется от 1 до N, в интервале (x1min, x1max) вычисляют 2N-1 интерполирующих значений реакции НП (ИЗРН) F по формуле
где x1min, x1max, x2min, x2max, …, xNmin, xNmax - ближайшие значения стимулов из последовательностей Xi, i изменяется от 1 до N, в интервале (x1min, x1max) вычисляют 2N-1 интерполирующих значений реакции НП (ИЗРН) F по формуле
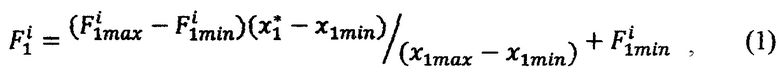
где i - номер промежуточного ИЗРН F на первом шаге вычисления, 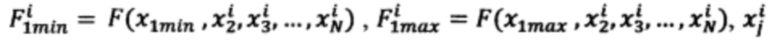 - крайние значения стимулов, ограничивающие выбранную подобласть Ω* в N-мерной области определения реакции НП,
- крайние значения стимулов, ограничивающие выбранную подобласть Ω* в N-мерной области определения реакции НП,

на j-м шаге в интервале [xjmin, Xjmax) вычисляют 2N-j ИЗРН F по формуле
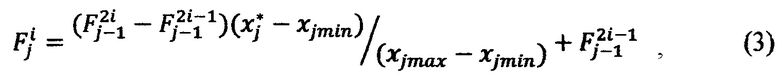
где i - номер промежуточного ИЗРН на j-м шаге (j изменяется от 2 до N), на N-м шаге в интервале [хNmin, xNmax) при j=N по формуле (3) вычисляют искомое значение реакции НП 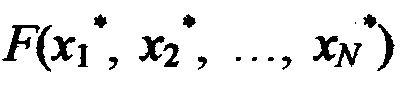 на сигналы
на сигналы 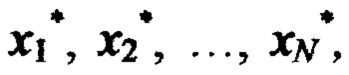 для настройки НП в каждую ячейку ЗУ записывают кортежи значений параметров
для настройки НП в каждую ячейку ЗУ записывают кортежи значений параметров 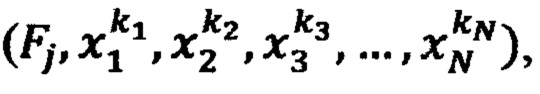 где
где 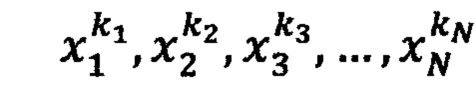 - комбинация заданных значений стимулов, получаемая для каждого стимула xi из возрастающей последовательности
- комбинация заданных значений стимулов, получаемая для каждого стимула xi из возрастающей последовательности 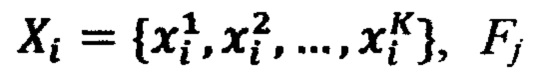 - начальное значение реакции НП при заданных значениях стимулов, формируют обучающие кортежи
- начальное значение реакции НП при заданных значениях стимулов, формируют обучающие кортежи 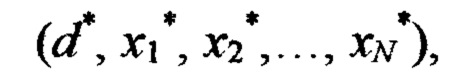 состоящих из эталонного сигнала d* и соответствующих ему стимулов
состоящих из эталонного сигнала d* и соответствующих ему стимулов 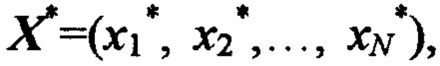 на обучающий вход НП поочередно подают эталонные сигналы d1, d2, … dS, образующие обучающую выборку (эпоху), а на сигнальные входы НП подают соответствующие каждому эталонному сигналу d∈{d1, d2,… dS} стимулы х1, х2,…, хN, эталонные сигналы выбирают так, чтобы в каждой подобласти Ω*∈Ω находился хотя бы один обучающий кортеж, при подаче очередного эталонного сигнала d*∈{d1, d2,… dS} и стимулов
на обучающий вход НП поочередно подают эталонные сигналы d1, d2, … dS, образующие обучающую выборку (эпоху), а на сигнальные входы НП подают соответствующие каждому эталонному сигналу d∈{d1, d2,… dS} стимулы х1, х2,…, хN, эталонные сигналы выбирают так, чтобы в каждой подобласти Ω*∈Ω находился хотя бы один обучающий кортеж, при подаче очередного эталонного сигнала d*∈{d1, d2,… dS} и стимулов 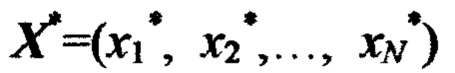 определяют подобласть Ω*, внутри которой находится обучающий кортеж
определяют подобласть Ω*, внутри которой находится обучающий кортеж 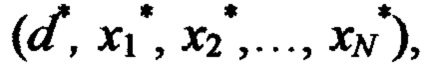 вычисляют реакцию F* НП на стимулы
вычисляют реакцию F* НП на стимулы 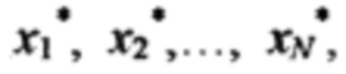 вычисляют невязку е*=d*-F*, выполняют пошаговое вычисление невязок в вершинах параллелепипеда, ограничивающего подобласть Ω*, для этого на первом шаге вычисляют невязку в точке
вычисляют невязку е*=d*-F*, выполняют пошаговое вычисление невязок в вершинах параллелепипеда, ограничивающего подобласть Ω*, для этого на первом шаге вычисляют невязку в точке 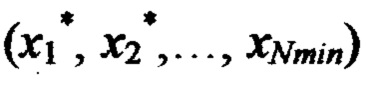 по формуле
по формуле 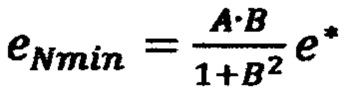 и невязку в точке
и невязку в точке 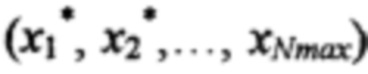 по формуле
по формуле 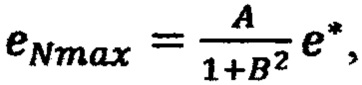 где
где 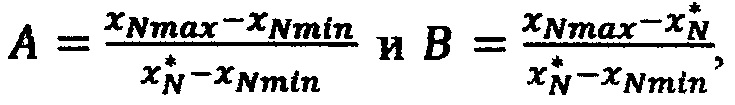 на втором шаге вычисляют невязку в точке
на втором шаге вычисляют невязку в точке 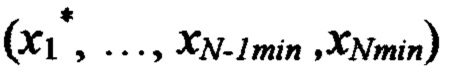 по формуле
по формуле 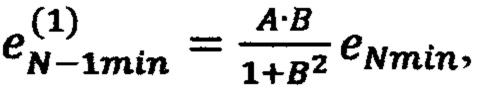 невязку в точке
невязку в точке 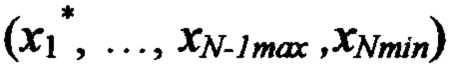 по формуле
по формуле 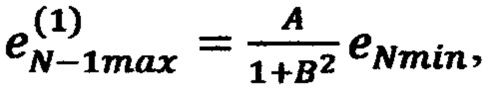 невязку в точке
невязку в точке 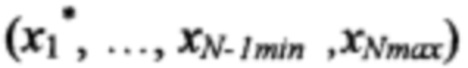 по формуле
по формуле 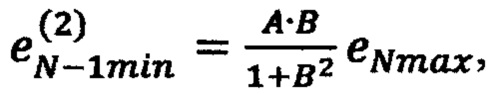 невязку в точке
невязку в точке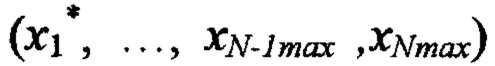 по формуле
по формуле 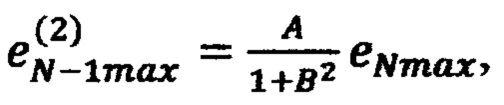 где
где  на третьем шаге вычисляют невязку в точке
на третьем шаге вычисляют невязку в точке 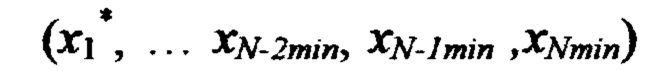 по формуле
по формуле 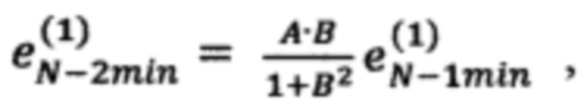 невязку в точке
невязку в точке 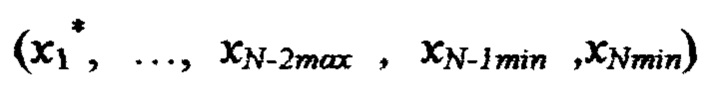 по формуле
по формуле 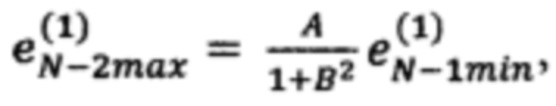 невязку в точке
невязку в точке 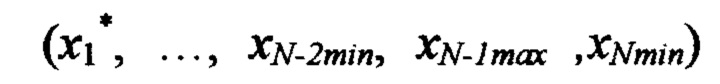 по формуле
по формуле 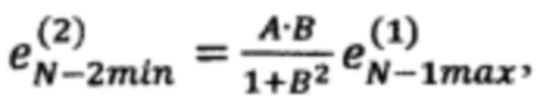 невязку в точке
невязку в точке 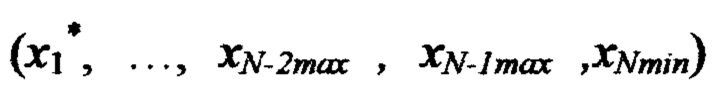 по формуле
по формуле 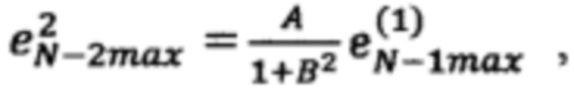 невязку в точке
невязку в точке 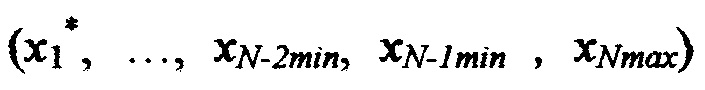 по формуле
по формуле 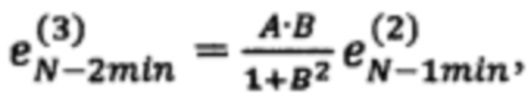 невязку в точке
невязку в точке 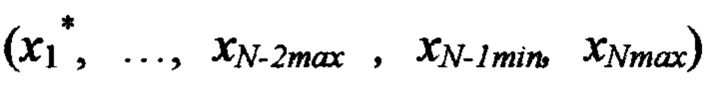 по формуле
по формуле 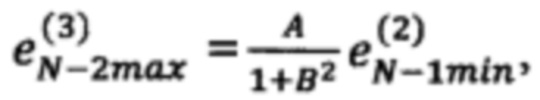 невязку в точке
невязку в точке 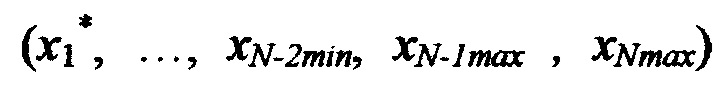 по формуле
по формуле 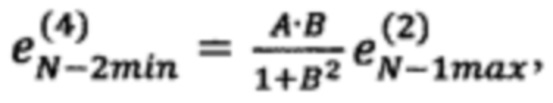 невязку в точке
невязку в точке 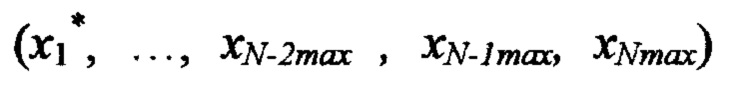 по формуле
по формуле 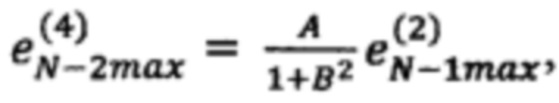 где
где 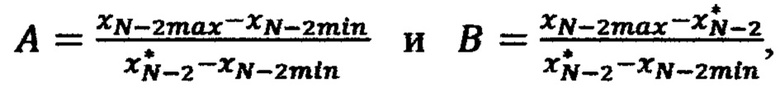 и так далее, продолжая вычисления, на N-м шаге рассчитывают невязку во всех 2N вершинах N-мерного параллелепипеда, ограничивающего подобласть значений Ω*, выполняют корректировку значений реакции F в ЗУ во всех 2N вершинах N-мерного параллелепипеда на величины рассчитанных в них невязок, процедуры расчета невязок и коррекции значений реакции НП F повторяют для всех эталонных обучающих сигналов d1, d2,… dS до тех пор, пока не будет достигнут приемлемое отклонение расчетных значений от эталонных в кортежах.
и так далее, продолжая вычисления, на N-м шаге рассчитывают невязку во всех 2N вершинах N-мерного параллелепипеда, ограничивающего подобласть значений Ω*, выполняют корректировку значений реакции F в ЗУ во всех 2N вершинах N-мерного параллелепипеда на величины рассчитанных в них невязок, процедуры расчета невязок и коррекции значений реакции НП F повторяют для всех эталонных обучающих сигналов d1, d2,… dS до тех пор, пока не будет достигнут приемлемое отклонение расчетных значений от эталонных в кортежах.
Рассмотрим вычисление реакции НП на примере с тремя входными сигналы. Перед началом работы процессора в ЗУ загружаются исходные значения управляющего сигнала (конечное дискретное множество Ψ четких значений функции F), которые получают на множестве Θ фиксированных опорных точек по результатам экспериментальных или теоретических исследований N-мерной функции F. Каждая фиксированная точка представлена в ЗУ кортежем 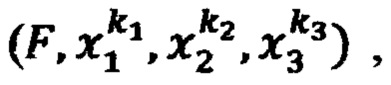 где F - выбранное значение реакции НП при исходных дискретных значениях стимулов
где F - выбранное значение реакции НП при исходных дискретных значениях стимулов 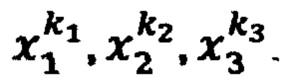 Комбинации значений стимулов в ЗУ получают перебором значений каждого стимула хi, из возрастающей последовательности фиксированных значений
Комбинации значений стимулов в ЗУ получают перебором значений каждого стимула хi, из возрастающей последовательности фиксированных значений 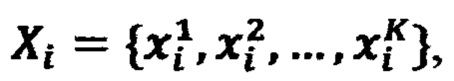 где K - количество фиксированных значений стимулов хi. Выбирая из последовательностей Х1, Х2 и Х3 соседние значения стимулов в ЗУ образуют K-1 интервалов по каждому стимулу. Комбинируя интервалы, образуют (К-1)3 подобластей Ω* в области Ω определения реакции НП F(x1, x2, x3) Если на входы НП поданы сигналы
где K - количество фиксированных значений стимулов хi. Выбирая из последовательностей Х1, Х2 и Х3 соседние значения стимулов в ЗУ образуют K-1 интервалов по каждому стимулу. Комбинируя интервалы, образуют (К-1)3 подобластей Ω* в области Ω определения реакции НП F(x1, x2, x3) Если на входы НП поданы сигналы 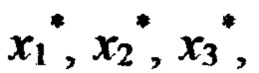 то определяется подобласть Ω*, ограниченная интервалом
то определяется подобласть Ω*, ограниченная интервалом 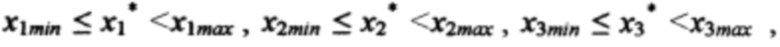 где x1min, x1max, x2min, x2max, x3min, x3max - ближайшее значения стимулов из последовательностей X1, Х2 и Х3.
где x1min, x1max, x2min, x2max, x3min, x3max - ближайшее значения стимулов из последовательностей X1, Х2 и Х3.
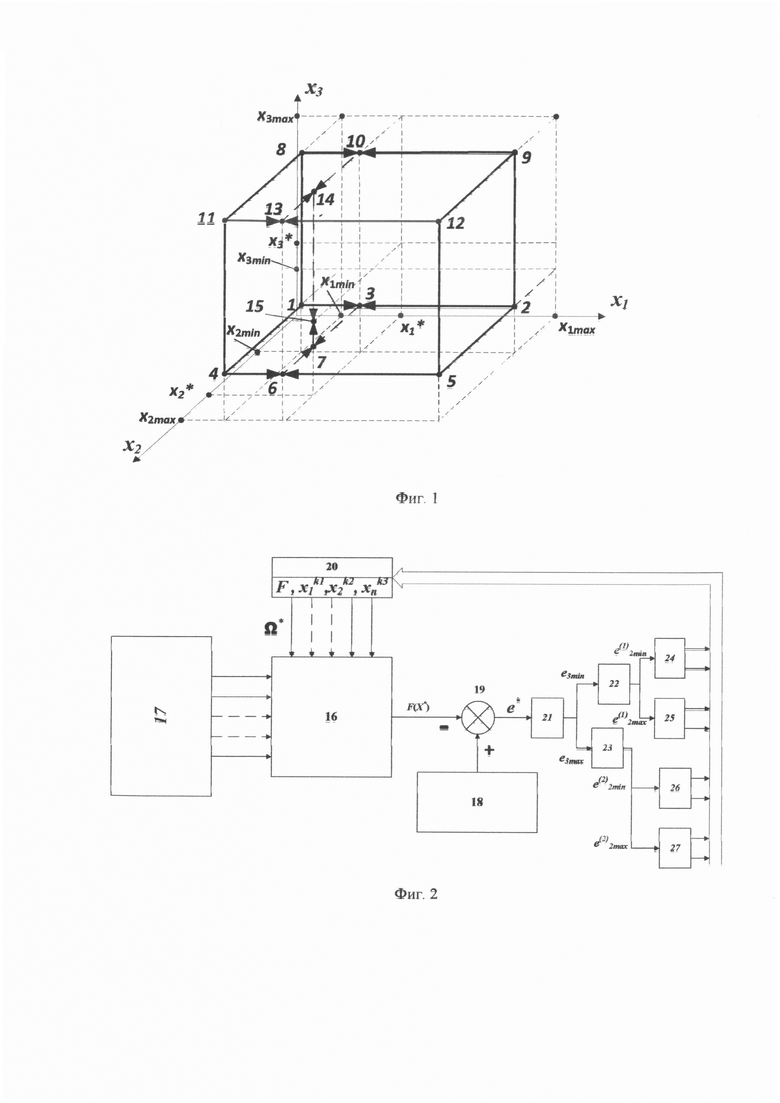
На фиг. 1 приведена иллюстрация порядка исчисления НП реакции при трех входных сигналах 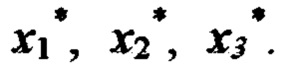 На первом этапе с помощью формулы (1) процессор рассчитывает промежуточные ИЗРН
На первом этапе с помощью формулы (1) процессор рассчитывает промежуточные ИЗРН 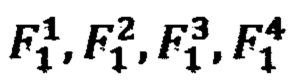 в точках 3, 6, 10, 13. Для расчета ИЗРН
в точках 3, 6, 10, 13. Для расчета ИЗРН 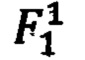 в точке 3 в формулу (1) подставляются значения функции в точках 1, 2 и координаты
в точке 3 в формулу (1) подставляются значения функции в точках 1, 2 и координаты 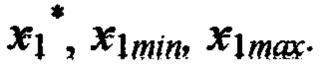 Для расчета
Для расчета 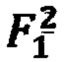 в точке 6 в формулу (1) подставляются значения функции в точках 4 и 5 и координаты
в точке 6 в формулу (1) подставляются значения функции в точках 4 и 5 и координаты 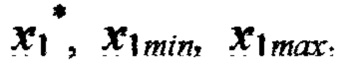 Для расчета
Для расчета 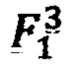 в точке 10 в формулу (1) подставляются значения функции в точках 8 и 9 и координаты
в точке 10 в формулу (1) подставляются значения функции в точках 8 и 9 и координаты  Для расчета
Для расчета 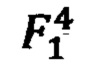 в точке 13 в формулу (1) подставляются значения функции в точках 11 и 12 и координаты
в точке 13 в формулу (1) подставляются значения функции в точках 11 и 12 и координаты 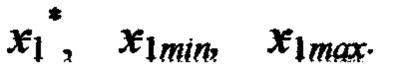 На втором этане, используя рассчитанные ранее промежуточные ИЗРН
На втором этане, используя рассчитанные ранее промежуточные ИЗРН 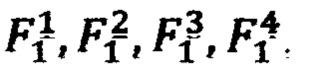
Для расчета ИЗРН 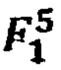 в точке 7 в формулу (3) подставляются значения ИЗРН
в точке 7 в формулу (3) подставляются значения ИЗРН 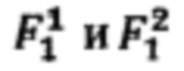 в точках 3, 6 и координаты
в точках 3, 6 и координаты 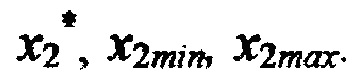 Для расчета ИЗРН
Для расчета ИЗРН 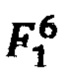 в точке 14 в формулу (3) подставляются значения ИЗРН
в точке 14 в формулу (3) подставляются значения ИЗРН 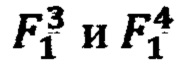 в точках 10, 13 и координаты
в точках 10, 13 и координаты 
На последнем этапе расчета вычисляется значение реакции НП на стимулы 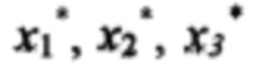 в точке 15 с координатами
в точке 15 с координатами 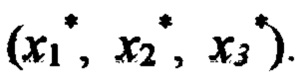 Для этого в формулу (3) подставляются значения ИЗРН
Для этого в формулу (3) подставляются значения ИЗРН 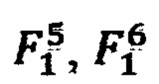 и координаты
и координаты 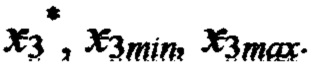
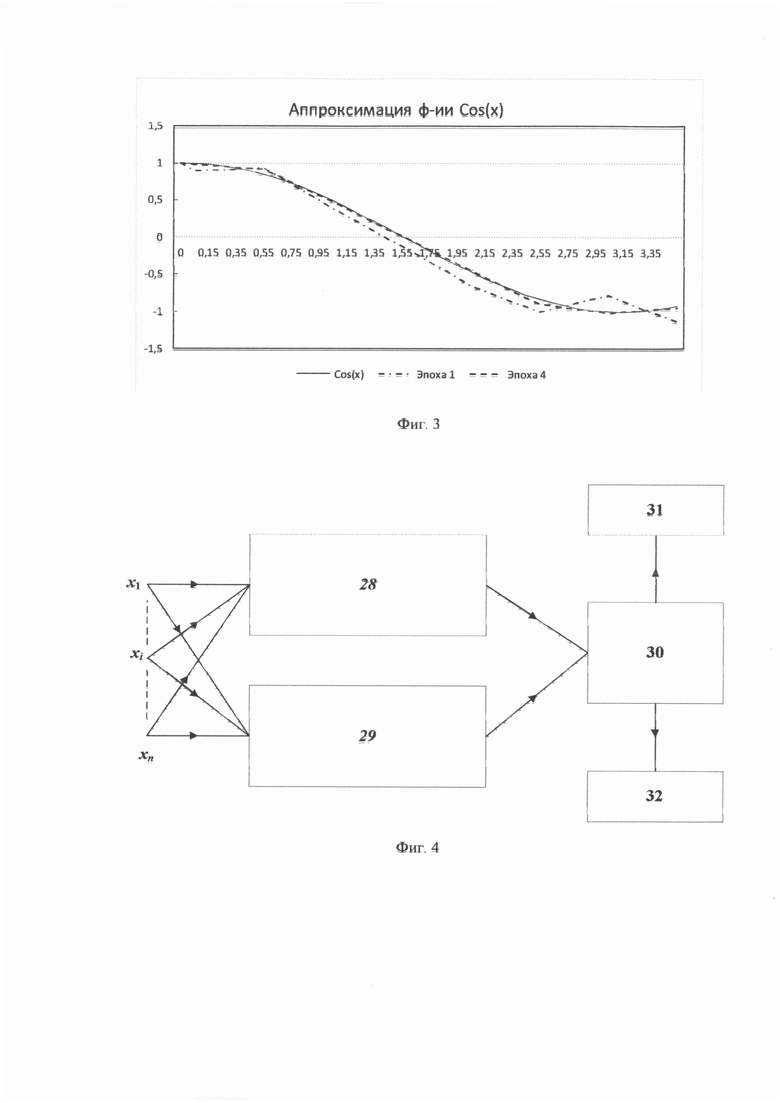
На том же примере (Фиг. 1) проиллюстрируем настройку (обучение) НП. Структура НП изображена на фиг. 2. Обучение выполняется путем подачи на входы расчетного блока 16 стимулов x1, x2, x3 17 и обучающих эталонных сигналов d1, d2, … dS 18 на сумматор 19.
Очередной i-й шаг обучения начинается с подачи эталонного сигнала d*∈{d1, d2, … dS} 18 и соответствующих ему значений стимулов 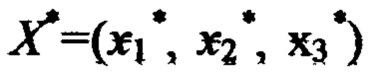 18. В расчетном блоке 16 по значениям стимулов и значениям фиксированных опорных точек из ЗУ 20 определяют точку 15 внутри одной из (K-1)N подобластей Ω* в области Ω определения функции F(x1, х2, х3). В расчетном блоке 16 определяется текущее значение реакции F(X*) НП на стимулы
18. В расчетном блоке 16 по значениям стимулов и значениям фиксированных опорных точек из ЗУ 20 определяют точку 15 внутри одной из (K-1)N подобластей Ω* в области Ω определения функции F(x1, х2, х3). В расчетном блоке 16 определяется текущее значение реакции F(X*) НП на стимулы  В сумматоре 19 вычисляется невязка е*=d*-F(X*) (точка 15 на Фиг. 1). Далее переходят к распространению невязок от точки X* к вершинам параллепипеда, ограничивающего подобласть Ω*. На первом шаге вычисляют (блок 21) невязку в точке 7 с координатами
В сумматоре 19 вычисляется невязка е*=d*-F(X*) (точка 15 на Фиг. 1). Далее переходят к распространению невязок от точки X* к вершинам параллепипеда, ограничивающего подобласть Ω*. На первом шаге вычисляют (блок 21) невязку в точке 7 с координатами 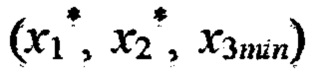 по формуле
по формуле 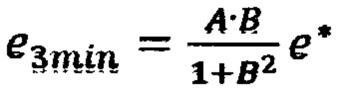 и невязку в точке 14 с координатами
и невязку в точке 14 с координатами 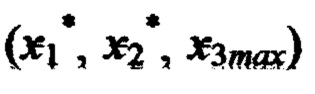 по формуле
по формуле 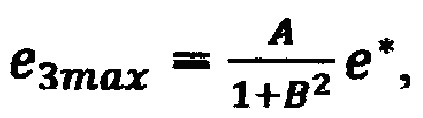 где
где 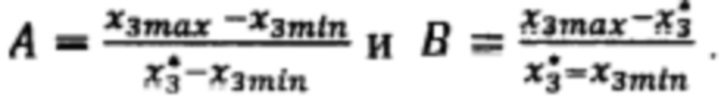
На втором шаге вычисляют невязку в точке 3 с координатами 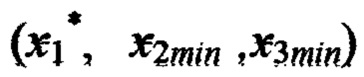 по формуле
по формуле 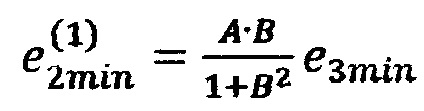 (блок 22), невязку в точке 6 с координатами
(блок 22), невязку в точке 6 с координатами 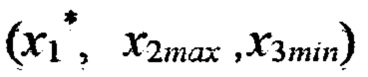 по формуле
по формуле 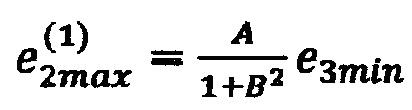 (блок 22), невязку в точке 10 с координатами
(блок 22), невязку в точке 10 с координатами  по формуле
по формуле 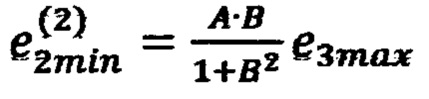 (блок 23), невязку в точке 13 с координатами
(блок 23), невязку в точке 13 с координатами 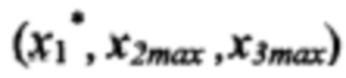 по формуле
по формуле 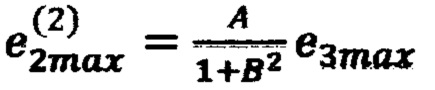 (блок 23), где
(блок 23), где 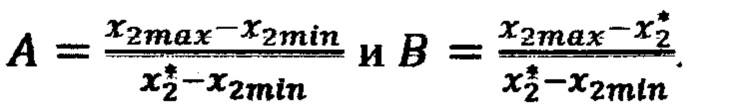
На третьем шаге вычисляют: невязку в точке 1 с координатами (x1min, x2min, x3min) по формуле 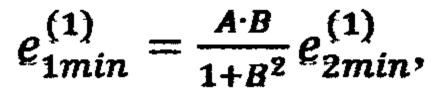 невязку в точке 2 с координатами (х1max, x2min,х3min) по формуле
невязку в точке 2 с координатами (х1max, x2min,х3min) по формуле 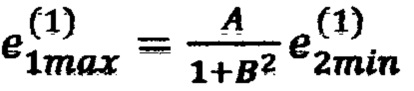 (блок 24), невязку в точке 4 с координатами (х1min, х2max, x3min) по формуле
(блок 24), невязку в точке 4 с координатами (х1min, х2max, x3min) по формуле 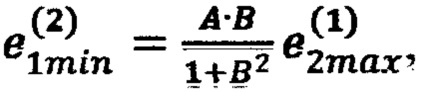 невязку в точке 5 с координатами (x1max, x2max, x3min) по формуле
невязку в точке 5 с координатами (x1max, x2max, x3min) по формуле 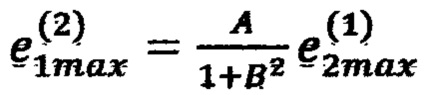 (блок 25), невязку в точке 8 c координатами (х1min, х2min, х3max) по формуле
(блок 25), невязку в точке 8 c координатами (х1min, х2min, х3max) по формуле 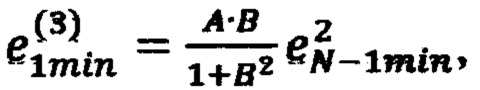 невязку в точке 9 с координатами (x1max, х2min, x3max) по формуле
невязку в точке 9 с координатами (x1max, х2min, x3max) по формуле 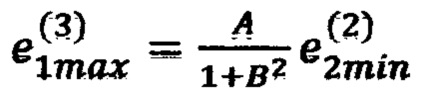 (блок 26), невязку в точке 11 с координатами (x1min, х2max, x3max) по формуле
(блок 26), невязку в точке 11 с координатами (x1min, х2max, x3max) по формуле 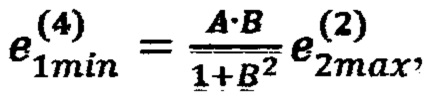 невязку в точке 12 с координатами (x1max, x2max, x3max) по формуле
невязку в точке 12 с координатами (x1max, x2max, x3max) по формуле 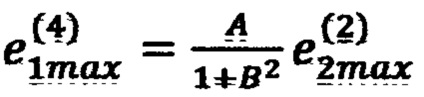 (блок 27), где
(блок 27), где 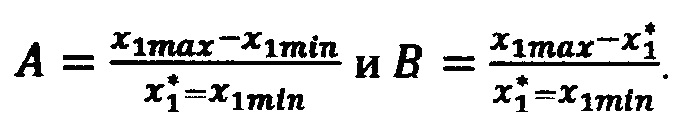
В результате проведенных вычислений на третьем шаге получены значения невязок во всех 8-ми вершинах куба, ограничивающего область Ω* попадания значений стимулов 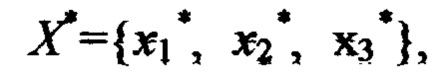 которые применяют для корректировки значений функции F в фиксированных опорных точках в ЗУ 20.
которые применяют для корректировки значений функции F в фиксированных опорных точках в ЗУ 20.
Применяемые в способе обучения НП формулы расчета невязок выбраны из условия минимизации невязок, распространяемых в вершины N-куба области Ω*.
Работу алгоритма обучения иллюстрирует пример аппроксимации с помощью НП функции Cos(x).
Обучение НП выполнялось в интервале значений аргумента [0, π]. Интервал обучения был разбит на семь равных отрезков. Внутри отрезков были заданы опорные (точные) значения функции, которые подавались на вход НП вместе с значениями переменной x в опорной точке. В исходном состоянии все опорные значения НП были обнулены.
Невязки рассчитывались внутри каждого интервала и передавалась на его края для коррекции значений опорных точек. В процессе обучения одной эпохи процедуры коррекция опорных значений выполнялись последовательно от самого левого отрезка интервала обучения к правому. После каждой эпохи обучения регистрировалась максимальная невязка НП с образцовыми значениями.
Процесс обучения показал хорошую сходимость. После 15-й эпохи ошибка аппроксимации стала менее 1% и продолжала уменьшатся. На фиг. 3 приведена иллюстрация аппроксимации функции COS после первой и четвертой эпох обучения.
НП может быть применена для классификации линейно неразделимых классов объектов.
Классический подход к классификации образов опирается на байесовскую теорию проверки гипотез. На входы байесовского классификатора поступают параметры вектора наблюдений 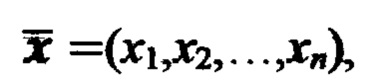 которые передаются на входы двух интерполирующих процессоров. Первый процессор аппроксимирует значения функции выбора класса C1:
которые передаются на входы двух интерполирующих процессоров. Первый процессор аппроксимирует значения функции выбора класса C1:
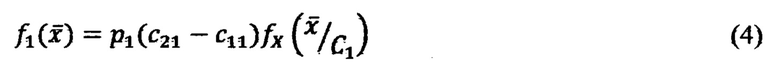
второй значения функции выбора класса С2:
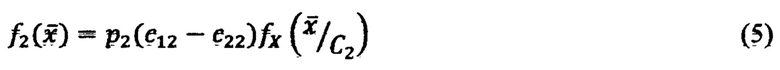
, где 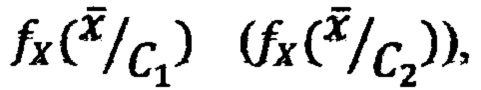 - функции плотности вероятности случайного вектора
- функции плотности вероятности случайного вектора  при условии, что он принадлежит пространству Х1 (Х2), параметры c11,c12, c21,c22, p1,p2 определяются условиями решаемой задачи [7]. НП позволяет строить нелинейные функции (4) и (5) в процессе обучения при подаче на вход НП обучающих сигналов. Структура устройства, выполняющего функцию разделения двух классов, показана на Фиг. 4.
при условии, что он принадлежит пространству Х1 (Х2), параметры c11,c12, c21,c22, p1,p2 определяются условиями решаемой задачи [7]. НП позволяет строить нелинейные функции (4) и (5) в процессе обучения при подаче на вход НП обучающих сигналов. Структура устройства, выполняющего функцию разделения двух классов, показана на Фиг. 4.
Устройство состоит из двух НП 28 и 29, выполняющих с помощью патентуемого способа исчисления значений реакции НП на подаваемые стимулы х1, х2,…, хn исчисление функций 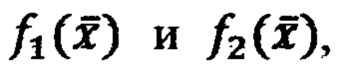 и компаратора 30 выполняющего сравнение значений. Если
и компаратора 30 выполняющего сравнение значений. Если 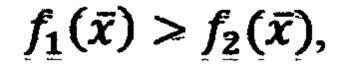 выбирается класс C1 31. В противном случае - класс С2 32.
выбирается класс C1 31. В противном случае - класс С2 32.
Таким образом, предлагаемая модель нейропроцессора, реализуя модель нелинейной разделяющей поверхности, преодолевает проблему разделения линейно неразделимых классов объектов. Предлагаемый способ позволяет распараллеливать вычисления значений функции, что создает возможности повышения скорости НП в десятки раз по сравнению с традиционной моделью на основе персептрона. В последнем случае НП должен быть выполнен на аналоговых схемах, которые не требуют аналогово-цифровых преобразований входных сигналов.
Источники информации
1. McGuIIoch W.S., Pitts W. A logical calculus of the ideas imminent in nervous activity. // Bulletin of Mathematical Biophysics, vol.5, 1943, pp.115-133. (Рус. перевод: Маккаллок У.С., Питтс У. Логическое исчисление идей, относящихся к нервной деятельности. Автоматы. / Под ред. К.Э.Шеннона, Дж.Маккарти. - М.: ИЛ, 1956).
2. Rosenblatt F. Principles of neurodinamics. Perceptrons and the theory of brain mechanisms. Spartan Books, Washington, 1962. (Рус.перевод: Розенблатт Ф. Принципы нейродинамики. Нерцептроны и теория механизмов мозга. / Под ред. С.М.Осовца. - М: Мир, 1965 - 480 с).
3. Галушкин А.И. Теория нейронных сетей. Кн. 1: Учеб. пособие для вузов / Общая ред. А.И.Галушкина. - М.: ИПРЖР, 2000. - 416 с.
4. Wasserman P. Neurocomputing. Theory and practice, Nostram Reinhold, 1990. (Рус. перевод: Уоссермен Ф. Нейрокомпьютерная техника: теория и практика. / Пер. с англ. Ю.А. уев, В.А.Точенов. - М.: Мир, 1992. - 240 с).
5. Куринной Г.Ч. Математика: Справочник. - Харьков: Фолио; Ростов н/Д: Феникс, 1997. - 463 с.
6. Самойлин Е. А. Патент RU №2269155 от 22.08.2003 МПК G06G 7/06 (2006.01) Модель нейрона, реализующая логическую функцию неравнозначности.
7. Осовский С.Нейронные сети для обработки информации. М.: Финансы и статистика, 2002. - 344 с.: ил.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ хранения и считывания аналоговых значений функций многих переменных | 2017 |
|
RU2656704C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ НЕЙРОНА | 2009 |
|
RU2402813C1 |
| ПОСТРОЕНИЕ НЕЙРОННОЙ СЕТИ НА ОСНОВЕ НЕЙРОНОВ С ФУНКЦИОНАЛЬНЫМ ПРЕОБРАЗОВАНИЕМ ПРОИЗВОЛЬНОГО ВИДА ДЛЯ ВХОДНЫХ СИГНАЛОВ | 2018 |
|
RU2727080C2 |
| СПОСОБ ОБУЧЕНИЯ ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ | 2014 |
|
RU2566979C1 |
| СПОСОБ КЛАССИФИКАЦИИ ЭЛЕКТРОЭНЦЕФАЛОГРАФИЧЕСКИХ СИГНАЛОВ В ИНТЕРФЕЙСЕ МОЗГ - КОМПЬЮТЕР | 2009 |
|
RU2415642C1 |
| СПОСОБ АДАПТИВНОЙ ПРОСТРАНСТВЕННО-ВРЕМЕННОЙ АНИЗОТРОПНОЙ БИЛАТЕРАЛЬНОЙ ФИЛЬТРАЦИИ ВИДЕОСИГНАЛОВ | 2007 |
|
RU2360287C1 |
| СПОСОБ ОБУЧЕНИЯ ГЛУБОКИХ НЕЙРОННЫХ СЕТЕЙ НА ОСНОВЕ РАСПРЕДЕЛЕНИЙ ПОПАРНЫХ МЕР СХОЖЕСТИ | 2016 |
|
RU2641447C1 |
| Способ диагностики острого коронарного синдрома | 2020 |
|
RU2733077C1 |
| СПОСОБ ОЦЕНИВАНИЯ ПАРАМЕТРОВ ТРАЕКТОРИИ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЙ В ДВУХПОЗИЦИОННОЙ УГЛОМЕРНОЙ РАДИОЛОКАЦИОННОЙ СИСТЕМЕ | 2003 |
|
RU2246121C9 |
| СПОСОБ ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ ОБЪЕКТОВ | 2017 |
|
RU2692420C2 |
Изобретение относится к нейрокибернетике и может быть использовано в качестве функциональной единицы различных искусственных нейронных сетей. Техническим результатом является устранение проблемы нереализуемости разделения нелинейно неразделимых классов известными моделями нейронов. Указанный результат достигается за счет того, что с учетом нелинейных свойств поверхности разделения классов объектов в N-мерном континуальном пространстве нейропроцессор (НП) выполняет линейную аппроксимацию функций в подобластях области Ω, а параметры нейропроцессора настраиваются путем обучения на основе экспериментальных или теоретических данных о поведении нейропроцессора в заданных точках N-мерного континуального пространства. При обучении нейропроцессора на обучающий вход поочередно подают эталонные сигналы d1, d2,…, ds, а на сигнальные входы НП подают соответствующие им стимулы х1, х2,…, xN. Эталонные сигналы выбирают так, чтобы в каждой подобласти Ω*∈Ω находилась хотя бы одна обучающая выборка. При повторении эпох выполняется минимизация погрешностей функции в вершинах N-мерного куба, ограничивающего каждую подобласть Ω*. 4 ил.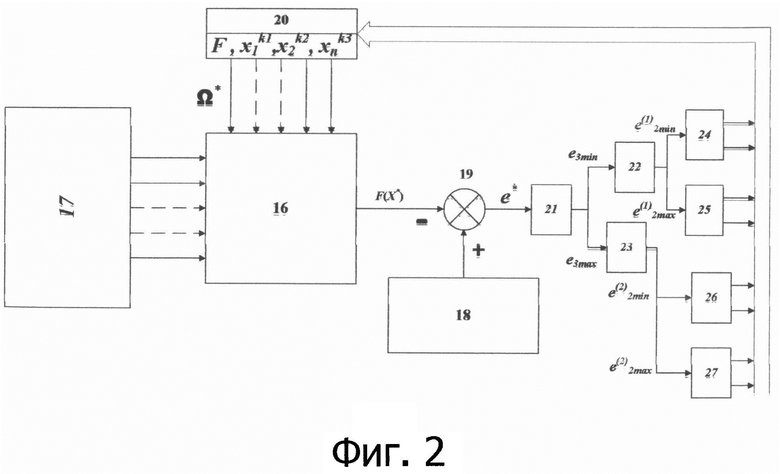
Способ управления реакцией нейропроцессора на входные сигналы (стимулы) x1, х2, …, хN, в котором в каждую ячейку запоминающего устройства (ЗУ) НП записывают кортеж значений параметров 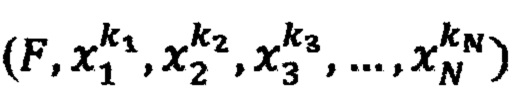 , где F - фиксированное значение реакции НП на комбинацию значений стимулов
, где F - фиксированное значение реакции НП на комбинацию значений стимулов 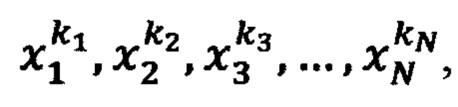 комбинации значений стимулов в ЗУ получают перебором значений каждого воздействия хi из возрастающей последовательности фиксированных значений
комбинации значений стимулов в ЗУ получают перебором значений каждого воздействия хi из возрастающей последовательности фиксированных значений 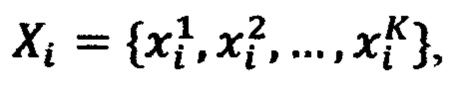 где K - количество фиксированных значений стимулов xi, из соседних значений последовательности Xi в ЗУ образуют K-1 интервалов по каждому стимулу, перебором интервалов по всем переменным x1, х2, …, xN образуют (K-1)N подобластей Ω* в области Ω определения реакции НП F(x1, x2, …, xN), на N входов НП подают стимулы x1*, х2*, …, xN*, определяют принадлежность поданных сигналов некоторой подобласти Ω*, ограниченной интервалами x1min≤x1*<x1max, x2min≤x2*<x2max, …, xNmin≤xN*<xNmax, где x1min, x1max, x2min, x2max, …, xNmin, xNmax - ближайшие значения стимулов из последовательностей Xi, i изменяется от 1 до N, в интервале (х1min, x1max) вычисляют 2N-1 интерполирующих значений реакции НП (ИЗРН) F по формуле
где K - количество фиксированных значений стимулов xi, из соседних значений последовательности Xi в ЗУ образуют K-1 интервалов по каждому стимулу, перебором интервалов по всем переменным x1, х2, …, xN образуют (K-1)N подобластей Ω* в области Ω определения реакции НП F(x1, x2, …, xN), на N входов НП подают стимулы x1*, х2*, …, xN*, определяют принадлежность поданных сигналов некоторой подобласти Ω*, ограниченной интервалами x1min≤x1*<x1max, x2min≤x2*<x2max, …, xNmin≤xN*<xNmax, где x1min, x1max, x2min, x2max, …, xNmin, xNmax - ближайшие значения стимулов из последовательностей Xi, i изменяется от 1 до N, в интервале (х1min, x1max) вычисляют 2N-1 интерполирующих значений реакции НП (ИЗРН) F по формуле
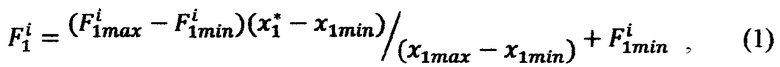
где i - номер промежуточного ИЗРН F на первом шаге вычисления, 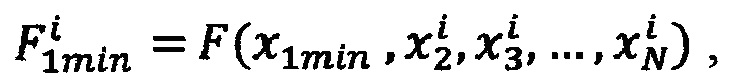
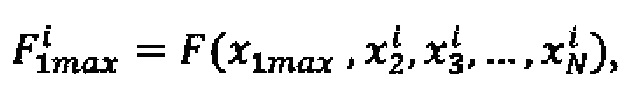
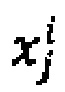 - крайние значения стимулов, ограничивающие выбранную подобласть Ω* в N-мерной области определения реакции НП,
- крайние значения стимулов, ограничивающие выбранную подобласть Ω* в N-мерной области определения реакции НП,

на j-м шаге в интервале [xjmin, xjmax) вычисляют 2N-j ИЗРН F по формуле
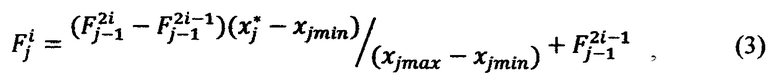
где i - номер промежуточного ИЗРН на j-м шаге (j изменяется от 2 до N), на N-м шаге в интервале [хNmin, хNmax) при j=N по формуле (3) вычисляют искомое значение реакции НП F(x1*, х2*, …, xN*) на сигналы х1*, х2*, …, xN*, для настройки НП в каждую ячейку ЗУ записывают кортежи значений параметров 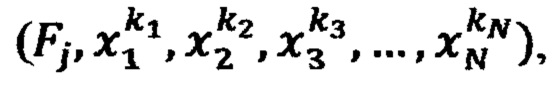 где
где 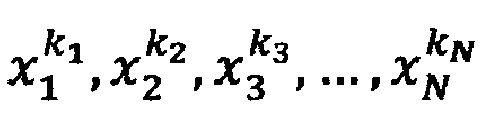 - комбинация заданных значений стимулов, получаемая для каждого стимула xi из возрастающей последовательности
- комбинация заданных значений стимулов, получаемая для каждого стимула xi из возрастающей последовательности 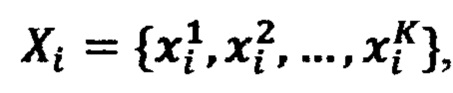 Fj - начальное значение реакции НП при заданных значениях стимулов, формируют обучающие кортежи (d*, х1*, х2*, …, xN*), состоящие из эталонного сигнала d* и соответствующих ему стимулов Х*=(х1*, х2*, …, xN*), на обучающий вход НП поочередно подают эталонные сигналы d1, d2, …, dS, образующие обучающую выборку (эпоху), а на сигнальные входы НП подают соответствующие каждому эталонному сигналу d∈{d1, d2, …dS} стимулы x1 х2, …, xN, эталонные сигналы выбирают так, чтобы в каждой подобласти Ω*∈Ω находился хотя бы один обучающий кортеж, при подаче очередного эталонного сигнала d*∈{d1, d2, …dS} и стимулов Х*=(х1*, х2*, …, xN*) определяют подобласть Ω*, внутри которой находится обучающий кортеж (d*, x1*, x2*, …, xN*), вычисляют реакцию F* НП на стимулы x1*, x2*, …, xN*, вычисляют невязку е*=d*-F*, выполняют пошаговое вычисление невязок в вершинах параллелепипеда, ограничивающего подобласть Ω*, для этого на первом шаге вычисляют невязку в точке (x1*, х2*, …, xNmin) по формуле
Fj - начальное значение реакции НП при заданных значениях стимулов, формируют обучающие кортежи (d*, х1*, х2*, …, xN*), состоящие из эталонного сигнала d* и соответствующих ему стимулов Х*=(х1*, х2*, …, xN*), на обучающий вход НП поочередно подают эталонные сигналы d1, d2, …, dS, образующие обучающую выборку (эпоху), а на сигнальные входы НП подают соответствующие каждому эталонному сигналу d∈{d1, d2, …dS} стимулы x1 х2, …, xN, эталонные сигналы выбирают так, чтобы в каждой подобласти Ω*∈Ω находился хотя бы один обучающий кортеж, при подаче очередного эталонного сигнала d*∈{d1, d2, …dS} и стимулов Х*=(х1*, х2*, …, xN*) определяют подобласть Ω*, внутри которой находится обучающий кортеж (d*, x1*, x2*, …, xN*), вычисляют реакцию F* НП на стимулы x1*, x2*, …, xN*, вычисляют невязку е*=d*-F*, выполняют пошаговое вычисление невязок в вершинах параллелепипеда, ограничивающего подобласть Ω*, для этого на первом шаге вычисляют невязку в точке (x1*, х2*, …, xNmin) по формуле
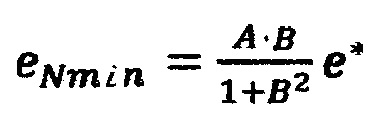
и невязку в точке (х1*, x2*, …, xNmax) по формуле
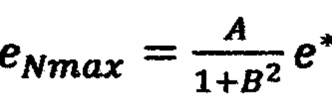 ,
,
где 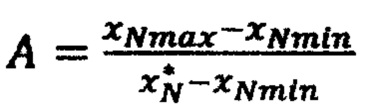 и
и 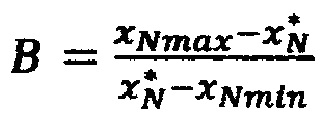 ,
,
на втором шаге вычисляют невязку в точке (х1*, …, xN-1min, xNmin) по формуле
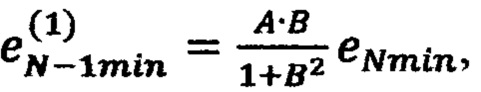
невязку в точке (х1*, …, xN-1max, xNmin) по формуле
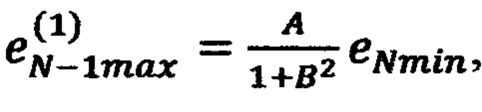
невязку в точке (х1*, …, xN-1min, xNmax) по формуле
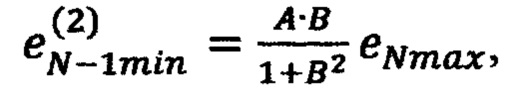
невязку в точке (x1*, …, xN-1max, xNmax) по формуле
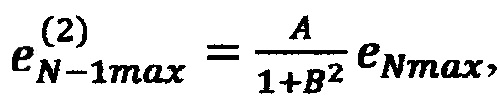
где 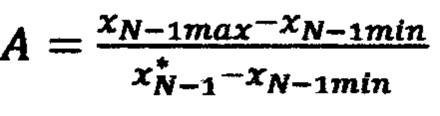 и
и 
на третьем шаге вычисляют невязку в точке (х1*, …, xN-2min, xN-1min, xNmin) по формуле
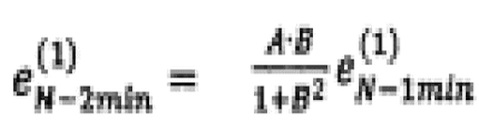 ,
,
невязку в точке (х1*, …, xN-2max, хN-1min, xNmin) по формуле

невязку в точке (х1*, …, xN-2min, xN-1max, xNmin) по формуле
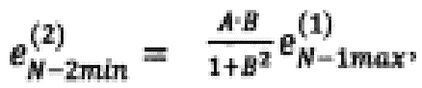
невязку в точке (x1*, xN-2max, xN-1max, xNmin) по формуле
 ,
,
невязку в точке (х1*, …, xN-2min, xN-1min, xNmax) по формуле
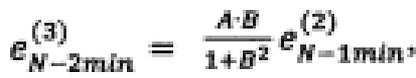
невязку в точкe (x1*, …, xN-2max, xN-1min, xNmax) по формуле
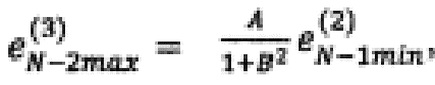
нeвязку в точке (х1*, …, xN-2min, xN-1max, xNmax) по формуле
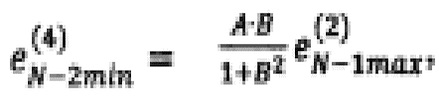
нeвязку в точке (x1*, …, xN-2max, xN-1max, xNmax) по формуле
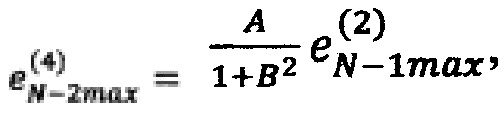
где 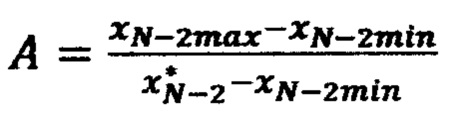 и
и 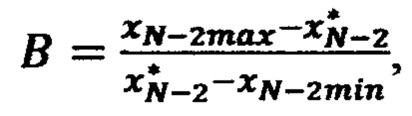
и так далее, продолжая вычисления, на N-м шаге рассчитывают невязку во всех 2N вершинах N-мерного параллелепипеда, ограничивающего подобласть значений Ω*, выполняют корректировку значений реакции F в ЗУ во всех 2N вершинах N-мерного параллелепипеда на величины рассчитанных в них невязок, процедуры расчета невязок и коррекции значений реакции НП F повторяют для всех эталонных обучающих сигналов d1, d2, …, dS до тех пор, пока не будет достигнуто приемлемое отклонение расчетных значений от эталонных в кортежах.
| МОДЕЛЬ НЕЙРОНА, РЕАЛИЗУЮЩАЯ ЛОГИЧЕСКУЮ ФУНКЦИЮ НЕРАВНОЗНАЧНОСТИ | 2003 |
|
RU2269155C2 |
| СПОСОБ МОДЕЛИРОВАНИЯ НЕЙРОНА | 2009 |
|
RU2402813C1 |
| Бесконтактный электромагнитный датчик для измерения крутящего момента, передаваемого вращающимся валом | 1960 |
|
SU148932A1 |
| US 5504839 A, 02.04.1996 | |||
| Гидропривод механизма подачи деревообрабатывающего станка | 1974 |
|
SU526504A1 |
Авторы
Даты
2020-06-25—Публикация
2018-05-18—Подача