Изобретение относится к гравиметрии, в частности к бортовым измерителям вторых производных гравитационного потенциала, например к измерителю тензора вторых производных.
Цель изобретения расширение функциональных возможностей и улучшение технико-эксплуатационных характеристик путем усовершенствования процедуры формирования разностных сигналов, пропорциональных дрейфу нуля и гравитационным помехам во время движения объекта.
Сопоставительный анализ заявляемого решения с прототипом показывает, что заявляемый способ отладки бортового гравитационного градиентометра отличается от известного тем, что вектор измерения в процессе движения бортового носителя формируется на основе определения направления гравитационной вертикали путем интегрирования тензора вторых производных гравитационного потенциала по маршруту движения с использованием в начальный момент времени результатов измерения направления силы притяжения с помощью акселерометров, при этом используются сигналы от пилотажно-навигационного комплекса, пропорциональные
угловым скоростям и угловым ускорениям градиентометра от подвижного объекта для получения невозмущенного угловыми движениями тензора вторых производных гравитационного потенциала. Сущность изобретения заключается в следующем. На бортовом носителе (объекте типа корабль, самолет, наземного или другого транспортного средства) устанавливают на одной гидростабилизированной платформе гравитационный градиентометр (типа ротационных бортовых гравитационных градиентометров или других) и блок трех одноосных акселерометров. Чувствительные оси акселерометров ориентируют параллельно гироплатформенной системе координат. Включают питание и выставляют гиростабилизированную платформу по азимуту и в горизонте по сигналам гироскопов и акселерометров. В процессе движения в бортовой ЦВМ вычисляют
приращение к начальному направлению гравитационной вертикали вследствие перемещения бортового носителя и формируют текущее направление гравитационной вертикали. Причем вертикальное направление в начальный момент времени определяется по сигналам блока акселерометров. При этом из сигналов градиентометрических измерений вычитают помехи, обусловленные угловыми вращениями градиентометров, вызванные траекторными движениями бортового носителя и гироплатформы, на которой установлены блок акселерометров и градиентометр. Помеху от углового ускорения учитывают путем использования операции формирования антисимметричной части измеренного тензоpа. Симметричную составляющую измеренного тензора, связанную наличием помех от угловых скоростей вращения корпуса градиентометра, учитывают путем непосредственного измерения угловых скоростей с помощью
гироскопов пилотажно-навигационного комплекса движущегося объекта, а также путем интегрирования сигналов, соответствующих антисимметричной части измеренного градиентометром тензора. Таким образом получают акселероградиентометрическое направление гравитационной вертикали в текущей точке траектории движения объекта.
Синхронно по времени производят определение градиентометрического направления гравитационной вертикали как собственного вектора тензора вторых производных от геопотенциала для максимального собственного значения.
В результате в заданные моменты времени определяют направление гравитационной вертикали синхронно акселероградиентометрическим и градиентометрическим каналами. Затем сравнивают между собой сигналы, пропорциональные измеренным направлениям гравитационной вертикали по двум каналам. Разность этих сигналов запоминают в ЦВМ в виде вектора измерений направлений гравитационной вертикали, который обрабатывают в ЦВМ с учетом времени измерений и углов поворота гиростабилизированной платформы и бортового носителя. Определяют в конце каждой операции и всех процедуры отладки бортового гравитационного градиентометра поправки, пропорциональные сигналам компенсации за влияние дрейфа нуля, гравитационных помех и систематических дестабилизирующих факторов, по всем шести каналам выходного полезного сигнала.
При этом физической основой заявленного способа отладки градиентометра является использование принципиальных и структурных отличий методических и инструментальных погрешностей измерения направления гравитационной вертикали по синхронным во времени сигналам, формируемым акселероградиентометрическим и градиентометрическим каналами.
Определение направления гравитационной вертикали в акселероградиентометрическом канале осуществляется следующим образом. Известно, что вектор гравитационного ускорения при перемещении из точки rо в точку r вычисляется по формуле
g(r)=go +  T(r)dr, (1)
T(r)dr, (1)
Здесь go вектор гравитационного ускорения в начальной точке. Сигналы, содержащие информацию о векторе gо, получаются от тройки взаимно ортогональных акселерометров. Тензор вторых производных Т(r) формируется в процессе движения бортового носителя из точки rо в точку r с помощью гравитационного градиентометра любой конструктивной формы. Отсюда направление gо гравитационной вертикали определяется как
gо= g/  g
g 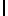 , (2) где
, (2) где  g
g 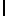 модуль вектора гравитационного ускорения.
модуль вектора гравитационного ускорения.
Из работы следует, что результаты градиентометрических измерений Λ содержит следующую информацию:
Λ= T+Ω( )+Ω2(ω) (3) где Т тензоp вторых производных гравитационного потенциала;
)+Ω2(ω) (3) где Т тензоp вторых производных гравитационного потенциала;
Ω( ) антисимметричный тензор, составленный из компонент абсолютных условных ускорений корпуса гравитационного градиентометра, имеющий следующую структуру
) антисимметричный тензор, составленный из компонент абсолютных условных ускорений корпуса гравитационного градиентометра, имеющий следующую структуру
Ω( )
)  -
-

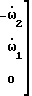
Ω ( ω) антисимметричный тензор, составленный из компонент абсолютных угловых скоростей вращения корпуса гравитационного градиентометра
Ω(ω)  -
-


Поскольку в выражении (3) Ω( ) антисимметричный тензор, а Т и Ω2 ( ω) симметричные тензоры, то, представляя Λ в виде симметричной (Λ (s)) и антисимметричной ( Λ (А)) частей, имеем
) антисимметричный тензор, а Т и Ω2 ( ω) симметричные тензоры, то, представляя Λ в виде симметричной (Λ (s)) и антисимметричной ( Λ (А)) частей, имеем
Λ(A) (Λ-ΛТ)=Ω(
(Λ-ΛТ)=Ω( )
)
Λ(S) (Λ+ΛТ)=T+Ω2(ω) где ΛТ результат транспортирования тензора Λ. Антисимметричная часть Λ(А) содержит только информацию о ω и ее можно проинтегрировать для определения ω. Симметричная часть Λ(S) содержит тензор вторых производных от гравитационного потенциала и центробежную составляющую Ω2, которую можно определить на основе интегрирования результатов определения антисимметричной части Λ(А), а также с использованием непосредственных измерений угловой скорости вращения с помощью гироскопов пилотажно-навигационного комплекса, астрометрическими и другими средствами.
(Λ+ΛТ)=T+Ω2(ω) где ΛТ результат транспортирования тензора Λ. Антисимметричная часть Λ(А) содержит только информацию о ω и ее можно проинтегрировать для определения ω. Симметричная часть Λ(S) содержит тензор вторых производных от гравитационного потенциала и центробежную составляющую Ω2, которую можно определить на основе интегрирования результатов определения антисимметричной части Λ(А), а также с использованием непосредственных измерений угловой скорости вращения с помощью гироскопов пилотажно-навигационного комплекса, астрометрическими и другими средствами.
Определение направления гравитационной вертикали gоградиентометрическом канале производится следующим образом, gоопределяется как направление собственного вектора тензора Т вторых производных гравитационного потенциала Земли, соответствующего его максимальному собственному значению
Тgо= λgо, (4) где goTgо=1. Здесь предполагается, что потенциал притяжения Земли, как это принято в теории гравитационного потенциала, удовлетворяет условию регулярности на бесконечности.
Физическая сущность определения gо заключается в следующем. Из анализа сил, действующих на физический маятник, следует, что положением его устойчивого равновесия является положение по вертикали, когда масса маятника находится ниже точки подвеса, поскольку при любых достаточно малых возмущениях возникают гравитационные моменты, стремящиеся вернуть маятник в прежнее состояние по вертикали. Положением неустойчивого равновесия является его положение, когда чувствительная масса располагается на силовой линии выше точки подвеса.
Для гантели положением устойчивого равновесия также является положение по вертикали, поскольку здесь при любых малых возмущениях возникают гравитационные моменты, стремящиеся вернуть гантель в прежнее состояние по вертикали. Горизонтальные направления являются положениями неустойчивого равновесия, так как любое малое возмущение приводит к возникновению такого гравитационного момента, который будет удалять гантель от горизонтальной плоскости.
Получим уравнение для определения положения устойчивого равновесия гантели в поле гравитационных сил. Как следует из проведенного анализа, это положение совпадает с касательной к силовой линии. В этом положении гравитационный момент М, действующий на гантель, равен нулю. Поэтому необходимое условие равновесия математически представляется в виде
М=2 ρ ˙ Δ g, (5)
Здесь ρ радиус-вектор одной из масс относительно центра масс гантели;
Δ g вектор соответствующего приращения силы притяжения. Имеют место условия
ρт ρconst, выражающее постоянство плеча гантели, и
Δ g=T ρ ≠ 0, характеризующее невырожденность гравитационного поля Земли (для потенциала, регулярного на бесконечности это всегда имеет место). Из выражения (5) с учетом выше приведенных условий следует, что
Δ g= λ ρ, где λ коэффициент пропорциональности. Таким образом, приходим к собственной задаче для определения направления гравитационной вертикали
Tgo= λgо, где gоТgо=1.
Физический смысл собственного значения λ, соответствующего собственному вектору и направлении вертикали заключается в следующем. Вычислим производную от модуля силы напряжения I g I по вектору r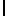 g
g 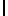 2=gТg, поэтому
2=gТg, поэтому goT
goT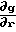
Здесь правую часть преобразуем с помощью (4)
goТ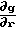
 g
g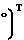 = (Tg°)Т=λg°Т и отсюда находим
= (Tg°)Т=λg°Т и отсюда находим λg°Т. (6)
λg°Т. (6)
Из выражения (6) имеем
λ 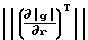
 т.е. собственное число, соответствующее направлению гравитационной вертикали, характеризует максимальную скорость изменения модуля силы притяжения в пространстве, например, для Земли равно 3080Е. В соответствии с данными градиентометрических измерений аномальные значения вторых производных не превосходят нескольких десятков этвеш. Поэтому другие два собственные значения равны приблизительно 1500 Е. При этом целесообразно сделать следующее замечение. Из полученных результатов видно, что от гравитационного потенциала Земли как функции координаты исследуемой точки требуется существование ненулевого тензора вторых производных. В случае нарушения этого маятниковая вертикаль не будет совпадать с гантельной вертикалью.
т.е. собственное число, соответствующее направлению гравитационной вертикали, характеризует максимальную скорость изменения модуля силы притяжения в пространстве, например, для Земли равно 3080Е. В соответствии с данными градиентометрических измерений аномальные значения вторых производных не превосходят нескольких десятков этвеш. Поэтому другие два собственные значения равны приблизительно 1500 Е. При этом целесообразно сделать следующее замечение. Из полученных результатов видно, что от гравитационного потенциала Земли как функции координаты исследуемой точки требуется существование ненулевого тензора вторых производных. В случае нарушения этого маятниковая вертикаль не будет совпадать с гантельной вертикалью.
Действительно, рассмотренная выше физическая картина равновесия гантели либо в однородном поле гравитационных сил, либо в поле, имеющем однородную составляющую, не является справедливой. Это обусловлено тем, что гантель в принципе не реагирует на однородное поле (или на однородную часть поля). Но в соответствии с теорией ньютоновского гравитационного потенциала однородность поля (или его составляющей) в какой-то области пространства приводит к однородности поля во всем пространстве, не занятом притягивающими массами, т. е. к нарушению требования регулярности гравитационного потенциала Земли, как это принято, на бесконечности.
Точность определения направления гравитационной вертикали, обусловленная погрешностями используемых акселерометров и градиентометров, может быть получена из следующих выражений, получающихся варьированием (1), (2) и (4), полагая для определенности, что перемещение бортового носителя происходит по прямой линии, и элементы тензора при этом можно считать постоянными. Отсюда для горизонтальной составляющей гравитационного ускорения имеем
g1=g10+T11х1, следовательно,
Δ g1= Δ g10+ Δ T11x1+T11 Δ x1 (7)
Результаты расчетов по формуле (7) представлены в таблице. Из таблицы видно, что ошибка определения текущего направления гравитационной вертикали в процессе движения бортового носителя определяется величиной погрешности градиентометра (методической и инструментальной) и величиной приращения пространственных координат носителя. Например, при приращениях координат до 5 км, можно формировать направление гравитационной вертикали с точностью на уровне ≈5 угл.с даже при использовании градиентометров с ошибками до 50 Е. Это позволяет использовать акселероградиентометрический метод для формирования эталонного направления гравитационной вертикали.
В соответствии с выражением (3) для результатов непосредственных градиентометрических измерений следует, что поскольку симметричная часть измеренного тензора содержит только центробежную составляющую, то погрешность измерений в 1Е соответствует ошибке определения угловой скорости величиной ≈6  . Учитывая, что точность применяемых гироскопов характеризуется значениями уходов в диапазоне (1,2-0,34) ˙ 10-2
. Учитывая, что точность применяемых гироскопов характеризуется значениями уходов в диапазоне (1,2-0,34) ˙ 10-2 , то соответствующая погрешность формирования тензора вторых производных от геопотенциала составит (0,2-0,06) ˙ 10-2Е, т.е. является малой величиной.
, то соответствующая погрешность формирования тензора вторых производных от геопотенциала составит (0,2-0,06) ˙ 10-2Е, т.е. является малой величиной.
Точность определения направления гравитационной вертикали в начальной точке можно получить из следующего выражения
δ galo= ε /  g
g  (i=1, 2) (8) где δ gaiо погрешность определения направления гравитационной вертикали по сигналам от горизонтальных акселерометров;
(i=1, 2) (8) где δ gaiо погрешность определения направления гравитационной вертикали по сигналам от горизонтальных акселерометров; g
g 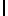 модуль ускорения силы тяжести. Полагая в (8) εi равным (2-20)10-6 I g I или 2-20 мТал, получим точность определения направления гравитационной вертикали
модуль ускорения силы тяжести. Полагая в (8) εi равным (2-20)10-6 I g I или 2-20 мТал, получим точность определения направления гравитационной вертикали
δg 0,42-4,2 угл.с.
0,42-4,2 угл.с.
При этом погрешность определения направления гравитационной вертикали в начальной точке с помощью акселерометров, обусловленная влиянием масс бортового носителя массой в десятки и сотни тонн, не превышает нескольких сотых угловой секунды.
Следует отметить, что влияние гравитационных помех от масс бортового носителя и их перераспределения может достигать 30-50 этвеш. Отсюда в соответствии с результатами расчетов по формуле (8) и табл. 1 для Δ Т11=50 Е и Δ Х1= 100 м максимальная суммарная ошибка определения направления гравитационной вертикали акселероградиентометрическим методом для приращений координат по 5 км составит =6,14-
=6,14- =7,42 угл.с.
=7,42 угл.с.
Точность определения направления гравитационной вертикали градиентометрическим методом можно получить, варьируя выражение (4) в следующем виде
δ Тgo+T δ go= λ δ go+ λ δ go, (9) где δ Т, δ go, δ λ вариации параметров формулы (4)
δ goTgo= 0, (10) где δ goT матрица, транспортированная к матрице-столбцу δ gо.
Умножая выражение (9) на gоT, получим
goT δ Tgo+goT δ go=goT δ λ go+ goT δ λ go,
(11) где goTgo=1 и gоТ δ gо=0
Второй член формулы (11), поскольку он является скалярной величиной, преобразуется к виду
goTT δ go=(goT δ go)T= δ goTTgo= δ goT λgo=0.
Таким образом, приходим к следующей системе уравнений для определения вариаций δ gо направления гравитационной вертикали при использовании градиентометрического метода
δ λgо=gоT δ Tgo
(δ T-E δ λ)go=-(T- λ E) δ go
δ λgoTgo=0, (12) где Е единичная матрица размером (3х3).
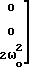
Приведенные соотношения (12) справедливы в любой системе координат. В системе координат ОХ1Х2Х3, где ОХ3 направлена по местной гравитационной вертикали имеют место следующие соотношения
g°
 , δT
, δT 
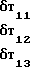


T 
 -
-
 где
где  g
g 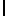 модуль ускорения силы тяжести;
модуль ускорения силы тяжести;
ωo частота Шулера;
частота Шулера; r
r 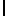 модуль радиуса-вектора от центра масс Земли до исследуемой точки пространства.
модуль радиуса-вектора от центра масс Земли до исследуемой точки пространства.
Согласно уравнениям (12) в принятой системе координат ОХ1Х2Х3получим
δg , δg
, δg (13)
(13)
Принимая в выражении (13) ошибку измерения градиентометром составляющих тензора вторых производных δ Т13 и δ Т23, например, равной 1 этвеш и 3 ωо2= 4500 этвеш, получим точность определения направления вертикали градиентометрическим методом равной
δg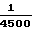 45,8 угл.с.
45,8 угл.с.
При этом погрешность определения направления гравитационной вертикали в градиентометрическом канале, обусловленная методическими погрешностями из-за влияния гравитационных помех от масс бортового носителя на уровне 50 этвеш может достигать примерно 38 угл.мин. Эта погрешность определения направления гравитационной вертикали, достигающая величины 38 угл.мин, градиентометрическим методом значительно превосходит максимальную погрешность формирования этого направления, равную ≈7,4 угл. с акселероградиентометрическим методом.
В заявленном способе отладки бортового гравитационного градиентометра используются вышеуказанные отличия по точности и чувствительности к гравитационным помехам определений акселероградиентометрических и градиентометрических направлений гравитационной вертикали. Поэтому вектор измерений формируется в виде разности направлений гравитационной вертикали (акселероградиентометрической и градиентометрической), которая не зависит от характеристик аномального гравитационного поля Земли, поскольку при этом вычитается их общая часть. Действительно, согласно выражениям (7) и (13), а также результатам расчетов в таблице имеем
Zi1= δga Tio δgTio, (14) где l=1,2;
δgaTiо ошибка определения направления гравитационной вертикали акселероградиентометрическим методом;
δ goTi= δТ3/(3 ωo2) ошибка определения направления гравитационной вертикали градиентометрическим методом. Учитывая в формуле (14), что члены δ gаТio по модулю малы (соответствующая погрешность определения величины δ Тi3 акселероградиентометрическим методом для акселерометров точностью 20х10-6 g, ошибок градиентометров до 50 этвеш, погрешностей формирования координат местоположения до 100 м, приращений координат до 5 км составит ≈0,16 этвеш), и используя нормировку, сформируем сигнал о составляющих вектора измерения в следующем виде:
Zi= δTi3 (15) где Zi=3 ωо2Z
Здесь необходимо отметить следующее. Решение задачи инерциальной навигации сводится к анализу движения некоторой материальной точки (например, чувствительной массы пространственного акселерометра или приведенной точки в случае использования трех ортогональных одноосных акселерометров) единичной массы под действием известных сил. С одной стороны в качестве такой силы выступает реакция на эту точку со стороны некоторой пружины
(механической, электрической, магнитной и т.д. в соответствии с конструктивными особенностями акселерометра). Эта реакция измеряется во время движения объекта. В качестве другой силы выступает гравитационная сила притяжения g, традиционно определяемая для указанной точки в бортовом вычислителе инерциальной навигационной системы при использовании математической модели гравитационного поля Земли.
Для инерциальной системы с бортовым гравитационным градиентометром в процессе решения навигационной задачи необходимо для указанной точки (чувствительной массы пространственного акселерометра) сформировать тензор вторых производных гравитационного потенциала Земли и на его основе вычислить вектор гравитационной силы притяжения в этой точке.
В общем случае сформированный градиентометром тензор является суммой следующих тензоров: тензора вторых производных гравитационного потенциала Земли, тензора вторых производных собственного гравитационного поля от масс бортового носителя, приведенного тензора инструментальных погрешностей градиентометра, тензора, обусловленного угловыми скоростями вращения градиентометра, и, наконец, тензора, связанного с ускоренным угловым движением градиентометра. Перечисленные тензоры нужно определить для указанной точки, например чувствительной массы пространственного акселерометра, с целью последующего удаления помех из сигналов измерений. При этом для отладки градиентометра используются структурные и спектральные отличия поведения различных составляющих ошибок измеренного
градиентометром тензора. Выше было показано, как учитываются составляющие, связанные с вращательными движениями (угловыми скоростями вращения и угловыми ускорениями). Для учета влияния методических и инструментальных погрешностей используется тот факт, что компоненты вектора измерения Zi для i= 1, 2 (см. выражение) (15)) будут по разному изменяться в зависимости от изменения углового положения бортового носителя относительно фиксированной в пространстве платформы с градиентометром и акселерометрами, а также в зависимости от разворотов платформы относительно вертикального направления для фиксированного углового положения бортового носителя.
Составляющие помех в полезный сигнал, обусловленные угловой скоростью вращения и угловым ускорением, не зависят от месторасположения рассматриваемой точки и учет их был рассмотрен выше.
Некоторая неопределенность знания положения чувствительной массы пространственного акселерометра при удалении методической и инструментальной составляющих помех в заявленном способе отладки компенсируются тем, что корректирующие измерения выполняются непосредственно в этой же самой точке с помощью акселерометра (или блока акселерометров).
С другой стороны неопределенность вследствие использования измерителей, находящихся на некотором расстоянии друг от друга, обуславливает дополнительную методическую погрешность формирования сигналов измерений двух гравитационных вертикалей вертикали, определяемой с помощью акселерометров, и вертикали, определяемой с помощью градиентометра. Учитывая, что изменение вертикали вследствие изменения гравитационного поля Земли для перемещений даже величиной 1 м равно сотым долям угловой секунды, то соответствующими ошибками из-за этого фактора в результатах наблюдений Zi (i=1, 2) можно также пренебречь. (угловыми скоростями вращения и угловыми ускорениями). Для учета влияния методических и инструментальных погрешностей используется тот факт, что компоненты вектора измерения Zi для i=1, 2 (см. выражение) (15)) будут по разному изменяться в зависимости от изменения углового положения бортового носителя относительно фиксированной в пространстве платформы с градиентометром и акселерометрами, а также в зависимости от разворотов платформы относительно вертикального направления для фиксированного углового положения бортового носителя.
Составляющие помех в полезный сигнал, обусловленные угловой скоростью вращения и угловым ускорением, не зависят от месторасположения рассматриваемой точки и учет их был рассмотрен выше.
Некоторая неопределенность знания положения чувствительной массы пространственного акселерометра при удалении методической и инструментальной составляющих помех в заявленном способе отладки компенсируются тем, что корректирующие измерения выполняются непосредственно в этой же самой точке с помощью акселерометра (или блока акселерометров).
С другой стороны неопределенность вследствие использования измерителей, находящихся на некотором расстоянии друг от друга, обуславливает дополнительную методическую погрешность формирования сигналов измерений двух гравитационных вертикалей вертикали, определяемой с помощью акселерометров, и вертикали, определяемой с помощью градиентометра. Учитывая, что изменение вертикали вследствие изменения гравитационного поля Земли для перемещений даже величиной 1 м равно сотым долям угловой секунды, то соответствующими ошибками из-за этого фактора в результатах наблюдений Zi (i=1, 2) можно также пренебречь.
Вектор наблюдений (15) содержит в сигнале Zi (i=1, 2) информацию о случайных и методических ошибках измерений вторых производных гравитационного потенциала. Поэтому сигналы являются функциями переменных, определяющих распределение масс бортового носителя, систематических дестабилизирующих факторов и дрейфов нуля градиентометра. Рассмотрим случай, когда масса бортового носителя постоянна, т. е. когда зафиксирована тем или иным образом конфигурация масс носителя, уровень его топлива и т.д. В этом случае величина гравитационных помех является функцией углов α β γ, определяющих ориентацию гироплатформы с градиентометром и акселерометрами относительно корпуса бортового носителя. Дрейфы нуля градиентометра дают составляющие в сигналы Zi, которые являются линейными функциями времени измерений. Влияние систематических дестабилизирующих факторов определяется в виде разности между сигналами вектора измерений и суммарной поправкой от гравитационных помех и дрейфов нуля градиентометра.
Таким образом, с учетом осреднения во времени результатов измерений (порядка нескольких секунд) для исключения высокочастотных помех формула (15) может быть представлена в следующем виде:
Z=Z(α β γ ) Δ Tм ( α β γ ) + Δ +
+ (t -to)D, (16) где где Z  , Δ
, Δ  , D
, D 
ΔTм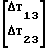 Δ систематические дестабилизирующие факторы.
Δ систематические дестабилизирующие факторы.
D дрейфы нуля градиентометра;
Δ Тм гравитационные помехи от масс бортового носителя.
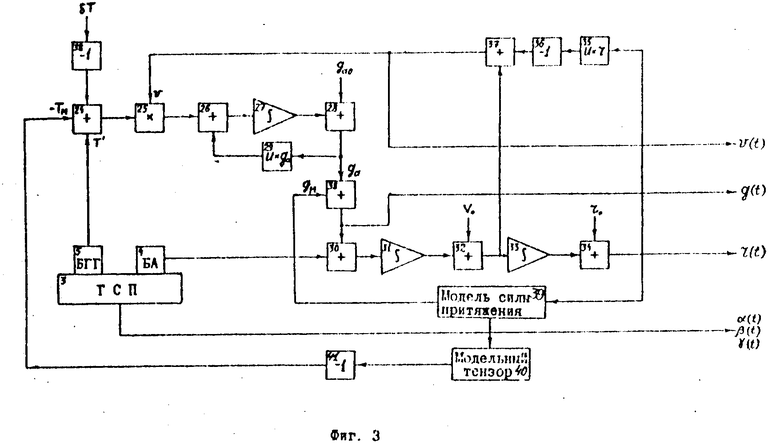
Согласно изобретению, способ отладки бортового гравитационного градиентометра может быть осуществлен с помощью устройства (фиг. 1), содержащего блок измерителей (БИ) 1, включающий бортовой носитель (БН) 2, например, типа автомобильного и железнодорожного транспортного средства и другие, гиростабилизированную платформу (ГСП 3, на которой размещены: блок трех одноосных акселерометров (БА 4 и бортовой гравитационный градиентометр (БГГ) 5, измеряющий тензор вторых производных гравитационного потенциала, вычислитель пилотажно-навигационного комплекса (ВПНК) 6, выдающий текущие значения навигационных параметров бортового носителя (линейную скорость v и координаты местоположения r) и его кинематические параметры (углы ориентации α (t), β (t) и γ (t) носителя относительно системы координат ГСП).
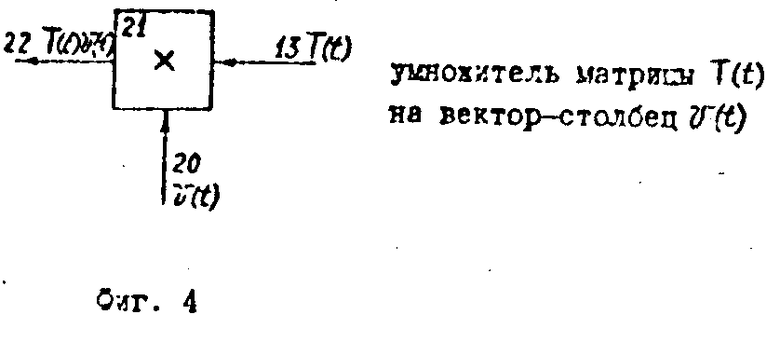
Блок измерителей 1 связан дуплексной связью с блоком формирования измерений (БФИ) 7, который содержит блок управления (БУ) 8, связанный с таймером 9, потребителем выходного полезного сигнала Твых.п/с) 10 градиентометра, например, типа инерциальной геодезической системы и другие, а также с (ЦВМ) 11, которая включает: блок обработки сигналов акселерометров (БОСА) 12, блок обработки сигналов гравитационного градиентометра (БОСГ) 13, блок нормировки (БНР1) 14, блок определения собственного вектора (БОСВ) 15 тензора вторых производных гравитационного потенциала, инвертор 16, сумматор 17, умножитель 18, аналого-цифровой индикатор (АЦИ) 19 выходного полезного сигнала градиентометра и запоминающее устройство (ЗУ) 20 цифровой вычислительной машины, дополнительный умножитель (ДУ) 21, дополнительный интегратор (ДИ) 22 и дополнительный сумматор (ДС) 23.
При этом блок управления 8 связан первым выходом с первым входом блока обработки сигналов акселерометров 12, вторым выходом с первым входом блока обработки сигналов градиентометра 13, третьим входом с первым входом потребителя 10, первым входом с выходом таймера 9, вторым входом мультиплексно связан с четвертым выходом запоминающего устройства 20, третьим входом мультиплексно связан с выходом вычислителя ПНК 6 и четвертым входом мультиплексно связан с выходом ГСП 3, БА 4 и БГГ 5.
Первый выход запоминающего устройства 20 связан с вторым входом БОСА 12, второй выход запоминающего устройства 20 связан с входом сумматора 23, третий выход ЗУ 20 связан с входом умножителя 18, четвертый выход ЗУ 20 с первым входом БОСВ 15, пятый выход ЗУ 20 с вторым входом потребителя 10, шестой выход ЗУ 20 с вторым входом БОСТ 13, седьмой выход ЗУ 20 с входом умножителя 21, первый вход ЗУ 20 связан с выходом БОСА 12, второй вход с выходом БНР1 14, третий вход с выходом АЦИ 19, четвертый вход мультиплексно связан с БУ 8.
Выход блока 13 последовательно связан через блоки 15, 17, 18, 19 с третьим входом ЗУ 20. Кроме того, выход блока 13 последовательно связан через блоки 21, 22, 23, 14, 16, 17, 18, 19 с третьим входом ЗУ 20.
На фиг. 2 показана функциональная схема блока вычитателя ПНК, например, типа [8, 15] который реализует, в частности, следующий порядок получения сигналов, пропорциональных путевой линейной скорости бортового носителя v(t), текущее значение ускорения силы тяжести g(t), пространственные координаты r(t), а также углы ориентации бортового носителя относительно системы координат ГСП α (t), β (t) и γ (t): =v;
=v; =n+g;
=n+g;
g=Tv+u·g, (17) где v=U-u ˙ r;
n кажущееся ускорение, которое измеряется блоком акселерометров;
u вектор угловой скорости вращения Земли, значение которого записано в ЗУ 20, в котором также записаны начальные значения Vо, gо, rо.
Работает вычислитель ПНК следующим образом.
Сигналы БГГ 5 поступают на сумматор 24, где измеренный тензор (Т') вторых производных гравитационного потенциала корректируется по 6 каналам за влияние дрейфа нуля, гравитационных помех и систематических факторов по сигналам, пропорциональным этим поправкам, поступающих от ЗУ 20 через инвертор 38. Далее сигналы, пропорциональные измеренному тензору (Т) вторых производных гравитационного потенциала, поступают на умножитель 25, на второй вход которого поступают сигналы, пропорциональные линейной скорости v(t) носителя относительно Земли, которые получают путем интегрирования показателей БА 4 в интеграторе 31 с учетом значения ускорения силы тяжести (g) в сумматоре 30 и начального значения линейной скорости (Uo) в сумматоре 28. Сигналы, пропорциональные произведению Тv с умножителя 25, поступают на сумматор 26, на второй вход которого поступают сигналы от умножителя 29, осуществляющего векторное умножение вектора угловой скорости вращения Земли (u) на вектор g, который поступает от сумматора 28, на первый вход которого подается сигнал от ЗУ 20 с параметрами, пропорциональными начальному значению gо, а на второй вход сигналы от интегратора 27, осуществляющего интегрирование сигналов, поступающих с сумматора 26. Сигналы от сумматора 32 поступают последовательно на интегратор 33 и сумматор 34, на вход которого от ЗУ 20 поступают начальные значения координат носителя (ro). С выхода сумматора 34 сигналы последовательно проходят через блоки 35, 36 и 37, с помощью которых формируются сигналы, пропорциональные линейной скорости относительно Земли. На инвертор 36 поступают сигналы от умножителя 35, осуществляющего векторное умножение вектора угловой скорости вращения Земли (u) на вектор r, который поступает от сумматора 34. В сумматоре 37 сигнал с инвертора 36 складывается с сигналом, пропорциональным абсолютной скорости движения, поступающим с сумматора 32. С выхода сумматора 37 сигнал подается на вход умножителя 25.
Таким образом, на выходе вычислителя ПНК получают сигналы, пропорциональные v(t), g(t), r(t), а также углы ориентации БН 2 относительно системы координат ГСП 3 α (t), β (t) и γ (t).
На фиг. 3 показана функциональная схема блока вычислителя ПНК, который реализует модифицированный алгоритм получения текущих навигационных и кинематических параметров БН: =V
=V =n+gм+g (18)
=n+gм+g (18)
g=Tav+u ˙ g где v=U-u ˙ r;
Та= Т-Тм аномальное значение тензора вторых производных гравитационного потенциала, как формируемая в реальном масштабе времени разность Т (измеренное значение) и Тм (модельное значение, записанное в виде математической модели гравитационного поля Земли в ЗУ 20);
ga= g-gм аномальное значение ускорения силы тяжести, как разность, вычисляемая в реальном масштабе времени, между g, сформированным на основе измерений, и gм, записанным в виде математической модели гравитационного поля Земли в ЗУ 20);
ga= g-gм аномальное значение ускорения силы тяжести, как разность, вычисляемая в реальном масштабе времени, между g, сформированным на основе измерений, и gм, записанным в виде математической модели ГПЗ в ЗУ 20, в котором записаны также начальные значения Uо, gao, ro.
Поскольку в соответствии с формулой (13) в знаменателе стоит величина (3 ˙ ωо2), равная сумме модулей горизонтального и вертикального градиентов, то при использовании данной схемы вычислителя ПНК, с бортовыми моделями геопотенциала, формируется тензор аномального поля и поэтому указанная сумма равна модулю аномальной горизонтальной второй производной плюс модуль аномальной вертикальной производной. При этом отношение суммы модулей для аномалий к сумме модулей для абсолютных значений по порядку величины равно 100Е:4500=1: 45, т.е. величина ошибки определения соответствующего направления возрастает не менее чем на порядок. Поэтому данная схема вычислителя ПНК является предпочтительной для обнаружения ошибок бортовых гравитационных градиентометров в предлагаемой процедуре отладки. Кроме того, схема построения вычислителя ПНК является более удобной и рациональной с точки зрения ее аппаратурной реализации, поскольку БГГ измеряет не абсолютную, а только аномальную часть поля, что приводит к значительному сужению динамического диапазона измерений и улучшению условий функционирования градиентометра.
Работает вычислитель ПНК с бортовыми моделями геопотенциала следующим образом.
В отличие от традиционной схемы вычислителя ПНК (фиг. 2) в данном вычислителе дополнительно введены три блока блок математической модели силы тяжести 39, входящей составной частью ЗУ 20, блок математической модели тензора вторых производных гравитационного потенциала 40, входящий составной частью ЗУ 20, и блок инвертора 41, причем блок 39 связан с выходом блока ЗУ 20 и со вторым входом блока 38, а блок 40 последовательно связан с блоком 39, 41 и 42.
Таким образом, в отличие от традиционной схемы вычислителя РНК (фиг. 2) в блоке 24 реализуется алгоритм получения Та=Т-Тм и в блоке 38 алгоритм ga= g-gм, что, как указывалось выше, приводит к существенному выигрышу в точности определения поправок БГГ и к улучшению его динамических и эксплуатационных характеристик.
На фиг. 4, 5, 6 показаны дополнительные функциональные блоки ЦВМ 11 и связи между ними. Блоки дополнительного умножителя 21, дополнительного интегратора 22 и дополнительного сумматора 23 выполнены с использованием известной элементной базы типа БИС серии К 840 и др. Остальные функциональные блоки ЦВМ 11 сохранили свою функциональную структуру как в изобретении прототипе.
Работу устройства (фиг. 1), реализующего заявленный способ отладки бортового гравитационного градиентометра, проиллюстрируем на примере осуществления процедуры отладки, включающей четыре цикла, которые выполняются в блоке формирования измерений 7 по командам блока управления 8 под контролем программируемого таймера 9. 1. Первый цикл процедуры отладки гравитационного градиентометра по определению поправок за влияния дрейфа нуля включает следующие операции: 1.1 операцию горизонтирования и выставки ГСП 3 бортового носителя 2 блока измерений 1, которую осуществляют методом гирокомпасирования с использованием сигналов акселерометров и гироскопов; 1.2 операцию определения блоком обработки сигналов акселерометров 12 начального значения вектора силы притяжения gао и запоминание его в ЗУ 20; 1.3. операцию измерений и запоминания в ЗУ 20 значений начальных углов ориентации αo βo γo БН 2 относительно платформенной системы координат ГСП 3; 1.4. операцию синхронных по времени измерений направлений гравитационной вертикали на момент времени t1 с временем осреднения Тос акселероградиентометрическим и градиентометрическим методом. При этом сигналы от вычислителя ПНК 6 поступают через БУ 8 на ЗУ 20 и дополнительный умножитель 21, где перемножаются с сигналами, пропорциональными тензору вторых производных гравитационного потенциала Т(t), поступающими от БГГ 5 через БУ 8 и БОСГ 13. Затем произведения сигналов Т(t)v(t) поступают на дополнительный интегратор 22 и подаются на сумматор 23, в котором складываются с сигналами, пропорциональными gао, полученными в результате предыдущей процедуры 1.2 по сигналам от БА 4, прошедшими через БУ 8 и БОСА 12 и хранящимися в ЗУ 20. Суммарный сигнал от блока 23 поступает последовательно через блоки 14, 16 на сумматор 17, на второй вход которого подаются сигналы, пропорциональные градиентометрическому направлению вертикали, полученные от БГГ 5 после последовательной обработки в блоках 8, 13 и 15. Выходные сигналы сумматора 17 подаются через блоки 18 и 19 и запоминают в ЗУ 20 в функции времени измерений; 1.5 операцию аналогичную, как и 1.4, выполняют в момент времени t2 с заданным таймером 8 интервалом времени Δ t=t2-t1; 1.6 операцию определения в ЦВМ 11 величины дрейфа градиентометра по двум каналам его полезного сигнала (Т13 и Т23). Результаты определения дрейфов D1 и D2градиентометра фиксируют в ЗУ 20. На этом цикл 1 процедуры отладки БГГ завершают.
2. Второй цикл процедуры отладки гравитационного градиентометра по определению поправок, обусловленных гравитационными помехами от масс бортового носителя включает следующие операции;
2.1. операцию поворота бортового носителя 2 в заданном диапазоне углов относительно ГСП 3 (платформенной системы координат), которую выполняют по командам таймера 9;
2.2 операцию горизонтирования и выставки ГСП 3, которая включает по командам таймера 9 вышеуказанные действия (см. операцию 1.1);
2.3. операцию измерения и запоминания в ЗУ 20 для соответствующего момента времени tj осредненных значений углов αj βj γj (j=3, 4, n, где n ≥ 6) поворота бортового носителя 2 относительно ГСП 3;
2.4. операцию синхронных по времени измерений в блоке акселерометров 4 и блоке градиентометра 5 в момент времени tj с временем осреднения Тос, которая выполняется аналогично операции 1.4.
Операции 2.1-2.4 выполняют для значений j=3, 4, n, где n ≥ 6, 2.5. операцию определения в ЦВМ 11 величин гравитационных помех. Результаты определения поправок Δ Тк фиксируют в ЗУ 20. 2.6. операцию по определению поправок от перераспределения масс бортового носителя, например, вследствие изменения уровня топлива в баках, изменения конфигурации объекта, т.е. обусловленных изменением контролируемых переменных, определяющих состояние масс, в бортовом носителе и их изменчивость (величина уровня жидкости в баках, интервал перемещения массы, угол отклонения штанг с массами и т.д.). При этом осуществляются операции 1-5 цикла 2 по командам таймера 9 для заданных значений контролируемых переменных. В результате получают поправки Δ Тк, k=1, 2, 6 как функции контролируемых переменных и фиксируют значения этих параметров в ЗУ 20. На этом цикл 2 процедуры отладки БГГ заканчивается. 3. Третий цикл процедуры отладки гравитационного градиентометра по определению поправок за влияние систематических дестабилизирующих факторов Δ i(i=1, 2) используют результаты синхронных измерений, проведенных в предыдущих циклах 1 и 2 отладки, в блоке акселерометров 4 и блоке гравитационного градиентометра 5, а также полученные в ЦВМ 11 значения дрейфов и гравитационных помех. Результаты определения поправок Δ i(i=1, 2) фиксируют в ЗУ 20. На этом цикл 3 процедуры БГГ завершается.
В результате выполнения вышеуказанных циклов процедуры отладки получают поправки градиентометрических наблюдений (дрейф и систематический фактор) по двум каналам, соответствующими градиентам Т13и Т23 и одновременно определяют величины гравитационных помех для всех 6 каналов градиентометра 5. 4. Четвертый цикл процедуры отладки гравитационного градиентометра по определению дрейфов и систематических факторов для остальных 4 каналов градиентометра заключается в следующем. Нужно повторить операции 3-6 первого цикла и цикл третий процедуры отладки градиентометра. При этом как в цикле два изменяют углы ориентации ГСП 3 относительно неподвижного БН 2 (т.е. величины, обозначенные в операции 2 цикла 1 через αo βo γo) с установленными на ней блоками акселерометров 4 и градиентометром 5, например, на фиксированную величину в 5-6о или 90о (в зависимости от конструктивного исполнения бортового гравитационного градиентометра). Результаты определения Di и Δ i (i=3, 4, 5, 6) фиксируют в ЗУ 20. На этом цикл 4 процедуры отладки БГГ заканчивается.
В результате выполнения циклов 1-4 процедуры отладки БГГ в ЗУ 20 хранится три основных типа поправок по каждому из шести каналов выходного полезного сигнала гравитационного градиентометра. В рабочем режиме измерений градиентометра 5 из его выходного сигнала на каждому из шести каналов в БУ вычитают сигналы, пропорциональные полученным поправкам, хранящимся в ЗУ 20, и затем подают к потребителю полезного сигнала градиентометра 10, например, инерциальную геодезическую систему и др.
Точность определения поправок в заявленном способе обеспечивается в пределах 0,4-0,8Е. Использование предлагаемого способа для коррекции сигналов современных бортовых гравитационных градиентометров различных конструкций позволило существенно увеличить точность и надежность измерений за час работы в процессе движения бортового носителя за счет компенсации инструментальных и методических погрешностей с уровня в 40-60Е до уровня 0,9-2,2Е, т.е. в 30-40 раз улучшается отношение сигнал/шум.
Использование предлагаемого способа отладки бортового гравитационного градиентометра обеспечивает по сравнению с существующими известными способами отладки следующие преимущества:
осуществлять компенсацию инструментальных и методических погрешностей градиентометра, обусловленных влиянием дрейфа нуля, гравитационными помехами от масс бортового носителя и систематических факторов непосредственно в процессе движения, что в целом приводит к увеличению отношения сигнал/шум в выходном полезном сигнале градиентометра в 30-40 раз. Таким образом увеличивается точность и надежность измерений гравитационного градиентометра при соотношении сигнал/помеха большим и близким к единице;
достигать вследствие высокой точности и помехозащищенности заявленного способа отладки бортовых гравитационных градиентометров значительного увеличения производительности и оперативности проведения гравитационно-градиентной съемки для создания, например, местных геодезических построений, определения текущих значений уклонений отвесной линии, а также для решения геофизических и гидрографических проблем и др.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОТЛАДКИ БОРТОВОГО ГРАВИТАЦИОННОГО ГРАДИЕНТОМЕТРА | 1988 |
|
SU1517582A1 |
| ОБРАБОТКА ДАННЫХ ГРАВИМЕТРИЧЕСКОЙ СЪЕМКИ | 2008 |
|
RU2486549C2 |
| Способ спутниковой гравитационной градиентометрии | 2020 |
|
RU2745364C1 |
| Способ морской гравиметрической съемки и устройство для его осуществления | 2020 |
|
RU2767153C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СТАЦИОНАРНОГО ГЕОМАГНИТНОГО ПОЛЯ ПРИ ПРОВЕДЕНИИ МОРСКОЙ МАГНИТНОЙ СЪЕМКИ | 2010 |
|
RU2433427C1 |
| ГРАВИМЕТРИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ УКЛОНЕНИЯ ОТВЕСНОЙ ЛИНИИ В ОКЕАНЕ НА ПОДВИЖНОМ ОБЪЕКТЕ | 2007 |
|
RU2348009C1 |
| ИЗМЕРИТЕЛЬНЫЙ БЛОК ДЛЯ ГРАВИТАЦИОННОГО ГРАДИЕНТОМЕТРА | 2017 |
|
RU2668954C1 |
| ГРАВИТАЦИОННЫЙ ГРАДИЕНТОМЕТР | 2009 |
|
RU2517954C2 |
| АСТРОНАВИГАЦИОННАЯ СИСТЕМА | 2015 |
|
RU2592715C1 |
| НАВИГАЦИОННЫЙ КОМПЛЕКС ПОДВИЖНОГО ОБЪЕКТА | 2014 |
|
RU2563326C1 |





Использование: гравиметрия, в частности для измерения бортовым измерителем вторых производных гравитационного потенциала. Сущность: усовершенствована процедура измерения шести компонент тензора вторых производных гравитационного потенциала и компенсации в его полезном сигнале методических и инструментальных погрешностей, обусловленных дрейфом нуля, гравитационными помехами от масс бортового носителя и их перераспределения, а также влиянием систематических дестабилизирующих факторов. Во время движения бортового носителя в процессе обработки сигналов, пропорциональных вектору измерений, суммируют сигналы акселерометров с сигналами, пропорциональными значениям интеграла от вторых производных гравитационного потенциала, поступающими с выхода градиентометра, по приращениям пространственных координат бортового носителя для заданного интервала времени интегрирования, подаваемых от вычислителя пилотажно-навигационного комплекса бортового носителя, сигналы которого пропорциональны также текущим значениям навигационных и кинематических параметров бортового носителя. 6 ил. 1 табл.
СПОСОБ ОТЛАДКИ БОРТОВОГО ГРАВИТАЦИОННОГО ГРАДИЕНТОМЕТРА, включающий измерение бортовым гравитационным градиентометром шести независимых компонент тензора вторых производных гравитационного потенциала и компенсацию методических инструментальных погрешностей, обусловленных дрейфом нуля, гравитационными помехами от масс бортового носителя и их перераспределения, а также влиянием систематических дестабилизирующих факторов, путем обработки измерений разности направлений гравитационной вертикали по синхронным по времени сигналам акселерометров и градиентометра, установленных на одной гидростабилизированной платформе при различных ориентациях бортового носителя относительно гидростабилизированной платформы и поворотах на заданные углы гиростабилизированной платформы относительно бортового носителя, отличающийся тем, что, с целью расширения функциональных возможностей, отладка бортового гравитационного градиентометра осуществляется во время движения бортового носителя, а сигналы акселерометров суммируют с сигналами, пропорциональными значениям интеграла от вторых производных гравитационного потенциала, по приращениям пространственных координат бортового носителя для заданного интервала времени интегрирования, определяемым пилотажно навигационным комплексом бортового носителя.
| СПОСОБ ОТЛАДКИ БОРТОВОГО ГРАВИТАЦИОННОГО ГРАДИЕНТОМЕТРА | 1988 |
|
SU1517582A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
Авторы
Даты
1995-09-20—Публикация
1989-12-26—Подача