Изобретение относится к обработке металлов давлением и может быть использовано для построения кривой предельной пластичности при испытаниях металлов на пластичность в центральных заводских лабораториях или лабораториях научно-исследовательских институтов.
Известен способ построения кривой предельной пластичности, включающий изготовление образцов, их испытание на пластичность путем сжатия.
Недостатком известного способа является невысокая точность и достоверность результатов испытаний, проводимых без учета исходной формы образцов, моделирующих различные виды заготовок и схемы деформаций.
Технический результат, получаемый от использования настоящего изобретения, заключается в повышении точности получаемых при испытании на пластичность результатов, необходимых для построения кривой предельной пластичности.
Технический результат достигается тем, что, согласно способу построения кривой предельной пластичности, включающему изготовление образцов, их испытания на пластичность путем сжатия до разрушения, испытанию сжатием или прокаткой подвергают образцы с цилиндрической, выпуклой и вогнутообразной формой боковой поверхности с различной степенью выпуклости и вогнутообразности, при этом напряженно-деформированное состояние определяют на свободной поверхности в горизонтальной плоскости симметрии образцов, а кривую предельной пластичности строят путем определения коэффициентов предложенной ниже функции.
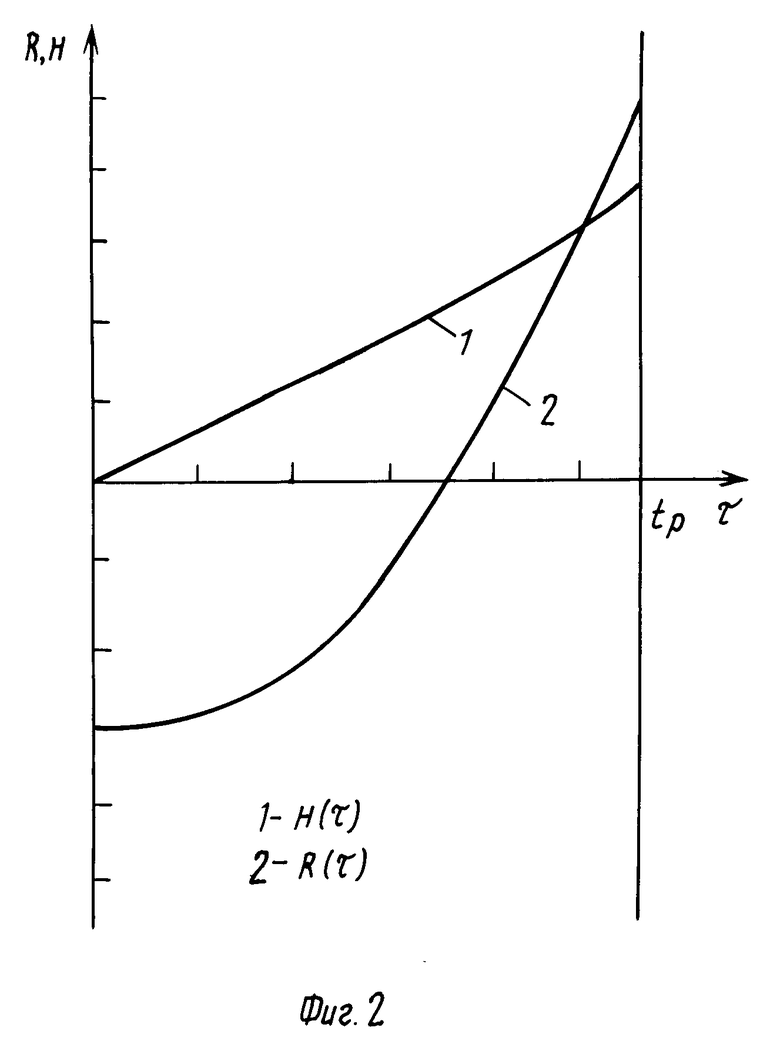
На фиг. 1 показаны исходные образцы, используемые при осадке; на фиг. 2 график изменения интенсивности скорости деформации и коэффициенты жесткости схемы напряженного состояния во времени.
Способ осуществляется следующим образом. Из слитка или заготовки отрезают темплеты необходимых размеров. Из темплетов изготовляют образцы цилиндрической, выпуклой или вогнутообразной формы. При этом выпуклоcть и вогнутообразноcть образцов имеют различную величину. На свободную поверхность в горизонтальной плоскости симметрии осаживаемых образцов наносят две отметки. Таким образом изготовленные образцы осаживают до разрушения на прессе, имеющем необходимую скорость деформирования. В процессе осадки измеряют расстояние между отметками. Для этого возможно использовать тензодатчики, фотокамеру, фотоаппарат или измерения возможно производить, используя инструментальный микроскоп. Обработку полученных данных производят по следующей методике.
В плоскости с нормалью 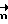 к свободной от нагрузки поверхности осаживаемого цилиндрического, конического и бочкообразного образцов нормальные и касательные напряжения равны нулю. В точке A (см. фиг. 1) вектор
к свободной от нагрузки поверхности осаживаемого цилиндрического, конического и бочкообразного образцов нормальные и касательные напряжения равны нулю. В точке A (см. фиг. 1) вектор 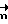 совпадает с направлением оси ρ( ρ,θ,z оси цилиндрической системы координат) и условия на границе в точке A имеют вид
совпадает с направлением оси ρ( ρ,θ,z оси цилиндрической системы координат) и условия на границе в точке A имеют вид
σρ 0; σρθ=σρz 0. (1) Используя физические уравнения связи напряжений и деформаций для деформационной теории или уравнения физической связи напряжений и скоростей деформации теории течения
σm-σ 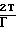
 m, σm- σ
m, σm- σ 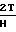 ζ, (2) где m= 1, 2, 3 или m ρ,θ z;
ζ, (2) где m= 1, 2, 3 или m ρ,θ z;
Т интенсивность напряжений сдвига;
Ξ- интенсивность скоростей деформаций сдвига;
Γ интенсивность логарифмической деформации. При известных граничных условиях (1) можно определить напряжения σθ и σz (σρ 0) на свободной от нагрузки поверхности, если известны компоненты логарифмических деформаций 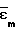 или скоростей деформаций ζm. Главные деформации
или скоростей деформаций ζm. Главные деформации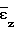 = ln
= ln 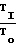
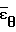 ln
ln 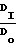
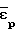 = -(
= -(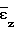 +
+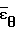 ) (3) определяются с использованием измеренных расстояний между отметками до деформации То и на любой стадии деформирования ТI, а также измерением диаметра образца Do, в меридиальном сечении до деформации и DI в любой I-й момент времени.
) (3) определяются с использованием измеренных расстояний между отметками до деформации То и на любой стадии деформирования ТI, а также измерением диаметра образца Do, в меридиальном сечении до деформации и DI в любой I-й момент времени.
При отсутствии поворотов главных осей относительно одних и тех же материальных волокон скорость деформации в направлении координатных осей определяется формулой
ζm= d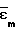 /dτ (4) Время τ и относительное обжатие ε при постоянной скорости деформирования v const связаны соотношениями
/dτ (4) Время τ и относительное обжатие ε при постоянной скорости деформирования v const связаны соотношениями
ε 
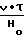 dε
dε 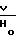 dτ (5) поэтому в дальнейшем скорость деформации ζm
dτ (5) поэтому в дальнейшем скорость деформации ζm
ζm= 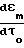
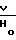
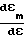 т.е.
т.е.
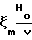 ζm=
ζm= 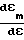
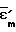 (6) будет определяться с точностью до постоянного множителя v/Ho. Операция дифференцирования, используемая для определения
(6) будет определяться с точностью до постоянного множителя v/Ho. Операция дифференцирования, используемая для определения 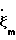 =
= 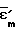 по формулам (6), существенно снижает точность вычисления ζm. Успех решения задачи вычисления
по формулам (6), существенно снижает точность вычисления ζm. Успех решения задачи вычисления 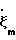 во многом зависит от удачной аппроксимации зависимостей
во многом зависит от удачной аппроксимации зависимостей 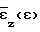 и
и 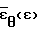 , в результате чего
, в результате чего 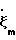 =
= 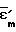 определяются аналитически.
определяются аналитически.
В данном способе процесс деформирования исследуют во времени и функции 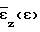 и
и 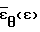 аппроксимируют рядами, сплайнами, полиномами Чебышева или какими-либо другими способами для сглаживания и дифференцирования по времени экспериментально получаемых величин.
аппроксимируют рядами, сплайнами, полиномами Чебышева или какими-либо другими способами для сглаживания и дифференцирования по времени экспериментально получаемых величин.
Наибольшие погрешности определения 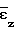 и
и 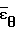 получаются при малых деформациях, в связи с чем при аппроксимации
получаются при малых деформациях, в связи с чем при аппроксимации 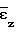 (τ) и
(τ) и 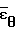 (τ) целесообразно использовать начальные условия при τ 0 для самой функции
(τ) целесообразно использовать начальные условия при τ 0 для самой функции 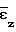 (τ),
(τ), 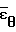 (τ) и ее производных по времени
(τ) и ее производных по времени 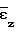 ,
,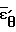 и
и 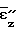 ,
, 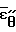 в виде
в виде
ε0; 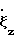 =
= 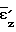 = 1;
= 1; 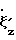 =
= 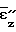 -1;
-1;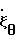 =
= 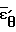 = 0,5;
= 0,5; 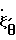 =
= 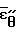 0,5. (7) В условиях (7) было принято, что при τ->0 действие сил трения незначительно и деформация цилиндрического, конического и бочкообразного образца равномерна, в связи с чем из уравнения
0,5. (7) В условиях (7) было принято, что при τ->0 действие сил трения незначительно и деформация цилиндрического, конического и бочкообразного образца равномерна, в связи с чем из уравнения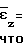
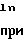 T
T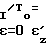 l
l
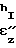 /
/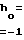 2 ln DI/Do= 2
2 ln DI/Do= 2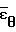 = ln (1-ε) (следует/ Обработку результатов эксперимента проводят на ЭВМ.
= ln (1-ε) (следует/ Обработку результатов эксперимента проводят на ЭВМ.
Кинематические и статистические параметры процесса осадки в окрестности точки А (фиг. 1) определяют по следующим формулам теории течения:
σm-σ 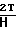 ζm; kζ=
ζm; kζ= 
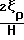
σz= 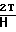 (ζz-ζρ); σθ=
(ζz-ζρ); σθ= 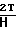 (ζθ-ζρ);
(ζθ-ζρ);
H 2 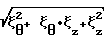 ;
;
Λ ∫ Ηdτ, где Λ степень деформации;
σ- среднее напряжение;
kζ- коэффициент жесткости схемы напряженного состояния. Для построения кривой предельной пластичности воспользовались формулой определения степени использования ресурса
Ψ ∫ 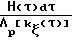 (8) и полученные экспериментальные данные по исследованию напряженно-деформированного состояния на свободной поверхности при осадке (фиг. 2).
(8) и полученные экспериментальные данные по исследованию напряженно-деформированного состояния на свободной поверхности при осадке (фиг. 2).
В формуле (8) Λp [kζ(τ)] является неизвестной функцией, ее предстоит определить по механическим испытаниям, когда H (τ) и k( τ) меняется во времени (фиг. 2), но известна точка разрушения и время разрушения tp.
Возьмем функцию, обратную Λp
Vp=  am·k
am·k
Тогда
Ψ = 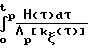
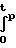 Vp[kζ(τ)]·H(τ)dτ= 1 Пусть
Vp[kζ(τ)]·H(τ)dτ= 1 Пусть
Vp ao + a1 ˙kζ+ a2 ˙kζ2+. + am ˙kζm, тогда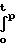 (a0+a1·k
(a0+a1·k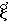 +a2·k
+a2·k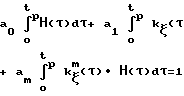 )Η(τ)dτ + a
)Η(τ)dτ + a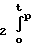 k
k
(9) где n количество испытаний (количество типов осаживаемых образцов), равное количеству членов полинома. Поинтегральные выражения в формуле (9) определяются по экспериментальным данным, численным интегрированием.
Получаем систему: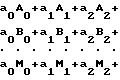
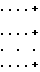
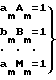


Решением системы линейных уравнений определяем коэффициенты аo, a1, a2, am аппроксимирующего уравнения
Vp am ˙kζm (10) и по соотношению (10) определяется
Λp= f(kζ) 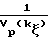 (11) Предложенный способ построения кривой предельной пластичности сопоставляется с известными методами и находится различие кривых Λp f(kζ)
(11) Предложенный способ построения кривой предельной пластичности сопоставляется с известными методами и находится различие кривых Λp f(kζ)
Данный способ можно осуществить и прокаткой. Для этого изготовляются образцы с вогнутообразной, выпуклообразной и цилиндрической формой боковой поверхности, c нанесенной координатной сеткой и прокатываются до разрушения. Методика обработки экспериментальных данных и построения кривой предельной пластичности аналогично как и при осадке.
П р и м е р. Построение кривой предельной пластичности производили на алюминиевых образцах марки АМГ-6 размером ⊘ 50 х 100 мм. Образцы имели различную вогнутость и выпуклость. Вследствие наличия инструментальных, измерительных, случайных и других погрешностей точность определения скоростей деформации во многом зависит от точности проведения измерения D, T, h. В связи с этим при реализации эксперимента для повышения точности измерения исходных данных (D, T, h) в любой момент времени τ=τI использовали инструментальный микроскоп МПБ-2, обеспечивающий точность измерения 0,01 мм, а также увеличивали число измерений параметров на каждом этапе деформирования до четырех. С целью снижения влияния погрешностей на результаты вычислений функцию 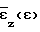 и
и 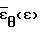 аппроксимировали степенными полиномами
аппроксимировали степенными полиномами 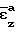 = anεn ,
= anεn , 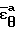 = bnεn. Обработку результатов эксперимента проводили по методике, приведенной выше, на ЭВМ.
= bnεn. Обработку результатов эксперимента проводили по методике, приведенной выше, на ЭВМ.
Для оценки надежности вычислений аппроксимированных значений 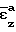 и
и 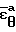 определяли абсолютное отклонение
определяли абсолютное отклонение 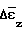 и
и 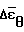 этих величин от средних экспериментальных
этих величин от средних экспериментальных 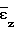 и
и 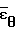 а также их среднеквадратичное отклонение Sz и Sθ от опытных значений. Их максимальные значения следующие:
а также их среднеквадратичное отклонение Sz и Sθ от опытных значений. Их максимальные значения следующие: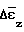 = 0,005;
= 0,005; 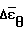 = 0,002; Sz= 0,005; Sθ= 0,002
= 0,002; Sz= 0,005; Sθ= 0,002
Проведение данного эксперимента позволило построить кривую предельной пластичности сплава АМГ-6, которую сопоставляли с известной кривой предельной пластичности сплава АМГ-6. Кривые с инженерной точностью совпали между собой.
Таким образом настоящее изобретение с малыми затратами и достаточной точностью позволяет построить кривую предельной пластичности.
| название | год | авторы | номер документа |
|---|---|---|---|
| ИНСТРУМЕНТ ДЛЯ ПРОТЯЖКИ | 1992 |
|
RU2050217C1 |
| ИНСТРУМЕНТ ДЛЯ КОВКИ | 1992 |
|
RU2050218C1 |
| Слиток | 1990 |
|
SU1724421A1 |
| Инструмент для осадки заготовок | 1991 |
|
SU1780912A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЛАСТИЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ | 2016 |
|
RU2617798C1 |
| Способ изготовления пресс-изделий | 1985 |
|
SU1348048A1 |
| СПОСОБ МНОГООПЕРАЦИОННОЙ ВЫТЯЖКИ КОРОБЧАТОЙ ДЕТАЛИ ИЗ ЛИСТОВОЙ ЗАГОТОВКИ | 2013 |
|
RU2545863C2 |
| УСТРОЙСТВО ДЛЯ КОНТРОЛЯ ДЕФОРМАЦИИ ПОЛИМЕРА ПРИ РАСТЯЖЕНИИ | 1991 |
|
RU2042941C1 |
| СПОСОБ ИСПЫТАНИЯ ЛИСТОВЫХ МАТЕРИАЛОВ НА ДВУХОСНОЕ РАСТЯЖЕНИЕ | 2007 |
|
RU2344407C1 |
| СПОСОБ ПОСТРОЕНИЯ ДИАГРАММЫ ПРЕДЕЛЬНЫХ ДЕФОРМАЦИЙ ЛИСТОВОГО МАТЕРИАЛА | 2015 |
|
RU2591294C1 |
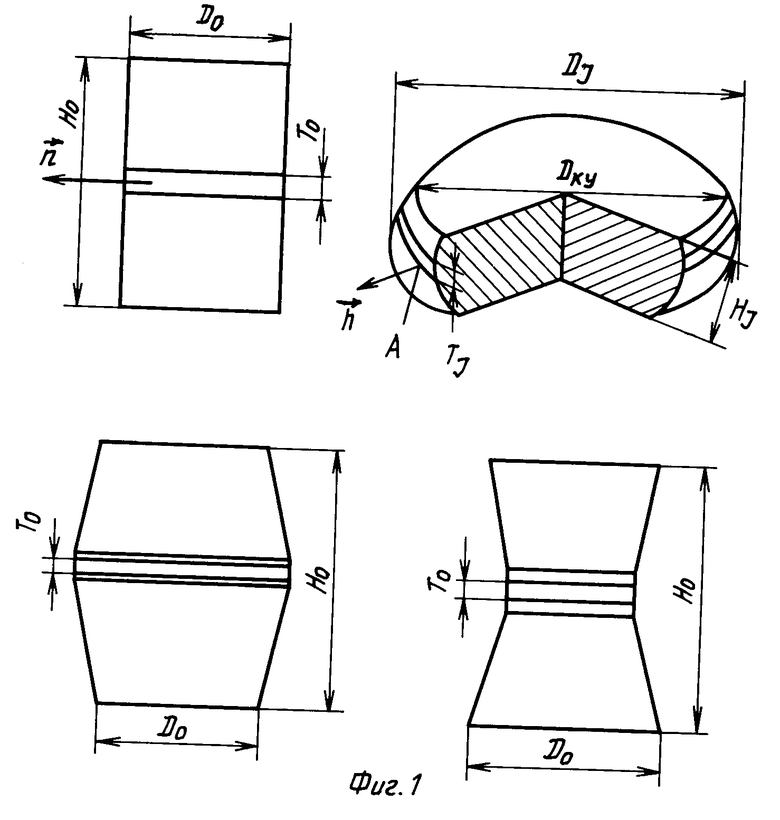
Использование: обработка металлов давлением, в частности испытания материалов на пластичность для построения кривой предельной пластичности. Сущность изобретения: перед испытанием на пластичность изготавливают образцы с вогнутообразной, выпуклой и цилиндрической формой боковой поверхности. Испытание производят путем сжатия или прокатки изготовленных образцов. Напряженно-деформированное состояние определяют на свободной поверхности в горизонтальной плоскости симметрии образцов. Кривую предельной пластичности строят путем определения коэффициентов приведенной функции. 2 ил.
СПОСОБ ПОСТРОЕНИЯ КРИВОЙ ПРЕДЕЛЬНОЙ ПЛАСТИЧНОСТИ, включающий изготовление образцов, их испытание на пластичность путем сжатия до разрушения, отличающийся тем, что для построения кривой предельной пластичности осаживают или прокатывают образцы с цилиндрической, выпуклой и вогнутообразной формой боковой поверхности и с различной степенью выпуклости и вогнутообразности, при этом напряженно-деформированное состояние определяют на свободной поверхности в горизонтальной плоскости симметрии образцов, а кривую предельной пластичности строят путем определения коэффициентов функции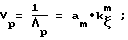
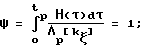
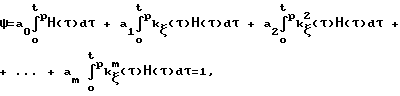
где a0, a1,am коэффициенты уравнения;
Λp предельная степень деформации;
kζ коэффициент жесткости схемы напряженного состояния;
H интенсивность скорости деформации;
t время от начала до конца деформации;
tр время в момент разрушения;
j степень использования ресурса пластичности,
для каждого типа образца или эксперимента.
| Пластичность и разрушение под ред | |||
| В.Л.Колмогорова М.: Металлургия, 1977, с.308-309. |
Авторы
Даты
1995-11-10—Публикация
1992-04-30—Подача