Предлагаемый прибор предназначен для решения системы линейных уравнений со многими неизвестными по методу последовательного приближения, осуществляемому механическими приспособлениями.
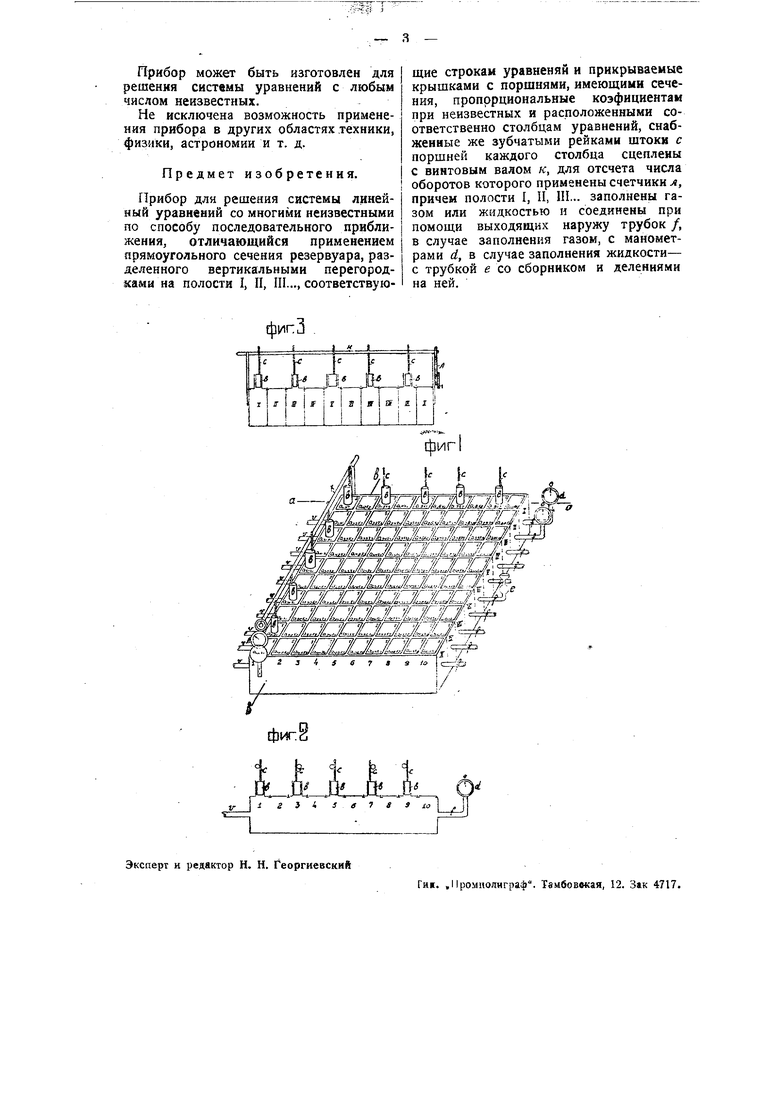
На чертеже фиг. 1 изображает общий внещний вид прибора; фиг. 2 разрез по линии аа фиг. 1, и фиг. 3-разрез по линии &б фиг. 1.
Метематически метод последовательного приближения заключается в следующем. Пусть дана система уравнений с п неизвестными:
. 4-+
+ PI
It -t
v;- +«г ;-Ьйгд-«л +
Рг
4-й
nJct
t, 1 + + ++
+ « -««++ Pf
, - ni 2+ nз з-r+
-г-t-e«n -Р«
1олагаем все коэфициенты первой строки, за исключением а, равными 0. Делим р. на а, получаем первое приPI
блнжение х -. Подставляем значение х во второе уравнение и считаем
(502)
коэфициенты в этом уравнения, начиная с й„, и т. д., равными 0. Получаем первое
Р„ о Xj
приближение x.,i -- ;
ставляем значение х и х, ь треьте уравнеРя- аЛ- аг г
ние, получим значение .х;,-
И Т. Д. дойдем до первого приближения х, Таким образом, получим первое приближение всех неизвестных. После этого делаем второй круг. Подставляем полученное значение неизвестных в первое уравнение, за исключением х, которое является искомым и, решая уравнение относительно ж, получим второе приближение x, вд
И Т. Д. Три-четыре круговых подстановки дают практически достаточную точность полученных значений неизвестных. Этот прием дает быстрое решение, и особенно в случае большой разницы между диагональными и побочными коэфициентами, но все же требует большого количества арифметических действий.
Предлагаемый прибор построен на этом простом математическом принципе решения уравнений. Каждый член уравнения можно рассматривать, как иексторый объем газа или жидкости; тогда сумма членов уравнения даст объем, равный свободному члену. Если примем величину коэфициента при неизвестном за площадь круга сечения цилиндра соответствующего диаметра, то высота этого цилиндра будет равна величине неизвестной.
Представим себе ящик (фиг. 3), разделенный вертикальными перегородками на части, отделяющие как бы строчки уравнения одну от другой-I, II. II и т. д. По горизонтальному направлению каждой сгрочки по количеству неизвестных на крышке ящика имеются отверстия s, плотно закрываемые крышкой (фиг. 1). Каждое из отверстий соответствует, таким образом, одному члену уравнения , и т. д.
Имея запас соответствующих крыщек с уже вделанными в них цилиндрами 1 н поршнями со штоком с, на котором имеется резьба, мы можем набрать наше уравнение по заданной схеме, т. е. вставить соответствующие номера крышек с цилиндрами. Практически, если считать отношение коэфициентов уравнения равным 50-ти, то достаточно иметь 50 разновидностей крышек, с разницей в площадях О, 1 м; шток к поршню цилиндра прикреплен эксцентрично. Набрав уравнение, впускаем в каждое отделение коробкя I, II, III и т. д. через трубки -и или газ или жидкость. С правой стороны прибора из каждого деления ящика выходят трубки /, оканчивающиеся, в случае применения газа, манометром rf, а в случае жидкости- трубкой е с делениями и двумя уширителями (сборниками). Уровень жидкости должен быть доведен 6 трубке до отчетного нуля, а в случае газа-манометры должны показать одно и то же давление. Свободные члены ставим добавлением в соответствующие воронки жидкости по объему, равному свободному члену, или увеличиваем на соответствующее давление, тождественное свободному члену, показание манометра путем введения добавочного газа в коробку.
Каждый из штоков с поршня соединяется резьбой с общим винтом к, идущим по направлению столбцов. Этих винтов будет столько, сколько столбцов
уравнения 1, 2, 3, 4, 5 и т. д. Каждый виит имеет на фасаде коробки систему колес л с циферблатами. Вращение винта дает показание высоты опускания или поднимания всех поршней цилиндров соответствующего столбца. При вращении винта вправо, в случае, если шток стоит справа по отношению к винту, поршень будет опускаться, если же шток стоит слева по отношению к винту, тог поршень будет подниматься. Это соответствует знакам коэфициентов при неизвестных, и крышки с цилиндрами и поршнями устанавливаются согласно этому правилу. Вращение винта вызовет опускание одних и поднятие других поршней, что изменит объем или жидкости или газа в коробках, и жидкость в соответствующих трубках займет положение или выше или ниже условного нуля; в случае газа манометры дадут отклонение.
По установке прибора начинается решение. Вращаем первый винт в ту или другую сторону так, чтобы манометр первой коробки дал показание условного нуля. После этого вращаем второй винт так, чтобы показатель второй коробки, который изменился вследствие вращения iiepвого винта, дал опять принятую условную отметку и т. д. до л-го винта. Показатели циферблатов (счетчики) дают первое приближение значения неизвестных. Переходя опять к первому винту и продолжая тот же прием до последнего, получим на циферблатах вторые значения неизвестных и т. д. Достаточно три - четыре приближения, чтобы уравнять показания манометров или трубок (в случае жидкости), и тогда отсчеты на циферблатах дадут окончательное значение неизвестных.
Этот прибор может быть с успехом применен для расчета статически неопределимых систем в рамных конструкциях.
Необходимая степень точности может быть получена в зависимости от конструктивного оформления прибора и его назначения в соответствии с выбором надлежащей жидкости или газа и точности показаний. Не исключена возможность применения изложенного принципа на изменении количества электроэнергии.

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для определения уровня жидкости в скважинах | 1928 |
|
SU16561A1 |
| Прибор для решения системы линейных алгебраических уравнений методом последовательных приближений | 1933 |
|
SU36704A1 |
| Гидропневматический пульсатор для испытания материалов на сжатие и растяжение | 1932 |
|
SU44709A1 |
| Гидравлические вагонные весы | 1934 |
|
SU50277A1 |
| Устройство для дистанционной сигнализации и автоматического регулирования механизмов | 1939 |
|
SU58012A1 |
| УСТРОЙСТВО ДЛЯ АВТОМАТИЧЕСКОГО ПРОИЗВОДСТВА ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ | 1932 |
|
SU36063A1 |
| Прибор для численного решения системы линейных алгебраических уравнений | 1941 |
|
SU68358A1 |
| Передвижной гидравлический кирпичный пресс | 1933 |
|
SU44516A1 |
| Прибор для решения систему линейных уравнений | 1931 |
|
SU37908A1 |
| Пневмогидравлический аккумулятор давления | 1927 |
|
SU14553A1 |



Авторы
Даты
1934-05-31—Публикация
1933-02-28—Подача