TilpH изучении технических вопросов очень часто возникает необходимость в решении системы линейных уравнений со многими неизвестными, как, например, в строительной механике, в которой всякая статически-неопределимая задача приводится к системе линейных уравнений; в особенности это относится к современным сложным рамным конструкциям, в которых число так называемых лишних неизвестных часто достигает нескольких десятков. Другим примером может служить теория уравновешивания ошибок по способу наименьших квадратов, находящая себе применение при всевозможных экспериментальных исследованиях, опытных наблюдениях и др.
Решение системы с большим числом неизвестных, нетрудное с теоретической точки зрения, на практике является крайне утомительной и трудной работой, требующей большого внимания, крайней осторожности в отношении допускаемых приближений, требующей непрерывного контроля на всем протяжении расчета, специальных приемов (метод Гаусса) и огромной затраты времени.
Графические методы невполне разрешают эту задачу, так как они пригодны только для трехчленных и пятичленных уравнений. С целью упрощения решений
указанных систем уравнений известны приборы с применением кинематической цепи в виде системы многоугольников с устанавливаемыми параллельно сторонами. В подобных приборах предлагается вершины многоугольников устраивать принудительно передвижными по параллельным прямым, причем с такой степенью свободы, что, после перенесения на прибор всех коэфициентов и свободных членов данной системы уравнений, вся цепь принимает положение, дающее решение данной системы уравнений.
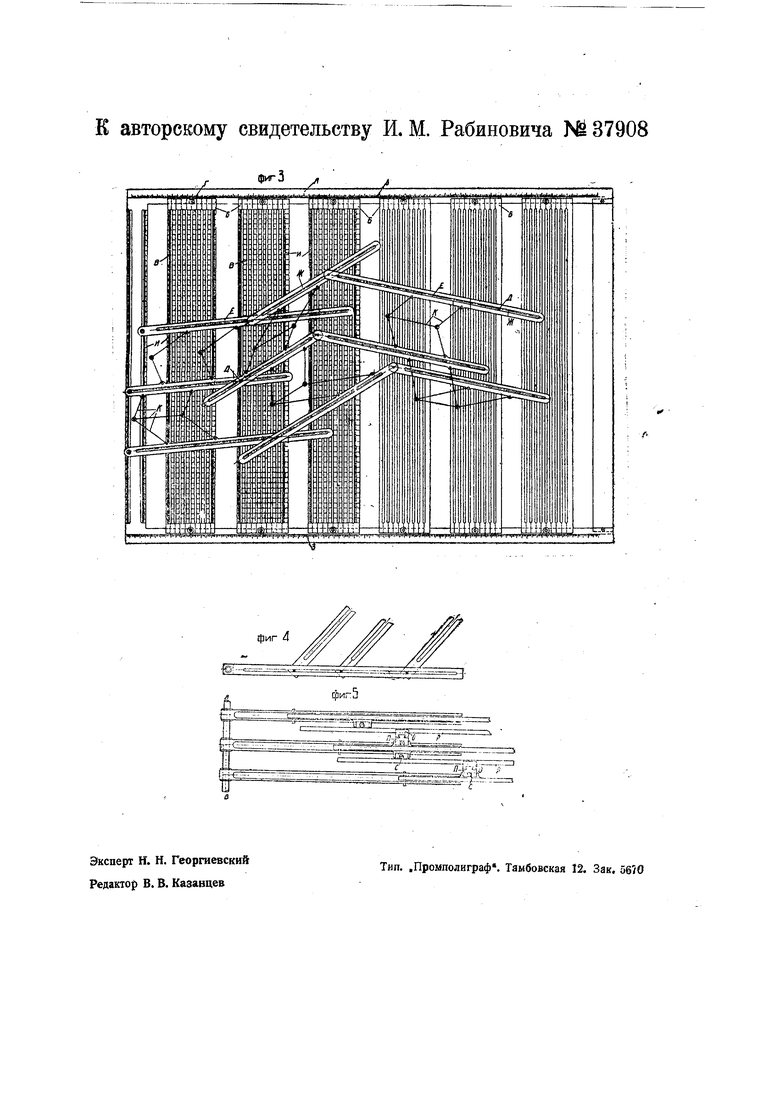
На чертеже фиг. 1 изображает схему плоского многоугольника; фиг. 2-то же нескольких плоских многоугольников; фиг. 3-вид плоской модели предлагаемого прибора; фиг. 4 и 5-вид части пространственной модели прибора в двух проекциях.
Предлагаемый прибор основан на нижеследующем рассуждении. Если у плоского многоугольника ACEGK (фиг. 1) точка А неподвижна, а вершины С, E,.G, К могут скользить по неподвижным вертикальным прямым /-1, 2-2, 3-3 ... то длины сторон многоугольника будут при этом изменяться. Цели обозначить углы наклона этих сторон к горизонтали
а расстояния
через pi, 2.
г и между осями-через а, а, , . , %„, то CD flu tg f Oil ctg F aigtga fliaCtg-r ; G ai3tg 3 :fli3CtgT3; KB ,..a cgt T. i- 1i 1 Обозначая tg 9i ctg т, Xi, ctgT2 A;2 . . . . . . ctgt х„, можно уравнение (1) переписать в следующем виде «П l + «12 + + «13 -«in- n io -(2) На этом основании можно сказать, что рассматриваемый многоугольник, имеющий п подвижных узлов, является кинематический изображением линейного уравнения (2) с неизвестными х Xg . . . х. Кинематическая цепь (или геометрическая фигура), АСЕ. . , К имеет п степеней свободы, так как ее положение определяется независимыми вертикальными перемещениями ее п узлов. Если считать длину RB (т. е. правую часть уравнений (2) постоянной, то степень свободы цепи снизится на единицу и будет равна п - 1. На фяг. 2 изображены т аналогичных многоугольников; стороны каждого из них могут скользить по соответствующим заданным п вертикальным осям, расстояния между которыми обозначены вообще через а.. Если считать, что крайние правые концы всех этих многоугольников занимают заданные положения, то степень свободы всей этой кинематической цепи будет равна (л-1) т. Если каким-либо способом устроить так, чтобы стороны всех многоугольников, обозначенные одними и теми же цифрами, оставались всегда параллельными между собою, как это и показано на фиг. 2, то при я /и система уравнений становится определенной. Этому соответствует и степень свободы кинематической цепи, равная п - /те - 0. Таким образом в случае определенной системы линейных уравнений кинематическая цепь превращается в неизменяемую фигуру. Иллюстрирующая возможность практического применения прибора модель последнего (фиг. 3) состоит из рамы А, в которой расположены ползуны Б, снабженные параллельными щелями В и зажимаемые в требуемом на раме А положении баращками Г, В соответствующие щели вставлены щтифты Д, которые служат щарнирами для сторон Е кинематической цепи. Каждая сторона имеет на одном из своих концов круглое отверстие для штифта, и в средней своей части продольную щель Ж, которая позволяет передвигаться в ней штифту сочлененной стороны. Благодаря этой щели, длины сторон кинематической цепи во время ее движения могут измениться. Шкалы 3 рамы предназначены для облегчения точного подбора коэфициентов йц, «12. 22 и т. д., а шкалы U- для отсчета длины вертикальных катетов СД, EF и т. д. (фиг 1). Для обеспечения параллелизма между одноименными сторонами многоугольников, между ними расположены связывающие их дополнительные пятизвенные шарнирные цепи Л,каждая из которых, будучи шарнирно связана с дзумя сторонами основной цепи, образует с ними два параллелограма, имеющих одну общую сторону. Помимо обеспечения параллелизма сторон, такая пятизвенная цепь налагает на движение основной цепи только одну связь: добавление среднего звена вносит три степени свободы, а шарнирное присоединение четырех боковых стержней вносит четыре связи; в итоге получается 4 - связь. Эта связь и состоит в уничтожении взаимных угловых перемещений обоих соединяемых стержней основной цепи; что же касается взаимных линейных перемещений, то они остаются свободными. В пространственной модели фиг. 4 и 5 все многоугольники расположены не в одной, а в нескольких параллельных между собою плоскостях. Стороны всех многоугольников,, изображающие неизвестную х, насажены наглухо на общую ось, так что их оси лежат в одной плоскости, причем так, чтобы при любом угле поворота оси все эти стороны повернулись на тот же угол. Таким образом здесь не требуется никакой дополнительной кинематической цепи для сохранения параллелизма между сторонами. Для сохранения параллелизма между. остальными сторонами служат соединительные детали в виде двух поступательных пар, состоящих из тела О, снабженного на двух гранях взаимноперпендикулярными прорезами, в которые вставлены ползуны /7, Р. Ползуны, вставленные в одно и то же тело О, могут иметь друг относительно друга любое поступательное движение, а поворачиваться один относительно другого не могут. При помощи зажимов, снабженных винтом С, эти ползуны прикрепляются к соединяемым сторонам, заставляя их сохранять взаимный параллелизм.
При таком устрсЙ1Стве прибор может состоять из отдельных секций, каждая из которых предназначается для системы уравнений с числом неизвестных, не превышающим, например, 5 иЛи 6.
Увеличение числа неизвестных сверх предельного для данной секции числа «требует увеличения: 1) числа многоугольников, 2) числа сторон в каждом из них.
Прибор допускает следующее обобщение. Прямолинейные параллельные траектории узлов многоугольников могут быть заменены наклонными непараллельными между собой прямыми или даже кривыми линиями. Для этого необходимо соответствующим образом перестроить щели В (фиг. 3), в которых скользят узловые штифты.
Для численного решения, например, системы п уравнений с п наизвестными, все ее коэфициенты и свободные члены, выраженные в числах, откладываются ползунками Б по шкалам 3 рамы А (фиг. 3). После установки ползунков по шкалам U отсчитываются длины катетов СДу EF и т. д. (фиг. 1), а затем путем деления на основание АД, CF-находятся неизвестные. Автором имеется в виду решение также определенной системы линейных уравнений в случае, когда все или некоторые свободные члены даны в буквенном виде, определение фокусных отношений, нахождение условий обращения детерминанта в нуль, решение неопределенной системы линейных уравнений и т. д.
Предмет изобретения.
Прибор для решения системы линейных уравнений с применением кинематической цепи в виде системы многоугольников с устанавливаемыми параллельно сторонами, отличающийся тем, что вершины многоугольников устроены передвижными принудительно по параллельным прямым с такою степенью свободы, что после окончания операций, заключающихся в перенесении на прибор всех коэфициентов и свободных членов данной системы уравнений, вся цепь принимает положение, дающее решение системы уравнений.


| название | год | авторы | номер документа |
|---|---|---|---|
| Прибор для решения системы линейных уравнений | 1932 |
|
SU37909A1 |
| ЭЛЕКТРИЧЕСКОЕ УСТРОЙСТВО ДЛЯ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ВЫСШИХ СТЕПЕНЕЙ С ОДНИМ НЕИЗВЕСТНЫМ | 1931 |
|
SU38358A1 |
| Прибор для численного решения системы линейных алгебраических уравнений | 1941 |
|
SU68358A1 |
| УСТРОЙСТВО ДЛЯ АВТОМАТИЧЕСКОГО ПРОИЗВОДСТВА ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ | 1932 |
|
SU36063A1 |
| Устройство для решения системы алгебраических линейных уравнений | 1945 |
|
SU68083A1 |
| Устройство для решения дифференциальных уравнений | 1937 |
|
SU57020A1 |
| Машина для решения уравнений высших степеней с одним неизвестным | 1934 |
|
SU49497A1 |
| Прибор для решения системы линейных уравнений | 1933 |
|
SU36706A1 |
| Прибор для решения системы линейных алгебраических уравнений методом последовательных приближений | 1933 |
|
SU36704A1 |
| Прибор для решения дифференциальных уравнений | 1936 |
|
SU53526A1 |


.ве I
i i

Авторы
Даты
1934-07-31—Публикация
1931-08-09—Подача