Изобретение относится к области вычислительной техники и может быть применено для моделирования систем обыкновенных дифференциальных уравиений, содержаш,их произвольные функции многих переменных и требующих решения в реальном масштабе времени. Известно цифро-аналоговое устройство для Моделнрования обыкновенных дифференциальных уравнений, построенное на базе цифровой вычислительной машины, аналого-цифровых преобразователей, аналоговых сумматоров, цифровых управляемых сопротив лений, суммирующих усилителей, аналоговых запоминающих устройств и ключей. Однако контур моделирования дифференциальных уравнений является разомкнутым, что приводит к необходимости проверки в каждом цикле решения условия работы цифро-аналогового устройства в реальном масштабе времени, где Гц.- время, затрачиваемое цифровой вычислительной машиной «а вычисление переменных коэффициентов, нелинейные преобразования, выдачу коэффициентов на цифровые управляемые сопротивления и преобразователями «аналог-код и «код-аналог ; At - доиустимая дискретность квантования аналоговых сигналов. Многократные пересылки из аналоговой части устройства в цифровую и наоборот составляют значительную долю одного цикла решения. Стремление получить решение в реальном масштабе времени однозначно накладывает повышение требования к быстродействию ЦВМ и преобразователям. Кроме того, отмечается наличие постоянного запазды.вания при вычислении суммарного напряжения обратных связей и правой части одного уравнения системы отио.ситсльио другого, что приводит к необходимост проведе1 ия в процессе решения дополнительного исследования на устойчивость решения. В предлагаемом гибридном устройстве для моделирования систем обыкновенных дифференциальных уравнений, содержащих произвольные функции одной и двух (в общем случае п) переменных, в реальном масштабе времени для воспроизведения нелинейиых функций введены гибридные модули. Выход каждого аналогового интегратора соединен с аналоговым делителем гибридного модуля, входы цифро-аналоговых преобразователей и цифровых управляемых сопротивлений каждого гибридного модуля связаны с выходом цифовой вычислительной машины, выход аналогового усилителя, цифро-аналогового преобразователя н цифрового управляемого сопротивления каждого гиб.ридного модуля соединен с суммирующим усилителем, а выход каждого гибридного модуля через аналоговые сумматоры и блоки перемножения - -со входами аналоговых н.итеграторов.
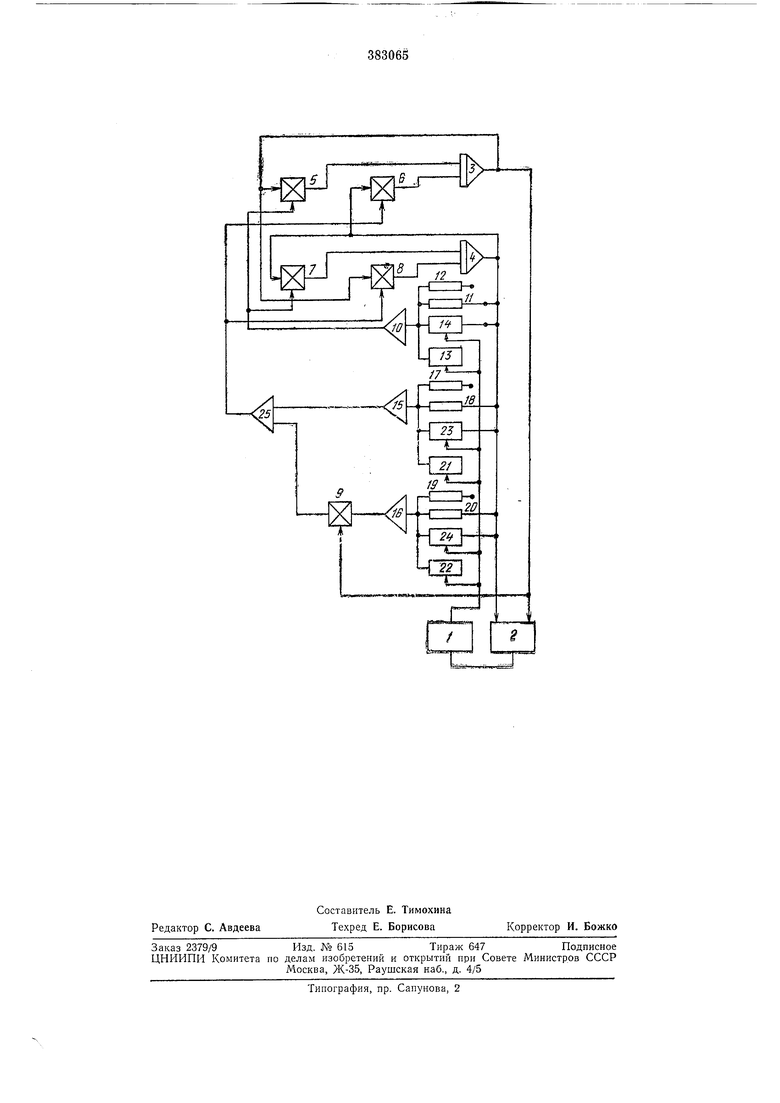
На чертеже представлена блок-схема предлагаемого устройства.
Устройство состоит из цифрового вычислительного блока /, аналого-цифрового преобразователя 2, аналоговых интеграторов 3 и 4, блоков умножения 5-9, гибридного функционального преобразователя для произвольной функции одной переменной. Последний включает аналоговый усилитель 10, аналоговые делители напряжения 11 и J2, цифро-аналоговый преобразователь 13 и цифровой управляемый резистор 14. Кроме того, устройство содержит гибридные функциональные преобразователи для произвольных функций двух переменных, состоящие из аналоговых усилителей /5 и 16, аналоговых делителей напряжения 17, 18, 19 и 20, цифро-аналоговых преобразователей 2, 22, цифровых управляемых резисторов 23 и 24 и усилителя 25.
Предлагаемое устройство позволяет моделировать систему двух дифференциальных уравнений первого порядка (порядок решаемых уравнений не превыщает количества интеграторов), содержащих произвольные функции одной и двух (в общем случае) переменных, в реальном масштабе времени, когда все переменные являются быстроизменяюи1,имися величинами.
Рассмотрим в качестве примера моделирование следуюшей системы уравнений:
dx
(y)-x + a,f (х,у)-у
- bJ(y)-y + b,.f{x,y}-x df
Требуемый ноложительный эффект достигается в результате того, что законы изменения переменных коэффициентов и нелинейные преобразования воспроизводятся иа гибридных модулях. Операции интегрирования, умпожеиия на постоянный -коэффициент и перемножения быстроизменяющихся переменных производятся аналоговыми элементами. Путем «замораживания ряда коэффициентов исходных нелинейных функций на значениях, соответствующих наиболее часто встречающимся (обычно линейных), образуются линейные части произвольных функций, которые моделируются на аналоговых элементах гибридиых модулей. Цифровая вычислительная М1ащина вводит поправки, являющиеся разностями между линейными и текущими значениями функции. Благодаря этому все быстроизмеияющиеся переменные (вернее линейные части их значений) замыкаются в непрерывной части устройства и в замкнутые .контуры не вносятся запаздывания, что позволяет моделировать системы обыкновенных дифференциальных уравнений, содержащих произвольные функции одной и двух (в общем случае п) пе ременных в реальном м асштабе времени, -когда все переменные являются быстроизменяющимися величинами.
Для воспроизведения произвольной функции одной переменной на гибридном модуле она представляется следующим образом:
f(y) aty + bi, (/г у у,-..; i,(3)
где У{, t/j+i - значения точек аргумента у, в
которых задается функция; ui--наклон отрезка прямой в пределах указанного интервала изменения у;
bi - отрезок, отсекаемый продолже|Нием этой прямой на оси ординат, также соответствующий указанному интервалу.
Таким образом, уравнение (3) реализует линейную интерполяцию.
Согласно вышеизложенному формулу (3) можно записать в виде:
f(y) (a + M,)y + (b + Ab),
(4)
где а, b - «замороженные значения коэффициентов QI и Ьг, соответствующие наиболее часто встречающимся; Аи,, Лиг - коэффициенты коррекции, равные соответственно (а-а,-) и (Ь-Ь,).
Схема работает следующим образом. Аналоговое напряжение поступает на делитель напряжения 11 и цифро-аналоговый преобразователь 13, с выходов которых снимаются соответственно напряжения ау и и. До тех пор, ;пока у остается в пределах выбранною интервала, выходная цифровая информацля
не требуется, то есть Даг 0 и А&г 0. При переходе на новый участок ( или ) на цифро-аналоговый преобразователь 13 и цифровой управляемый резистор 14 выдаются коэффициенты коррекции, которые, суммируясь с выбранными постоянными коэффициентами, образуют новые значения наклона и огрезка на оси ординат. В результате на выходе блока 5 .получаем значение функции f(y). Произвольная функция двух перемепных
представляется но аналогии в следующем виде:
I (х,у) -- (а + Аа) у + (Ь + А6,.) +
+ (c + Ci:)y + (d + M,(5)
Схема работает следующим образом. Аналоговое напряжение у поступает па в.ходы аналоговых делителей 18 и 20 и цифровых управляемых резисторов 23 и 24. На входы аналоговых делителей 17, 19 и ацалоговые .входы цифро-аиалогооых прео бразователей 21, 22 подается опорное напряжение.
Если переменные х у находятся на линейном интервале, коэффициенты коррекции Да,,-, A&ij/ .Cij, Adij равны нулю. При переходе х
у на нелинейные участки указанные коэффициенты имеют определенное значение.
В результате, на выходах суммирующих усилителей 15 и 16 образуются суммЫ
(а + Да,.)|/Ч-(6 + Д6,.) и ( + Ac,.)y + (d + )
Выход усилителя 16 соединен с одним из выходов блока умножения 9, на другой вход которого подается апалоговое напряжение х. Суммируя значения напряжений с выходов усилителя 15 и блока умножения 9, на усилителе 25 получаем значение функции f(Xiy).
Предмет изобретения
1. Устройство для моделирования систем дифференциальных уравнений, содержащее цифровой вычислительный блок, аналого-цифровой преобразователь, блоки умножения, сумматоры и интеграторы, отличающееся тем, что, с целью увеличения точности и быстродействия устройства, а также повыщения его надежности, оно содержит гибридные, функциональные преобразователи, первые входы которых соединены с цифровым вычислительным блоком, вторые входы подключены к выходу первого интегратора и ко входу аналого-цифрового преобразователя, а выход первого гибридного функционального преобразователя через первый блок умнол ения, соединен11ый с аналого-цифровым преобразователем, подключен к первому входу сумматора, ко второму входу которого подсоединен выход второго гибридного функционального преобразователя, выход сумматора через второй и третий блоки умножения подключен к первым входам первого и второго интегратора, выход
третьего гибридного функционального преобразователя через четвертый и пятый блоки умножения подключен ко вторым входам первого и второго интеграторов, а выход второго интегратора -подключен к аналого-цифровому
преобразователю,
2. Устройство по п. 1, отличающееся тем, что в нем гибридные функциональные преобразователи выполнены в виде операционного усилителя, ко входу которого подключены параллельно соединенные делитель напряжения, соединенный со вторым ВХОДОМ1 гибридного функционального преобразователя, цифровой управляемый резистор, связанный со вторым входом гибридного функционального преобразователя и аналого-цифровой преобразователь, соединенный с первым входом гибридного функционального преобразователя, а выход операционного усилителя соединен с выходом гибридного функционального преобразователя.


| название | год | авторы | номер документа |
|---|---|---|---|
| :.;::?ООЮЗНАЯ•'^''::\r'?j''EOPlJ| | 1973 |
|
SU392510A1 |
| Аналого-цифровая вычислительная система | 1987 |
|
SU1509955A1 |
| УСТРОЙСТВО ИЗМЕРЕНИЯ ПАРАМЕТРОВ ВОЛНЕНИЯ | 2012 |
|
RU2489731C1 |
| Устройство для решения систем линейных алгебраических уравнений | 1975 |
|
SU546907A1 |
| Устройство для решения линейных систем алгебраических уравнений | 1985 |
|
SU1325464A1 |
| Аналого-цифровое устройство для решения системы дифференциальных уравнений | 1987 |
|
SU1462378A1 |
| Функциональный преобразователь | 1985 |
|
SU1357938A2 |
| УПРАВЛЯЮЩИЙ АППАРАТНО-ПРОГРАММНЫЙ КОМПЛЕКС ДЛЯ ОБРАБОТКИ РАДИОЛОКАЦИОННОЙ ИНФОРМАЦИИ | 2001 |
|
RU2222028C2 |
| УСТРОЙСТВО ДЛЯ ВОСПРОИЗВЕДЕНИЯ ОРТОГОНАЛЬНЫХ ФУНКЦИЙ | 2005 |
|
RU2282891C1 |
| Аналого-цифровой преобразователь интегральных характеристик напряжений | 1988 |
|
SU1615888A1 |


Авторы
Даты
1973-01-01—Публикация