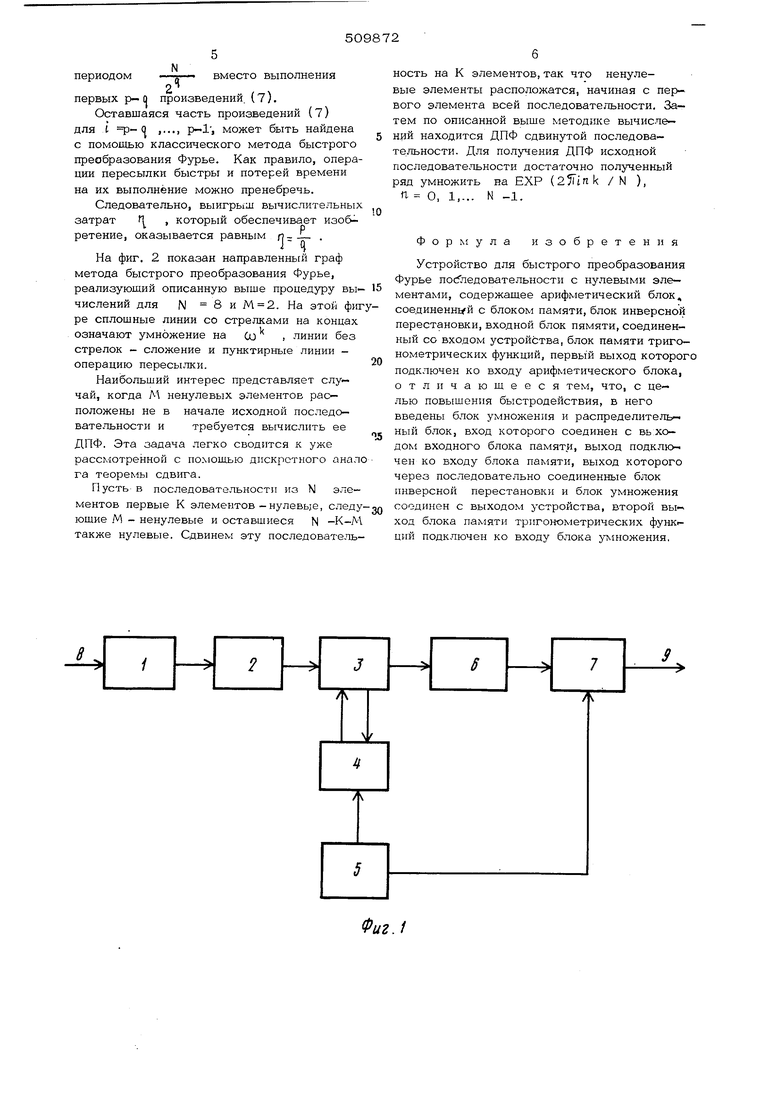
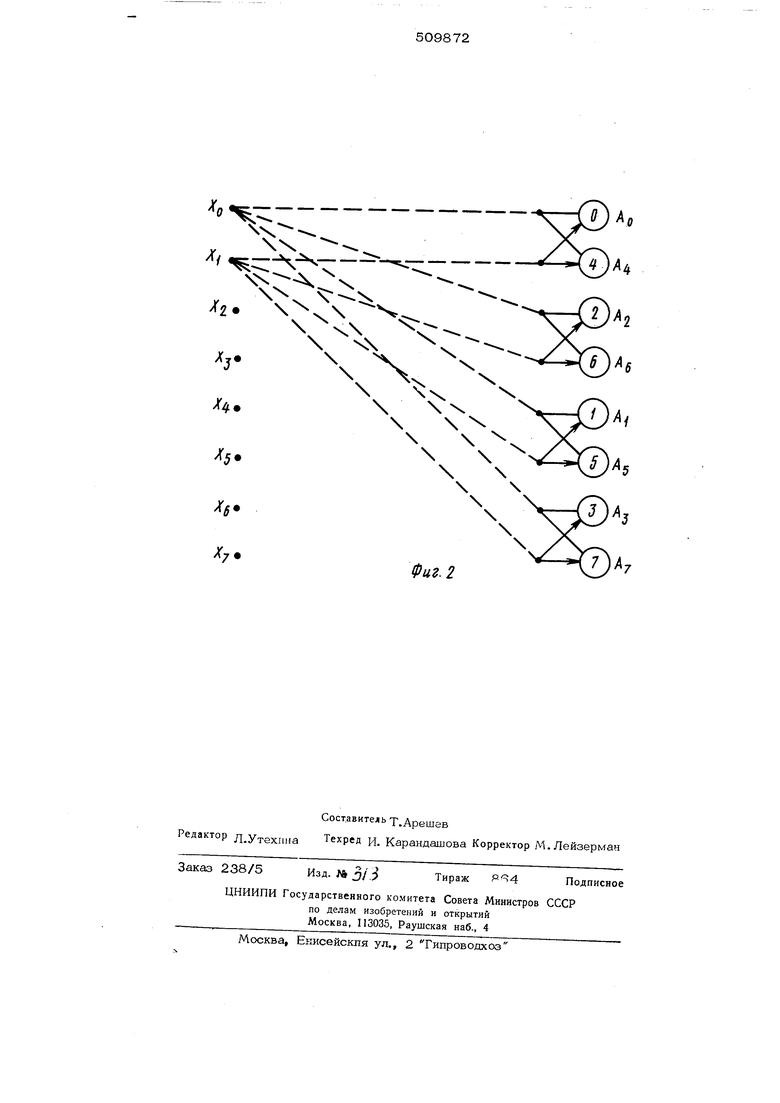
Ненулевые элементы последовательности от которой вычисляется ДПФ, поступают во входной блок памяти 1 и затем в распределительный блок 2, который осуществляет в блоке памяти 3 периодическое продолжение ненулевой части последовательности на всю последовательность, начиная с первого элв мента с периодом, равным минимальной сте пени двух, равной числу нулевых эламелтов или превосходящей его, Арифметический блок 4 выполняет стандартные арифметические операции сложе ния и умножения над элементами исходной последовательности, хранящимися в блоке 3 памяти и значениями тригонометрических функций, взятых из блока .5 памяти тригонометрических функций. После завершения вычислений, полученные коэффициенты ДПФ упорадочиваются в блоке 6 инверсной перестановки и поступают в блок умножения 1, на. второй вход которого поданы значения тригонометрических функций, аргумент которых зависит от сдвига ненулевой части ис ходной последовательности относительно первого элемента этой последовательности. Для последовательности N равномерно расположенных элементов Х, П - О, 1, 2,..., N -1. ДПФ определяется выражением vN-1,, (1) Ч 1 ,.« k Ki2i л„СО где k О, 1, 2,..., -1; N Или в матричной форме А. - W X. где А (А, А ,..,, А); X ( (N-1)(N-1) Ограничимся далее случаем, когда 1 2Р, Р О, 1, 2,.., Обычный метод вычисления ДПФ от последовательности из N элементов, называемый прореживанием исходного ря по времени, сводится к факторизации ма рицы преобразования VV и представлен ее с точностью до порядка расположени строк в виде w F 2-lll ,1,... р-1 Матрица, составленная из подматриц Aj, k О, 1,..,2-1 где вместо нулевых элементов, как и в выражении (4), оставлены пропуски. Показатели степени, взятые в кружки, означают, что для получения показателя степени необходимо выполнить двойную инверсию над цифрой, записанной в кружке и представленной в двоичной форме ( например, при N 8 и 011 имеет К ). Факторизация матрицы преобразования приводит к перестановке получаемых коэффициентов Фурье согласно двоичной инверсии номеров этих коэффициентов. Рассмотрим теперь класс исходных последовательностей X , содержащих часть нулевых элементов, т, е, таких, как ГХ О для п О, 1,,,,, М-1 |Х„ О для П м, Л1 + 1,,,., N -1, где М удовлетворяет условию М Л. 2 Определим 1 -и щаг вычислительной процедуры в виде А j F . А F.X; t 1, 2,..., Р-1. Тогда результат Р..- С| 1„го шага вычислительной процедуры можно записать в форме вектора А p-q-1 «- Vq-i -- M-i0.-0.j.l -й-О,...; 01 причем х.. X N N-.n , Таким образом, вектор Аможно образовать из вектора X периодическим продолжением ненулевых элементов X с N вместо выполнения периодом - первых р- о произведений {7). Оставшаяся часть произведений (7) для i р- (J ,..., р-1, может быть найдена с помощью классического метода быстрого преобразования Фурье. Как правило, опера ции пересылки быстры и потерей времени на их выполнение можно пренебречь. Следовательно, выигрыш вычислительных затрат 1 , который обеспечивает изобретение, оказывается равным л-- . На фиг. 2 показан направленный граф метода быстрого преобразования Фурье, реализующий описанную выше процедуру вы числений для N 8 и . На этой фи ре сплошные линии со стрелками на концах означают умножение на Со , линии без стрелок - сложение и пунктирные линии операцию пересылки. Наибольший интерес представляет случай, когда М ненулевых элементов расположены не в начале исходной последовательности и требуется вычислить ее ДПФ. Эта задача легко сводится к уже рассмотренной с помошью дискретного анал га теоремы сдвига. Пусть в последовательности из N элементов первые К элементов-нулевые, след юшие М - ненулевые и оставшиеся N -К-М также нулевые. Сдвинем эту последователь ность на К элементов, так что ненулевые элементы расположатся, начиная с первого элемента всей последовательности. Затем по описанной выше методике вычислений находится ДПФ сдвинутой последовательности. Для получения ДПФ исходной последовательности достаточно полученный ряд умножить на ЕХР (ZJtink / N ), П. О, 1,... N -1. Формула изобретения Устройство для быстрого преобразования Фурье пос5ледовательности с нулевыми элементами, содержашее арифметический блок, соединенней с блоком памяти, блок инверсной перестановки, входной блок пямяти, соединенный со входом устройства, блок памяти тригонометрических функций, первый выход которого подключен ко входу арифметического блока, отличаюшееся тем, что, с целью повышения быстродействия, в него введены блок умножения и распределитель- ный блок, вход которого соединен с вь:хо- дом входного блока памяти, выход подключен ко входу блока памяти, выход которого через последовательно соединенные блок инверсной перестановки и блок умножения соодинен с выходом устройства, второй выход блока памяти тригонометрических функ ций подключен ко входу блока умножения.

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления коэффициентов дискретного преобразования фурье | 1974 |
|
SU506883A1 |
| Устройство для быстрого преобразования Фурье-последовательности с нулевыми элементами | 1981 |
|
SU1005070A1 |
| Устройство для быстрого преобразования Фурье последовательности с нулевыми элементами | 1980 |
|
SU896631A1 |
| Каскадное устройство для быстрого преобразования Фурье | 1983 |
|
SU1265794A1 |
| Анализатор спектра Фурье | 1984 |
|
SU1226486A1 |
| Способ и устройство формирования физического спектра сигнала | 2017 |
|
RU2666321C1 |
| Устройство для вычисления коэффициентов дискретного преобразования Фурье | 1979 |
|
SU877556A1 |
| АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ | 1991 |
|
RU2015550C1 |
| Устройство для вычисления спектра Фурье | 1983 |
|
SU1121678A1 |
| Устройство для вычисления коэффициентов Фурье | 1979 |
|
SU926668A1 |


ff
-
/
-
/ V
fe./
Авторы
Даты
1976-04-05—Публикация
1974-04-05—Подача