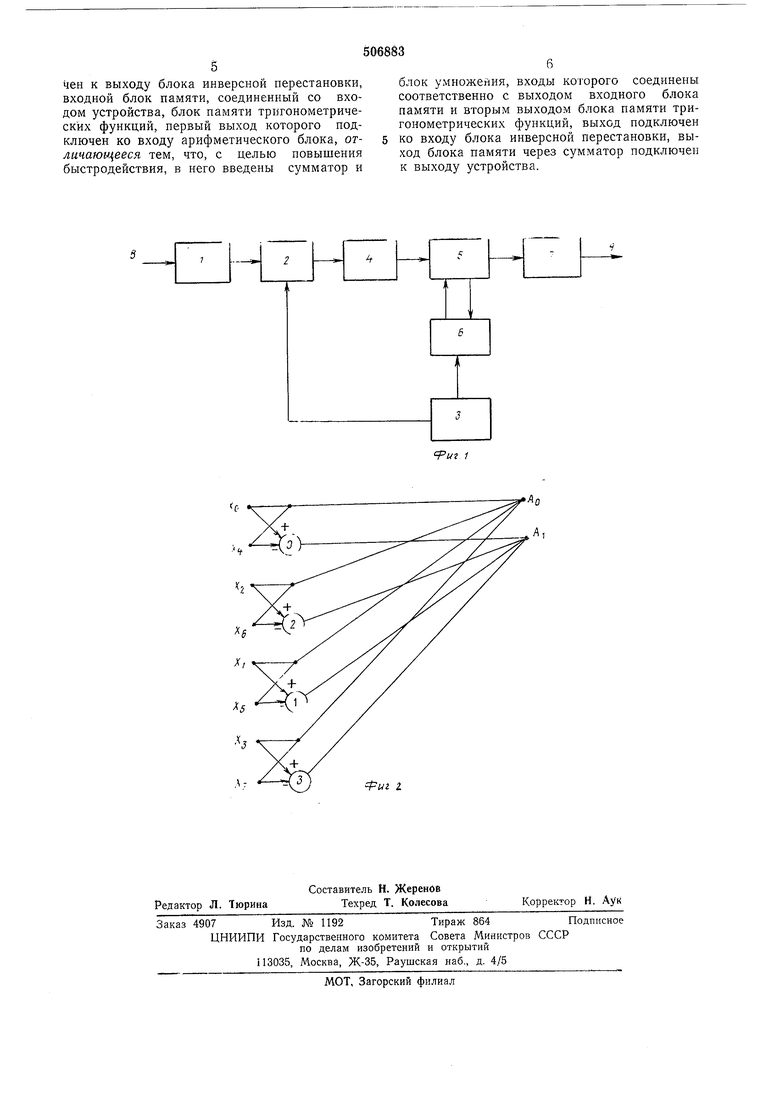
ментами и значениями тригонометрических функций из блока 3 арифметический блок 6 вынолняет стандартные арифметические онерацин типа умножения и сложения. К выходным каналам блока 5 памяти подключен сумматор 7, число каналов которого равно отношению количества элементов исходной последовательности к минимально возможной целой положительной степени двух, равной или превосходящей число требуемых коэффициентов преобразования Фурье. Аргумент тригонометрических функций, поступающих на второй вход блока 2, зависит от сдвига требуемых коэффициентов относительно нулевого коэффициента и в том случае, когда искомая часть коэффициентов расположена начиная с нулевого элемента, блок 2 не участвует в работе. Дискретное преобразование Фурье последовательности х„ , гг 0,1,.-.., . равномерно расположенных элементов дается выражениемЛ - W-X, Лл-1 ) - вектор коэффигде Л т (Ло,Ль циентов Фурье; д;т (хо, Xi, д;л-1 ) - вектор исходной последовательности элементов. матрица преобразования. Ограничимся случаем N 2, р О, 1, 2,... Метод быстрого преобразования Фурье сводится к факторизации матрицы преобразования W и представлению ее с точностью до норядка расположения строк в виде W Ro-Ri- .. R,t,(3) t 0,l,...,p-l (4) , к 0,1,...,2-1 (о) ( со и, вместо пропусков, в матрицах R k подразумеваются нулевые элементы. Пусть требуется определить первые М коэффициентов AI , t 0,l, ...,Л1-1, где М удовлетворяет условию 20+1 - 2 Введем t-й Щаг вычислительной процедуры в виде Bp-i- R ,,-i- Вр-.{.:.-1 , где В,,,.-1 RP -1-х(7) г 2,3, ...,р Если на q-M шаге будет найден вектор В ,1 (bo, bi,..., b.:- ), то за оставшиеся р-q щагов будет найден вектор 81 Л (ЛоЛ1Лл--1 ) такой, что b Ml+i / о t 0,l,..., М-1 Таким образом, в том случае, когда требуется определить только первые М коэффициентов, последние р-q вычислительных щагов в классическом методе быстрого преобразования Фурье можно вычислять по формуле (8). При этом на вычисление вектора Л из Вр-(1 потребуется N операций комнлекс3ного сложения, вместо примерно- Л (р-д) арифметических комплексных операций типа сложения и умножения при обычном методе вычисления. На фиг. 2 показан направленный граф рассмотренного выше метода для N 8 и М 2. Здесь перестановку входных элементов согласно двоичной инверсии их номеров следует провести перед началом вычислений, затем необходимо выполнить один шаг классического метода быстрого преобразования Фурье и, наконец, вычислить суммы (8). Сплошные линии на фиг. 2 обозначают операции сложения, линии со стрелками на концах - операцию умножения. Показатели степени, взятые iB кружки, означают, что для получения показателя степени при со необходимо выполнить двоичную инверсию над номером, стоящим в кружке. Тот случай, когда требуется вычислить последовательность коэффициентов, расположенных подряд начиная с к-го номера сводится к уже рассмотренному с помощью дискретного аналога теоремы сдвига. При этом, исходная последовательность элементов должна быть умножена на ехр - и затем выполняются описанные выше вычисления. Требуемые М коэффициентов дискретного преобразования Фурье будут расположены начиная с нулевого элемента. Формула изобретения Устройство для вычисления коэффициентов дискретного преобразования Фурье, содержащее арифметический блок, соединенный с блоком памяти, вход которого подключен к выходу блока инверсной перестановки, входной блок памяти, соединенный со входом устройства, блок памяти тригонометрических функций, первый выход которого подключен ко входу арифметического блока, отличающееся тем, что, с целью повышения быстродействия, в него введены сумматор и
блок умножейия, входы которого соединены соответственно с выходом входного блока памяти и вторым выходом блока памяти тригонометрических функций, выход подключен ко входу блока инверсной перестановки, выход блока памяти через сумматор подключен к выходу устройства.

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для быстрого преобразова-ния фурье последовательности с нулевы-ми элементами | 1974 |
|
SU509872A1 |
| Устройство для быстрого преобразования Фурье-последовательности с нулевыми элементами | 1981 |
|
SU1005070A1 |
| Анализатор спектра Фурье | 1984 |
|
SU1226486A1 |
| Устройство для вычисления коэффициентов дискретного преобразования Фурье | 1979 |
|
SU877556A1 |
| Устройство для быстрого преобразования Фурье последовательности с нулевыми элементами | 1980 |
|
SU896631A1 |
| Генератор случайных чисел | 1981 |
|
SU981999A1 |
| Устройство для выполнения преобразования Фурье | 1980 |
|
SU928363A1 |
| Устройство для вычисления коэффициентов Фурье | 1985 |
|
SU1278886A1 |
| Цифровой анализатор энергетического спектра | 1978 |
|
SU769443A1 |
| Устройство для выполнения преобразования Фурье | 1987 |
|
SU1418747A1 |

. .
.7
иг г
Авторы
Даты
1976-03-15—Публикация
1974-04-05—Подача