Многие технические задачи из различных обласгей техники требуют для своего разрешения производства сложных и трудоемких математических вычислений.
Часто также, при математическом анализе тех или иных физических процессов, возникают столь большие трудности;, что приходится искать решений экспериментальным путем. Последний путь не всегда может быть оправдан, в особенности в условиях строительства, так как требует затраты времени и наличия специального оборудования.
В ранее известных соответствуюшдх приборах и механизмах для производства технических расчетов уже применялись диференциальные зубчатые блоки для связи между отсчетными индексами, расположенными в области и на контуре, например, в приборах для решения уравнений Лапласа.
Круг задач, решаемых с помош ью предлагаемого прибора методом Э. Шмидта, достаточно велик и определяется уравнением общего вида:
.(П
df - ,
Оно может быть представлено, в частности, уравнениями Фурье, Лапласа,
Покеля, Пуассона.
Достаточно указать, что в одной лишь области, связанной с теплотехническим строительством, представляются широкие возможности упрощения расчетов и вместе с тем повышения качества строительства.
Круг решаемых задач в этой области включает расчеты ограждающих теплоизоляционных устройств, выбор теплоизолирующих материалов, расчеты холодильников, термические расчеты мерзлых грунтов и т. д.
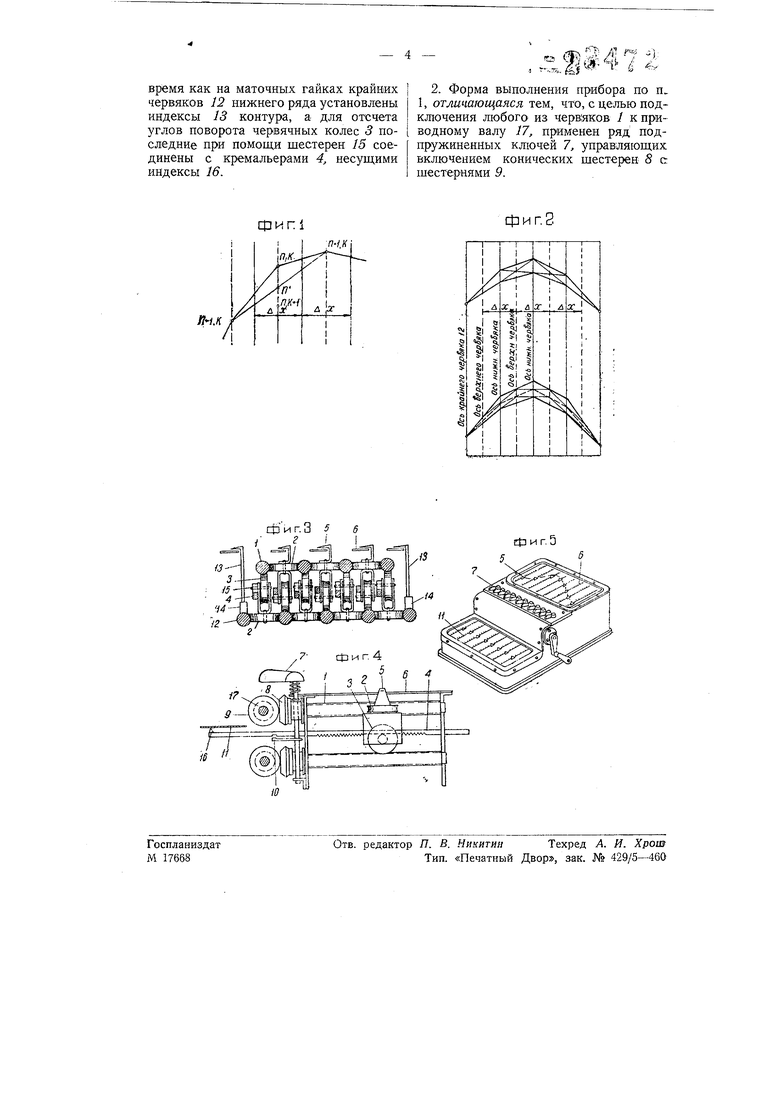
На чертеже фиг. I изображает диаграмму решения, предложенного уравнения; фиг. 2 - сравнительное графическое построение температурной кривой; фиг. 3 - схематический поперечный разрез механизма прибора; фиг. 4- пpiOдoльный разрез его; фиг. 5-перспективный вид прибора для решения уравнений указанного вида.
В основу кинематики решающего механизма положен графический метод решения уравнения Фурье, известный под именем предложившего его Э. Шмидта. Основное уравиение теплопровод ности Фурье: дТ д-Т каписанное в конечных разностях, со гласно фиг. 1, будет: , fe - л, fe+l , ., о I п+1, k Tn-i, fe -р /о - -( , где 2а множитель пропорци,ональности, а левая часть уравнения (3) представляет изменение температуры в слое за время (k + 1) - k Af. Свободным выбором Вгеличин Л f и .А X можно достичь любого соотношения между отрезком (n,k - лV и (n,k - - n,k 4-1). Беря их равными друг другу (по Э. Шмидту) получим множитель: (х)и™ Т. (Ах) благодаря чему упрощается графическая работа и положение точек дает температуру в середине слоя. В данном случае не было никакой необходимости при разработке кинематической схемы прибора сохранить в точности нриемы графического решения задач. Поэтому, по соображениям улучшения эксплоатационных качеств: прибора, множитель 2а взят равным половине, что дает М : - , т. е. величина промежутка времени Af в; данном случае в два раза меньше, чем прилятая при графическом методе. Выбор такой величины t дает более простую кинематическую схему механизма. Сравнительное графическое построение приведено на фиг. 2, где вверху дано лостроение температурной кривой при , а внизу при2а.:-2-. (ДЛГ) i (Дл:) Решение получают в виде отсчетов по шкалам, вдоль которых движутся индексы. При этом целиком сохраняется наглядность графического способа, заключаюш аяся в том, что в процессе производства решения, положения точек кривой, выраженной заданным уравнением, указывается индексами шкал. Диференциальные блоки механизма прибора составлены из червячных колес 2, расположенных в два горизонтальных ряда и несущих обоймы для вертикальных червячных колес 3, снабженных шестернями 15. Червячные колеса связаны между собою червяками 1, несущими на одном конце конические шестерни 8, соединяемые с шестернями 9 приводного вала 17. Подключение любого червяка / к валу 17 производится посредством подпружиненных ключей 7. На червячных колесах 2 верхнего ряда установлены индексы 5 области для отметок на главных шкалах 6. На маточных гайках 14 крайних червяков 12нижнего ряда установлены индексы 13контура, а отсчегг углов поворота червячных колес 5 производится посредством кремальер 4, соединяемых с шестернями 15 и несущими индексы 16 для отсчета по шкалам 11. Из рассмотрения фиг. 3 видно, что вращением червяков / можно перемещать колеса 2 и установить таким образом индексы 5 в любое первоначально заданное положение. Вращая червяки нижнего ряда, добиваются установки вертикальных колес «3 в нулевое положение, т. е. положение, соответствующее совпадению точек кривой n,k и n,k-}- 1 (см. фиг. 1). Момент наступления этого совпадения указывается индексами 16 на концах кремальер 4, устанавливаемыми на нули вспомогательных щкал У/. При внимательном рассмотрении нижней схемы (фиг. 2) нетрудно заметить, что м-омент совпадения всех точек обеих кривых, изображенных пунктирной и сплошной линиями, никогда не наступит, а будет при каждом очередном отрезке времени t происходить следующее: в какой-то момент перемещением вершин пунктирной ломаной кривой мы добьемся совпадения их со срединами прямых сплошной ломаной линии, что будет соответствовать приведению в нулевое положение кремальер 4 нижнего ряда и будет представлять собой операцию «подготовительную. В этот же момент все индексы кремальер 4 верхнего ряда будут смещены с нулей. Вращая червяки верхнего ряда и добиваясь установки на нуль индексов кремальер того же ряда, мы автоматически сместим в новое более высокое или низкое положение кремальеры 4 нижнего ряда. Этот момент и будет соответствовать новому положению заданной индексами -5 кривой, изменившейся за промежуток времени А t. В итоге решение сводится к следующему. Уравнение за. дается в виде кривой, первоначальный характер которой задается также и устанавливается индексами 5. Величина промежутка времени At вычисляется по формуле
., (Дл:), Я
Т т. е. толщина стенки Я, деленная на число слоев п. Поворачивая ключи 7 верхнего ряда, сцепляют конические П1естер и 8 червяков с шестернями 9 приводного вала 17. Поворотом ручки, надетой на трансмиссионный вал 17, вращают червяки / всего верхнего ряда и приводят кремальеры нижнего ряда на нули. Выключение каждой пары конических шестерен 9 происходит автоматически, что достигается следующим образом: на оси ключа 7 сидят защелки lOj которые силой пружины прижимаются к кремальерам 4. Зуб защелки может проскочить лишь через паз, устроенный в кремальере и расположенный так, что защелка проскакивает через него в момент установки ее на нуль вспомогательной шкалы 11.
Далее включаются ключи нижнего ряда и т. д. Нетрудно догадаться, что вращая весь ряд винтов мы, в отличие от графического способа последовательного построения, значительно экономим время, потребное на расчет, нб говоря уже о быстроте действий механизма в сравнении с вычерчиванием построений. Отсчет времени Л ведется по числу перемещений индексов 5.,
Задание может предусматривать любые пограничные условия, в том числе и переменный температурный режим по заданным графикам на обеих- границах. При таком задании графическое решение задачи становится трудным или часто просто практически невыполнимым; -го же самое можно сказать и об аналитических способах.
На предлагаемом приборе задача с ..переменными температурами на границах стенки решается так же просто, как это описано выше, с той лишь разницей, что через заданные промежутки времени Л t или п раз Л t следует, действуя крайними червяками 12, приводить их индексы 13 на заданную по графику температуру.
Соблюдение условий перехода на границах достигается введением поправочного коэфициента /С к температурам графика (или таблицы)
Д
2Дд:
А -Дл:
.-I
где
коэф. теплопроводности
о
коэф. температуропроводности.
Таким образом можно, отбросив так называемую по общепринятой терминологии, направляющую точку, придавать поверхностному слою тела температуру среды, исправленную на величину К.
Для решения задач, связанных с выделением или поглощением скрытого тепла, с чем, например, имеют дело при исследовании промерзания или оттаивания грунтов, при процессах, сопровождающих схватывание бетона и др., принцип решения остается прежним, т. е. при известном проценте насыщения грунта льдом известно и количество скрытого тепла, которое можно добавлять или отнимать. Последнее достигается перемещением индекса 5 путем вращения червяков 1 за специальные головки, вынесенные для этой цели- на наружную стенку прибора.
Предмет изобретения.
1. Прибор для решения уравнений
дт д I дт : „ ™Д ( с применением диференциальных зубчатых блоков для связи между отсчетными индексами контура и области, отличающийся тем, что, с целью производства решения уравнений методом Э. Шмидта, указанные диференциальные блоки составлены из расположенных в два ряда червячных колес 2, несущих обоймы для червячных колес 3 и связанных между собой червяками 1, причем на червячных колесах 2 верхнего ряда установлены индексы 5 области, в то


| название | год | авторы | номер документа |
|---|---|---|---|
| Прибор для решения дифференциальных уравнений | 1936 |
|
SU53526A1 |
| ПРИБОР ДЛЯ ГРАФИЧЕСКОГО ПОСТРОЕНИЯ ПРИ ПРОИЗВОДСТВЕ, НАПРИМЕР, ТЯГОВЫХ РАСЧЕТОВ КРИВЫХ ВИДА dv/dt=dl/dt=tgα | 1948 |
|
SU84067A1 |
| РЕГУЛИРУЕМЫЙ ВЕНТИЛЯТОР АППАРАТА ВОЗДУШНОГО ОХЛАЖДЕНИЯ | 2000 |
|
RU2183290C2 |
| СИСТЕМА КОРРЕКЦИИ ТРАЕКТОРИИ ДВИЖЕНИЯ АВТОМОБИЛЯ ПРИ БОКОВОМ ВЕТРОВОМ ВОЗМУЩЕНИИ | 2006 |
|
RU2320511C1 |
| Прибор для построения математических кривых | 1986 |
|
SU1362668A1 |
| ПРИБОР ДЛЯ ГРАФИЧЕСКОГО ПОСТРОЕНИЯ ПРИ ПРОИЗВОДСТВЕ ТЯГОВЫХ РАСЧЕТОВ КРИВЫХ ВИДА: DX/DT=TGα=Y/β | 1928 |
|
SU18559A1 |
| Прибор для прокладывания на карте пройденного пути | 1932 |
|
SU49853A1 |
| ТАХЕОГРАФ | 2004 |
|
RU2258905C1 |
| ПРИБОР ДЛЯ РАСЧЕТА ЖЕЛЕЗНОДОРОЖНЫХ КРИВЫХ | 1944 |
|
SU69645A1 |
| СПОСОБ КАРТОГРАФИЧЕСКОГО ОТОБРАЖЕНИЯ ДВУХМЕРНЫХ РАСПРЕДЕЛЕНИЙ, ЗАДАННЫХ В ЦИФРОВОЙ ФОРМЕ | 2011 |
|
RU2484427C1 |



Авторы
Даты
1940-01-01—Публикация
1939-05-31—Подача