Для определения тепловых характеристик (теплоёмкости, теплопроводности) различных естественных или искусственных материалов и вообще любых твёрдых или пластичных сред, изотропных в тепловом отношении, можно применить простой и удобный в обращении способ измерений - метод мгновенного источника тепла.
Согласно изобретению, измерение производят с помощью электрического нагревателя и электрического термометра, вводимых внутрь исследуемой среды. Выщеуказанные тепловые характеристики определяют по максимальному изменению во времени температуры среды, происходящему в результате распространения тепла от электронагревателя к электротермометру. Сущность изобретения поясняется прилагаемым чертежом и описанием.
В испытуемую среду вводят электрический нагревательный прибор (например, спираль константановой проволоки, намотанной на конец тонкого стержня из плохо проводящего тепло материала) и электрический термометр (термопара или термометр сопротивления). Обмотку нагревателя и
термометр для защиты от повреждений и влаги покрывают снаружи слоем электролитически осаждённой меди. Нагреватель и термометр помещают в среде на определённом расстоянии, причём глубина погружения от поверхности испытуемого материала должна быть не менее чем в четырепять раз больще разноса приборов. При включении электрического тока в течение краткого промежутка времени нагреватель распространяет дозированное количество тепла в окружающую среду. По термометру следят за изменением температуры. Последняя повыщается, достигает максимума и снова падает. Теоретический анализ явления распространения . тепла в среде для такого опыта показал, что максимальное повышение температуры вшах зависит только от количества тепла q, сообщённого источнику, объёмной теплоёмкости рс и расстояния г термометра от нагревателя. При этом функциональная связь между указанными параметрами выражена формулой 1.
qe
Вщах-
РсгЧ1-)
Измерением максимальной температуры вгпах. при известном количестве тепла q и расстоянии г можно определить объёмную теплоёмкость среды по формуле 2.
e-V2 q/Qmax - БД
Рс
где Bj-тепловая постоянная приборов.
Для определения температуропроводности а и теплопроводности К а рс необходимо измерить время tmax, в- теченив которого температура в точке г достигает максимума.
Коэфициент температуропроводности а, максимальное время tmax и расстояние г находятся в простой аналитической зависимости, определяемой по формуле (3):
а -6tmaxПриведенные выше формулы, которыми пользуются для-вычисления значений тепловых постоянных, являются следствиями исследования функции распределения температуры в в окрестности мгновенного источника тепла. Эта функция является частным решением уравнения теплопроводности Фурье 1 de a--dt( ДЛЯ следующих начальных и граничных условий: источник тепла локализован в исчезающе малом объёме среды, среда беспредельна, термически она изотропна: а const; температура в ней в момент сообщения тепла постоянна. Искомая функция распределения характеризует температуру 0, добавляющуюся к ранее существующей постоянной температуре. Для указанных начальных и граничных условий частным рещением уравнения 4 будет уравнение 5: PC (2а Y -1)3
где: рс - объёмная теплоёмкость среды,q - количество тепла, сообщённое исчезающе - малому объёму среды;
г - расстояние точки наблюдения температуры от источника тепла.
Температура 0 среды в точке, отстоящей на расстоянии г от источника тепла, достигает максимума через некоторое время после нагревания источника и снова падает. Нетрудно показать, что измерением времени, в течение которого температура в точке г достигает максимума tmax при известном расстоянии г, можно определять величину коэфициента температуропроводности исследуемой среды.
Для этого диференционированием уравнения 5 находят условие максимума функции распределения температуры (формула 6).
f2
(6)
tmax -
6a2 НО позволяет определять темпеатуропроводность а среды а -7 Заменим коэфициент температуопроводности я в уравнении 5 ыражением его через максимальое время tmax И расстояние г равнения (7): Рсг(-)(-.J Для максимальной температуры вшах в точке г, которая имеет место при t-tmax, уравнение (8) упрощается. q РеГ« (1-//0 шахГЭ(- г. )/2 Из уравнения 9 следует, что максимальная температура среды в каждой окрестной точке мгновенного источника тепла, локализованного в исчезагоще малом - объёме среды, есть простая функция количества тепла, сообщённого источнику q, расстояния точки г и объёмной теплоёмкости среды ре .
Такил5 образом исследование функции (5) распределения температуры в среде от мгновенного источника указало на чрезвычайно простой способ определения тепловых характеристик таковой. Определение тепловых характеристик среды при применении метода мгновенного источника сводится к измерению максимальной температуры в окрестной точке источника и регистрации времени, в течение которого температура достигает максимума. Следует указать на одну особенность в распределении температур, заключающуюся в том, что отношение значения максимальной температуры вшах в любой окрестной точке источника тепла к температуре источника Oj в момент достижения таковой равно постоянной величине
const.
«I
Исследование функции распределения температур мгновенного источника тепла указало на простой способ определения тепловых характеристик среды. Но все выводы, в том числе и решение основного уравнения теплопроводности, были получены при допущении идеальных условий опыта. Исследуемая среда была совершенно однородна. В области, где происходило распространение тепла, отсутствовали какие-либо посторонние тела с отличными от среды тепловыми свойствами. Источник тепла был локализован и в исчезающе малом объёме, а тепло ему сообщалось мгновенно.
Однако реальные условия далеки от тех допущений, которые сделаны в предыдущих выводах. Поэтому Для практической методики измерений следует внести исправления теоретических выводов.
Прежде всего необходимо экспериментально определить функцию
распределения температур/ которая является, отправным уравнением для всех дальнейших выводов.
В опытах изобретателя исследуемой средой служил мелкозернистый кварцевый песок-воздушно сухой и смоченный. В песок вставлялись нагреватель и электрический термометр - термопара, расстояние между ними измерялось. Через нагреватель пропускался в течение 4,23 сек. электрический ток и по зеркальному гальванометру через известные промежутки времени отсчитывалась температура, регистрируемая термопарой. Затем строились кривые зависимости температуры от времени, по которым определялась функция распределения температуры (уравнение 10). Отыскание функции облегчается тем, что известен вид функции для идеального случая.
(10)
После определения функции враспределения во времени выяснялось изменение температуры с изменением расстояния г между нагревателем и термометром и исследовалась зависимость между временем (в течение которого температура достигает максимума) и расстоянием. Эта зависимость наиболее близко удовлетворяет уравнению:
(r-Tj2,(11)
где Г(, - радиус нагревателя. Принимая с 1/6а, получаем
(г - го)д
(12)
6tmax
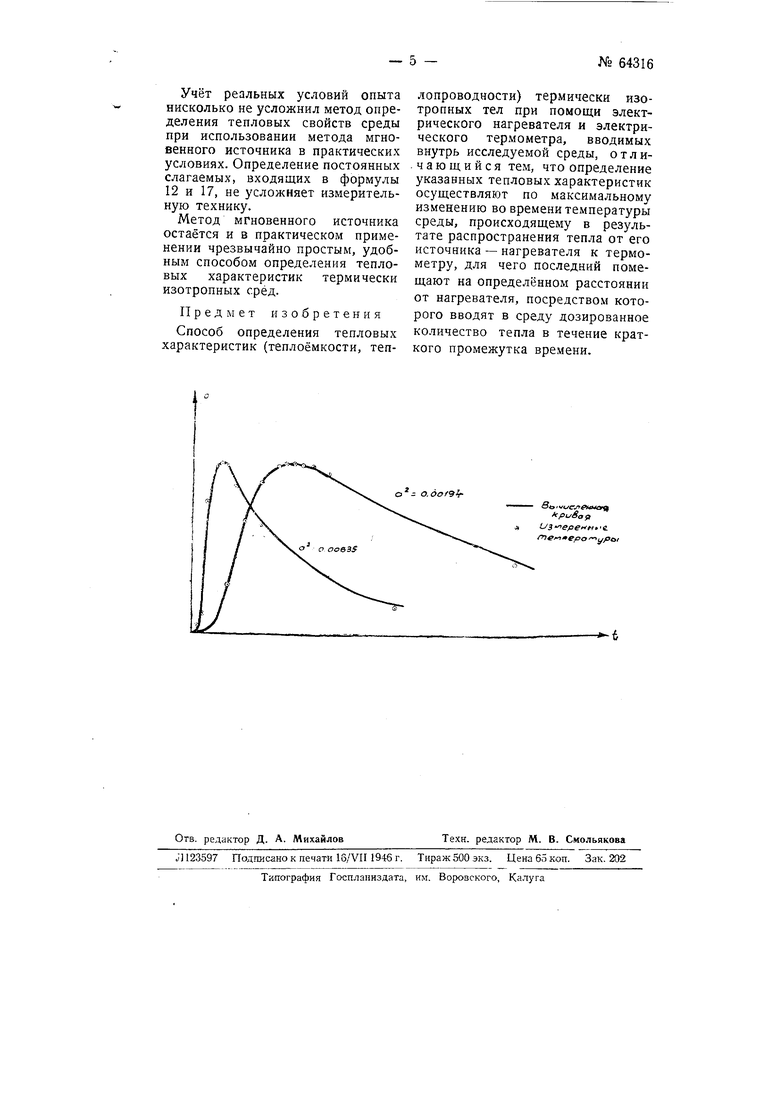
Пользуясь формулой (12), вычисляем значения коэфициента температуропроводности, которые имеют значения - для сухого песка а- 0,00194, для влажного и 0,00635.
Значение а- для сухого кварцевого песка, вычисленное по формуле (12), совпадает с табличными данными. В таблицах значение а даётся равным 0,0018 - 0,0023. Уравнение 12 может быть получено из уравнения 10, как условие максимума температуры. Поэтому из него можно определить множитель степени в уравнении 10 и оно может быть написано в законченном виде (13): (г - гЛ в Пользуясь полученными формулами, вычисляют значение температур для всего промежутка времени, в течение которого производят измерения. По вычисленным температурам составляют кривые, которые для конкретного случая, по опытам с песком, показаны на чертеже. Численные значения ординат кривых относительны, все значения температур кривых отнесены к максимальным температурам. Совпадение измеренных температур с вычисленными показывает что функция распределения температур, полученная в результате указанных экспериментов и последующей аналитической обработки измерений, удовлетворяет реальным условиям опыта. Уравнением 12 можно пользоваться для определения температуропроводности среды в практических измерениях. Найдём теперь уравнение для измерений теплоёмкости. Для этого составим уравнение теплового баланса системы (источник тепла-окружающая его среда) и преобразуем его в удобную для вычислений формулу: | /врс Напишем функцию распределения температуры в источнике тепла BI JlnlZ 01 e;r г„ ---; 6 ei е Расчленим уравнение 14 на составляющие (г - rj4 an q miCiOi -}- тгСгвз е+ ,)2 г4аЧ +j Ре 6164 p2d3, niiCj - теплоёмкость массы нагревателя, nijC, - теплоёмкость массы термометра, PC - объёмная теплоёмкость среды, г - расстояние от термометра до нагревателя. Го - радиус нагревателя. При составлении уравнения 1& считаем, что масса термометра мала и влиянием её на тепловое поле можно пренебречь, а теплопроводность материала нагревателя и термометра во много раз больще теплопроводности среды. Форму нагревателя принимаем шарообразной. (г - г J2 й ) 2--1Ч - «1 miCi + тоСо е + Рс(2а/).,(1б (г - Го)ч е, ве4a2t При измерениях определяем всегда максимальную температуру. После преобразований уравнение 16 примет вид (2)% (г-г„)(17 Таким образом в результате исследования явления распространения тепла в среде, в которую вводятся для производства измерений материальные приборы, мы пришли к формулам, совершенна аналогичным формулам, выведенным из предположения осуществимости идеальных условий опыта. Новые формулы содержат постоянные слагаемые В и Го. Только ими они отличаются от предыдущих формул идеального эксперимента.
Учёт реальных условий опыта нисколько не усложнил метод определения тепловых свойств среды при использовании метода мгновенного источника в практических условиях. Определение постоянных слагаемых, входящих в формулы 12 и 17, не усложняет измерительную технику.
Метод мгновенного источника остаётся и в практическом применении чрезвычайно простым, удобным способом определения тепловых характеристик термически изотропных сред.
Предмет изобретения
Способ определения тепловых характеристик (теплоёмкости, теплопроводности) термически изотропных тел при помощи электрического нагревателя и электрического термометра, вводимых внутрь исследуемой среды, отли. чающийся тем, что определение указанных тепловых характеристик осуществляют по максимальному изменению во времени температуры среды, происходящему в результате распространения тепла от его источника - нагревателя к термометру, для чего последний помещают на определённом расстоянии от нагревателя, посредством которого вводят в среду дозированное количество тепла в течение краткого промежутка времени.



| название | год | авторы | номер документа |
|---|---|---|---|
| Способ измерения теплофизических свойств теплоизоляционных материалов методом плоского импульсного источника теплоты с использованием большего объема экспериментальных данных | 2024 |
|
RU2826483C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТЕПЛОИЗОЛЯЦИОННЫХ МАТЕРИАЛОВ МЕТОДОМ ПЛОСКОГО ИМПУЛЬСНОГО ИСТОЧНИКА ТЕПЛОТЫ | 2015 |
|
RU2601234C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ АНИЗОТРОПНЫХ МАТЕРИАЛОВ МЕТОДОМ ЛИНЕЙНОГО ИМПУЛЬСНОГО ИСТОЧНИКА ТЕПЛОТЫ | 2015 |
|
RU2613194C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КИНЕТИЧЕСКИХ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТВЕРДЫХ МАТЕРИАЛОВ | 2018 |
|
RU2701775C1 |
| УСТРОЙСТВО ДЛЯ БЕСКОНТАКТНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТВЕРДЫХ ТЕЛ | 2018 |
|
RU2701881C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРОПРОВОДНОСТИ ОПТИЧЕСКИ ПРОЗРАЧНЫХ МАТЕРИАЛОВ | 2019 |
|
RU2725695C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТВЕРДЫХ МАТЕРИАЛОВ МЕТОДОМ ПЛОСКОГО МГНОВЕННОГО ИСТОЧНИКА ТЕПЛА | 2013 |
|
RU2534429C1 |
| Способ неразрушающего контроля комплекса теплофизических характеристик твердых строительных материалов и устройство для его осуществления | 2021 |
|
RU2767468C1 |
| Способ комплексного определения теплофизических свойств материалов | 1979 |
|
SU857826A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КИНЕТИЧЕСКИХ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ АНИЗОТРОПНЫХ КОМПОЗИТНЫХ МАТЕРИАЛОВ | 2020 |
|
RU2753620C1 |


3«у vc/C 4VMUr
ffpuSaf
L/з- еречие. сро 
Авторы
Даты
1945-01-01—Публикация
1943-10-25—Подача