(54) ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬ ОБРАТНОГО ГИПЕРБОЛИЧЕСКОГО
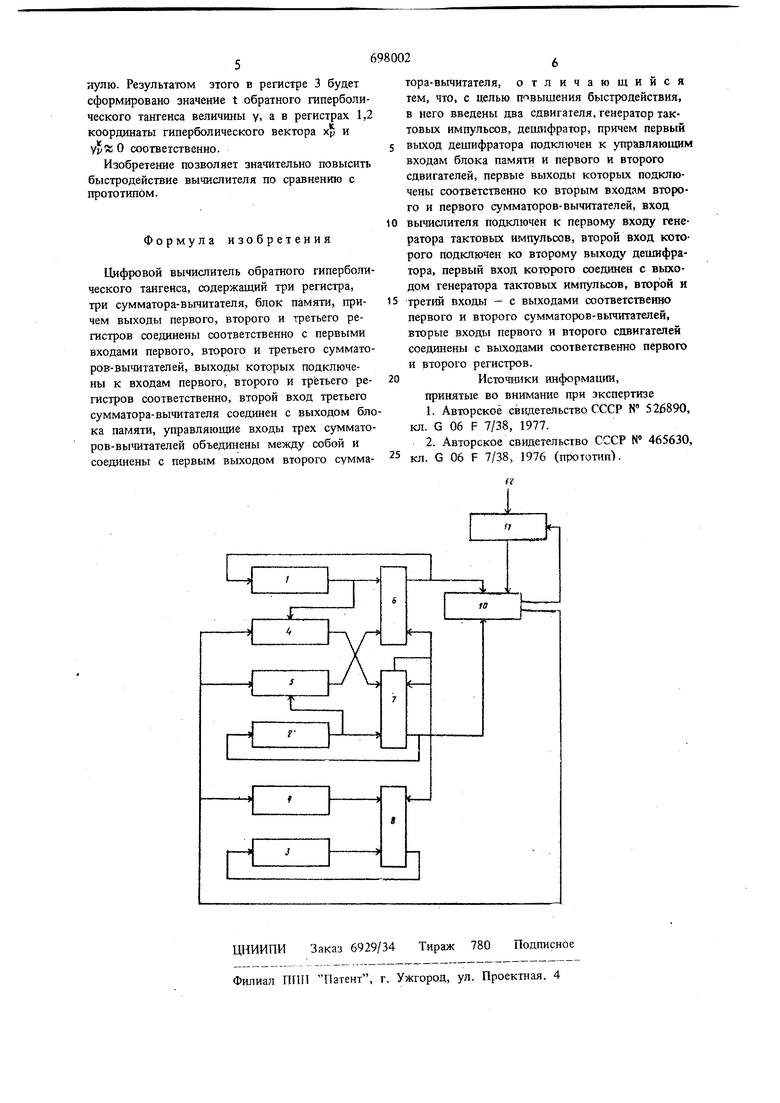
ТАНГЕНСА Цель изобретения - повышение быстродействия. Поставленная цель достигается тем, что в цифровой вычислитель обратного гиперболичес кого тангенса, содержащий три регистра, три сумматора-вь1читателя, блок памяти, причем выходы, первого, второго и третьего регистров соединены соответственно с первыми вхо дами первого, второго и третьего сумматоров вычитателей,выходы которых подключены к входам первого, второго и третьего регистров соответственно, второй вход третьего сумматора-вычитателя соединен с выходом блока памя ти, }шравляющие входы трех сумматоров-вычи тателей объединены между собой и соединены первым вьгходом второго сумматора-вычитателя, введены два сдвигателя,генератор тактовых импульсов, дещифратор, пртем первый выход дешифратора подключен к управляющим входам блока па1.1яти и первого и второго сдвигателей,. первые выходы которых подключены соответственно ко вторым входам второго и первого сумматоров-вычитателей, вход вычислителя подключен к первому входу генератора тактов 1х импульсов, второй вход которого подключен ко второму выходу дешифратора, первый вход которого соединен с выходом генератора тактовых импульсов, второй и третий выходы - с выходами соответствешю первого Ивторого сумматоров-вьчитателей, вторые входы первого и второго сдвигателей соед1ше1П)1 с выходами соответствешю первого и второго регистров. На чертеже показана блок-схема предлагаемого вычислигеля. Она содержит регистры (накопнтелып.1е) 1, 2, 3, сдвигатели (комбинационные) 4, 5, сумматоры-вычитатели 6, 7, 8, блок 9 памяти, дешифратор 10, генератор 11 тактовых импуль сов, вход 12 вычислителя. Алгоритм, по которому ведется итерационный процесс выделения обратного гиперболического тангенса, имеет вид + oraihZ i Начальные условия: Уо у, /i},Xo х|. где Xj;, Vj; - текущие значения гиперболичес кого вектора, 1 - номер итерации, причем множество значений этой величины является подмножеством переменной величины J, являющейся номером итерации в прототипе. ,- те конкретные значения j, для которых справедливо -г,а) oi ь .0 (3) г ё (0,1) - конституанта единицы, «j е (0,1) - коэффициент, зтсазывающий на присутствие или отсутствие доли координаты Ку в разности Кг; . i..(-vfo s 2- fv; i,,y „K K X};, У{; - конечные значения координат гиперболического вектора при вычислении предыдущего значения обратного гиперболического .тангенса от предыдущего аргумента у, t - вычисленное значение обратного гиперболического тангенса, Io sign7o оператор поворота вектора, определяющий направление итеращюнного процесса. Для обеспечения сходимости алгоритма, на тех итерациях, когда 3U + 1; U 1, 2,3 ... производится двойной поворот вектора на один и тот же угол а roth 2 . Вычислитель работает следующим образом. В регистре 1 значение , в регистре 3 значение tj, из предыдущих вычислений обратного гиперболического тангенса. В регистр 2 заносится значение у обратного гиперболического тангенса, которое необходимо вычислить. По высокому потенциалу, подаваемому на вход 12, генератор 11 начинает вьщавать1, серию тактовых импульсов на дещифратор 10. Значение у заносится в сумматор-вычитатель 7, после чего дешифратор 10 определяет нервое число , характеризующее наибольщую долю в разности у - Хр 7о при которой разность не становится противоположного знака в соответствии с выражениями (4) и (5). В результате определения jJi число х сдвигается на ju разрядов вправо и вычитается из То- Одновременно с этим формируется новое зйачение обратного гиперболического тангенса в соответствии с выражением (1). Одновременно с этим число у сдвигается вправо на i разрядов и заносится в сумматорвычитатель 6, в соответствии с выражением (1) После этого вновь формируется разность То - х - 2 7i. Далее определяется число р2 в соответствии с выражениями (2) -;f(5J и вычисляются новье значения координат гиперболического вектора. Процесс продолжается до тех пор, пока разность не станет равной

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления обратного гиперболического тангенса | 1987 |
|
SU1456952A1 |
| Устройство для вычисления тригонометрических функций | 1986 |
|
SU1332313A1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ МОДУЛЯ M-МЕРНОГО ВЕКТОРА | 1992 |
|
RU2029356C1 |
| Вычислительное устройство | 1986 |
|
SU1322270A1 |
| МАТРИЧНЫЙ СПЕЦПРОЦЕССОР | 1994 |
|
RU2079879C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ МОДУЛЯ M-МЕРНОГО ВЕКТОРА | 1995 |
|
RU2080650C1 |
| Вычислитель тригонометрических функций | 1978 |
|
SU746538A1 |
| Арифметическое устройство | 1978 |
|
SU780004A1 |
| Устройство для вычисления гиперболического тангенса | 1973 |
|
SU526890A1 |
| Устройство для вычисления тангенса | 1975 |
|
SU650073A1 |



Авторы
Даты
1979-11-15—Публикация
1978-06-07—Подача