Изобретение отмосится к цифровой вычислительной технике и может применяться при amnapBTiHotM вычислении элеме нта(рных функций, в частности, в специализированных двоич;ных цифровых вычислительных с фИ|К1СНрО1ва1Н.ной залятой.
Известно устройство для вычисления тригономет|рИЧеского тангенса, содержащее блок управлбния, выходы которого подключены к накопительным сдвигающим регистрам и блоку памяти, подключенному через таервый коммута1цио.н1ный логический элемент к входу nepiBOiro одноразрядного сумматора-вычитателя, приЧе1М выходы иакопительных регистров соединены с входами одноразрядных cyMiMaторо,в-1вычитателей, выходы которых соединены с входа.ми накопительных регистров, блок ап|ределвния цифры 1псавдочаст ного, входы которого этадключаны « знаковым выходам .первого л третьего накопительных регистров, блоки анализа сходимости, лодключеняые входами к раарядны.м выходам первого и третьего на-ко1П-ительных регистров, а выходами че|рез второй «оммутащионный логический элемент к блоку сброса, соединенному с блоком управления, вентиль, который второй нажапителъный регист р подключен .к блоку управления, причем уп|равляюш,ие входы вентиля, блока определения цифры псевдочастного и коммутационных логических элементов
подключены к общему выходу блока управления, а выходы второго и третьего накопительных регистров подключены соответственно к входам второго и третьего сдвигающих регистров, перекрестно соединенных с входами второго п третьего сумматоров-вычитателей.
Целью изобретения Я:вляется расширение класса рещаемых задач лутем вычисления функции гиперболического тангенса.
Это достигается тем, что в предлагаемое устройство Введены блок повторения итераций, вход которого подключен к блоку управления, и второй вентиль, через который выход блока повторения итераций подключен к блоку управления, а управляющий вход второго вентиля связан с общим выходом блока управления, причем выходы блока определения цифры псевдочастного подключены соответственно к объединенным входам первого и третьего и к входу второго сумматоров-вычитателей.
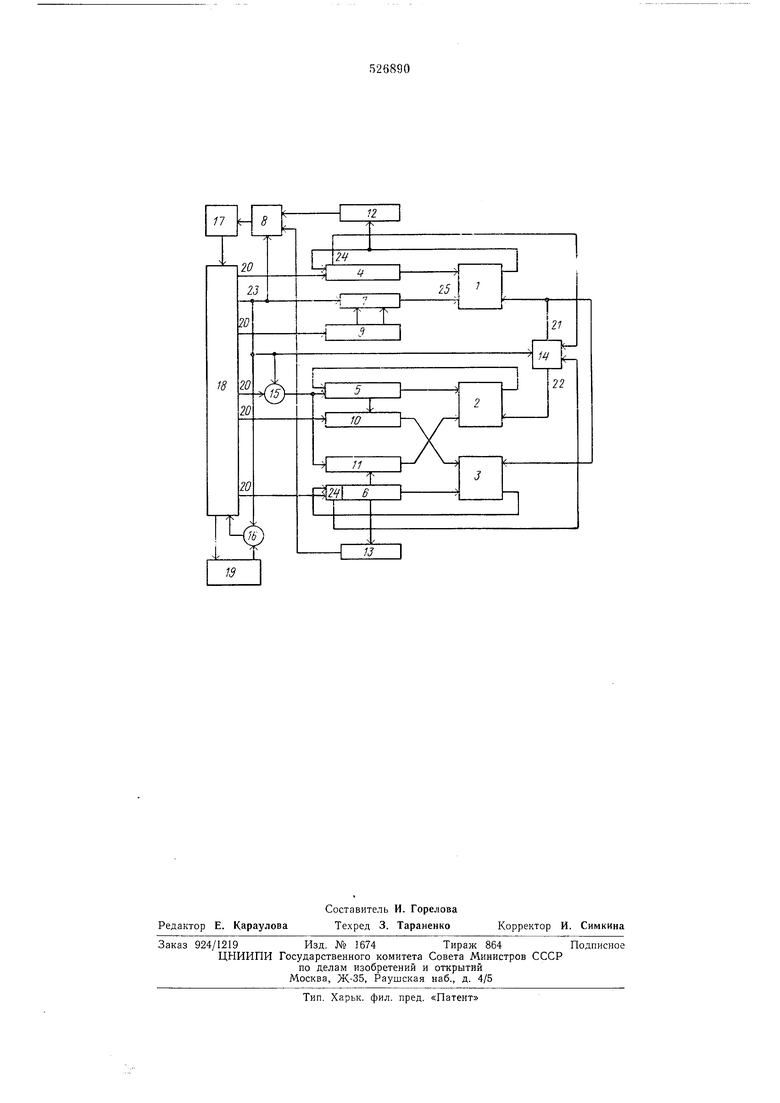
На чертеже показана блок-схема предлагаемого устройства.
Устройство содержит одноразрядные сумматоры-вычитатели /-3 комбинационного типа, накопительны е регистры 4-6, коммутационные логические элементы 7, 8, блок 9 памяти, выполненный в виде односторонней памяти с пораз,ряд|Ной выборкой двух слов одновременно, 1по:сл едав а тельные сдвигающие региспры 10, 11, блоки адализа сходимости 12, 13 (цифровые элел1енты сравнения с логичеокйм нулем), блок 14 о-п.ределелия цифры псевдочаст1ного, выполияющий функции коммутационного логического элемента, .вентили 15 и 16, блок сброса 17, блок 18 уп;ра.вления, блок 19 повт01рения итераций. Одноразрядный сум|Матор-(ВЫ1Ч|Итатель coiBMecTHO с накопительным регистром составляет рециркуляционную ячейку, из которых образуется параллельно-етоследавательная структура устройства. В бло1Ке 9 памяти хранятся константы arth ) и 2-ОЧ-1).
Константы выбираются одно1временно по одному адресу поразрядно каждым тактовыМ иМ|Нульсо1М, поступающим с выхода 20 блока 18 уйра.влеаия.
Выход 21 блока 14 выдает либо цифру нггвдочастного, либо ее инверсию, а выход 22 выдает цифру л-севдочастного.
:Вентили 15 и 16, коммутацио;нные логические элементы 7, 8 н блок 14 управляются сигналом с выхода 23 для перестройки свя32Й в структуре устройства, котарый вырабатывается элементом перестройки з блоке 18 упрааления.
Цикл вычисления гиперболического тангенса состоит из двух эта1пов.
На первом этапе вычисляются значения гиперболических си1нуса и косинуса, на втором этапе при помощи операции деления определяется тангенс задаииого аргумента t. В ocHOiBy вычислений положен принцип псевдоделения и поевдоумножения в итерационпом процессе. Псевдооперации выполняются при помощи элементарных операций сложения-.вычитания, сдвига и обращения к односторонней памяти.
Каждый этал вычисления состоит из итераций. В каждой итерации все разностные ракурсреншые соотнощения алгоритма рещаются параллельно. Каждое соотнощение вычисляется после|ДО(вательно за (п + т) тактов (где п - число разрядов аргумента; т- число дополнительных разрядов для ком,пенсации погрешности округления при сдвиге).
Вычисление гиперболических синуса и косинуса основано на итерационном алгоритме из разностных рекуррентных соотношений:
Z, f Zj+i Z; - qj arth 2---+) Z - 0 1 при Zj 0
Q/ signZ; i „ /-0,1,...,« 1 - 1 при Zj 0
X, - .- Xi+, Xi + ,y,2(/+ А-„ cht : A-,,,
л
У„ :: 0 Г;,, У , + F, Sht Г„,
В начальном состоянии в регистр 4 заносится значение аргумента t, в регистре 5 находится :нулевое значение, в
6 1иаходится значение, обратное коэффициенту изменения гиперболического вектора
п
К„- П() . Для выполнения условий
СХОДИМОСТИ на первом этапе необходимо повторять по два раза только итерации с номерами
Л-;:.4-3( Z 3,
I , -i- 1 1 i
где i l,2,..., р Ent 5n 4;5 -in3+ (
Таким об.разом, повторяются итерации с номерами Ai 4,13,40, 121,..., -%, 3/fe-М, . . . , т. е. / 1,2,3,4,4,5, ..., 13,13.. . и т. д. В повторяемых по два раза итерациях число сдвигов и очередное значение константы не из.ме«яются, а значение цифры псевдочастного q, (оператора поворота гиперболичеокого вектора) :на повторяемых итерациях может быть различным. Блок 19 повторения итераций
считает номера итераций и выдает сигнал разрешения перехода к следующему числу СДВИГ01В в константе.
На первом этапе имиульс управления с |выхэда 23 блока 18 открывает вентили 15 и
/ ко.ммутирует 1выход блока 12 на блок 17 п выход 24 знакового разряда регистра 4 на вход блока 14. На этом этапе первая рециркуляционная ячейка является псевдоделителем. ВтораяИ третья ячейки являются псевдоумножителями. На первом этапе иа выходах 21 и 22 блока 14 после каждой итерации появляется значение очередной цифры псевдочастного для следующей итерации. Коммутацио ННый логический элемент 7 проиускает иа
управляемый вход 25 сумматора-вычитателя / константу arth . В любой итерации с выходов 20 блока 18 управления поступает серия тактовых сдвигающих импульсов. Из содержимого регистра 4 вычитается при
qj + 1 очередное значение константы arth 2-(/ I). При Qj - 1 производится суммирование. По знаку результата операции псевдоделения находится очередная цифра qj. Содержимое накопительных, регистров 5 и 5
ячеек псевдоумножителей перекрестно суММИруется (либо вычитается при qj - 1) со сдвинутыми переадресов анными координатными составляющими ги|Пер болического зектора. Этот процесс можно интерпретировать
вращением этого вектора на сходящуюся последовательность гиперболических , узлов - констант. Полученный в 1каждой итерации результат последовательно, начиная с младших разрядов, заносится в освобождающиеся, при сдвиге старшие разряды накопительных регистров. После выполнения п + 1 итераций в регистре 4 находится нулевое значение, в регистре 5 - значение гиперболического синуса, а в регистре 6 - значение косинуса. .Однако для больщинства значений аргумента / итграционный процесс сходится на итерации, номер iKOTOpofj меньше п. При этом в регистре 4 получается нулевое значение. В результате срайне-ния содержания регистра 4 с логическим нулем в блоке анализа сходимости 12 с последнего выдается сигнал через элемеит 8 в бло,к сброса 17. Блок 18 прекращает выдавать та. имлульсы на следующей итерации, и процесс вычисления заканчивается. После остановки процесса вычисления первого этала элемент це.рестроЙ Ки структуры снимает сигнал уп1равления с выхода 23 блока 18. При этом вентили 15 и 16 заК|ры.ваются, элемент 8 соединяет выход блока 13 с входом блока 17, элемент 7 соединяет вход 25 сум матора-БЫчитателя 1 с выходом второй коичсталты (2-+) блока 9 -памяти, выход 24 знакового разряда регистра 6 соединяется с входОМ блока 14. На выходе 21 блока 14 в конце каждой итерации выдается инверсия очередной цифры лсевдочастного, на выходе 22 сигнал отсутсТ(Вует. Третья рециркуляционная ячейка служит псевдоделителем. Пе;р|вая ячейка служит псевдоумеожителем. Регистр 5 является пассивным и информативно связан только со сдигающим регистром 10. В регистре 5 и сдвигающем регистре // .продвижение информации отсутствует. Операция деления .в структуре устройства второго этапа реализует итерационный алгоритм из разностных рекуррэнтНых соотношений: Х,Х,„ А ,-+.,2-(/+) + 1 при . ... ,,:.SignA; { ,;..,1,...,Я у 7 - - -tht Zo 0 2;-f (7;2-( II -уL1. L . В начальном состоянии IB регистре 4 находится Нулевое значение гиперболического синуса, в регистре 6 - значение косинуса, полученные на первом этапе вычисления. После п + 1 итераций либо после срабатыБа Ния блока анализа сходимости /5 в накопительном регистре 6 находится нулевое значэние, в регистре 4 находится значение частио;-о, т. е. гиперооличеокин тангенс заданного аргумента. Максимальное 1В,ремя двухэтаиного цикла .вычисления гиперболического тангенса равно Г -. 2 ( 6л + 8) тактов. Формула изобретения Устройство для вычисления гиперболического тангенса, содержащее блок управления, выходы которого подключены к накопительным сдвигающим реги:страм и блоку памяти, подключенному через первый коммутационный логический элемент к входу первого одноразрядного сумматора-вычитателя, причем .выходы накопительных регистров соединены с вхОдаМи одноразряаных сум.маторов-вычитателей, выходы которых соединены с входами накопительных регистров, блок определения цифры псгздочастного, входы которого подключены к знаковым выходам первого п третьего на.копительных регистров, блоки анаЛ па сходимости, подключенные входами к разрядным выходам первого и третьего накопитзльных регистров, а выхода.м-и через второй коммутационный логический элемент к блоку.сброса, соединенному с блоком управления, вентиль, через который второй накопительный регистр подключен к блоку управления, причем управляющие входы вентиля, блока определения цифры псавдочастного и коммутационных логических элементов подключены к общему выходу блока управления, а выходы второго и третьего накопительных регистров подключены соответственно к входам второго и третьего сдвигающих регистров, перекрестно соединенных с входами второго и третьего сум.маторов-вычитателей, о тл и чающееся тем, что, с целью расширения класса решаемых задач путем вычисления функции гиперболического тангенса, оно содержит блок позторания итераций, вход которого подключен к блоку управления, и второй вентиль, через который выход блока повторен;я итераций подключен к блоку управления, управляющий вход второго вентиля связан с общим выходом блока управле:1ия, причем выходы блока определения цифры псевдочастного подключены соответственно к объед 1ненным входам первого и третьего и к входу второго сумматоровгвычитателей.


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления тригонометрического тангенса | 1973 |
|
SU537344A1 |
| Устройство для вычисления гиперболических синуса и косинуса | 1973 |
|
SU536490A1 |
| Устройство для вычисления логарифмической функции | 1973 |
|
SU541167A1 |
| Устройство для вычисления обратного гиперболического тангенса | 1973 |
|
SU465630A1 |
| Устройство для вычисления экспоненциальной функции | 1973 |
|
SU538366A1 |
| Устройство для формирования гиперболических функций | 1973 |
|
SU484522A1 |
| Двоичное устройство деления | 1975 |
|
SU541171A2 |
| Двоичное устройство деления | 1974 |
|
SU497585A1 |
| Устройство для вычисления тангенса | 1975 |
|
SU650073A1 |
| Устройство для вычисления кубического корня | 1973 |
|
SU516037A1 |


Авторы
Даты
1976-08-30—Публикация
1973-10-22—Подача