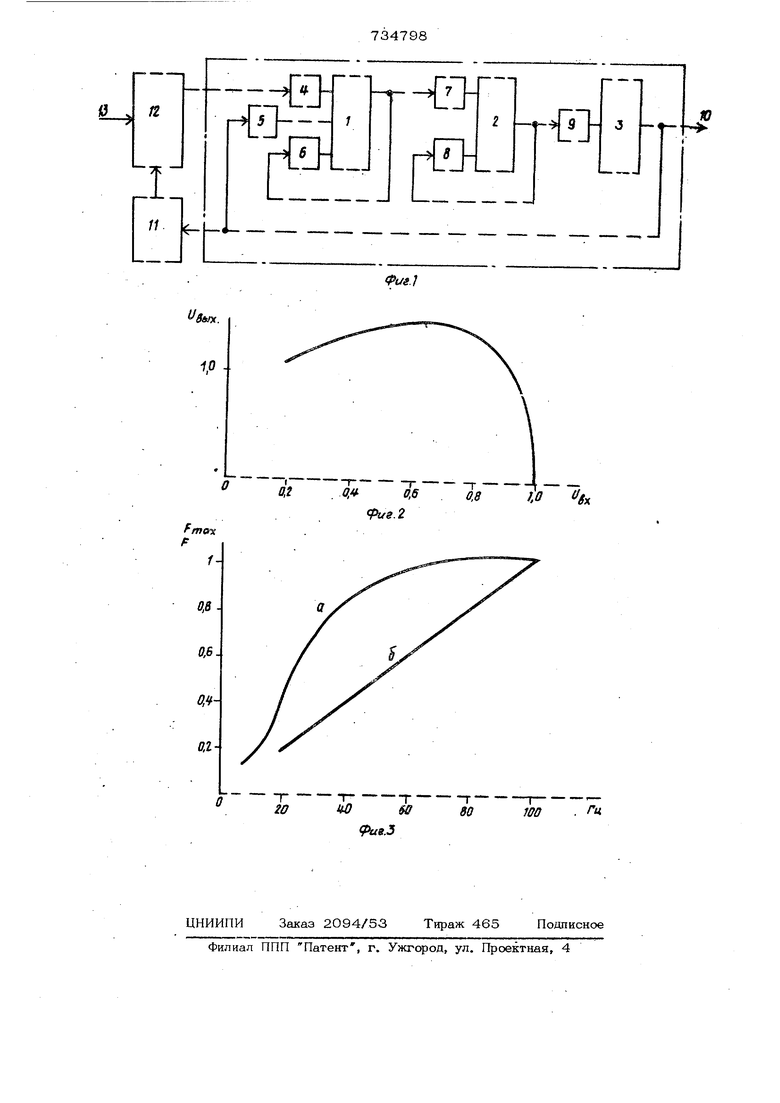
Изобретение относится к области моделирования биологических систем и может быть использовано при исследовании нейроннь1х механизмов управления мышечным сокращением. Известна модель мышцы, которая сод жйт п последовательно соединенных интеграторов с. сопротивлением в обратной связи l. Эта модель воспроизводит кривые одиночных и тетанкческих сокращений, изменяя напряжение на свое выходе в соответствии с частотой следования импульсов, поступающих по еевходу. Недостатком модели является то, что на ней не воспроизводится присущая реальной мыщце зависимость развития силы сокращения от частоты следования раздражающих импульсов, что ограничивает диапазон использования модели при исследовании .нейронных механизмов управления мыщечным сокращением. Целью изобретения является расщире- ние функциональных свойств модели и приближение их к свойствам реальной мышцы. Цель достигается тем, что в модель дополнительно введены блок умноже1шя и нелинейный элемент причем вход первого интегратора соединен с выходом блокф- умножения, один из входов которого является входом модели мышцы, а другой подключен к выходу нелинейного элемента, вход которого соединен 1 выходом последнего ( г -го) интегратора. На фиг. 1 изображена структурная схема модели мышцы; на фиг. 2 - характеристика нелинейного элемента; на фиг. 3 - зависимость напрях ения от частоты следования раздражающих импульсов для реальной мыщцы (Q ) и для модели (б)о . Модель мышцы содержит г последовательно соединенных, например, трех интеграторов 1, 2, 3, охваченных обратными связями через резисторы 4, 5, 6, 7, 8 и 9, величины сопротивлений ко-
торых определяют вид кривой оди14Очнаго сокращения. Выход последнего (п -го) шггегратора 3 является выходов: Ю модели мышцы и подключен к входу нелинейного элемента 11. Выход нелинейного элемента 11 связан с одним из входов блока 12 умножения, второй вход которого является входом 13 модели,а выход блока 12 умнол :ения подключен на , первого из цепрчки интегратора Модель работает следующим образом. В исходном состоянии напряжение на выходе модели равно нулю, на выходе нелинейного элемента имеется единичное напряжение, а напряжение на выходе блока умножения равно нулю, так кал на входе модели нет сигнала. При поступлении на вход модели импульсов их амплитуда умножается на напряжение, поступающее с выхода нелинейного эле-. мента, и преобразованные импульсы поступают на вход цепочки интеграторов На выходе модели напряжение изменяетс воспроизводя кривую мышечного сокращения. Изменением напряжения на выход модели мышцы изменяют напряжение на выходе нелинейного элемента и входной импульсный поток умножается на новую величину. При частоте следования импульсов на входе модели, меньшей частоты слияния одиночных сокращений, импульсы проходят через блок умножения умноженными на единицу. При увеличении частты следования импульсов одиночные сокращения на выходе модели сливаются сначала в зубчатый, а затем в гладкий тетанус, при этом входной импульсный поток умножается на величину, отлргчнуо на единицы и на интеградор поступа ют импульсы измененной а у-шли7уды, Таким образом коэффициент умножения входного импульсного потока определяется напряжением на выходе модели, котсрое в свою очередь зависит от амплитуды импульсов на выходе блока умножения Нелинейный элемент преобразует налряжение, поступающее на его вход в зависимость, представленную на фиг. 2,, Где ось абсцисс-напряжение, поступа о щее с выхода модели мышцы, а ось ор- дннат-напряжение на выходе нелинейного элемента, отражающее закон преобразования амплитуды входного импульсного потока для получения нелинейной зависимости развития напряжения на выходе модели от частоты следования импульсов на ее входе, которая предс-г-авлека на фиг. 3. Характеристика не- .кнекного элемента вычислена теоретически с помощью графического построе- шш и получена экспериментально на мо-
дели мышцы.
Постоянные времени интеграторов : коэффициенты в цепях обратной связи подбираются так, чтобы одиночная кривая сокращения по своим параметрам соответствовала кривой развития напряжения реальной мышцы. Параметры входного импульсного потока также соответствуют величинам, наблюдаемым в физиологическом эксперименте
Все это позволяет проводить эксперименты на модели в реальном, масшта-. бе времени и непосредственно сравнивать результаты биологического и модельного эксперимента. Модель мышцы с нелинейным характером преобразования частоты входного импульсного потока в силу сокращения позволяет расширить ,. диапазон применимости модели и переносить данные модельного эксперимента на биологический объект во всем диапазоне частот импульсных потоков, .поступающих на вход модели мышцы.
Фор, мулаизобретен и я
Модель мышцы, содержащая последовательно соединенных интеграторов, с сопротивлением в обратной связи, отличающаяся тем, что, с целью расшир91- ия функциональных свойств модели и приближения их к свойствам реапьной мышцы, в модель дополнительli,; bBSfie.tu,i блок умножения и нелинейный элемент, причем-вход первого интегратора соединен с выходом блока умножения, один из входов которого является входом модели мышцы, а другой подключен к выходу нелинейного элемента, вход которого соединен с выходом последнего (п -го) интегратора.
Источники информации,
принятые во внимание при экспертизе
1. Романов С. П.. Моделирование механизмов сигнального уровня управления мышечным сокращением, Физиологический журнал , СССР, 1974, N 10, с. 1508-1517.
t-f
/z
:L
11
r
-iilЮ
-Clh

| название | год | авторы | номер документа |
|---|---|---|---|
| Модель мышцы | 1982 |
|
SU1029761A1 |
| Модель мышцы | 1983 |
|
SU1164746A1 |
| Модель мышцы | 1978 |
|
SU765825A1 |
| Устройство для моделирования импульсных помех | 1982 |
|
SU1094037A1 |
| СПОСОБ БИОЭЛЕКТРИЧЕСКОГО УПРАВЛЕНИЯ СЕРВОПРИВОДАМИ ОРТОПЕДИЧЕСКИХ АППАРАТОВ | 1969 |
|
SU245990A1 |
| Устройство для моделирования электромагнитных процессов в асинхронных машинах | 1989 |
|
SU1681315A1 |
| Устройство для определения собственных параметров резонирующих тел | 1985 |
|
SU1319823A1 |
| СПОСОБ КОНТРОЛЯ ПАРАМЕТРОВ ЗВЕНЬЕВ СИСТЕМ УПРАВЛЕНИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1999 |
|
RU2156494C1 |
| Устройство для моделирования мышечного сокращения | 1987 |
|
SU1503832A1 |
| Модель рецептора-мышечного веретена | 1987 |
|
SU1511752A1 |

ивш.
i.O
(
0.2
0.8J.O Of
ff.0,6
9иг.2
fmpy
f
10,B. 0,6.
0,t0.
20
SOwo . f4
ZWe.J
Авторы
Даты
1980-05-15—Публикация
1978-01-10—Подача