(54) ВЕЮЯТНОСТНОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО ДЛЯ РЕШЕНИЯ ТРЕХМЕРНЫХ КРАЕВЫХ ЗАДАЧ



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для моделирования случайных блужданий | 1981 |
|
SU999063A1 |
| Устройство для задания конфигурации области | 1979 |
|
SU881774A2 |
| Устройство для моделирования -мерного изотропного вектора | 1978 |
|
SU752389A1 |
| Вероятностное устройство для решения краевых задач | 1982 |
|
SU1101838A1 |
| Устройство для моделирования диффузионных процессов | 1980 |
|
SU945873A1 |
| УСТРОЙСТВО для МОДЕЛИРОВАНИЯ МНОГОМЕРНЫХ ДИФФУЗИОННЫХ ПРОЦЕССОВ | 1973 |
|
SU377808A1 |
| Устройство для моделирования диффузионных процессов | 1978 |
|
SU769565A1 |
| Вероятностное устройство для решения уравнения Лапласа | 1981 |
|
SU1057956A1 |
| Вероятностное устройство для решения конечно-разностных уравнений | 1980 |
|
SU888119A1 |
| Способ и устройство определения координат источников радиоизлучения | 2018 |
|
RU2700767C1 |

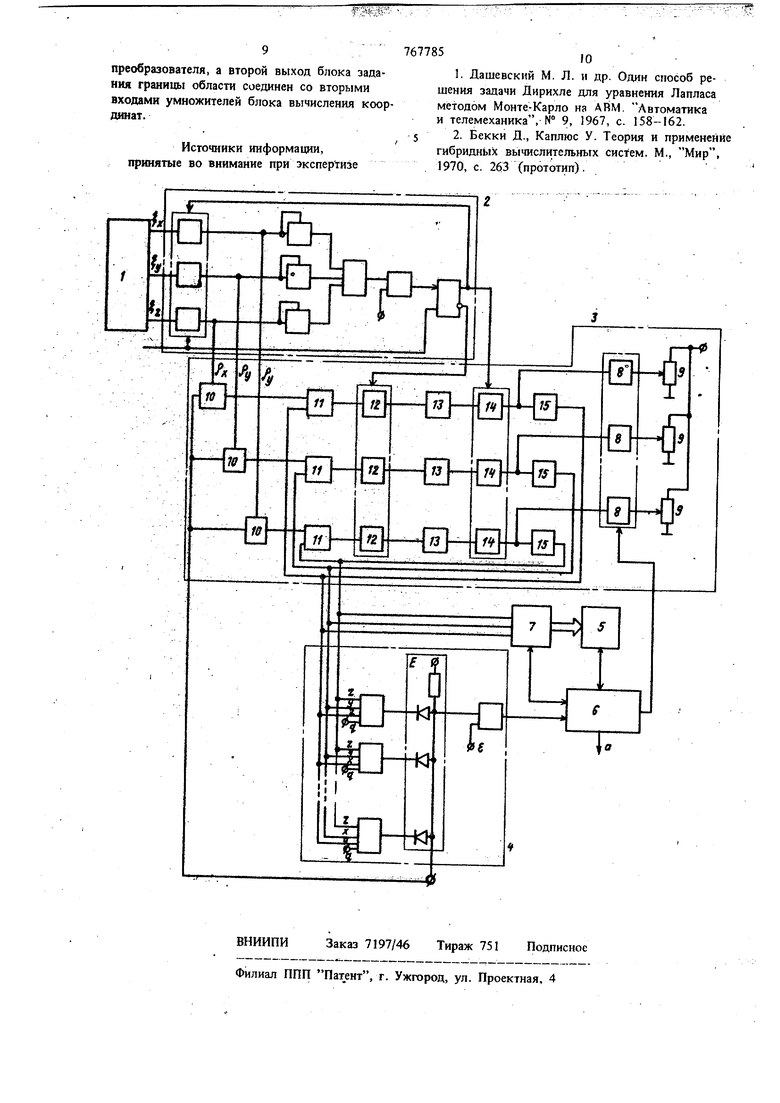
.:Л Изобретение ОТНОСИТСЯ к аналоговой вычислительной технике и предназначается Для применения как специализированное вычислительное устройство для решения трехмерных краевых задач материатической физики. Известно устройство, содержащее генераторы белого шума, интеграторы, блоки воспроизведения неданейных функций, блоки вычисления модуля разности координат блуждающей частицы и точки на границе, релейный элемент и схему контроля и управления 11. В процессе решения задачи производится непрерывное вычисление расстояния от блуждающей. внутри двумерной области частицы до точки, перемещающейся вдоль границы. К недостаткам этого устройства относятся су1цественное ограничение быстродействия, вы. зываемое необходимостью многократного полного обегания образующей точкой всей поверхности области, низкая точность задания конфигурации области, обусловленная наличием нелинейных функциональных преобразователей, практическая невозможность задания трехмерно области. Наиболее близким по техническому решений к изобретению является устройство, реализующее метод Монте-Карло 2. Известное устройство имеет следующие недостатки: невысокое быстродействие, обусловленное реализующимся в нем способом построения случайной траектории; низкую точность задания конфигурации области, обусловленную высокой погрейшостью реализации нелинейных функциональных зависимостей с помощью универсальных нелинейных функциональных преобразователей аналогового типа. Цель изобретения - повышение быстродействия и точности работы устройства. Для достижения этой цели, в устройство, содержащее генератор белого шума, блок задания гранипы области, первый выход которого соединен с первым входом блока уттравления, второй вход и первый выход которого соответственно связаны с управляющими выходом и входом аналого-цифрового преобразователя, информационные выходы которого соответственно соединены с ннформадаонными входами цифрового вычислителя, -выход и управляющии вход которого связаны соответственно с третьим входом и вторым выходом блока уп равления, дополнителы{о введены блок модели рования изотропного вектора (например, Ш) и блок вычисления координат, состоящий из трех каналов, каждый из которых содержит первый ключ, делитель напряжения, умножител и последовательно соединенные сумматор, второй ключ - первый аналоговый элемент памяти, третий ключ и второй аналоговый элемент памяти. Упра:вляющие входы второго и третьего ключей всех каналов блока вычислени координат подключены соответственно к первому и второму управляющим выходам блока моделирования изотропного вектора, выход каждого ключа блока вычисления координат соединен с информашоннйм входом соотйетствующего первого ключа, выход которого подключен .ко входу делителя напряжения сйоего канала. Управляющие входы первых ключей всех каналов связаны с третьим выходом блока управления. Выходы генератора белого щума соответственно соединены со входами блока моделирования изотропного вектора, информационные выходы которого , подклшчень соответственно к первьпи входам умножителей блока вычисления координат, а выход каждого умножителя - с первым входо соответствующего сумматора, второй вход-кото рого подключен к выходу Btopor;o аналогового элемента памяти своего канала, соединен с соответствующими входом задания границы области и информационным входом аналого-цифрового преобразователя. Второй выход блока задания гранищ 1 области соединён со вторьтми входами умножителей блока вычисления коорданат. На чертеже показана схема предлагаемого устройства., Устройствосодержит гедератор I белого шума, блок 2 моделиро1вания изотропного векTO}Ja, блок 3 вычисления координат, блок. 4 задания грани1да области, цифровой вьшислител 5, блок 6 управления и аналого-цифровой преобразователь 7. Блок вычисления координат содержит первые ключи 8, делители 9 напряжения, умножители 10, сумматоры 11, вторые ключи 12, первые аналоговь)е элементы 13 памяти, третьи ключи 14 и вторые аналоговые; элементь 15 памяти. Работа вероятностного вычислительного устройства для решения трехмерных краевых задач основана на применении метода ЙонтеКарло с использованием случайного процесса блуждания по сферам. Известно, что существующие методики получения рещения краевой задачи методом МонтеКарло сводятся, в главном, к организации серии случайных блужданий частицы внутри 54 области определения задачи, иачннаюишхся в той точке, где требуется определить значение функции, и заканчивающихся при определенных условиях на гранкце области. Характерной особенностью метода Монте-Карло является медленная сходимость получаемого рещения к истинному по мере увеличения числа испытаний, поэтому .на скорость рещения задачи существенно влияет время, затрачиваемое на построение одной случайной траектории. В описанном вероятностном вычислительном устройстве случайная траектория строится с помощью случайного процесса блуждания по сферам, при котором за один скачок траектория оказывается значительно ближе к границе, чем начальная точка, не. требуя долгого блуждания до пересечения с поверхностью сферы. Радиус сферы для достижения наибольщей скорости решения должен быть по возможности больще. Повторение этого процесса порождает последовательность случайных точек, сходящуюся к границе в несколько раз быстрее, чем обычные траектории, например типа броуновского движения или блуждания по рец1еткам.. Координаты точек этой последовательности вычисляются по формуле .,РС(.-Р - ( X ;, V;, 2. ) - координаты центра сферы на -j-M щаге; Я PXPiPz единичный изотропный . (равновероятный) сС(-,) - минимальное расстояние от центра сферы на ( j -1)-м шаге до границы области. Вероятностное решение трехмерной краевой задачи где и UCx.) - искомая функция; ,, z) - функция внутренних источников; Ч - SCX,3,Z - граничная функция в заданной трчке PQ-CXo. находится следующим образом. Строятся N независимых случайных траекторий, имеющих начало в точке РО и обрывающихся в -окрестности границы, Координаты точек траекторий вычисляются по формуле (1). Для каждой траектории вычисляется оценка |Ь ( решения по фор муле SH.Pj HVPMV составляющие оценки по внутренним точкам траектории, конкретный вид которых определяется видом функции и величиной коэффициента С; У (t) - составляющая оценки по последней точке траектории, принадлежа щей окрестности 6. границы; - случайное число шагов до выхода траектории в окрестность € границы. Решение в точке Ро находится усреднение j по числу N траекто полученных оценок рий UlPoV- ll Ъ. К--) Перед началом нахождения решения трехмерно краевой задачи в заданной точке Рд (Х о о выпуклой области, образованной совокупностью VV плоских граней, уравнения которых имею вид N j jz f -необходимо произвести задание конфигуращш области. Для этого уравнения (5) записываютс в нормализованной форме; . Задание конфигурации области производится установкой значений в блоке 4, Задание координат XQ.IO, о точки PQ, в которой требуется определить значение функции, производатся с помощью делителей 9 напряжения, на которых выставляются значения напряжений, соответствующие координатам На втором входе компаратора блока 4 задается напряжение , соответствующее шйри.не -окрестности границы. Вероятностное вычислительное устройство для решения трехмерных краевь1х задач работает следующим образом. По импульсу начала решения из блока 6 управления на управляющий вывод С блока 2 . моделирования изотропного вектора поступает управляющий импульс. В блоке 2 моделирования изотропного вектора начинается интегрирование некоррелированных сигналов белого ,N, z. При этом напряжения р,. вырабатываемые ни информационных вь1ходах блока моделирования избтропного вектора, соответствуют координатам частицы, совершающей броуновское движение из точки с координатами X -Z ОИзвестно, что броуновская траектория, начинающаяся вцентре сферы, с вероятностью, равной единице, выходит На поверхность этой сферы, и точка выхода имеет равномерное распределение. Это свойство используется для моделирования изотропного вектора р . В блоке 2 вырабатывается напряжение, пропорциональное квадрату расстояния блуждающей частицы от центра сферы 1 которое сравнивается с напряжением, представляющим квадрат радиуса сферьь Радиус сферы выбирается с тем расчетом, чтобы обеспечить достаточную для практики решения краевых задач точность моделирования изотропного вектора за минимальное время, пользуясь известнь1М соотношением, Ъ Одновременно с началом работы блока 2 моделирования изотропного вектора в цифровой вычислитель 5 через аналого-цифровой преобразователь 7 поступают напряжения с выходов вторых аналоговьнс элементов 15 памяти, представляющие координаты начальной точки, которые используюТсй дли вычисления значений оценки решения по формуле (3). Эти же напряжения поступают на вхо;аы блока 4 задания границы области. В момент времени, когда ч-р V на информационных выходах блока 2 фиксируются напряжения р,р р. соответствующие координатам изотропного вектора, а на выходах первых аналоговых элементов 13 памяти, отслеживающих напряжения на выходах сум- маторов П, устанавливаются напряжения, равныеГ- V o j o:
представляющие координаты следующей случайной точки Траектории, так как время работы блока 2 моделирования изотропного вектора всегда больше времени определения минимального расстояния X Pj) в блоке 4. Сигналы с управляющих выходов блока 4 задания конфигурации области закрывают вторые ключи 12 и открывают третьи ключи 14, благодаря чему напряжения Х, из первых аналоговых элементов 13 памяти, переписываются во вторые аналоговые элементы 15 памяти,хранившие напряжения . (Соответствующие координатам начальной точки. Время работы аналого-цифрового преобразователя 7 меньше времени работы блока 2 моделирования изотрр1шого вектора, поэтому к моменту выдачи сигналов с )Т1равляющих выходов блок 2 координаты начальной точки РО будут уже находиться в памяти цифрового вычислителя 5, который находит значение составляюш;ей (РО) оценки А решения по первой траектории. На этом первый шаг нахождения оценки р решения задачи заканчивается.
В следующий момент времени из блока 6 управления на управляющий вход сС блока
, моделирования изотропного вектора поступает управляющий импульс, по которому начинается моделирование следующего изотропного ветктора. Ключи остаются закрытыми, а в остальных блоках повторяются те же процессы что и на предь1дущем шаге в той же последовательности. После выполнения второго шага
ЩпЬлмяется третий И так до тех пор, пока напряжение на выходе схемы выделения минимума блока 4 задания границы .области не станет меньше или равно напряжению 6 , что соответствует выходу случайной траёктсфйй в 6 -окрестность границы. В этот момент на вь1ходе блока 4 возникает сигнал, ггbctyпaн)щий в блок 6 управления, оповещая об обрыве траектории. В цифровом вычислителе 5 находится оценка jb-i решения по первой траектории (по формуле (3))j а в память заносится
..единица; / ; . : : . - / - ;
В следующий момент времени начинаетс я . нахождение составляющих оценки а решения задачи по второй случайной траектория. Из
, блока 6 управления йа управляющий вывод 01 блока 2 модёлировання изотропного вектора и на ключи 8 пЬступают управляющие импульсы, и все повторяется аналогично преды.дупдему. .. .
Когда число траекторий N достигает задан; ного значения, 1{ифровой вычислитель 5 определяет значение искомой функции по формуле (4) и решение прекращается.
Таким образом вероятностное вычислительное устройство для рещеиия трехмерньис краевых задач, выпо;1ненное в соответствии с .
изобретением, обладает более высокими быстродействием и точностью по сравнению с известными специализированными вероятностными вычислительными устройствами.
Повышение быстродействия достигнуто за счет введения блока моделирования изотропного вектора и блока вычисления координат, за счет чего реализован более быстрый и точный способ построения случайной траектории.
Формула изобретения
Вероятностное вычислительное устройство для решения трехмерных краевых задач, содержащее генератор белого шума, блок за. Дания границы области, первый выход которого соединен с первым входом блока управления, второй вход и первый выход которого соответственно соединены с управляющими выходом и входом аналого-цифрового преобразователя, информационные выходы которого с оответственно соединены с информационными входами цифровогс вычислителя, выход и управляющий вход которого свйзаны соответственно с третьим входом И вторым выходом блока управления, отличающееся тем, что, с целью повышения быстродействия и точности, В него дополнительно вв.едены блок моделирования изотропного вектора и блок вычисления координат, состоящий из трех каналов, каждый из которых содержит первый ключ, делитель напря кения, умножитель и последовательно соединенные сумматор, второй ключ первый аналоговый элемейт памяти, третий ключ и второй аналоговый элемент памяти,, управляющие входы второго и третьего к.шочей всех каналов блока вычисления координат подключены соответственно к первому и второму управляющим выходам блока моделирования изотропного вектора, выход каждого третьего ключа блока вычисления координат соединен с информаплонным входом Соответствующего первого ключа, выход которого подключен ко входу делителя напряжения своего канала, управляющие входы первых ключей всех каналов соединены с третьим выходом блока управления, причем Выходы генератора белого шума соответственно соединены со входами блока моделирования изотропного вектора, информационные выходы которого соединены соответственно с первыми входалвд умножителей блока вычисления координат, выХод каждого умножителя соединен с первым входом соответствующего сумматора, второй вход которого подключен к выходу второго аналогового элемента памяти своего канала, соединен с соот; вётствующими входом задания границы области и информационным входом аналого-цифрового
Авторы
Даты
1980-09-30—Публикация
1978-11-13—Подача