(54) УСТРОЙСТВО ДЛЯ РЕШЕНИЯ СИСТЕМ
ЛИНЕЙНЫХ УРАВНЕНИЙ С РАЗРЕЖЕННОЙ МАТРИЦЕЙ
с первым входом арифметического блока, первый выход которого подключен к третьим входам решающих блоков матрицы, арифметический блок соединен двухсторонними связями с блоком постоянной памяти и с блоком управления, установочный выход которого соединен с первым и вторым входами программного блока, третий и четвертый входы которого соединены с первым выходом блока ввода коэффициентов, второй, третий и четвертый выходы которого подключены соответственно к первому входу блока опетивной памяти, входу запуска .блока управления и второму входу, арифметического блока, выход блока оперативной памяти соединен с третьим входом арифметического блока, выход которог подключен к первому входу блока вывода, первый и втопой выходы программного блока соединены соответственно со вторым и третьим входами блока вывода и первым и вторым входами блока сравнения, выход которого подключен к сигнальному входу блока управления, выход записи которого соединен со входом блока оперативной памяти, группа выходов программного блока соединена с управляющими входами решающих блоков матрицы, содержит счетчик синхронизации, причем первый выход счетчика синхронизации подключен к четвертому входу арифметического блока, а второй выход - к синхронизирующему входу блока управления.
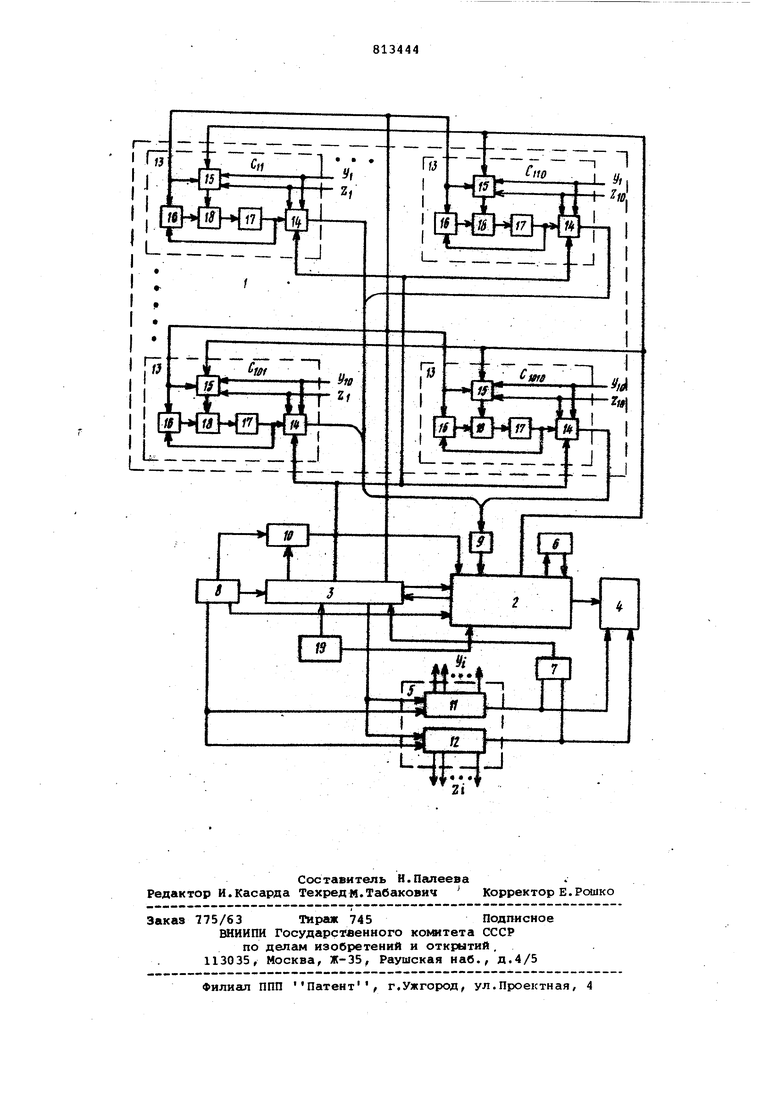
На чертеже представлена блок-схем устройства.
Устройство содержит матрицу 1 решающих блоков, арифметический блок 2 блок 3 управления, блок 4 вывода, программный блок 5, блок 6 -постоянной памяти, блок 7 сравнения, блок 8 в6да коэффициентов,элемент ИЛИ 9 ,блок 10 оперативной памяти, счетчик 11 строк, счетчик 12 столбцов, решающий блок 13, элементы И 14, 15, элемент НЕ 16, регистр 17, элемент ИЛИ 18, счетчик 19 синхронизации,
В устройстве реализуется метод решения систем линейных уравнений с разреженной матрицой по частям. В общем случае система уравнений представляется в кратной Форме:
H.,(1)
где Н - неособенная матрица коэффициентов системы; X - вектор столбца неизвестных
величин;
Q - известный вектор правых частей .
Используя операцию развертывания, исходную систему порядка п можно привести к виду
о
(2)
Q
где Vfe - квадратная подматрица связи; Н - блочно-диагональная матрица исходной системз, содержащая N подматриц, размерностью t; Qf(i - прямоугольные подматрицы
после операции развертывания, количество которых равно N, размерностью t; Хр - вектор дополнительно введенных переменных;
- порядок блочных матриц после разбиения системы. Такая система решается по частям согласно ее разбиения на прямоугольные блоки.
Согласно алгоритма определяется матричное произведение В
-; .(3)
где Hi - обратная матрица подматри0 дЦЬ1 Н,- .
Определяем К,.
(4)
Далее определяется вектор Q
QC .zer HV- Q- (5) Находится неизвестный вектор связи Хс. .
(6)
Далее определяются подвекторы о, выраженные через вектор связи х, которые необходимы для окончательного решения по частям система уравнений
Qj Qi-0i-Xc(7)
Далее решение сводится к определению неизвестных подвекторов X,,X, 5 Xj , ..., X,, в виде матричного произведения
(8)
Полученные подвекторы Xf состоят из неизвестных численных величин Q вида
t
Hi;
X,
X
х., i х
Устройство работает следующим образом.
Счетчик 19 сиихронизёщии вырабатывает синхрюнизирующие импульсы, которые поступают в блок 3 упр авления и арифметический блок 2 и стробируют обрабатываемую информацию. Информация в регистрах арифметического блока 2 обрабатывается при помощи микрюкомаид, синхронизированных во времени счетчиком 19 синхронизации и поступающих с блока 3 управления. Счетчик 19 синхронизации синхронизирует информацию так, что регистр 17 каждого решающего блока 13 матрицы 1 условно разбит на три
регистра Ct, б с по времени синхронизации, которое задает счетчик 19 синхронизации. Таким образом, в определенное время в одном регистре 17 можно хранить три числа в условно обозначенных регистрах CL, 0« с,
Следовательно, одна матрица 1 условно разбивается на три матрицы Ма Mb, MC по времени синхронизации, определяемого счетчиком 19 синхронизации. Регистр 17 каждого решающего блока представляет собой сдвиговый регистр с обратной связью через элемент НЕ 16 и элемент ИЛИ 1Ь. Один оборот регистра 17 равен времени счета счетчика синхронизации,
С помощью блока 8 ввода коэффициентов набираются построчно коэффициент за коэффициентом подматрицы Н, При наборе 1-ой строки счетчик 11 строк программного блока 5 устанавливается в 1-ое состояние,а при наборе первого коэффициента h счетчик 12 столбцов программного устройства 5 устанавливается в 1-ое состояние, по сигналам, поступающим с блока 8 ввода коэффициентов. В этот момент счетчик строк 11 и счетчик столбцов 12 соответственно вырабатывают сигналы у и поступающие на входы второго элемента И 15 решающего блока 13 матрицы 1. Таким образом произошел выбор решающего блока С . В эту ячейку С-ц матрицы Mq заносится преобразованный на арифметическом блоке 2 коэффициент: h , При вводе коэффициента h запускается блок 3 управления, который работает по микроп ограмме преобразования коэффициентов подматрицы H по методу разложения матрицы на треугольные множители с записью этих коэффициентов в виде таблицы множителей в матрицу Mq. Коэффициент h заносится в апифметический блок 3, преобразуется и пересылается в ячейку С раиающего блока матрицы MO через элемент И 15, на который поступает микрокоманда с блока 3 управления. При совпадении сигналов у , 2 и микрокоманды происходит запись элемента h через элемент И 15, элемент ИЛИ 1В в регистр 170, в котором h хранится при помсяди циклической перезаписи чрез элемент НЕ 16 и элемент ИЛИ 18,
Ввод последующих коэффициентов подматрицы Н осуществляется аналогично, при этом счетчик 11 строк и счетчик 12 столбцов вырабатывают соответствукицие координатные сигналы у и Zj, которые выбирают соответствующие решающие блоки Cjj матрицы 1, Блок 7 сравнения сравнивает содержимое счетчиков строк и столбцов. Если эти счетчики равны, идет обработка диагональных элементов подматрицы Н,, . Если содержимое счетчика 11 строк меньше содержимого счетчика 12 столбцов, то ведется обработка коэффициентов вьаие главно диагонали подматрицы. Если содержимое счетчика 11 строк больше содержимого счетчика 12 столбцов, то обрабатываются коэффициенты, расположенные ниже главной диагонали подматрицы. Результаты сравнения передаются в блок 3 управления, который вырабатывает определенные (крокоманды, необходимые для обработки коэффициентов в -арифметическом блоке 2. Арифметический блок 2 выполняет операции сложения, вычитания, умножения, деления, накопления и алгебраического сложения, которые обесoпечивают весь вычислительный процесс. Микропрограмма, выполнякхцие данные операции, служат, как микроподпрограммы для решения системы линейных уравнений.
5
После ввода всех коэффициентов подматрицы Hi, нажимается, например, клавиша И, По этой команде запускается блок 3 управления, который работает по микропрограмме обращения
0 подматрицы H-J в обратную подматрицу Н . Цля обращения псдмат1жцы используется метод прямых решений с использованием разложения матрицы на треугольные множители. Обращение матрицы Н заключается в том, что из по5лученной матрицы коэффициентов матрицы 1 Mq выбирается треугольная матрица, которая поэлементно пересылается в матрицу 1 М через элемент ИЛИ 9 и арифметический блок 2.
0
Далее производится матричная операция умножения матрицы М на матричные треугольные множители матрицы MQ, Результирующая матрица накапливается в матрице М, При ум5ножении матриц коэффициенты вызываются в арифметический блок 2 через элемент ИЛИ 9 и происходит их умножение с алгебраическим накоплением.
Обратная матрица Н накаплива0ется в матрице 1 м. Далее на блоке В ввода коэффициентов нажимается клавиша в, это означает, что в матрицу 1 Mq вводятся коэффициенты подматри1Ц1 е . Нажимается клавиша множить и происходит операция мат5ричного умножения в , на Н .матричное произведение Н хранится в 1 MQ
Нажимается клавиша Q и осуществляется ввод Q - часть известного
0 вектора, которая соответствует части матрицы Н. Ввод Q поэлементно осуществляется в блок 10 оперативной Помяти по микрокоманде с блока 3 управления. После этрго нажимает5ся клавиша УМНОЖИТЬ и происходит матричное умножение матрицы MQ на -известный вектор Q,, Получим произведение 6-1 Н Q по выражению (5) в виде вектора размерностью Q,
0 Полученный вектор для накопления засылается в блок б постоянной памяти, где будет накапливаться вектор QC, по выражению (5).
По нажатию клавиши Ф запускается
5 блок 3 управления и происходит занесение коэффициентов подматрицы в матрицу 1 М через арифметичэский блок 2 с блока 8 ввода коэффициентов. После чего нажимается клавиша множить и происходит операция матричного умножения матриды MO на матрицы М. В результате получается матричное произведение 8 Н 0 по выражению (3) , которое-хранится в матрице MQ. Подматрица связи W - единичная матрица и она находится в матрице MC , Определяется KC опергидией матричного сложения по выражению (4) KC ,Wc- . Результат величины KC накапливается ,в матрице MC, . Далее осуществляется ввод второй части исходной матрицы Н, т.е. осуществляется последовательньй ввод подматриц Hj,® Qi и 0а и про-) делываются все матричные операции с этими подматрицами тем же способом. Последовательность нажатий клавиш остается без изменения. После выполнения всех операций в блоке б постоянной памяти накапливается выражение 5 , а в матрице М накапливается результат Kj. выражения (4) . Осуществляя ввоя последующих частей исходной матрицы Н по подмат рицам Н , ® г Qj и последней части Н„, в„, Q и 0ц и проделав матричные операции, получаем окон-. чательный результат Q и Кс по выражениям (5) и {-4), которые накап.ливаются соответственно в блоке б постоянной памяти и в матрице Мс. Для определения неизвестного век тора связи Хс по выражению 6 нажимается клавиша Х,, по которой происходит обращение К в обратную мат рицу К по методу npHhffiix решений с использованием разложения матрицы на треугольные множители. Обращение идет тем же способом, когда находилась обратная матрица Н . Далее происходит матричная операция умножения .Ма-0«.Для этого поэлеме тно на арифметический блок 2 вызыва ются QC из блока б постоянной памяти и KC из матрицы 1 MQ через Элемент ИЛИ 9. Результат вектора Хс, на капливается в блоке б постоянной па мяти . После получения вектора X с. можно найри неизвестный вектор X по частя Для этого нажимается клавиша Ф по которой запускается блок 3 управления и происходит занесение коэффици ентов подматрицы Ф в матрицу 1 М. По нажатию клавиши |Умножить происходит матричное умножение Ф X с, выражения (7) на арифметическом блоке 2 с вызовом поэлементно Ф и Хс из матрицы М(, и блока б постоянной памяти. Результат накапливается в бло ке 6 постоянной памяти. При нажатии клавиши Q осуществляется ввод Q - части известного вектора в блок 10 оперативной памяти. После ввода происходит векторное вычитание по выражению (7) Вычитание происходит в арифметическом блоке с вызойом элементов вектора Q из блока 10 оперативной памяти и вектора Ф, х из блока 6 памяти. Результат засылается в блок б постоянной памяти. Осуществляется ввод подматрицы Н в-матрицу MO. Находится обратная матрица Н , которая записывается в матрицу Mq. После этого нажимается клавиша „УМНОЖИТЬ, по которой происходит матричная операция умноженияк, матрицы 1 Ма на блок б постоянной памяти. На арифметическом блоке 2 выполняется выражение (8) Q Результат вектора Х .. . | ХЛ записывается в блок & постоянной памяти. Численное значение найденного Вектора Х передается в блок 4 вывода и индикации. Этот результат может вь печатываТься в устройстве вывода на бумажной ленте или высвечиваться на цифровом табло. Осуществляется ввод последующих частей матрицы Н по подматрицам (8i, Qj и Н{ до последней части 0, Эм , Нц . Произведя все матричные операции и вычисления по выражениям (7) и (8) получим все численные значения вектора X t х„..., Полученные результаты решения исходной систегФ уравнения по частям печатаются на бумажной ленте или высвечиваются на цифровом табло. Эффективность использования предлагаемого устройства и метода решения системы линейных уравнений с разреженной матрицей проявляется в экономичном использовании аппаратурных затрат. Уменьшается количество связей между блоками и количество Сс1мих блоков. Упрощается методика микропрограммирования при разработке устройства и само устройство, которое дает возможность решить практически любую больш о систему линейных уравнений с разреженной матрицей в. малом аппаратурном объеме. Формула изобретения Устройство для решения систем линейных уравнений с разреженной матрицей, содержащее матрицу решающих блоков, арифметический блок, блок управления,, блок вывода, программный блок, блок постоянной памяти, блок оперативной памяти, блок сравнения, блок ввода коэффициентов, элемент
ИЛИ, причем первый и второй разрешающие выходы блока управления соединены соответственно с первыиш и вторыми входами решающих блоков матрицы, выходы которых соединены через элемент ИШ с, первым входом арифметического блока, первый выход которого подключен к третьим входам решающих блоков матрицы, арифметический блок соединен двухсторон- ними св;язями с блоком постоянной памяти и с 6ЛО.КОМ управления, установочный выход которого соединен с первым и вторым входами программного блока, третий и четвертый KOTOpoio соединены с первым выходом блока ввода коэффициентов, второй, третий и четвертый выходы которого подключены соответственно к первому входу блока оперативной памяти, входу запуска блока управления и второму входу арифметического блока, выход блока оперативной памяти соединен с третьим входом арифметического блока, выход которого подключен к первому входу блока вывода, первый и второй выкоды программного блока соединены соответственно со {вторьм и третьим вхоДс1ми блока вывода и первым и вторам входами блока сравнения, выход коf торого подключен к сигнальному вхо ду блока управления, выход записи которого соединен со вторам входом блока оперативной памяти, группа выходов nporpaMNMoro блока соединена
с управляюошми входами решающих блоков матрицы, отличающеес я тем, что, с целью упрощения устройства, оно содержит счетчик синхронизации, причем первый выход счетчика синхронизащси подключен к четвертому входу арифметического блока, а второй выход - к синхронизирующему входу блока управления.
Источники информации, принятые во внимание при экспертизе
0 1. Авторское свидетельство СССР № 294144, кл. G 06 F 15/32, 1971.
2. Авторское свидетельство СССР по заявке 2531210/18-24, кл. G 06 F 15/32, 1977 прототип).
llfr
L-.-nrn-l




| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровое устройство для решения системы линейных уравнений | 1977 |
|
SU714409A1 |
| Цифровое устройство для решения системы линейных уравнений | 1976 |
|
SU624234A1 |
| Электронная клавишная вычислительная машина | 1978 |
|
SU785869A1 |
| Устройство для вычисления двумерного быстрого преобразования Фурье | 1986 |
|
SU1408442A1 |
| СПОСОБ ПЕРЕДАЧИ ДИСКРЕТНОГО СООБЩЕНИЯ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2179365C1 |
| СПОСОБ ПЕРЕДАЧИ ДИСКРЕТНОГО СООБЩЕНИЯ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2179366C1 |
| УСТРОЙСТВО ДЛЯ ЗАПИСИ И ОТОБРАЖЕНИЯ ИНФОРМАЦИИ | 1992 |
|
RU2101781C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДАННЫХ | 2005 |
|
RU2370886C2 |
| Устройство для реализации двухмерного быстрого преобразования Фурье | 1982 |
|
SU1164730A1 |
| ТРЕНАЖЕР МНЕМОСХЕМ | 1990 |
|
RU2101772C1 |


Авторы
Даты
1981-03-15—Публикация
1978-11-20—Подача