где/д. - длина штанг по оси крена;
/д. - длина штанг по оси рыскания;
тПд., Шг - концевые массы соответственно на штангах 1 и
1/.;
Ф - истинная аномалия; 0 - угол тангажа;
Л , S, С - моменты инерции аппарата без гравитационных штанг;
АО, BO, Со - моменты инерции апнарата со штангамн при
(8) - функция режима работы; е - эксцентриситет орбиты.
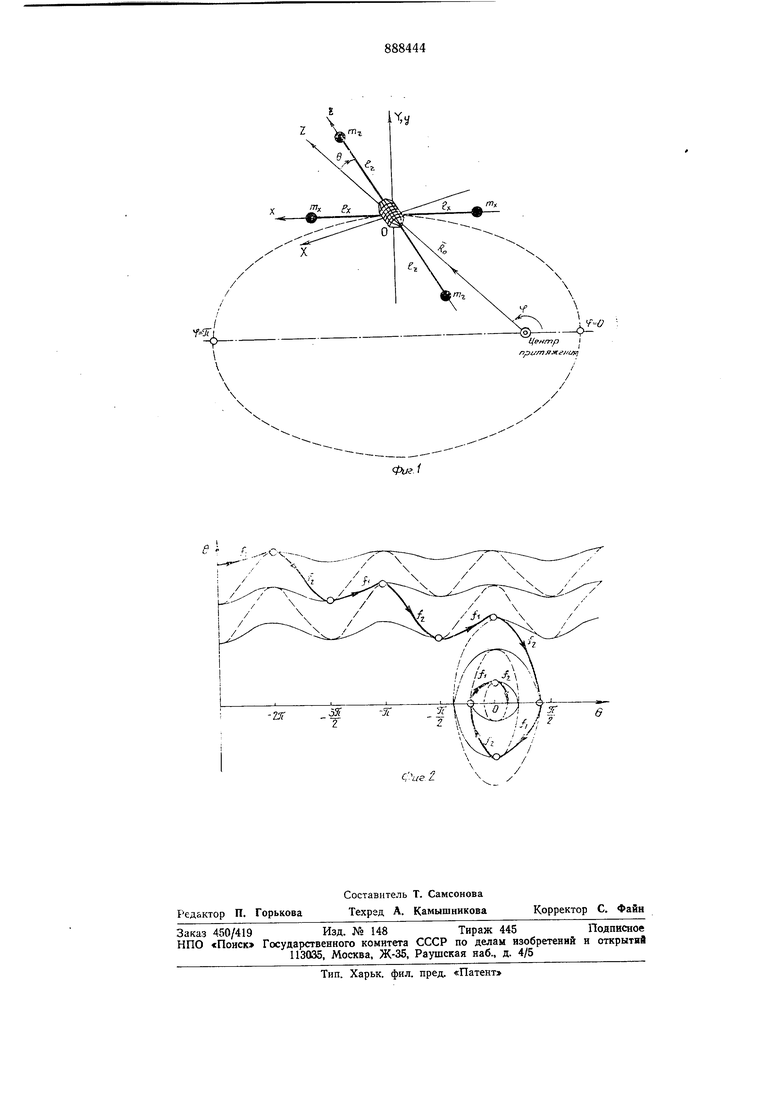
На фиг. 1 изображена система координат и расположение гравитационных штанг; на фиг. 2 - фазовые траектории в плоскости (9, 6).
Базовая система координат XYZ (фиг. 1) связана с орбитой. Начало координат совпадает с центром масс космического аппарата. Оси направлены следующим образом:
-v
OZ - вдоль радиуса-вектора о (по местной вертикали);
ОХ - в плоскости орбиты в сторону движения космического аппарата;
ОУ - перпендикулярно плоскости орбиты.
Систе.ма координат х, у, z связана с космическим аппаратом. Начала координат обеих систем совпадают, а оси х, у, z на9(1 - е cos -f) + (штрихами обозначены производные по ф). Если моменты инерции не регулируются (А, В, С const), члены с В исчезают, н уравнение (3) оказывается неоднородным. Член (-2е sin ф) представляет собой силу, которая вызывает эксцентриситетные колебания. Видно, что в отличие от круговой орбиты, ориентация по местной вертикали не соответствует положению равновесия, т. к. 6 О, и не является решением уравнения (3) при В 0. Если специальным образом в зависимости от ф изменять В, то при условии ( + е cos ®) - 2е sin О, сила, вызывающая эксцентриситетные колебания, компенсируется, и уравнение (3)
правлены вдоль главных осей инерции космического аппарата. Рассматриваются отклонения только в плоскости орбиты (оси у и У совпадают), т. е. их можно характеризовать одним углом в меяаду осями z и Z (именно эти колебания возбуждаются за счет эксцентриситета орбиты). Положение на орбите задают углом ф (истинная аномалия),
А, В, С обозначены главные центральные моменты инерции по осям х, у, z. Их представляют в следующем виде:
А 2.//т„
.S S + 2(/,2m, + /;-X),(1)
С С +2//т,,..
Здесь А, В, С - нере1гулируемая часть А, В, С.
Изменения А, В, С осуществляют регулировкой длин штанг /ж и /2 с массами гпх и i/Пг на концах.
Плоские колебания описывают одним из уравнений Эйлера, которое с учетом
обычных приближений имеет вид
d ,„ .„ .,,. .sin в cos е
(g) - Зш-(Л - С), , , (2)
1 -Ь е cos ci
di
de
где q л +
угловая ско0)
d/ d
рость орбитального движения (для круговой орбиты со const, для эллиптической зависит от ф), е - эксцентриситет орбиты. Выбирают в качестве независимой переменной истинную аномалию ф. Тогда уравнение (2) приобретет вид
(3) ... 50 55 в 4- (1 - cos -f) - 2е sin ср -f - r,- sin 29 + ID ZD 011 -(1 +gcoscp) -2esincp Ui 0 становится однородным. Необходимый закон изменения B(f) определяют из (4): 5(ср). (1 + СО$ср) где .So const - значение б(ф) при тс Ф 2ГДля реализации условия (5) достаточно иметь одну пару гравитационных штанг, расположенных вдоль оси рыскания. Полагая в (1) 1х о, получают ГНТ / /О.„ -1/2 (51 /.- {2т.) (l+ cosf) J С учетом (5) уравнение (3) становится однородным:
А-С
(1 + е cos .p)sin 20 0. (7)
в + Во Как и в случае круговой орбиты, оно имеет решение 6 0. В этом и заключается сущность предложения (1), которое сводится к изменениям /г по закону (6). Однако полной эквивалентности с плоскими колебаниями на круговой орбите в известном способе не достигается, так как периодический множитель (1-|-есо5ф)--он обращается в 1 на круговой орбите - может привести к неустойчивости требуемой ориентации при некоторых значениях е. Можно добиться полной эквивалентности с круговой орбитой, если наряду с изменениями В ((р) по (5), изменять еще Л и С так, чтобы скомпенсировать множитель (И-есо5ф) в (7). Для этого требуется выполнить второе условие: (Л, .()4 (1 -г e 5., - (Л,,-С,;) U) - « (1 -|- ес
Легко убедиться, что при регулировке длин штанг по законам (10), (11) уравнение (7) переходит в
„ 3 0, (12)
ZOff
т. е. имеет место полная эквивалентность условий ориентации по местной вертикали на эллиптической и круговой орбитах. В частности, ориентация по местной вертикали (в 0) будет соответствовать устойчивому положению равновесия. Сам по себе факт эквивалентности уже является полезным, так как позволяет использовать g„-(л„-Co)(l + Ur, в) ( 1 -г е CO 5„ ;-(Л„-Со)(1+ i.(-, и) - - mj (1 -:- е C.O (I (J / (0) sin 2В :зг 0. (15) 2 Соответствующим выбором /(Э) достигают демпфирование колебаний. Для иллюстрации рассматривается пример скачкооб- 40 разных изменений /(в) от /i к /2 и обратно в определенных точках в процессе демпфирования, рассматривая фазовые траектории вг. Такой выбор /(в) позволяет проанилизировать на плоскости (в, 0). Одна- 45 ко скорость выдвижения штанг в известных системах гравитационной стабилизации столь высока, что врем,я существенного изменения 1х, Iz можно считать малым
/-. 0 -О
(8)
1 + е cos W Q
на эллиптических орбитах без изменений все те системы стабилизации космического аппарата, которые разработаны для круговых орбит.
Можно, однако, несколько усложнив законы регулировки длин штанг (10) и (И), обеспечить демпфирование колебаний без каких-либо дополнительных устройств. Для ЭТОГО В (10) и (11) регулируют разность констант Ад-Со в зависимости от в, как это будет показано ниже. При замене в (10) и (11) (Ло-Со) на (Ло-Со) /(в), получают вместо (10), (11), (12): 35 где А((р)-С(ф) при ф Для того чтобы реализовать (5) и (8) одновременно, необходимо наряду со штангами переменной длины / ввести в систему еще одну пару регулируемых штанг 1х, располол енных по оси крена. Законы изменения 1х и /г определяют согласованно из системы двух уравнений: В- - 2.{(,т, + - г:с-|со р (9) л - С -г 2-(/.2m,. - Г.2те,) : . V - г л .f/I +е COS -р Решение системы (9) таково: .cos.) „(д..)| )г cos а) ;- ( ) ) gcos)/(e) + (Л - В - С) о)2 ес089)/(в) )j , (Л ср) по сравнению с периодом колебаний аппарата (это подтверждается ниже численным примером). Поэтому скачкообразное изменение /(в)- является приемлемой аппроксимацией. При f fk const фазовые траектории, соответствующие (15), описываются уравнением eHfi /hSin e h (Q2 3 V. Л const). (16) DO Поскольку /fe может принимать два значения: /iH fz, на фиг. 2 изображены две серии фазовых траекторий. Тонкая сплошная линия соответствует /,, пунктирная - /2 (считают для опреде енности /)/). Параметром для каждой серии является, как обычно, величина h, характеризующая энергию колебаний. При скачкообразных изменениях / на величину б/ значение в в момент «переключения остается непрерывным, следовательно, в соответствии с (16) меняется h: й/г 02з1п2в;- 6/. Рассматривается сначала вращения, когда 6 может принимать любое зиачение. Пусть изменяется f от fz к f в точках в; (2п+1)-, (п - целое число). При этом всякий раз 6/г Q2 (/,-/2)0.. Обратные изменения от /i к /2 необходимо производить в точках вг 2«я (п - целое). В этом случае й/г 0. В целом за иериод т произойдет изменение /г на -2Q2 (/2-/i), чему соответствует Зменьшение максимальной угловой скорости вращения ,) (Индекс О указывает на начало, а т - конец периода изменений в). Уменьшение скорости вращения иллюстрируется фиг. 2, где яркой линией выделена фазовая траектория с учетом «переключений fi7-/2. В режиме колебаний переходы осуществляют при максимальных отклонениях от положения равновесия, когда JO вшах. Так как при этом в О, из (16) получают следующее соотнощение: (h - новое значение h после изменения /). Обратные переходы осуществляют при 8 0, что согласно (16) оставляет h неизменным. Полное изменение ft за один период колебаний определяется по формуле Далее с учетом (16) получают ,, Для малых колебаний скорость демпфирования определяют простым соотнощением
А
f2
л(-)
А
т макс
Р)
/3 макс Данный способ позволяет ориентировать космический аппарат не только по местной вертикали, но и в любом направлении во по тангажу. Для этого достаточно выбрать /в виде / sin2 (в-во). Закон (21) взят в качестве примера для иллюстрации указанной возможности. При выборе /(в) необходимо, чтобы функция /(в) О при в во, была бы положительной при и отрицательной при . Рассматривают малые отклонения от во. Пусть т( В-во, J . После подставки (21) и (15) и линеаризации по г|) получают i|) + О, где Q оуз1п20„. Уравнение (22) показывает, что система совершает колебания с частотой Q в окрестности г)) О (в во). При во, близких к О илипериод колеоании очень сильно возрастает, и способ ориентации становится неэффективным. Однако эти направления также легко стабилизируются. Для во О, как было показано выше, вообще ие требуется дополнительных изменений, т. е. / 1, а для во - s достаточно выбрать / соз2в.(23) При этом (15) переходит в e +-| sin4e Отсюда вытекает, что значения в О, 3it -jr- соответствуют устойчивым положеQ- JL IJ-ииям равновесия, а 4 4 4 4 неустойчивым. Все, что было указано выше о демпфировании колебаний вблизи местной вертикали, полностью верно и для демпфирования колебаний в окрестности в во. В этом легко убедиться, если вместо (21) положить / /feSin2 (в-во), где fh const, которая может принимать два значения /i или fz с «переключениями в точках, где ф | макс и -ф 0. Подобно (20) получают т. е. при произойдет демпфирование колебаний. Для разбора численного при мера осуществления данного способа вы бирают некоторые конкретные данные спутника и орбиты. Рассматривают спутник с моментами ииерции (без гравитационных штанг) Л В 50 кг -м С 30 кг м2 на эллиптической орбите с эксцентриситетом е 0,7. При /д;„акс макс 50 М, m.t mz m 3 кГ скорость выдвижения штанг 0,5 м/с, точность фиксации длины 1х, 2 около 1 см. Определяют, в каких пределах надо изменять 4 и /г, чтобы достичь эквивалентных с круговой орбитой условий ориентации по местной вертикали. Согласно (10) (11) имеют в характерных точках орбиты (ф 0. ; л): 4(0) 0,17 Во-1,7 (Ло-Со)-86,7 1/2 м, 1.( 0,289 Во-() м. 4 (я) 0,96 Во-0,3 (Ло-Со)-2, (25) 4(0) 0,17 Во+1,7 (Ло-Со) -202, м. /J - 0,289 Во+ (Ло-Со) м, /Ля) 0,96 Во + 0,3(Ло-Со)-6,. .Для выбора двух свободных параметров BO и Ло-Со сформулированы два дополнительных условия: - частоты колебаний в(ф) вблизи положения равновесия на круговой и эллиптической орбитах с одинаковым периодом обращения должны быть одинаковыми: л сл .Г1 ДtvQf 0,4 Во в - максимальная длина штанги должна превышать 50 м: /z(jt) 50 м (из указанных в (25) шести значений /ж, 1г /г(я) является максимальным). С учетом (25), (27) находят из (25:): /,,(0) 4,54 м, /J-; 11,09 м I /.х(я) 45,05 м, /,(0) 10,76 м, . () 16,94 м, /Лд) 50 м. По формулам (1) при ф - определяют Ло 1772 кг м2, Во 2510 кг м. Со 768 Ег м. Для дальнейших оценок, кро. ме эксцентриситета, необходимо иметь частоту обращения спутника на орбите. Пусть минимальная высота равна 400 км. Тогда большая полуось а 22,59 т км, а период обращения Т 33,77 10 с , 9,381 ч. 4iacTOTa обращения (о юо (l+i 45,97 X Ч-есозф)2 изменяется от ДО Шмакс 14,76- 10- С-. (соо 5,108 10- с-). Отсюда следует, что необходимое время изменений /х(ф) в /г(ф) по законам (10), (И) измеряют часами и соответствующие регулировки могут быть легко осуществлены. Определяют, в каких пределах необходимо изменять 4, /Z, чтобы осуществить достаточно эффективное демпфирование. Рассматривают малые колебания при условии, чтобы максимальное отклонение от равновесной ориентации уменьшалось за период колебаний, например, в два раза. Согласно (20) для этого необходимо 1 0,5. Ранее было принята иметь Л о Со 0,4. Если теперь выбрать новое б7 Л о С(| 0,2, то это значит, что значение /1 - С -. - и,о. т. Характерные значения длины штанг к Ло - Со « с 0,2 такомоментов инерции для вы: /.-с(О) 6,67 м, /., 12,73 м, 4(я) 46,19 м; /,(0) 9,46 м, /J-J) 15,52 м, /г(я) 50 м; (29) Ло 1495 кг м2, Во 2467 кг м2. Со 1002 кг м. Сравнивают (28) и (29) и определяют, что в какой бы точке орбиты не происхоило демпфирование колебаний, /д;, / неободимо менять в пределах 1-2 м, т. е. на то потребуется несколько секунд. Это ремя должно составлять малую часть ериода колебаний т, т. к. формула (20) праведлива для «мгновенного переключения . Оценим величину т. Безразмерные частоты колебаний в(ф) авны: -О Q, 0,775 при Qa 1,095 при оответствующие периоды в реальном вре2тгени оценивают цо формуле т Наименьшее значение т/тш 3600 с 1,05 ч, следовательно, упрощенное рас11
смотрение с «мгновенным переключением является вполне допустимым.
Характерные масштабы изменений 1х и /г сохраняются и при ориентации в направлении в Поэтому этот случай не рассматривают.
Положительный эффект при ориентации космического аппарата при использовании данного способа состоит в том, что может быть осуществлена ориентация аппарата на эллиптической орбите под любым углом тангажа (в частом случае по местной вертикали); ориентация космического аппарата вдоль избранного направления соответствует устойчивому положению равновесия при любых эксцентриситетах орбиты; может быть осуществлено демпфирование колебаний относительно направления ориентации; для ориентации аппарата не требуются газореактивные двигатели или быстровращающиеся маховикИ; которые имеют малый ресурс рабоL - B -(A.)f(Ql ,
9 - IП4- гпчтЧТГ (Л В - С-)
(1 + ecos ш)2
L -Co)(l+gc
„, -1/2 po + (Ao-Co)(l+gcos)f(e) 2 IП j- /рглсго а
(1 -f f)
l - длина штанг по оси крена;
4 - длина штанг по оси рыскани1я;
т., т - концевые массы соответственно на штангах / и / 30
1,2
Ф - истинная аномалия; в - угол тангажа;
В, С - моменты инерции аппара- 35 та без гравитационных штанг;
12
ты и потребляют значительное количество электроэнергии. Хорошо разработанные конструкции гравитационных штанг регулируемой длины могут быть использованы практически без изменений.
Формула изобретения I
Способ гравитационной ориентации космического аппарата, движущегося по эллиптической орбите, включающий изменение длины ориентированных по оси рыскания гравитационных штанг, отличающийся тем, что, с целью повышения точности ориентации путем обеспечения устойчивой ориентации с заданным углом тангажа и одновременного демпфирования колебаний космического аппарата, изменяют длину гравитационных штанг, ориентированных по оси крена, причем длины штанг изменяют по зависимостям:
1/2
. (Л + 5 c«)
АО, BO, CQ - моменты инерции аппарата со штангами при/(в) - функция режима работы; е - эксцентриситет орбиты.
Источник информации, принятый во внимание при экспертизе:
1. Г. М. Коннел. Метод управления пространственным положением спутника с ориентацией на Землю для эллиптических орбит. - «Ракетная техника и космонавтика, 10, № 3, 1972, с. 24-32.
Ху





| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОДНООСНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА ВЫТЯНУТОЙ ФОРМЫ | 2010 |
|
RU2457159C2 |
| СПОСОБ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО АППАРАТА С НЕПОДВИЖНЫМИ ПАНЕЛЯМИ СОЛНЕЧНЫХ БАТАРЕЙ ПРИ ВЫПОЛНЕНИИ ЭКСПЕРИМЕНТОВ НА ОРБИТАХ С МАКСИМАЛЬНОЙ ДЛИТЕЛЬНОСТЬЮ ТЕНЕВОГО УЧАСТКА | 2010 |
|
RU2457158C2 |
| СПОСОБ ПОЛУПАССИВНОЙ ТРЕХОСНОЙ СТАБИЛИЗАЦИИ ДИНАМИЧЕСКИ СИММЕТРИЧНОГО ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ | 2006 |
|
RU2332334C1 |
| СПОСОБ МОНИТОРИНГОВОЙ КОЛЛОКАЦИИ НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2013 |
|
RU2558959C2 |
| СПОСОБ ОДНООСНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА ВЫТЯНУТОЙ ФОРМЫ | 2015 |
|
RU2594056C1 |
| СПОСОБ РАЗВЕРТЫВАНИЯ И ЗАКРУТКИ ОТНОСИТЕЛЬНО ЦЕНТРА МАСС КОСМИЧЕСКОЙ ТРОСОВОЙ СИСТЕМЫ С ПОМОЩЬЮ ГРАВИТАЦИОННЫХ И ВНУТРЕННИХ СИЛ | 2012 |
|
RU2536611C2 |
| СПОСОБ ИЗМЕРЕНИЯ АНОМАЛИЙ ГРАВИТАЦИОННОГО ПОЛЯ ЗЕМЛИ ПРИ ПРОВЕДЕНИИ ЛАБОРАТОРНЫХ РАБОТ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2008 |
|
RU2398249C2 |
| СПОСОБ УДЕРЖАНИЯ КОСМИЧЕСКОГО АППАРАТА НА ГЕОСИНХРОННОЙ 24-ЧАСОВОЙ ОРБИТЕ | 2013 |
|
RU2535353C2 |
| СПОСОБ ОДНООСНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА ВЫТЯНУТОЙ ФОРМЫ | 2015 |
|
RU2594057C1 |
| СПОСОБ ТРЕХОСНОЙ ГРАВИТАЦИОННОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА НА ОРБИТЕ СПУТНИКА ЗЕМЛИ | 1995 |
|
RU2128607C1 |


Авторы
Даты
1982-05-07—Публикация
1979-11-13—Подача